21.3 分割表のカイ二乗分析
分割表の χ2 分析を使うのは:
- 2つ以上の異なるクラスやカテゴリに個体が分類される2つ以上の群の分布を比較したいとき。
- 2 x 2 分割表のそれぞれのセルに期待できる観測値が5つ以上あるとき。
2 x 2 分割表のセルのいずれかに観測値が5つより少ないものがある場合は、フィッシャーの直接法を使います。詳しくは、フィッシャーの直接法 (Fisher Exact Test) をご覧ください。χ2 検定の計算は、行と列が独立であることが前提条件になります。行と列に依存関係がある場合、すなわち、同一の群が連続する2つの処理を受ける場合は、マクニマーの検定を使います。詳しくは、マクニマーの検定 (McNemar’s Test) をご覧ください。
1. カイ二乗検定について
カイ二乗検定で分析するのは分割表 (contingency table) のデータです。分割表とは、それぞれの群の個体数がカテゴリごとに分類されたテーブルです。特性やカテゴリの違いが表の列に、群の違いが表の行 (またはその反対) になります。カテゴリと群を組み合わせであるテーブルの各セルには個体数がリストされます。
例えば、2 x 2 分割表では2つの群と2つのカテゴリ (2つの行と2つの列) があり、2 x 3 分割表では、2つの群と3つのカテゴリ、あるいは、3つの群と2つのカテゴリがあるという具合になります。
| Species | Location | ||
|---|---|---|---|
| Tundra (ツンドラ) |
Foothills (山ろく地帯) |
Treeline (高木限界線) |
|
| Lowland (スコットランド) |
125 | 16 | 6 |
| Alpine (アルプス) |
7 | 19 | 117 |
χ2 検定では、各セルの行の合計と列の合計の百分率をそれぞれ使用して、処理効果がないかセル毎に期待される観測数を計算します。χ2 統計量は、期待度数と観測度数の間の差を要約します。
2. カイ二乗検定を実行する
カイ二乗検定 (Chi-Square Test) を実行するには:
- ワークシートに適切なデータを入力または配置します。詳しくは、カイ二乗検定のデータを配置するをご覧ください。
- 必要があれば、Chi-Square オプションを設定します。
- Analysis タブをクリックします。
- SigmaStat グループにある Tests ドロップダウンリストから以下を選択します:Rates and Proportions → Chi-Square
- 検定を実行します。
- Chi-Square レポートを表示して解釈します。詳しくは、分割表のカイ二乗分析の結果を解釈するをご覧ください。
3. カイ二乗検定のデータを配置する
ワークシートに配置できるデータは、分割表形式のデータまたはインデックス付きの生データ形式のいずれかです。
- Tabulated Data :表形式のデータは、観測数を分割表の各セルに配置してあらわしたものです。ワークシートの行と列は、それぞれ群とカテゴリに対応します。観測数は整数である必要があります。なお、群とカテゴリに対応する行列の並びと配置は、重要ではない点に注意してください。カテゴリに行を、群に列を使っても、その逆を使ってもかまいません。
| Species | Location | ||
|---|---|---|---|
| Tundra | Foothills | Treeline | |
| Lowland | 125 | 16 | 6 |
| Alpine | 7 | 19 | 117 |
- Raw Data:ワークシートの1つの列に群を、もう一つの列に対応するカテゴリを配置することによって個々の観測データの群とカテゴリをレポートすることができます。それぞれの行は1つの観測データに対応するので、データの行数は観測データの総数と同じだけあることになります。SigmaPlot はこれらのデータがら自動的にクロス表を作成し、できあがった分割表に対して χ2 分析を実行します。
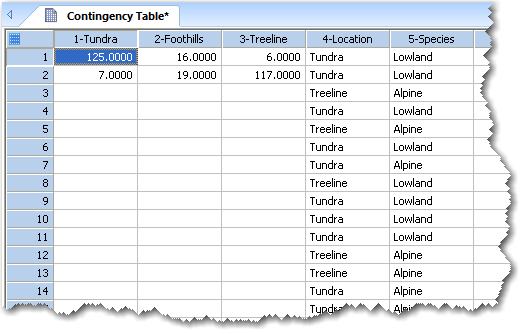
上記ワークシートの列1から3までが表形式、列4と5が生データになります。
4. カイ二乗オプションを設定する
カイ二乗オプションを使用するのは:
- カイ二乗検定で実行する検定の検出力 (Power) をレポートに表示する場合
- イェーツの補正因子 (Yates Correction Factor) を有効にする場合
カイ二乗オプションを変更するには:
- 検定オプションの変更後に検定を実行するに際して、検定の実行前にデータを選択しておきたい場合は、対象とするデータ列をポインターでドラッグしておきます。
- Analysis タブの SigmaStat グループにある Select Test ドロップダウンリストから Chi-square を選択します。Options for Chi-Square ダイアログボックスが表示されます。
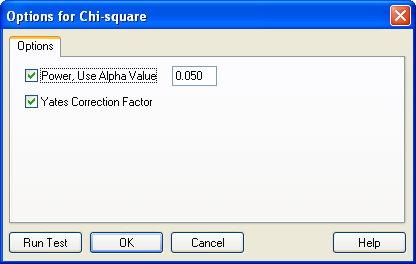
Options for Chi-Square ダイアログボックス - 検定オプションを有効または無効するにはチェックボックスをクリックします。SigmaPlot を次回以降起動するときは、ここで選択したオプションの内容が全て保持されます。
- 検定を続行するには、Run Test をクリックします。
- 現在の設定内容を適用して、オプションダイアログを閉じるには、OK をクリックします。
7.3.4.1 Options for Chi Square
- Power, Use Alpha Value:選択すると検定の感度を検出します。検出力、すなわち、検定の感度は、2群の割合の間に真の差があるとすれば、この検定でそれを検出できる確率です。アルファの値を変更するには、Alpha Value ボックスの数値を編集します。アルファ (α) は、誤って差があると判断しても良しとする確率です。SigmaPlot で提示される値は、α = 0.05 です。この設定は、誤りを許容する確率が 20分の1であることを示します。すなわち、P < 0.05 であれば有意な差があると判断できることになります。α 値を小さくすると、有意差があると結論付ける要件がそれだけ厳格なものになりますが、差があるにもかかわらずないと結論付けてしまう可能性はそれだけ大きくなります。α 値を大きくすると、差があると結論付ける要件はそれだけ容易になりますが、誤判定をレポートしてしまうリスクが増加することになります。
- Yates Correction Factor:統計的検定に2 x 2 分割表の分析や、マクニマーの検定 (McNemar’s test) など自由度1の χ2 分布を使用する場合、算出される χ2 は、χ2 検定統計量の実際の分布と比較すると P 値が非常に小さくなる傾向があります。理論上の χ2 分布は連続的ですが、この χ2 検定統計量の分布は離散的であるからです。計算される χ2 の値を下げてこの食い違いを補うように調整するには、イェーツの連続補正 (Yates Continuity Correction) を使います。イェーツの補正を使うことで、検定を保守的なもの、例えば、P 値が大きくすることで誤判定の結論を下す可能性を低く抑えることができます。イェーツの補正は、2 x 2 分割表や自由度1の χ2 分布を元に P 値を算出するその他の統計で適用します。Yates Correction Factor のチェックボックスをクリックすることで、この設定を有効または無効にすることができます。
5. カイ二乗検定を実行する
検定を実行するには、検定するデータを選択する必要があります。検定ウィザードの Select Data パネルを使用して、検定したいデータを含むワークシートの列を選択したり、お持ちのデータがどのような状態でワークシートに配置されているかを指定します。
カイ二乗検定を実行するには:
- 検定の実行前にデータを選択しておきたい場合は、対象とするデータ列をポインターでドラッグしておきます。
- Analysis タブをクリックします。
- SigmaStat グループにある Tests ドロップダウンリストから次を選択します:Rates and Proportions → Chi-SquareChi-Square — Data Format ダイアログボックスが表示され、データフォーマットを選択するよう指示されます。
- Data Format ドロップダウンリストから適切なデータフォーマットを選択します。分割表のデータを検定する場合は、Tabulated を選択します。お持ちのデータが生データの形式で配置されている場合は Raw を選択します。詳しくは、カイ二乗検定のデータを配置するをご覧ください。
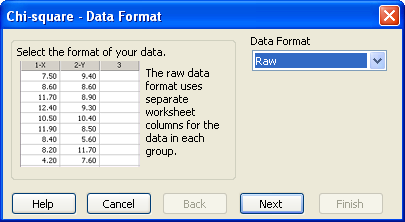
データフォーマットの選択を指示する Chi-Square — Data Format ダイアログ - Next をクリックして検定に使用するデータ列を選択します。検定を選択する前に列を選択していれば、選択された列が selected columns リストに表示されます。列をまだ選択していない場合は、データを選択するようダイアログボックスで指示されます。
- Selected Columns リストに別のワークシート列を割り当てたい場合には、ワークシートで直接その列を選択するか、Data for Observations または Data for Category ドロップダウンリストからその列を選択します。最初に選択した列は、Selected Columns リストの Observation または Category 行に割り当てられ、二番目以降の列は それぞれ次の行に割り当てられます。各行には、選択した列のタイトルが表示されます。生データの場合、ワークシートの列を2つ選択するよう指示されます。表形式のデータの場合は、64 列を上限とする列を選択するよう指示されます。
- 選択した内容を変更するには、リストの割り当てを選択したあと、ワークシートから列を選択しなおします。Selected Columns リストの内容をダブルクリックすることによって、列の割り当てを消去することもできます。
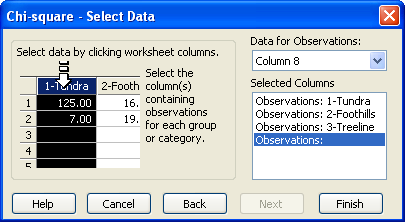
データ列を選択するよう指示する Chi-Square — Select Dataダイアログボックス - Finish をクリックすると、検定が実行されます。期待値が5よりも小さいセルが分割表に多くある場合、SigmaPlot は以下のいずれかをおこないます:分割表の群やカテゴリを見直して、セル数を減らしたり、1セルあたりの観測数を増やすように提案します。テーブルが 2 x 2 分割表の場合は、フィッシャーの直接法が提案されます。期待される観測数が5以下のセルが多数ある場合、理論的な χ2 分布では実際の χ2 検定統計量を正確にあらわされないので、算出される P 値に精度を期待できません。フィッシャーの直接法 (Fisher Exact Test) では、観測した特定の 2 x 2 分割表の両側確率を正確に計算しますので、全てのセルの期待度数が5を上回る必要はありません。この検定が完了すると、 χ2 検定のレポートが表示されます。詳しくは、分割表のカイ二乗分析の結果を解釈するをご覧ください。
6. 分割表のカイ二乗分析の結果を解釈する
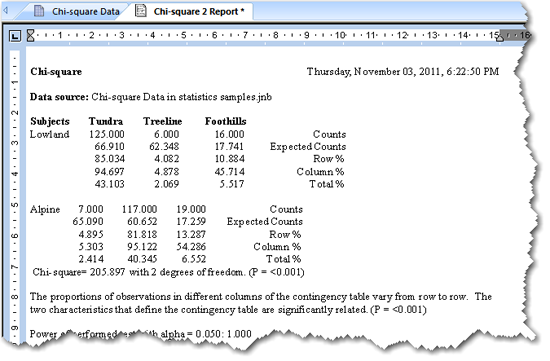
χ2 検定のレポートには、分割表データのサマリー、その分布を元に算出された χ2 統計量、および、χ2 の P 値が一覧で表示されます。
結果の説明
数値による結果に加えて、拡張された結果の説明が表示されることがあります。この説明テキストは、Options ダイアログボックスで有効または無効にすることができます。また、表示する小数点以下の桁数についても Options ダイアログボックスで設定できます。
6.1 分割表のサマリー
テーブルのセル毎に各種統計量があらわされます。
- Observed Counts:分割表のデータを元に得られた1セルあたりの観測数です。
- Expected Frequencies:行と列の百分率を使って予測された分割表の各セルの期待度数です。
- Row Percentage:各セルの観測度数をその行の全観測度数で割って求めた分割表の各行の観測度数に占める百分率です。
- Column Percentage:各セルの観測度数をその列の全観測度数で割って求めた分割表の各列の観測度数に占める百分率です。
- Total Cell Percentage:各セルの観測度数を表の全観測度数で割って求めた分割表の観測度数全体に占める百分率です。
6.2 カイ二乗
テーブルの各セルの観測度数と期待度数の差の二乗を合計したもので、次式であらわされます。
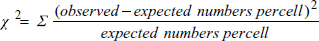
この計算では、行と列が互いに独立であることが仮定されます。
もし、 χ2 の値が大きいものであれば、分布に差がある (例えば、期待度数と観測度数の間に行と列が独立であることを示す大きな差がある) と結論付けることができます。
χ2 の値がゼロ付近であれば、分割表のパターンが無作為な度数の分布であるときに期待されるものと差がないことを示します。
- Yates Correction:イェーツの補正を使って χ2 を補正します。これによって、2 x 2 分割表の P 値が実際の χ2 分布を反映するように精度を高めます。イェーツの補正を有効にするには、Options for Chi-Square ダイアログボックスで指定しますが、適用できるのは 2 x 2 分割表のみとなります。
- P Value:P 値は、観測数の分布に真の差があると誤って結論付けてしまう確率です (例えば、χ2 に基づいて帰無仮説を誤って棄却する、すなわち第一種の誤り (Type I error) を犯す確率)。 P 値が小さいほど、標本がカテゴリ間に異なる分布をもつ母集団から抽出される確率は高くなります。伝統的には、P < 0.05 であれば、有意差があると結論付けることができます。
6.3 検出力 (Power)
カイ二乗検定の検出力 (Power)、すなわち感度は、群間に真の差がある場合、その検定で群間の差を検出できる確率です。検出力が 1 に近づくほど、その検定の感度は高くなります。カイ二乗の検出力は、サンプルサイズと測定された各標本の割合によって影響を受けます。この結果は、Options for Chi-Square ダイアログボックスで無効にしない限り表示されます。
- アルファ:アルファ (α) は、誤って差があると結論付けすることが許容される確率です。この誤りを、第一種の誤り (Type I error) と呼ぶこともあります (第一種の誤りは、効果がないという帰無仮説が真であるにもかかわらずそれを棄却するときです)。α 値は、Power Option ダイアログボックスで設定します。提示される α = 0.05 という値は、許容する誤りを 20分の1にすることを示します。α の値を小さくするほど、有意差があるとの結論に至る要件はそれだけ厳格になりますが、その反面、差があるにもかかわらず差がないと結論付けてしまう可能性は高くなります (第二種の誤り:Type II error)。α の値を大きくすれば、差があるという結論付けは容易になりますが、その反面、誤った差をレポートするリスクが高まります (第一種の誤り:Type I error)。
