23.3 多重線形回帰

多重線形回帰 (Multiple Linear Regression) を使うのは：

平面 (または超平面) をデータに当てはめることによって、ある変数の値をそれ以外の複数の変数の値から予測するとき。
独立変数が複数あることが既知であり、それらを使ってモデルを求めたいとき。

独立変数は、予測変数とも呼ばれる既知の変数です。独立変数を変化させると、それに対応する従属変数 (応答変数ともいう) の値が決まります。

独立変数が１つしかないことが既知である場合は、単純線形回帰 (Simple Linear Regression) を使います。全ての独立変数をモデルに使用すべきかどうかが分からない場合は、段階的 (Stepwise) またはベストサブセット (Best Subsets) 回帰を使って選択した独立変数の候補の中から重要な独立変数を特定します。

関係が直線や平面でない場合は、多項式 (Polynomial) や非線形 (Nonlinear) 回帰を使うか、変数変換を使います。

多重線形回帰について
多重線形回帰を実行する
多重線形回帰のデータを配置する
多重線形回帰オプションを設定する
多重線形回帰を実行する
多重線形回帰の結果を解釈する
多重線形回帰のレポートグラフ
1. 多重線形回帰のレポートグラフを作成する

1. 多重線形回帰について

多重線形回帰 (Multiple Linear Regression) では、従属変数と k 個の独立変数との関係性が以下の多次元平面の一般方程式で当てはめられることが仮定されます：

y =b₀+b₁x₁+b₂x₂+b₃x₃+…b_kx_k

ここで、y は従属変数、x₁, x₂, x₃, …, x_k は k 個の独立変数、そして、b₁, b₂, b₃, …, b_k は k 個の回帰係数です。

x_i の値を変化させると、それに対応する回帰係数 b_i の符号に応じて、y の値も増加または減少します。

多重線形回帰では、選択した全ての独立変数を使って実際のデータを最も良く説明する k+1 次元の平面を求めます。

多重線形回帰は、パラメトリック検定です。すなわち、独立変数の値の集合が与えられると、その従属変数がとり得る値は回帰平面について正規分布に従い分散が等しいものと仮定されます。

2. 多重線形回帰を実行する

多重線形回帰を実行するには：

ワークシートに適切なデータを入力または配置します。詳しくは、多重線形回帰のデータを配置するをご覧ください。
レポートグラフを作成します。詳しくは、多重線形回帰のレポートグラフをご覧ください。

3. 多重線形回帰のデータを配置する

測定された従属変数のデータを１列に、それに対応する独立変数のデータを２列目以降の列に配置します。

4. 多重線形回帰オプションを設定する

多重線形回帰オプションを使うのは：

前提条件のチェックオプションを設定するとき。
残差の表示とワークシートへの保存を設定するとき。
信頼区間の表示とワークシートへの保存を設定するとき。
PRESS 予測誤差と標準化回帰係数を表示するとき。
外れ値や影響力のあるデータポイントを識別するための検定を指定するとき。
VIF (variance inflation factor) を設定するとき。
検出力 (Power) を表示するとき。

多重線形回帰オプションを変更するには：

検定オプションの変更後に検定を実行するに際して、検定の実行前にデータを選択しておきたい場合は、対象とするデータ列をポインターでドラッグしておきます。
Analysis タブを選択します。
SigmaStat グループの Tests ドロップダウンリストから Multiple Linear Regression を選択します。
Options をクリックします。Options for Multiple Linear Regression ダイアログボックスに以下の４つのタブが表示されます：
1. Assumption Checking：Assumption Checking タブをクリックすると、Normality (正規性)、Constant Variance (等分散性)、および Durbin-Watson オプションが表示されます。詳しくは、Options for Multiple Linear Regression: Assumption Checking をご覧ください。
2. Residuals：Residuals タブをクリックすると、残差オプションが表示されます。詳しくは、Options for Multiple Linear Regression: Residuals をご覧ください。
3. More Statistics：More Statistics タブをクリックすると、信頼区間、PRESS 予測誤差、および、標準化係数オプションが表示されます。詳しくは、Options for Multiple Linear Regression: More Statistics をご覧ください。
4. Other Diagnostics：Other Diagnostics タブをクリックすると、Influence (影響力) 、Variance Inflation Factor、および、Power (検出力) のオプションが表示されます。詳しくは、Options for Multiple Linear Regression: Other Diagnostics をご覧ください。
チェックボックスを選択して各検定オプションを有効または無効にします。SigmaPlot を次回以降起動するときは、ここで選択したオプションの内容が保持されます。詳しくは、多重線形回帰の結果を解釈するをご覧ください。
検定を続行するには、Run Test をクリックします。
現在の設定内容を適用して、オプションダイアログを閉じるには、OK をクリックします。

4.1 Options for Multiple Linear Regression: Assumption Checking

プションダイアログボックスから Assumption Checking タブを選択すると、Normality、Constant Variance、および、Durbin-Watson オプションが表示されます。これらのオプションは、お持ちのデータが回帰分析にふさわしいか否かを、そのデータについて多重線形回帰が行う３つの仮説をチェックすることによって検定するものです。多重線形回帰で仮定するのは：

元の母集団が線形回帰について正規分布していること。
元の母集団の従属変数の分散が独立変数の値とは無関係に一定であること。
残差が互いに独立していること。

デフォルトでは全ての Assumption Checking (前提条件のチェック) オプションが選択されています。これらのオプションは、使用するデータが等分散の正規分布に従っており、その残差が互いに独立であることが確実に分かっているときだけ無効にしてください。

Normality の検定：SigmaPlot では、母集団の分布の正規性検定に Shapiro-Wilk または Kolmogorov-Smirnov のいずれかを使用します。
Constant Variance Testing (等分散性の検定)：SigmaPlot では、等分散性の検定に残差の絶対値と観測された従属変数の値との間のスピアマンの順位相関 (Spearman rank correlation) を計算します。この相関関係が有意であれば等分散性の前提条件は棄却されますので、その場合は、別モデル (例えば、データの形状により密接に従うようなモデル) での試行を検討するか、単一または複数の独立変数の分散安定化の変換を行う必要があります。

P Values for Normality and Constant Variance (正規性と等分散性の P 値)： P 値は、データが正規分布に従っていないと誤って結論付けてしまう確率を決定します (そのデータは正規分布に従っているという帰無仮説を誤って棄却してしまうリスクが P 値です)。ここで設定した P 値よりも、検定で算出された P 値が大きければ検定は採択 (Pass) されます。正規性と等分散のいずれかまたは両方の要件をより厳密なものにするには、この P 値を大きくします。パラメトリックな統計手法では、仮説の棄却が比較的ロバスト (頑健) に検出されることから、SigmaPlot ではこの値を 0.05 としています。P 値をこれよりも大きくすると (例えば、0.10)、そのデータに正規性がないとの判定が出やすくなります。正規性と等分散のいずれか又は両方の要件を緩和するには、P 値を小さくします。正規性があるという仮説を棄却するための P 値に小さい値しか要求しないということは、前提とする正規分布からデータが外れていても、それが非正規であると判定される前に、それだけ広く受け入れたいとする意思があることを意味します。例えば、P 値を 0.050 とした場合、あるデータを非正規であると判定するには、0.100 の場合と比べてそれだけ大きく正規性を逸脱していなければなりません。

※ Tip：この前提条件の検定では、非正規や等分散性でない母集団のデータ検出においてロバストな処理がなされますが、データ分布が極端な条件では検出できない場合があります。しかし、このような条件の場合は、前提条件の自動検定に頼らずにデータを視覚的に調べることで容易に検出することができます。

Durbin-Watson 統計量： SigmaPlot では、残差が互いに独立していることを検定するのに Durbin-Watson 統計量を使用します。Durbin-Watson 統計量は、残差間の系列相関を測定するものです。この残差は、多くの場合、独立変数が時間で、かつ、観測値と回帰直線との間のある時点のずれが、前の時点におけるずれと関連性がある場合に相関します。残差間に相関性がない場合、Durbin-Watson 統計量は 2 になります。
Difference from 2 の値：系列相関の根拠とみなす 2.0 からの許容できるずれを Difference from 2.0 ボックスに入力します。算出される 2.0 からのずれである Durbin-Watson 統計量が入力した値より大きければ、残差に独立性がない可能性があることが SigmaPlot によって警告されます。例えば、このずれの値を提示された値 0.50 にすると、Durbin-Watson 統計量の値が 2.5 より大きいか、1.5 より小さい場合に残差に相関性があるというフラッグが立てられます。独立性の条件を厳しくするには、difference from 2.0 の値を小さくします。独立性の条件を緩和するには、difference from 2.0 の値を大きくします。

4.2 Options for Multiple Linear Regression: Residuals

プションダイアログボックスの Residuals タブを選択すると、Predicted Values, Raw, Standardized, Studentized, Studentized Deleted, および Report Flagged Values Only オプションが表示されます。

Predicted Values (予測値)：このオプションを使用すると、独立変数の観測値ごとに従属変数の予測値が計算され、その結果がワークシートに保存されます。予測値をワークシートに含めたくなければ、選択されたチェックボックスをクリックします。予測値をワークシートの列に配置するには、対応するドロップダウンリストから配置先の列番号を選択します。ドロップダウンリストで none を選択し、Predicted Values チェックボックスが選択されている場合は、レポートにはその値が表示されますが、ワークシートには配置されません。
Raw Residuals (生の残差)：生の残差は、従属変数に関する予測値と観測値の差です。生の残差をレポートに含めるには、このチェックボックスが選択されているかを確認してください。生の残差をワークシートに含めたくなければ、選択されたチェックボックスをクリックします。生の残差をワークシートの列に配置するには、対応するドロップダウンリストから配置先の列番号を選択します。ドロップダウンリストで none を選択し、Raw チェックボックスが選択されている場合は、レポートにはその値が表示されますが、ワークシートには配置されません。
Standardized Residuals (標準化残差)：標準化残差は、残差をその推定量の標準誤差で割ったものです。残差の標準誤差は、要するに残差の標準偏差ですので、回帰直線周辺のばらつきの尺度となります。標準化残差をレポートに含めるには、このチェックボックスが選択されていることを確認してください。標準化残差をワークシートに含めるには、このチェックボックスを選択してください。SigmaPlot は、対応するボックスで指定した信頼区間から外れたデータポイントに対して自動的にフラッグを立てます。例えば、データポイントの中心から外れたデータポイントは、標準化残差の値が「大きい」と判断されます。フラッグを立てるデータポイントは、Flag Values > 編集ボックスの値を編集することで変更することができます。
Studentized Residuals (スチューデント化残差)：スチューデント化残差は、データの両極値に対する中央付近の回帰直線の精度の高さを考慮に入れることによって残差を基準化するものです。スチューデント化残差は、スチューデントの t 分布に従う傾向がありますので、t 分布を利用してスチューデント化残差の大きい値を決定することができます。SigmaPlot は、例えば、データポイントの中心から外れたデータポイントに対しては、スチューデント化残差の値が「大きい」というフラッグを自動的に立てます。フラッグで提示されるデータポイントは、回帰母集団の95％信頼区間の外側にあります。レポートにスチューデント化残差を含めるには、Studentized チェックボックスが選択されていることを確認してください。スチューデント化残差をワークシートに含めたくない場合は、選択されたチェックボックスをクリックしてください。
Studentized Deleted Residuals (スチューデント化削除残差)：スチューデント化削除残差は、スチューデント化残差に似ていますが、該当するデータポイントを使わずに、回帰方程式を計算することで値を求める点が異なります。スチューデント化削除残差をレポートに含めるには、このチェックボックスが選択されているかを確認してください。スチューデント化削除残差をワークシートに含めたくなければ、選択されたチェックボックスをクリックします。SigmaPlot は、例えば、データポイントの中心から外れたデータポイントに対しては、スチューデント化削除残差の値が「大きい」というフラッグを自動的に立てます。フラッグで提示されるデータポイントは、回帰母集団の95％信頼区間の外側にあります。

※ Tip：スチューデント化残差、および、スチューデント化削除残差はいずれも、同じ信頼区間の設定を使って外れ値を判定します。
Report Flagged Values Only (フラッグ値のみレポートする)：レポートにフラッグの立てられた標準、および、スチューデント化削除残差しか含めない場合は、Report Flagged Values Only を選択してください。このオプションを解除すると、標準化残差およびスチューデント化残差のすべてがレポートに含まれます。

4.3 Options for Multiple Linear Regression: More Statistics

オプションダイアログの More Statistics タブをクリックすると、信頼区間オプションが表示されます。母集団、回帰、または、両方の信頼区間を設定し、それらをワークシートに保存することができます。

Confidence Interval for the Population：母集団の信頼区間では、観測データを抽出した母集団が含まれる領域を定義する値の範囲を与えます。母集団の信頼区間をレポートに含めるには、Population が選択されているかを確認してください。母集団の信頼区間をレポートに含めたくなければ、このチェックボックスを外します。
Confidence Interval for the Regression：回帰直線の信頼区間は、指定した信頼水準で従属変数と独立変数の間に真の平均値の関係が含まれる領域がこの値の範囲によって定義されます。レポートに回帰の信頼区間を含めるには、Regression チェックボックスが選択されているかを確認し、パーセントボックスに信頼水準の値を入力して指定してください。信頼水準は 1 から 99 までの任意の値にすることができます。提示される区間の信頼水準はいずれも 95 % です。レポートに母集団の信頼区間を含めたくない場合は、選択されたチェックボックスをクリックしてください。
信頼区間をワークシートに保存する。信頼区間をワークシートに保存するには、Starting in Column ドロップダウンリストから区間データを保存したい最初の列の列番号を選択します。ワークシートの指定した列以降に選択した区間データが保存されます。
PRESS Prediction Error (PRESS 予測誤差)：PRESS 予測誤差は、回帰方程式がデータにどれだけ良くあてはまっているかを測る尺度です。このチェックボックスを選択した状態にしておけば、PRESS 統計量を用いて方程式の当てはめが評価されます。レポートに PRESS 統計量を含めたくなければ、選択されているこのチェックボックスを解除します。
Standardized Coefficients (標準化係数)：回帰方程式の係数を無次元の値に標準化したものです。

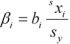
ここで、b₁ = 回帰係数、^sx_i = 独立変数 x_i の標準偏差、そして、 s_y = 従属変数 y の標準偏差です。

レポートに標準化係数を含めるには、Standardized Coefficients を選択します。標準化係数をワークシートに含めたくない場合は、このオプションを解除します。

4.4 Options for Multiple Linear Regression: Other Diagnostics

Options for Multiple Linear Regression ダイアログボックスの Other Diagnostics タブをクリックすると、Influence オプションが表示されます。Influence オプションは、影響力のあるデータポイントのインスタンスを自動的に検出するものです。影響力がもっとも強いポイントは、データポイントの外れ値です。すなわち、それ以外のデータポイントと一直線上に並ぼうとはしないものです。これらの点は、回帰直線の計算において極端に強い影響を及ぼす可能性があります。影響力のあるポイントを識別し定量化するための影響力の検定には、幾つかの種類が用意されています。

DFFITS ：DFFITS_i は、データセットの中から i 番目のデータポイントを除外したときに変化する予測値の標準誤差を見積る数です。あるデータポイントの予測値に対する影響力を測るもうひとつの尺度で、回帰係数を計算するのに使用します。データポイントを除外したとき、その予測値の変化の標準誤差が２以上であれば影響力ありと判断されます。
DFFITS を選択すると、全てのポイントについて DFFITS 値を計算し、影響力のある点、例えば、DFFITS の値が Flag Values > 編集ボックスで指定した値よりも大きい値には、フラッグが立てられます。データの中で影響力が大きい点であることをあらわす標準誤差として提示される値は 2.0 です。影響力のある点として余分なフラッグを立てないようにするには、この値を高くします。影響力のより小さなポイントにフラッグを立てるには、この値を低くします。詳しくは、影響点の対処法をご覧ください。
Leverage：回帰方程式の結果に影響を及ぼすポイントである可能性があるかを識別するには Leverage を選択します。てこ比は、独立変数の値にのみ依存します。てこ比の高い観測データは、独立変数の極値 (大きい値と小さい値) になる傾向があります。このような点では、独立変数のわずかな変化が従属変数の予測値に大きく影響を及ぼす可能性があります。データポイントのてこ比の期待値は次式であらわされます：

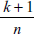
ここで、k は独立変数の数、n はデータポイントの数です。観測データのレバレッジが期待されるレバレッジより大きい場合は、その点に影響力がある疑いがあります。

Leverage を選択すると、ポイント毎のてこ比を計算し、影響力の疑いのある点、例えば、期待されるてこ比が指定した倍数より大きいものであれば自動的にフラッグが付けられます。提示される値は、その回帰に期待されるてこ比の 2.0 倍です。例えば、

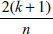
影響力の疑いがある点として余分なフラッグを立てないようにするには、この値を高くします。影響力の小さなポイントにフラッグを立てるには、この値を低くします。詳しくは、影響点の対処法をご覧ください。
Cook’s Distance (クックの距離)：クックの距離は、回帰方程式のパラメータ推定値に対して各ポイントの影響力がいかに大きいかを測る尺度です。クックの距離は、ある点を分析から除外したときに回帰係数の値がどれだけ変化するかを評価します。クックの距離は、独立変数と従属変数の両方の値に依存します。全てのポイントに対してこの値を計算し、影響力のあるポイント、例えば、指定値よりもクックの距離の値が大きいポイントに対してフラッグを立てるようにするには、Cook’s Distance を選択します。提示される値は 4.0 です。クックの距離が 1 より大きければ、その点に影響力が存在する可能性があることを示します。クックの距離が 4 より大きければ、その点はパラメータの推定値に対して大きな影響力があることを示します。影響力のある点として余分なフラッグを立てないようにするには、この値を高くします。影響力の小さなポイントにフラッグを立てるには、この値を低くします。詳しくは、影響点の対処法をご覧ください。
Report Flagged Values Only (フラッグを立てた値のみレポートする) ：影響力ポイント検定でフラッグが立てられた影響力のポイントだけをレポートに含める場合は、Report Flagged Values Only を選択します。このオプションを解除すると影響力のある全てのポイントがレポートに含まれることになります。
Power (検出力) ：回帰の検出力は、観測されたデータの中に関係性を検出する能力です。アルファ (α) は誤って関係ありと判断されることを許容する確率です。線形回帰データの検出力を計算するには、Power を選択します。アルファ値を変更するには、Alpha Value 編集ボックスの数値を編集します。提示される値は α = 0.05 です。この設定は、誤りを許容する確率が 20分の１であることを示します。すなわち、P < 0.05 であれば有意な関係があると判断できることになります。アルファの値を小さくすると、有意な関係があると結論付ける要件がそれだけ厳格なものになりますが、関係があるにもかかわらず関係がないと結論付ける可能性が高くなります。アルファの値を大きくすると、関係があるとの結論付けが容易になりますが、それだけ誤判定をレポートする危険性が高くなります。
Variance Inflation Factor：独立変数の多重共線性 (multicollinearity) を測定するには、Variance Inflation Factor を選択します。回帰プロシージャーでは、独立変数は統計的に互いに独立であることが仮定されます。例えば、ある独立変数の値が他の独立変数の値に影響を及ぼすことはありません。しかし、このような理想的な状況が現実の世界で起こることはまれです。独立変数が相関関係にある場合、すなわち、冗長な情報が含まれている場合、その回帰モデルのパラメータ推定値は、信頼できないものになる可能性があります。回帰モデルのパラメータは、各独立変数の固有の寄与を理論的に数値化して従属変数を予測します。もし独立変数どうしに相関関係があれば、それらの間には共通する何らかの情報が含まれているので、パラメータの推定値が「汚染」されることになります。この多重共線性 (multicollinearity) が高ければそのパラメーターの推定値は信頼できないものになります。詳しくは、影響点の対処法をご覧ください。多重共線性 (multicollinearity) には以下の２つのタイプがあります：
- Structural Multicollinearity (構造的多重共線性)：構造的多重共線性が生じるのは、回帰方程式に互いに影響を及ぼしあう複数の独立変数が含まれている場合です。構造的多重共線性が生じる最も一般的な形式は、多項式回帰方程式の独立変数が幾つかの累乗 (power) になっている場合です。このような累乗 (例えば、x, x², … など) には互いに相関関係があるので構造的多重共線性が生じます。回帰方程式に交互作用項を含める場合も、構造的多重共線性が生じることがあります。
- Sample-Based Multicollinearity (標本に基づく多重共線性)：標本に基づく多重共線性が生じるのは、独立変数が相関するような方法で標本となる観測データが収集されている場合です (例えば、年齢の異なる児童に関して年齢、身長、および、体重を収集したとすれば、各変数の間には互いに相関関係があります)。
SigmaPlot では、VIF (Variance inflation factor) を使って多重共線性のある独立変数を自動的に検出することができます。
多重共線性のデータにフラッグを付ける：Flag Values > 編集ボックスの値を多重共線性変数の閾値として使います。デフォルトの閾値は 4.0 で、これは、4.0 より大きい値はいずれも多重共線性としてフラッグが付くことを意味します。この多重共線性の検出をより敏感にするには、この値を小さくします。そのデータに多重共線性があるというフラッグが付く前に、独立変数の相関関係を許容する範囲を広げるには、この値を大きくします。VIF ( variance inflation factor) が大きければ、その回帰モデルに余分な変数が存在することになり、パラメータ推定値が信頼できないものになります。VIF ( variance inflation factor) の値が 4 より大きければ、多重共線性の可能性が提示されます。この値が 10 より大きければ、多重共線性が深刻であることをあらわします。
Report Flagged Values Only (フラッグを立てた値のみレポートする) ：影響力ポイント検定でフラッグが立てられた影響力のポイントだけをレポートに含める場合は、Report Flagged Values Only を選択します。このオプションを解除すると影響力のある全てのポイントがレポートに含まれることになります。

4.4.1 影響点の対処法

影響点には次の２つの原因があります：

観測データやデータ入力のエラーによってそのデータポイントに何らかの瑕疵が生じている場合。
モデル自体に誤りがある場合。

データの収集や入力に誤りがあった場合は、その値を修正してください。修正する値がわからなければ、そのデータポイントの削除を判断できるかもしれません。モデルに誤りがあるようであれば、回帰の独立変数を変更するか、非線形回帰をお試しください。

4.4.2 多重共線性の対処法

標本に基づく多重共線性 (Sample-based multicollinearity) は、他の条件下でデータを多く収集して独立変数間の相関関係を無くすことで解消される場合があります。もし解消できなければ、その回帰方程式のパラメーターは過剰であることになり、単一または複数の独立変数を取り除くことで多重共線性を排除する必要があります。

構造的多重共線性 (structural multicollinearities) は、累乗や交互作用項ができる前に独立変数を中心化することによって解消することができます。

5. 多重線形回帰を実行する

多重線形回帰 (Multiple Linear Regression) を実行するには、検定するデータを選択する必要があります。検定ウィザードの Select Data パネルを使用して、検定したいデータを含むワークシートの列を選択します。

多重線形回帰を実行するには：

検定を実行する前にデータを選択したい場合は、データ範囲をマウスポインタでドラッグしておきます。
Analysis タブをクリックします。
SigmaStat グループの Tests ドロップダウンリストから以下を選択します：Regression → Multiple Linear検定ウィザードの Select Data パネルが表示されます。検定を選択する前に列を選択していれば、Selected Columns リストにその列が表示されます。列を選択していなければ、データ選択の指示がダイアログボックスに表示されます。
Selected Columns リストに別のワークシート列を割り当てたい場合には、ワークシートで直接その列を選択するか、Data for Dependent または Data for Independent ドロップダウンリストからその列を選択します。Selected Columns リストの Dependent 行に割り当てられるのは最初に選択した列で、リストの Independent 行に２列目以降が割り当てられます。各行には、選択した列の番号またはタイトルが表示されます。 Independent 行には最大 64 列を選択できます。
選択した内容を変更するには、リストの割り当てを選択したあと、ワークシートから列を選択しなおします。Selected Columns リストの内容をダブルクリックすることによって、列の割り当てを消去することもできます。
Finish をクリックすると、回帰が実行されます。正規性と等分散性、残差の独立性を検定するよう指定している場合、SigmaPlot は、正規性 (Shapiro-Wilk または Kolmogorov-Smirnov)、等分散性、残差の独立性を検定します。もしデータに関するこれらの検定のいずれかが棄却されると、SigmaPlot によりその旨が報告されます。検定が完了すると、Multiple Linear Regression の結果をあらわすレポートが表示されます。残差 (Residual) とその他の結果をワークシートに配置するよう選択している場合は、指定した列にそれらが配置され、それぞれラベルが付けられます。

6. 多重線形回帰の結果を解釈する

多重線形回帰のレポートには、方程式と算出された係数、R, R²、および、調整済み R²、従属変数の推定量に関する各種統計値のテーブル、および、回帰方程式と個々の係数の P 値が表示されます。

レポートに表示されるその他の結果は、Options for Linear Regression ダイアログボックスで有効または無効にすることができます。

結果の説明

数値による結果に加えて、拡張された結果の説明が表示されることがあります。この説明テキストは、Options ダイアログボックスで有効または無効にすることができます。表示される小数点以下の桁数についても Options ダイアログボックスで指定できます。

6.1 回帰方程式

係数の値が配置された方程式です。この方程式は以下の形式になります：

y=b₀+b₁x₁+b₂x₂+b₃x₃+…b_kx_k

ここで、 y は従属変数、x₁, x₂, x₃, …, x_k は独立変数、b₁, b₂, b₃ …b_k は回帰係数です。

観測数 N、および、回帰から除外された欠損値を含む観測数 (もしある場合) も表示されます。

6.2 重相関係数 R、決定係数 R Squared、自由度調整済み決定係数 Adj R Squared

R と R²：重相関係数 (multiple correlation coefficient) R と決定係数 (coefficient of determination) R² は、いずれも回帰モデルがどれだけうまくデータを説明しているかを評価する指標です。R 値が 1 に近いほど、その方程式が独立変数と従属変数の間の関係をうまく説明していることをあらわします。独立変数の値から従属変数の値を全く予測できないときは、R が 0 となります。また、独立変数から従属変数を完全に予測できるときは 1 となります。
自由度調整済み決定係数：自由度調整済み決定係数 (adjusted R2, R²_adj) も、回帰モデルがどれだけうまくデータを説明しているかを評価する指標ですが、独立変数の数に自由度を反映させます。R²_adj の値が大きいほど (1 に近いほど) その方程式が独立変数と従属変数の間の関係をうまく説明していることをあらわします。

6.3 推定量の標準誤差

推定量の標準誤差 (standard error of the estimate) s_y|x は、推定する母集団の回帰平面に対する実際のばらつきを評価する指標です。推定する母集団は、観測される標本の２標準誤差の範囲におさまるのが一般的です。

6.4 統計量のサマリーテーブル

Coefficients：回帰モデルの定数 (切片) と独立変数の係数 (傾き) の値が一覧で表示されます。
Standard Error：回帰係数の標準誤差 (Std. Error) です (平均の標準誤差と類似)。推定する母集団の真の回帰係数は、観測された標本の係数の２標準誤差の間に収まるのが一般的です。標準誤差が大きければ、多重共線性の可能性があることを示します。

これらの値は、回帰の t 値と信頼区間の計算に使用されます。

6.5 Beta (標準化係数 β_i)

回帰方程式の係数を無次元の値に標準化したものです。

ここで、b₁ = 回帰係数、s_{x_i} = 独立変数 x_iの標準偏差、そして、 s_y = 従属変数 y の標準偏差です。

この結果は、Regression Options ダイアログボックスで Standardized Coefficients オプションを無効にしない限り表示されます。

t 統計量：t 統計量は、独立変数の係数がゼロである、すなわち、独立変数が従属変数の予測に寄与しないとする帰無仮説を検定します。t は、回帰係数 (regression coefficient) をその標準誤差 (standard error) で割った比です。

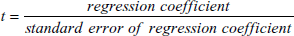
t 値が大きければ、その独立変数を従属変数の予測に使用できる (例えば、係数はゼロではない) と結論づけることができます。
P 値： P は、t に関する P 値を計算したものです。P 値は、回帰係数がゼロではないと誤って結論付ける確率です (すなわち、t に基づいて帰無仮説を誤って棄却する、すなわち、第1種の過誤 (Type I error) を犯す確率です)。P 値が小さいほど、係数がゼロでない確率は高くなります。伝統的に P < 0.05 であれば、独立変数を従属変数の予測に使うことができると結論付けることができます。
VIF (Variance Inflation Factor)：VIF (Variance Inflation Factor) は、多重共線性の尺度です。ある独立変数に関する回帰パラメーター (係数) の標準誤差が、それ以外の独立変数に含まれる余計な情報によってどれだけ「ふくらむ (inflation)」かを測定します。VIF が 1.0 の場合、他の独立変数には余計な情報が無いことになります。VIF が非常に大きければ、その回帰モデルに余計な変数が存在することになり、そのパラメーターの推定値は信頼できないものになります。独立変数の VIF の値が指定した値より大きければ、他の独立変数に多重共線性があることを示す > 記号のフラッグが付きます。提示される値は 4.0 です。

6.6 分散分析表

ANOVA テーブル (分散分析表) には、回帰の ANOVA 統計量と、それに対応する F 値が表示されます。

SS (Sum of Squares：平方和) ：平方和 (SS: Sum of Squares) は、従属変数のばらつきの測度です。
- 回帰 (Regression) の平方和は、従属変数の平均値からの回帰平面の差の測度です。
- 残差 (Residual) の平方和は、残差サイズの測度、すなわち、従属変数の測定値と回帰モデルで予測された値の差です。
- 全体 (total) の平方和は、従属変数全体の平均値に関する変動の測度です。
DF (Degrees of Freedom：自由度)：自由度 (DF: Degrees of freedom) は、測定データや回帰方程式の変数の数をあらわします。
- 回帰 (regression) の自由度は、独立変数の数の測度です。
- 残差 (residual) の自由度は、観測データの数から方程式の項の数を差し引いた測度です。
- 全体 (total) の自由度は、全観測データの測度です。
MS (Mean Square：平均平方)：平均平方 (MS: Mean Square) は、母分散に関する２つの推定値を求めます。これら２つの分散推定値の比較が分散分析の基礎となります。回帰 (Regression) の平均平方は、従属変数の平均値からの回帰のばらつきの測度です。次式で与えられます：

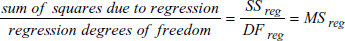
残差平均平方 (residual mean square) は、回帰直線に関する残差のばらつきの測度です。次式で与えられます：

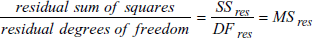
残差平均平方は、S ²_y|xとも等しくなります。
F 統計量：F 検定の統計量は、従属変数の予測における独立変数の寄与 (contribution) の尺度です。次の比率で表されます：

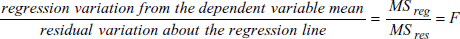
F が大きな値である場合は、独立変数が従属変数の予測に寄与していると結論付けることができます (すなわち、係数の少なくとも１つがゼロでなく、かつ、説明できないばらつき (unexplained variability) が、無作為抽出した従属変数の平均に関するばらつきの期待値より小さい場合) 。F 比が 1 に近いときは、変数間には関連性がないと結論付けることができます (すなわち、このデータは、すべての標本がランダムに分布しているという帰無仮説と合致します)。
P Value：P 値は、従属変数と独立変数の間に誤って関連性があると結論付ける確率です (すなわち、F に基づいて帰無仮説を誤って棄却する、すなわち、第1種の過誤 (Type I error) を犯す確率です)。P 値が小さいほど、関連性のある確率が高くなります。伝統的に P < 0.05 であれば、独立変数を従属変数の予測に使うことができると結論付けることができます。

6.7 増分平方和

SSincr：増分 (incremental) 平方和、すなわち、タイプ I 平方和 SSincr は、ある独立変数を方程式に加えるたびに更新される予測情報の尺度です。増分平方和は、ある独立変数を回帰方程式に追加したときに得られる回帰平方和を、全ての独立変数について逐次的に求め、その増加分 (および残差平方和の減少分) をそれぞれ測定します。これらの値を比較することで、独立変数を追加したときの寄与をそれぞれ調べることができます。
SSmarg：周辺 (marginal) 平方和、すなわち、タイプ III 平方和 SSmarg は、ある独立変数に含まれる唯一の予測情報について、その独立変数を除く全ての独立変数を計算して得られる尺度です。これらの値を比較することで、各独立変数の単独の寄与を調べることができます。周辺平方和では、方程式内のある独立変数を除く全ての変数を投入したあと、その独立変数を最後に投入することによって得られる残差平方和の減少分を測定します。

6.8 PRESS 統計量

PRESS (Predicted Residual Error Sum of Squares：予測残差平方和) は、ある回帰モデルが観測データをどれだけうまく予測できるかを評価する尺度です。PRESS 統計量は、予測誤差 (予測値と実測値の差) の二乗を観測データ毎に合計するもので、推定する回帰モデルの計算からは当該データは除外して算出します。PRESS 統計量のひとつの重要な用途は、モデルの比較です。同一データに幾つかの回帰モデルを当てはめた場合、PRESS 統計量の最も小さいモデルが最も予測能力が高いものとなります。

6.9 Durbin-Watson 統計量

Durbin-Watson 統計量は、残差間の相関の測度です。残差間に相関がない場合、Durbin-Watson 統計量は 2 になります。この値が 2 から離れるほど、残差間の相関の尤度 (likelihood) は高くなります。この結果は、Regression Options ダイアログボックスでこれを選択していれば表示されます。回帰モデルでは、その残差が互いに独立していると仮定します。Durbin-Watson 検定はこの前提条件のチェックに使用します。Durbin-Watson 値が 2 から Options for Linear Regressionで指定した値だけ外れる場合、レポートに警告が表示されます。提示されるトリガー値の差は、0.50 以上です (例えば、Durbin-Watson 統計量が 1.5 を下回るか 2.5 を上回る場合です)。

6.10 正規性検定

正規性検定 (Normality Test) の結果には、元になる母集団が回帰直線の周囲に正規分布しているという仮説の検定にそのデータが合格 (Passed) したか否か (failed)、および、この検定で算出される P 値が表示されます。いずれの回帰でも、元になる母集団が回帰直線の周囲に正規分布すると仮定します。正規性検定が棄却された場合は、レポートに警告が表示されます。この結果は、検定オプションのダイアログボックスで正規性検定を無効にしない限り表示されます。

正規性検定が棄却された場合は、影響力のある外れ値が存在するか、回帰モデルに誤りがある可能性があります。

6.11 等分散検定

等分散検定 (Constant Variance Test) の結果には、元になる母集団の従属変数のばらつきが独立変数の値にかかわらず一定であるという仮説の検定にそのデータが合格 (Passed) したか否か (failed)、およびこの検定で算出される P 値が表示されます。等分散検定が棄却された場合は、レポートに警告が表示されます。

等分散検定が棄却された場合、別のモデル (例えば、データの形状により近いモデル) の使用を検討するか、または、独立変数を変換してばらつきを安定化することでより精度の高い回帰方程式のパラメータ推定値を得ることを検討してください。

6.12 検出力

この結果は、オプションダイアログボックスでこのオプションを選択している場合に表示されます。回帰モデルの検出力 (Power)、すなわち感度は、推定する母集団に関連性がある場合、それらの関係をモデルが正しくあらわす確率です。

回帰モデルの検出力は、測定データの数、誤って差があるとレポートする危険率 (アルファ)、および回帰の傾きに影響を受けます。

Alpha (アルファ)：アルファ (α) は、そのモデルが本当は誤っているのに正しいと結論付けてしまうことを許容する確率です。アルファ (α) の誤りを、第1種の過誤 (Type I error) と呼ぶこともあります (第1種の過誤は、関係がないという仮説が真であるのに、棄却してしまう場合です)。この値は、オプションダイアログボックスの Power で設定します。提示される値は α = 0.05 で、20分の１の確率で誤りを許容するという設定になります。アルファ (α) の値を小さくするほど、そのモデルが正しいと結論付ける要件はより厳密になりますが、反対に、そのモデルが実際は正しいにもかかわらず誤りであると結論づけてしまう可能性は高くなります (第2種の過誤)。アルファの値を大きくしてモデルを正しいと結論付ける条件を緩和すると、誤ったモデルを採用してしまう危険率も高くなります (第1種の過誤)。

6.13 回帰診断

回帰診断の結果には Options for Multiple Linear Regression ダイアログボックスで選択した予測値、残差、および、その他の診断結果のみが表示されます。外れ値として評価された全ての結果には、< 記号でフラッグが付けられます。外れ値としてフラッグを付ける残差の値は、Options for Multiple Linear Regression ダイアログボックスで設定します。

Report Cases with Outliers Only (※) を選択していれば、単一または複数の残差に外れ値としてフラッグの付いた観測データだけがレポートされます。その観測データのその他の結果は全て表示されます。(※ v14 では Report flagged values only)

Row (行)：これは、測定データの行番号です。
Predicted Values (予測値) ：これは、各測定データについて、回帰モデルによって予測された従属変数の値です。
Residuals (残差)：生の残差で、従属変数に関する測定値と予測値の差です。
Standardized Residuals (標準化残差)：標準化残差 (Standardized Residuals) は、生の残差を推定量の標準誤差 S _y|x で割ったものです。この残差が回帰モデルの周囲に正規分布していれば、標準化残差の約 66% は、-1 から +1 の間の値をとり、標準化残差の約 95% は、-2 から +2 の間の値をとります。標準化残差の値が大きいほど、その点は回帰モデルから離れていることを示します。値が -2.5 より小さい場合、もしくは、2.5 より大きい場合は、そのケースが外れ値である可能性があります。
Studentized Residuals (スチューデント化残差)：スチューデント化残差 (Studentized residual) は、従属変数の予測値の信頼性についてデータセットの中央を高く考慮する標準化残差です。極端なデータポイント (独立変数の最小値と最大値を持つデータポイント) の残差の値に重みを付けることによって、標準化残差に比べて外れ値の検出の感度が高くなります。回帰に関する指定した信頼区間の外側にあるスチューデント化 (Studentized) およびスチューデント化削除 (Studentized deleted) 残差はいずれも、外れ値としてフラッグが付けられます。提示される信頼区間は 95% です。この残差は、全データを使って推定量の標準誤差を計算することから、内部スチューデント化残差 (internally Studentized residual) とも言われています。
Studentized Deleted Residuals (スチューデント化削除残差)：外部スチューデント化残差 (externally Studentized residual) とも言われる、スチューデント化削除残差 (Studentized deleted residual) は、推定量の標準誤差 S_y|x(-i)を使用し、この残差に関係するデータポイントを削除した後に計算を行うスチューデント化残差です。分散の計算からこのデータポイントを削除することによって、外れ値に対する影響が大きくなります。回帰に関する指定した信頼区間の外側にあるスチューデント化 (Studentized) およびスチューデント化削除 (Studentized deleted) 残差はいずれも、外れ値としてフラッグが付けられます。提示される信頼区間は 95% です。スチューデント化削除残差は、スチューデント化残差よりも外れ値に対して遥かに大きな値を算出するので、スチューデント化残差に比べて外れ値の検出の感度が高くなります。

6.14 影響診断

影響診断の結果にはオプションダイアログボックスの Other Diagnostics タブで選択した結果の値だけが表示されます。外れ値として評価された全ての結果には、< 記号でフラッグが付けられます。外れ値としてフラッグを付ける残差の値は、Options for Linear Regression ダイアログボックスの Other Diagnostics タブで設定します。

Report Cases with Outliers Only (※) を選択していれば、単一または複数の残差に外れ値としてフラッグの付いた観測データだけがレポートされます。その観測データのその他の結果も表示されます。(※ v14 では Report flagged values only)

Row (行)：これは、測定データの行番号です。Cook’s Distance (クックの距離)：クックの距離 (Cook’s Distance) は、回帰方程式のパラメータ推定において各点が有する影響力の大きさを評価する尺度です。これは、評価する点を分析から除外したとき回帰係数の値がどれだけ変化するかをはかるものです。値が 1 より大きい場合は、その点に影響力がある可能性を示します。クックの距離が 4 より大きい場合、その点は、パラメータ推定値に対して大きな影響があることを示します。ある点のクックの距離が指定した値より大きい場合、影響力があるとしてフラッグが付けられます。提示される値は 4 です。
Leverage (てこ比)：レバレッジ (Leverage：てこ比) の値は、影響力をもつ可能性のある点を識別します。観測データのレバレッジが期待されるレバレッジより大きい場合は、その点に影響力がある可能性があります。提示されるてこ比の値は、期待値の 2.0 倍です。データポイントのてこ比の期待値は次式であらわされます：

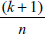
ここで、k は独立変数の数、n はデータポイントの数です。

レバレッジの計算には従属変数しか使用しませんので、独立変数の極値 (大きい値と小さい値) がレバレッジの高い点になる傾向があり、このような点では、独立変数のわずかな変化が従属変数の予測値に大きな影響を与える可能性があります。
DFFITS：DFFITS 統計量は、回帰予測におけるデータポイントの影響力の測度です。あるデータポイントに関して、回帰係数を計算する前にその測定値をデータセットから除外したときの標準誤差の違いを推定した数です。データポイントを除外したときに指定した標準誤差より大きく変化する予測値には、影響力があるというフラッグがつけられます。提示される標準誤差の値は、2.0 です。

6.15 信頼区間

これらの結果は、Options for Multiple Linear Regression ダイアログボックスで選択している場合に表示されます。信頼区間にゼロが含まれていなければ、指定した信頼水準でその係数はゼロではないと結論付けることができます。これは、 P < α (alpha) としても表現できます。ここで、α は、係数はゼロではないと誤って結論付けてもよしとする確率で、信頼区間は 100(1 – α) となります。

信頼水準は、1 から 99 までの任意の値を指定できます。提示される信頼水準はいずれの区間についても 95% です。

Row (行) ：これは、測定データの行番号です。
Predicted (予測値) ：この列は回帰モデルによって予測される測定データ毎の従属変数の値です。
Regression：回帰直線の信頼区間では、指定した信頼水準について従属変数と独立変数との間の真の関係を含む領域を計算した変数の値の範囲が表示されます。
Population：母集団の信頼区間では、指定した信頼水準について観測データを抽出した母集団を含む領域を計算した変数の値の範囲が表示されます。

7. 多重線形回帰のレポートグラフ

多重線形回帰の結果を使用して、以下に示す最大６つのグラフを作成することができます：

残差のヒストグラム (Histogram of Residuals)：詳しくは、残差のヒストグラム (Histogram of Residuals) をご覧ください。
残差の散布図 (Scatter plot of the residuals)：詳しくは、残差の散布図 (Scatter Plot of the Residuals) をご覧ください。
標準化残差の棒グラフ (Bar Chart of the Standardized Residuals)：詳しくは、標準化残差の棒グラフ (Bar Chart of the Standardized Residuals) をご覧ください。
残差の正規確率プロット (Normal probability plot of the residuals)：詳しくは、正規確率プロット (Normal Probability Plot) をご覧ください。
１独立変数の回帰変数と信頼および予測区間の折れ線/散布図 (Line/scatter plot of the regression variable and confidence and prediction intervals with one independent)：詳しくは、予測および信頼区間付き 2D 回帰直線と散布図 (2D Line/Scatter Plots of the Regressions with Prediction and Confidence Intervals) をご覧ください。
残差の 3D 散布図 (3D scatter plot of the residuals)：詳しくは、残差の 3D 散布図 (3D Residual Scatter Plot) をご覧ください。

7.1 多重線形回帰のレポートグラフを作成する

多重線形回帰データのレポートグラフを作成するには：

Multiple Linear Regression レポートを表示した状態で、Report タブをクリックします。
Result Graphs グループにある Create Result Graph をクリックします。
Create Result Graph ダイアログボックスに Multiple Linear Regression の結果で使用できるグラフのタイプが表示されます。
Graph Type リストから作成したいグラフのタイプを選択して、OK をクリックするか、リストから作成したいグラフをダブルクリックします。Scatter Plot Residuals, Bar Chart Std Residuals, Regression, Conf.
& Pred を選択した場合、そのグラフに使用したい独立変数の列を選択するよう指示するダイアログボックスが表示されます。3D Scatter & Mesh, または 3D Residual Scatter を選択し、かつ、独立変数の列を複数選択している場合は、そのグラフに使用したい独立変数の２列を選択するよう指示するダイアログボックスが表示されます。
グラフで使用したい独立変数を含む列を選択したら、OK をクリックします。指定した独立変数を使用したグラフが表示されます。詳しくは、レポートグラフをご覧ください。