23.7 ベストサブセット回帰

線形ベストサブセット回帰 (Linear Best Subsets Regression) を使うのは：

データを通る直線または平面 (超平面) を当てはめることによって、データの傾向を予測する必要があるとき、すなわち、ある変数の値をそれ以外の単一または複数の変数の値から予測したいとき。
従属変数の予測にどの独立変数が寄与するか分からないので、従属変数の予測に最も寄与する独立変数のサブセットを求めたいとき。

独立変数は、予測変数とも呼ばれる既知の変数です。独立変数を変化させると、それに対応する従属変数 (応答変数ともいう) の値が決まります。

使用する独立変数がどれであるかが既に分かっている場合は、多重線形回帰 (Multiple Linear Regression) を使います。モデルに変数を逐次的に追加したり除外していくことによって、方程式モデルを選択したい場合は、段階的回帰 (Stepwise Regression) を使います。直線や平面ではない関係の場合は、多項式回帰 (Polynomial) または非線形回帰 (Nonlinear Regression) を使います。

ベストサブセット回帰について
「ベスト」サブセットの判定基準
ベストサブセット回帰を実行する
ベストサブセット回帰のデータを配置する
ベストサブセット回帰オプションを設定する
1. Options for Best Subset Regression: Criterion
  1. 多重共線性データにフラッグを付ける
ベストサブセット回帰を実行する
ベストサブセット回帰の結果を解釈する
1. サマリーテーブル
2. 各サブセットの結果

1. ベストサブセット回帰について

ベストサブセット回帰 (Best Subsets Regression) は、独立変数の異なる組み合わせを系統的に調べ、従属変数の予測に最も寄与する変数のサブセット (最有力候補) を選択することで多重線形回帰の変数を選び出す手法です。

ベストサブセット回帰では、独立変数と従属変数との関係が以下の多次元平面の一般方程式で当てはめられることが仮定されます：

y = b₀+b₁x₁+b₂x₂+b₃x₃+…b_kx_k

ここで、y は従属変数、x₁, x₂, x₃…, x_k は独立変数、そして、b₁, b₂, b₃…, x_k は回帰係数です。x_i の値を変化させると、それに対応する y の値も増加または減少します。ベストサブセット回帰では、従属変数の予測が「ベスト」になるような独立変数の組み合わせを求めます。「ベスト」であるという判定基準 (criteria) には幾つかの種類がありますので、選択する基準に応じてその結果は変わります。これらの判定基準は、Options for Best Subset Regression ダイアログボックスで指定します。

ベストサブセット回帰では、予測値、残差、グラフ、その他の結果は出力されません。これらの結果を表示させたい場合は、そのモデルで使用した独立変数を書き留めた後、その独立変数だけを使って多重線形回帰を実行してください。

2. 「ベスト」サブセットの判定基準

従属変数の予測に寄与する「ベスト」な変数のサブセットはどれであるかを評価する統計量は３つあります。

R Squared：重回帰の決定係数 R² は、その回帰モデルがどれだけ良くデータを説明するかをはかる尺度です。R² の値が大きいほど、従属変数をうまく予測するモデルになります。ただし、方程式で使用する変数の数は考慮されません。従って、変数の追加が予測に真に寄与するか否かにかかわらず、変数の多い方程式ほど、R² の値は高くなります。
Adjusted R Squared：R²_adj (調整済み R²) は、その回帰モデルがどれだけ良くデータを説明するかを R² に基づいてはかる尺度ですが、独立変数の数が考慮される点が異なります。
Mallows：C_p は、従属変数の推定において、その回帰方程式から独立変数を除外することでもたらされる偏りの大きさをはかる尺度で、パラメーターの数に従属変数の予測平均と真の母平均との差の尺度を加えて計算します。C_p の最適値は、パラメーター (サブセットで使用する独立変数と定数) の数と等しく、次式で与えられます：
C_p = p = k +1

ここで、p はパラメーター数、k は独立変数の数です。

C_p の値がパラメーター数に近づくほど、妥当性のある変数が除外されることは希になります。なお、条件を完全に満たすモデルは常に C_p=p となります。

3. ベストサブセット回帰を実行する

ベストサブセット回帰を実行するには：

ワークシートに適切なデータを入力または配置します。詳しくは、ベストサブセット回帰のデータを配置するをご覧ください。
必要があれば、Best Subset Regression オプションを設定します。
Analysis タブをクリックします。
SigmaStat グループにある Tests ドロップダウンリストから以下を選択します：Regression → Best Subsets
Best Subset Regression レポートを表示して内容を解釈します。詳しくは、ベストサブセット回帰の結果を解釈するをご覧ください。

4. ベストサブセット回帰のデータを配置する

観測した従属変数のデータを１列に配置し、それに対応する独立変数のデータを単一または複数の列に配置します。欠損値を含む観測データは無視されます。また、全ての列は長さを等しくする必要があります。

5. ベストサブセット回帰オプションを設定する

ベストサブセット回帰オプションを使用するのは：

従属変数の予測に使う判定基準と、方程式で使用するサブセットの数を指定するとき。
VIF (variance inflation factor) を有効にして、回帰パラメータの推定を困難にする要因 (多重共線性) を判断するとき。

ベストサブセット回帰オプションを変更するには：

検定オプションの変更後に検定を実行するに際して、検定の実行前にデータを選択しておきたい場合は、対象とするデータ列をポインターでドラッグしておきます。
Analysis タブの SigmaStat グループにある Select Test ドロップダウンリストから Best Subset Regression を選択します。
Options をクリックします。Options for Best Subset Regressionダイアログボックスに Criterion タブが表示されます。詳しくは、Options for Best Subset Regression: Criterion をご覧ください。オプションの設定内容は、SigmaPlot を次回起動したときも保持されます。
検定を続行するには、Run Test をクリックします。
現在の設定内容を適用して、オプションダイアログを閉じるには、OK をクリックします。

5.1 Options for Best Subset Regression: Criterion

ベストサブセットの決定に使用する判定基準を選択するには、Best Criterion オプションを、リストするサブセットの数を指定するには Number of Subsets オプションを使います。

Best Criterion：ベストサブセットを決定する判定基準をドロップダウンリストから選択します。
- Mallows：Best Criterion ドロップダウンリストから Mallows Cp を選択すると、変数を除外したときに導入される偏りの尺度を使用して、多数の変数候補を素早く評価し、妥当性のある変数のみを含む少数のサブセットを出力します。リストされるサブセットの数は、Number of Subsets オプションで指定した数と同じになります。
- R Squared：Best Criterion ドロップダウンリストから R Squared (R²) を選択すると、決定係数の最大値を使用して、当てはまりの最も良いサブセットが求められます。R² には、使用した変数の数に関する情報は含まれませんので、サブセットは候補変数の数ごとにリストされます (例えば、独立変数が１の場合、変数が２つの場合、という具合に、全ての変数が選択されるまで)。候補変数の数ごとにリストされるサブセットの最大数は、Number of Subsets オプションで指定した数と同じになります。
- Adjusted R Squared：Best Criterion ドロップダウンリストから Adjusted R Squared (Adjusted R²) を選択すると、R²_adj の最大値を使って最適な回帰を選び出します。R²_adj では、回帰方程式に独立変数を追加したときの自由度の損失が考慮されます。リストされるサブセットの数は、Number of Subsets オプションで指定した数と同じになります。
Number of Subsets：一覧で表示される最も寄与する変数グループの数を指定するには、このオプションを使って、Number of Subsets 編集ボックスに目的とする値を入力します。C_p の場合は、この値はサブセットの総数になります。R² の場合は、方程式内の独立変数の数毎にリストされる変数サブセットの数になります。
Variance Inflation Factor：Variance Inflation Factor オプションを使うと、独立変数の多重共線性、すなわち、当てはめにおける独立変数の線形結合が測定されます。回帰プロシージャーでは、独立変数は統計的に互いに独立であることが仮定されます。例えば、ある独立変数の値が他の独立変数の値に影響を及ぼすことはありません。しかし、このような理想的な状況が現実の世界で起こることはまれです。独立変数が相関関係にある場合、すなわち、冗長な情報が含まれている場合、その回帰モデルのパラメータ推定値は、信頼できないものになる可能性があります。回帰モデルのパラメータは、各独立変数の固有の寄与を理論的に数値化して従属変数を予測します。もし独立変数どうしに相関関係があれば、それらの間には共通する何らかの情報が含まれているので、パラメータの推定値が「汚染」されることになります。この多重共線性 (multicollinearity) が高ければそのパラメーターの推定値は信頼できないものになります。多重共線性 (multicollinearity) には以下の２つのタイプがあります：
- Structural Multicollinearity (構造的多重共線性)：構造的多重共線性が生じるのは、回帰方程式に互いに影響を及ぼしあう複数の独立変数が含まれている場合です。構造的多重共線性が生じる最も一般的な形式は、多項式回帰方程式の独立変数が幾つかの累乗 (power) になっている場合です。このような累乗 (例えば、x, x², … など) には互いに相関関係があるので構造的多重共線性が生じます。回帰方程式に交互作用項を含める場合も、構造的多重共線性が生じることがあります。
- Sample-Based Multicollinearity (標本に基づく多重共線性)：標本に基づく多重共線性が生じるのは、独立変数が相関するような方法で標本となる観測データが収集されている場合です (例えば、年齢の異なる児童に関して年齢、身長、および、体重を収集したとすれば、各変数の間には互いに相関関係があります)。
Report Flagged Values Only (フラッグを立てた値のみレポートする) ：影響力ポイント検定でフラッグが立てられた影響力のポイントだけをレポートに含める場合は、Report Flagged Values Only を選択します。このオプションを解除すると影響力のある全てのポイントがレポートに含まれることになります。詳しくは、多重共線性データにフラッグを付けるをご覧ください。

5.1.1 多重共線性データにフラッグを付ける

Flag Values > 編集ボックスの値を多重共線性変数の閾値として使います。デフォルトの閾値は 4.0 で、これは、4.0 より大きい値はいずれも多重共線性としてフラッグが付くことを意味します。この多重共線性の検出をより敏感にするには、この値を小さくします。そのデータに多重共線性があるというフラッグが付く前に、独立変数の相関関係を許容する範囲を広げるには、この値を大きくします。VIF ( variance inflation factor) が大きければ、その回帰モデルに余分な変数が存在することになり、パラメータ推定値が信頼できないものになります。VIF ( variance inflation factor) の値が 4 より大きければ、多重共線性の可能性が提示されます。この値が 10 より大きければ、多重共線性が深刻であることをあらわします。
多重共線性の対処法：標本に基づく多重共線性 (Sample-based multicollinearity) は、他の条件下でデータを多く収集して独立変数間の相関関係を無くすことで解消される場合があります。もし解消できなければ、その回帰方程式のパラメーターは過剰であることになり、単一または複数の独立変数を取り除くことで多重共線性を排除する必要があります。構造的多重共線性 (structural multicollinearities) は、累乗や交互作用項ができる前に独立変数を中心化することによって解消することができます。

6. ベストサブセット回帰を実行する

ベストサブセット回帰 (Best Subset Regression) を実行するには、検定するデータを選択する必要があります。検定ウィザードの Select Data パネルを使用して、検定したいデータを含むワークシートの列を選択します。

ベストサブセット回帰を実行するには:

検定を実行する前にデータを選択したい場合は、データ範囲をマウスポインタでドラッグしておきます。
Analysis タブをクリックします。
SigmaStat グループの Tests ドロップダウンリストから以下を選択します：Regression→Best Subsets検定ウィザードの Select Data パネルが表示されます。検定を選択する前に列を選択していれば、Selected Columns リストにその列が表示されます。列を選択していなければ、データ選択の指示がダイアログボックスに表示されます。
Selected Columns リストに別のワークシート列を割り当てたい場合には、ワークシートで直接その列を選択するか、Data for Dependent または Data for Independent ドロップダウンリストからその列を選択します。Selected Columns リストの Dependent Variable 行に割り当てられるのは最初に選択した列で、リストの Independent Variable 行に２列目以降が割り当てられます。各行には、選択した列の番号またはタイトルが表示されます。Independent Variable 行には最大 64 列を選択できます。
選択した内容を変更するには、リストの割り当てを選択したあと、ワークシートから列を選択しなおします。Selected Columns リストの内容をダブルクリックすることによって、列の割り当てを消去することもできます。
Finish をクリックすると、回帰が実行されます。ベストサブセット回帰が実行されます。検定が完了すると、Best Subset regression レポートが表示されます。

※ Tip：ベストサブセット回帰では、予測値、残差、グラフ、その他の結果は出力されません。これらの結果を表示させたい場合は、そのモデルで使用した独立変数を書き留めた後、その独立変数だけを使って多重線形回帰を実行してください。」

7. ベストサブセット回帰の結果を解釈する

ベストサブセット回帰レポートには、全ての変数サブセットに関する「ベスト」判定基準の統計量のサマリーテーブルが、誤差の平均平方 (MSerr) とそのサブセット固有のメンバー変数と共に一覧で表示されます。

なお、リストに表示されるサブセットの数は、Options for Best Subsets Regression ダイアログで選択したサブセットの数と、ベストサブセットの選択に使用した判定基準によって決定されます。

R² を使用した場合、レポートに含まれる変数の数毎のサブセットの最大数は、Best Subsets Regression Options ダイアログボックスで設定した数になります。
R² または C_p を使用した場合、レポートされるサブセットの結果の数は、Best Subsets Regression Options ダイアログボックスで設定した数になります。

※ Tip：ベストサブセット回帰では、レポートグラフを作成するこはできません。グラフを表示するには、関心のあるサブセットに含まれる変数を使って多重線形回帰を実行し、それらの結果をグラフ化します。詳しくは、多重線形回帰 (Multiple Linear Regression) をご覧ください。

結果の説明

数値による結果に加えて、拡張された結果の説明が表示されることがあります。この説明テキストは、Options ダイアログボックスで有効または無効にすることができます。表示される小数点以下の桁数についても Options ダイアログボックスで指定できます。

7.1 サマリーテーブル

Variables：サブセットに含まれる変数には、テーブル右側の各変数記号の下にアスタリスク (*) が付けられます。
Mallows： C_p は、従属変数の推定において、その回帰方程式から独立変数を除外することでもたらされる偏りの大きさをはかる尺度です。C_p の最適値は、パラメーター (サブセットで使用する独立変数と定数) の数と等しく、次式で与えられます：
C_p = p = k+1

ここで、p はパラメーターの数、k は独立変数の数です。C_p の値がパラメーター数に近づくほど、妥当性のある変数が除外されることは希になります。下位のサブセットでも、C_p の値が k + 1 に近ければ、ベストサブセット変数の有力な候補になります。
R Squared：重回帰の決定係数 R² は、その回帰モデルがどれだけ良くデータを説明するかをはかる尺度です。R² の値が 1 に近いほど、従属変数を説明するのにふさわしいモデルであることになります。ただし、そこで使用される変数の数は考慮されませんので、変数の追加が予測に真に寄与するか否かにかかわらず、変数の多い方程式ほど、R² の値は高くなります。
Adjusted R Squared：R²_adj (調整済み R²) は、その回帰モデルがどれだけ良くデータを説明するかを R² に基づいてはかる尺度ですが、独立変数の数が考慮される点が異なります。この値が大きいほど (1 に近いほど)、その方程式は独立変数と従属変数との関係を良く説明することになります。なお、全ての変数を含むサブセットは常に C_p = p となります。
MSerr (Error Mean Square)：次式で与えられる誤差の平均平方 (残差、群内) は：

推定する母集団にある変動の推定量で、観測データのランダム成分から算出されます。
Residual Sum of Squares：残差平方和は、従属変数の観測値と回帰モデルによって予測された値との差である残差の大きさをはかる尺度です。

7.2 各サブセットの結果

サマリーテーブルで特定された回帰方程式それぞれに関する統計結果をあらわすテーブルが一覧で表示されます。

Coefficient (係数)：Constant (定数) とその回帰モデルの独立変数それぞれの係数の値が一覧で表示されます。
Std Err (標準誤差)：標準誤差は、回帰係数の推定量です (平均の標準誤差に相当します)。推定する母集団の真の回帰係数は、一般に観測された標本係数のおよそ２標準誤差の範囲内に収まります。標準誤差の値が大きければ、多重共線性の疑いがあります。これらの値は、回帰係数の t 値の算出に使用されます。
t 統計量：t 統計量は、独立変数の係数はゼロである、すなわち、その独立変数は従属変数の予測に寄与しないという帰無仮説をそれぞれ検定します。t 値は、回帰係数とその標準誤差の比で次式であらわされます：

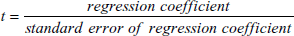
t の値が大きければ、その独立変数は従属変数の予測に使用できるものである (すなわち、その係数はゼロではない) と結論付けることができます。
P 値：P は、t について計算した P 値です。P 値は、従属変数と独立変数の間に誤って真の関係があると結論付ける確率です (すなわち、t に基づいて帰無仮説を誤って棄却する、すなわち、第1種の過誤 (Type I error) を犯す確率です)。P 値が小さいほど、その独立変数が従属変数の予測に寄与する確率が高くなります。伝統的に P < 0.05 であれば、独立変数を従属変数の予測に使うことができると結論付けることができます。
VIF (Variance Inflation Factor)：VIF (Variance Inflation Factor) は、多重共線性をはかる尺度です。ある独立変数に関する回帰パラメーター (係数) が、それ以外の独立変数に含まれる余計な情報によってどれだけ「ふくらむ (inflation)」かを測定します。
VIF が 1.0 かそれに近い場合、その他の独立変数には余計な情報が無いことになります。VIF が非常に大きければ、その回帰モデルに余計な変数が存在することになり、そのパラメーターの推定値は信頼できないものになります。この結果は Options for Best Subset Regression ダイアログボックスでこのオプションを無効にしない限り表示されます。