23.5 多項式回帰

多項式回帰 (Polynomial Regression) を使うのは：

直線上には従わないデータに曲線を当てはめることで、その傾向を予測したいとき、すなわち、ある変数の値を別の変数の値から予測したいとき。
独立変数が唯一であることが分かっているとき。

独立変数は、予測変数とも呼ばれる既知の変数です。独立変数を変化させると、それに対応する従属変数 (応答変数ともいう) の値が決まります。

独立変数と従属変数の関係が１次 (直線) であることが既知である場合は、多重線形回帰 (Multiple Linear Regression) を使います。この関係が線形多項式 (linear polynomial) でない場合は (例えば、対数や指数関数) 、非線形回帰 (Nonlinear Regression) を使います。

多項式回帰について
多項式回帰を実行する
多項式回帰のデータを配置する
多項式回帰オプションを設定する
多項式回帰を実行する
インクリメント型多項式回帰の結果を解釈する
次数のみの多項式回帰の結果を解釈する
多項式回帰のレポートグラフ
1. 多項式回帰のレポートグラフを作成する

1. 多項式回帰について

多項式回帰 (Polynomial Regression) では、独立変数と従属変数の間の関係が、次数 k の多項式であらわされる以下の一般方程式に当てはめられることが仮定されます：

y = b₀+b₁x¹+b₂x²+b₃x³+ … b_kx^k

ここで、y は従属変数、x は独立変数、そして、b₁, b₂, b₃ は回帰係数です。x の値が変化すると、それに対応する値も多項式関数に従って変化します。

多項式の次数 k は、独立変数の指数のうち最大のものです。すなわち、多項式が一次なら直線、多項式の次数が２ (二次) なら放物線といった具合です。

多項式回帰は、パラメトリック検定です。すなわち、ある独立変数が与えられると、その従属変数の取り得る値は分散の等しい正規分布に従うものと仮定されます。

※ Tip：データに多項式を当てはめる場合、独立変数に x、x² 等を使って多重線形回帰を単純に行った場合より、多項式回帰プロシージャーの方が信頼できる結果になります。

2. 多項式回帰を実行する

多項式回帰 (Polynomial Regression) を実行するには：

ワークシートに適切なデータを入力または配置します。詳しくは、多項式回帰のデータを配置するをご覧ください。
多項式回帰オプションを設定します。
Analysis タブをクリックします。
SigmaStat グループにある Tests ドロップダウンリストから以下を選択します：Regression → Polynomial
検定を実行します。
インクリメント型多項式回帰レポートを表示して内容を解釈します。詳しくは、インクリメント型多項式回帰レポートの結果を解釈するをご覧ください。
次数のみの多項式回帰レポートを表示して内容を解釈します。詳しくは、次数のみの多項式回帰の結果を解釈するをご覧ください。
レポートグラフを作成します。詳しくは、多項式回帰のレポートグラフをご覧ください。

3. 多項式回帰のデータを配置する

従属変数のデータを１列に、それに対応する観測した独立変数のデータを別の列に配置します。

欠損値を含む観測データは無視されます。また、全ての列は長さを等しくする必要があります。

4. 多項式回帰オプションを設定する

多項式回帰オプションを使用するのは：

多項式の次数を設定するとき。
実行したい多項式回帰の種類を指定するとき (増分評価または次数のみ)。
前提条件のチェックオプションを設定するとき。
残差を表示したりそれらをワークシートに保存するとき。
信頼区間を表示したりそれらをワークシートに保存するとき。
PRESS 予測誤差や標準化係数を表示するとき。
検出力を表示するとき。

多項式回帰オプションを変更するには：

検定オプションの変更後に検定を実行するに際して、検定の実行前にデータを選択しておきたい場合は、対象とするデータ列をポインターでドラッグしておきます。
Analysis タブを選択します。
SigmaStat グループの Select Test ドロップダウンリストから Polynomial Regression を選択します。
Options をクリックします。Options for Polynomial Regression ダイアログボックスが表示されます。回帰タイプに Incremental Order を選択した場合は、Criterion オプションのみが表示されます。Order Only を選択した場合は、以下のタブが表示されます：
1. Criterion：Criterion タブをクリックすると、Polynomial Order, および
  Regression Type オプションが表示されます。詳しくは、Options for Polynomial
  Regression: Criterion をご覧ください。
2. Assumption Checking：Assumption Checking タブをクリックすると、Normality,
  Constant Variance, および Durbin-Watson オプションが表示されます。詳しくは、Options for Polynomial Regression: Assumption Checking をご覧ください。
3. Residuals：Residuals タブをクリックすると、残差オプションが表示されます。詳しくは、Options for Polynomial Regression: Residuals をご覧ください。
4. More Statistics：More Statistics タブをクリックすると、信頼区間、PRESS 予測誤差、標準化係数オプションが表示されます。
5. Post Hoc：Post Hoc Tests タブをクリックすると、Power オプションが表示されます。詳しくは、Options for Polynomial Regression: Post Hoc Tests をご覧ください。SigmaPlot を次回以降起動するときは、ここで選択したオプションの内容が保持されます。
検定を続行するには、Run Test をクリックします。
現在の設定内容を適用して、オプションダイアログを閉じるには、OK をクリックします。

4.1 Options for Polynomial Regression: Criterion

オプションダイアログの Criterion タブを選択すると、Polynomial Order と Regression オプションが表示されます。これらのオプションを使って、データの評価に使用する多項式の次数と、多項式のタイプを指定します。

Polynomial Order：Polynomial Order ドロップダウンリストから目的とする多項式の次数を選択します。ドロップダウンボックスに値を直接入力することも可能です。ここで指定した値が評価する多項式の最大次数または計算する特定の次数に使用されます。
Order Only：Regression Type ドロップダウンリストから Order Only を選択すると、Polynomial Order 編集ボックスで指定した次数のみがデータに当てはめられます。
Incremental Evaluation：使用する多項式の次数を求める必要がある場合は、Incremental Evaluation を選択します。このオプションを選択すると、多項式の各次数の方程式がゼロからはじまり Polynomial Order ボックスで指定した値まで順番に評価されます。なお、このオプションではいずれの回帰結果も表示されません。その代り最適なモデルに使う次数を評価するのに使用します。次数が定まると、Order only で多項式回帰を実行して、完全な回帰結果を求めます。

4.2 Options for Polynomial Regression: Assumption Checking

オプションダイアログボックスの Assumption Checking タブをクリックすると、Normality, Constant Variance, および Durbin-Watson オプションが表示されます。これらのオプションは、多項式回帰がそのデータについて行う３つの仮説をチェックすることによってお持ちのデータが回帰分析に適合しているかを検定します。多項式回帰で仮定するのは：

元の母集団がその回帰について正規分布していること。
元の母集団の従属変数の分散が独立変数の値 (複数可) とは無関係に一定であること。
残差が互いに独立していること。

デフォルトでは全ての Assumption Checking (前提条件のチェック) オプションが選択されています。これらのオプションは、使用するデータが等分散の正規分布に従っており、その残差が互いに独立であることが確実に分かっているときだけ無効にしてください。

Normality の検定：SigmaPlot では、母集団の分布の正規性検定に Shapiro-Wilk または Kolmogorov-Smirnov のいずれかを使用します。
Constant Variance Testing (等分散性の検定)：SigmaPlot では、等分散性の検定に残差の絶対値と観測された従属変数の値との間のスピアマンの順位相関 (Spearman rank correlation) を計算します。この相関関係が有意であれば等分散性の前提条件は棄却されますので、その場合は、別モデル (例えば、データの形状により密接に従うようなモデル) での試行を検討するか、単一または複数の独立変数の分散安定化の変換を行う必要があります。

P Values for Normality and Constant Variance (正規性と等分散性の P 値)： P 値は、データが正規分布に従っていないと誤って結論付けてしまう確率を決定します (そのデータは正規分布に従っているという帰無仮説を誤って棄却してしまうリスクが P 値です)。ここで設定した P 値よりも、検定で算出された P 値が大きければ検定は採択 (Pass) されます。正規性と等分散のいずれかまたは両方の要件をより厳密なものにするには、この P 値を大きくします。パラメトリックな統計手法では、仮説の棄却が比較的ロバスト (頑健) に検出されることから、SigmaPlot ではこの値を 0.05 としています。P 値をこれよりも大きくすると (例えば、0.10)、そのデータに正規性がないとの判定が出やすくなります。正規性と等分散のいずれか又は両方の要件を緩和するには、P 値を小さくします。正規性があるという仮説を棄却するための P 値に小さい値しか要求しないということは、前提とする正規分布からデータが外れていても、それが非正規であると判定される前に、それだけ広く受け入れたいとする意思があることを意味します。例えば、P 値を 0.01 とした場合、あるデータを非正規であると判定するには、0.05 の場合と比べてそれだけ大きく正規性を逸脱していなければなりません。

※ Note：この前提条件の検定では、非正規や等分散性でない母集団のデータ検出においてロバストな処理がなされますが、データ分布が極端な条件では検出できない場合があります。しかし、このような条件の場合は、前提条件の自動検定に頼らずにデータを視覚的に調べることで容易に検出することができます。

Durbin-Watson 統計量： SigmaPlot では、残差が互いに独立していることを検定するのに Durbin-Watson 統計量を使用します。Durbin-Watson 統計量は、残差間の系列相関を測定するものです。この残差は、多くの場合、独立変数が時間で、かつ、観測値と回帰直線との間のある時点のずれが、前の時点におけるずれと関連性がある場合に相関します。残差間に相関性がない場合、Durbin-Watson 統計量は 2 になります。
Difference from 2 の値：系列相関の根拠とみなす 2.0 からの許容できるずれを Difference from 2.0 ボックスに入力します。算出される 2.0 からのずれである Durbin-Watson 統計量が入力した値より大きければ、残差に独立性がない可能性があることが SigmaPlot によって警告されます。例えば、このずれの値を提示された値 0.50 にすると、Durbin-Watson 統計量の値が 2.5 より大きいか、1.5 より小さい場合に残差に相関性があるというフラッグが立てられます。独立性の条件を厳しくするには、difference from 2.0 の値を小さくします。独立性の条件を緩和するには、difference from 2.0 の値を大きくします。

4.3 Options for Polynomial Regression: Residuals

Options for Polynomial Regression ダイアログボックスの Residuals タブをクリックすると、Predicted Values, Raw, Standardized, Studentized, Studentized Deleted, および Report Flagged Values Only オプションが表示されます。

Predicted Values (予測値)：このオプションを使用すると、独立変数の観測値ごとに従属変数の予測値が計算され、その結果がワークシートに保存されます。予測値をワークシートに含めたくなければ、選択されたチェックボックスをクリックします。予測値をワークシートの列に配置するには、対応するドロップダウンリストから配置先の列番号を選択します。ドロップダウンリストで none を選択し、Predicted Values チェックボックスが選択されている場合は、レポートにはその値が表示されますが、ワークシートには配置されません。
Raw Residuals (生の残差)：生の残差は、従属変数に関する予測値と観測値の差です。生の残差をレポートに含めるには、このチェックボックスが選択されているかを確認してください。生の残差をワークシートに含めたくなければ、選択されたチェックボックスをクリックします。生の残差をワークシートの列に配置するには、対応するドロップダウンリストから配置先の列番号を選択します。ドロップダウンリストで none を選択し、Raw チェックボックスが選択されている場合は、レポートにはその値が表示されますが、ワークシートには配置されません。
Standardized Residuals (標準化残差)：標準化残差は、残差をその推定量の標準誤差で割ったものです。残差の標準誤差は、要するに残差の標準偏差ですので、回帰直線周辺のばらつきの尺度となります。標準化残差をレポートに含めるには、このチェックボックスが選択されていることを確認してください。標準化残差をワークシートに含めるには、このチェックボックスを選択してください。SigmaPlot は、対応するボックスで指定した信頼区間から外れたデータポイントに対して自動的にフラッグを立てます。例えば、データポイントの中心から外れたデータポイントは、標準化残差の値が「大きい」と判断されます。フラッグを立てるデータポイントは、Flag Values > 編集ボックスの値を編集することで変更することができます。提示される残差の値は 2.5 です。
Studentized Residuals (スチューデント化残差)：スチューデント化残差をレポートに含めるには Studentized Residuals を選択します。スチューデント化残差は、データの両極値に対する中央付近の回帰直線の精度の高さを考慮に入れることによって残差を基準化するものです。スチューデント化残差は、スチューデントの t 分布に従う傾向がありますので、t 分布を利用してスチューデント化残差の大きい値を決定することができます。SigmaPlot は、例えば、データポイントの中心から外れたデータポイントに対しては、スチューデント化残差の値が「大きい」というフラッグを自動的に立てます。フラッグで提示されるデータポイントは、回帰母集団の95％信頼区間の外側にあります。
Studentized Deleted Residuals (スチューデント化削除残差)：スチューデント化削除残差は、スチューデント化残差に似ていますが、該当するデータポイントを使わずに、回帰方程式を計算することで値を求める点が異なります。SigmaPlot は、例えば、データポイントの中心から外れたデータポイントに対しては、スチューデント化削除残差の値が「大きい」というフラッグを自動的に立てます。フラッグで提示されるデータポイントは、回帰母集団の95％信頼区間の外側にあります。

※ Note：スチューデント化残差、および、スチューデント化削除残差はいずれも、同じ信頼区間の設定を使って外れ値を判定します。
Report Flagged Values Only (フラッグ値のみレポートする)：レポートにフラッグの立てられた標準化、および、スチューデント化削除残差しか含めない場合は、Report Flagged Values Only を選択してください。

4.4 Options for Polynomial Regression: More Statistics

オプションダイアログの More Statistics タブをクリックすると、信頼区間オプションが表示されます。母集団、回帰、または、両方の信頼区間を設定し、それらをワークシートに保存することができます。

Confidence Interval for the Population：母集団の信頼区間では、観測データを抽出した母集団が含まれる領域を定義する値の範囲を与えます。母集団の信頼区間をレポートに含めるには、Population を選択します。
Confidence Interval for the Regression：回帰直線の信頼区間は、指定した信頼水準で従属変数と独立変数の間に真の平均値の関係が含まれる領域がこの値の範囲によって定義されます。レポートに回帰の信頼区間を含めるには、Regression チェックボックスが選択されているかを確認し、パーセントボックスに信頼水準の値を入力して指定してください。信頼水準は 1 から 99 までの任意の値にすることができます。提示される区間の信頼水準はいずれも 95 % です。レポートに母集団の信頼区間を含めたくない場合は、選択されたチェックボックスをクリックしてください。
信頼区間をワークシートに保存する。信頼区間をワークシートに保存するには、Starting in Column ドロップダウンリストから区間データを保存したい最初の列の列番号を選択します。ワークシートの指定した列以降に選択した区間データが保存されます。
PRESS Prediction Error (PRESS 予測誤差)：PRESS 予測誤差は、回帰方程式がデータにどれだけ良くあてはまっているかを測る尺度です。このチェックボックスを選択した状態にしておけば、PRESS 統計量を用いて方程式の当てはめが評価されます。レポートに PRESS 統計量を含めたくなければ、選択されているこのチェックボックスを解除します。
Standardized Coefficients (標準化係数)：回帰方程式の係数を無次元の値に標準化したものです。

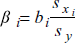
ここで、b_i = 回帰係数、s_xi= 独立変数 x_i の標準偏差、そして、 s_y = 従属変数 y の標準偏差です。

レポートに標準化係数を含めるには、Standardized Coefficients を選択します。標準化係数をワークシートに含めたくない場合は、このオプションを解除します。

4.5 Options for Polynomial Regression: Post Hoc Tests

Options for Polynomial Regression ダイアログボックスの Post Hoc Tests タブをクリックすると Power オプションが表示されます。

回帰の検出力は、観測されたデータの関係性を検出する能力です。アルファ (α) は、誤って関係ありと判断されることを許容する確率です。

多項式回帰データの検出力を計算するには、Power を選択します。アルファ値を変更するには、Alpha Value 編集ボックスの数値を編集します。提示される値は α = 0.05 です。この設定は、誤りを許容する確率が 20分の１であることを示します。すなわち、P < 0.05 であれば有意な関係があると判断できることになります。アルファの値を小さくすると、有意な関係があると結論付ける要件がそれだけ厳格なものになりますが、関係があるにもかかわらず関係がないと結論付ける可能性が高くなります。アルファの値を大きくすると、関係があるとの結論付けが容易になりますが、それだけ誤判定をレポートする危険性が高くなります。

5. 多項式回帰を実行する

多項式回帰 (Polynomial Regression) を実行するには、検定するデータを選択する必要があります。検定ウィザードの Select Data パネルを使用して、検定したいデータを含むワークシートの列を選択します。

多項式回帰を実行するには：

検定を実行する前にデータを選択したい場合は、データ範囲をマウスポインタでドラッグしておきます。
Analysis タブをクリックします。
SigmaStat グループの Tests ドロップダウンリストから以下を選択します：Regression → Polynomial検定ウィザードの Select Data パネルが表示されます。検定を選択する前に列を選択していれば、Selected Columns リストにその列が表示されます。列を選択していなければ、データ選択の指示がダイアログボックスに表示されます。
Selected Columns リストに別のワークシート列を割り当てたい場合には、ワークシートで直接その列を選択するか、Data for Dependent または Data for Independent ドロップダウンリストからその列を選択します。Selected Columns リストのDependent Variable 行に割り当てられるのは最初に選択した列で、２列目が Independent Variable 行に割り当てられます。各行には、選択した列の番号またはタイトルが表示されます。選択を指示される従属変数および独立変数の列はそれぞれ１つずつです。
選択した内容を変更するには、リストの割り当てを選択したあと、ワークシートから列を選択しなおします。Selected Columns リストの内容をダブルクリックすることによって、列の割り当てを消去することもできます。
Finish をクリックすると、回帰が実行されます。正規性と等分散性、残差の独立性を検定するよう指定している場合、SigmaPlot は、正規性 (Shapiro-Wilk または Kolmogorov-Smirnov)、等分散性、残差の独立性を検定します。もしデータに関するこれらの検定のいずれかが棄却されると、SigmaPlot によりその旨が報告されます。検定が完了すると、Polynomial Regression の結果をあらわすレポートが表示されます。ある次数のみを使って回帰を実行しており、予測値、残差、およびその他の検定結果をワークシートに保存するよう設定している場合、指定した列にそれらが配置され、それぞれラベルが付けられます。

※ Remember：ワークシートに結果を得られるのは、次数のみ (Order Only) の多項式回帰を使用した場合のみです。

6. インクリメント型多項式回帰の結果を解釈する

インクリメント型多項式回帰の結果には、各次数ごとの多項式回帰方程式がゼロ次から指定した次数まで順番に表示されます。残差平方和 (MSres) と増分平方和 (MSincr)、および、各次数の方程式の Incremental と Overall の R²、F 値、および、P 値が一覧で表示されます。

結果の説明

数値による結果に加えて、拡張された結果の説明が表示されることがあります。この説明テキストは、Options ダイアログボックスで有効または無効にすることができます。表示される小数点以下の桁数についても Options ダイアログボックスで指定できます。

6.1 回帰方程式

各次数ごとの回帰方程式がそれぞれの係数と共に表示されます。方程式は以下の形式であらわされます：

y = b₀+b₁x¹+b₂x²+b₃x³+ … b_kx^k

ここで、y は従属変数、x は独立変数、そして、b₁, b₂, b₃ は回帰係数です。

多項式の次数 k は、その独立変数の最大の指数です。

インクリメント型の多項式回帰では、次数ゼロから Options for Polynomial Regressions ダイアログボックスで指定した最大次数までの全ての方程式が一覧で表示されます。

6.2 インクリメント型の結果

MSres (残差平均平方)：残差平均平方は、回帰直線に関する残差の変動の尺度です。
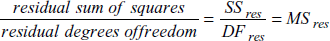
MSincr (増分平均平方)：増分平均平方は、その次数の多項式によって高められた回帰方程式に関する残差変動の減少の尺度です。

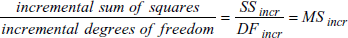
平方和は、従属変数の変動の尺度です。

残差平方和は、従属変数の観測値と回帰モデルによる予測値との間の差である残差の大きさの尺度です。

増分 (incremental) 平方和、すなわち、タイプ I 平方和 SSincr は、ある独立変数を方程式に加えるたびに更新される予測情報の尺度です。

回帰方程式に独立変数の最高次数の項を、それより小さい次数の項をすべて追加した後に追加して得られるその回帰の平方和の増加 (および、残差平方和の減少) の尺度です。各ステップで追加される次数は１なので、DFincr =1 です。
Rsq：R²、すなわち、決定係数は、その回帰モデルがどれだけ良くデータを説明しているかの尺度です。
- incremental の R² は、その次数の多項式の R² が前の次数の多項式の R² からどれだけが増えたかの増分です。
- overall の R² は、その次数の多項式の実際の R² です。Overall R² の値が 1 に近いほど、その曲線が独立変数と従属変数の関係を良く表していることになります。独立変数の値が従属変数を殆ど予測できない場合は、R² の値が 0 に近くなります。
F 値：F 検定統計量は、独立変数が従属変数をを予測する能力の尺度です。
- incremental の F 値は、従属変数の予測に関する追加された独立変数の各次数の寄与度の増加の尺度です。次式の比であらわされます：
  
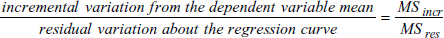
  incremental の F 値が大きく、かつ、overall の F 値が大きく跳ね上がった場合、その次数の独立変数の追加によって、従属変数の予測が前のモデルに比べて有意に改善したと結論付けることができます。多項式に使用する「最適」な次数は、一般に、予測能力を顕著に改善する最高次数の多項式です。
- Overall の F 値は、従属変数の予測に関する全ての次数の独立変数の寄与度の尺度です。次式の比であらわされます：
  
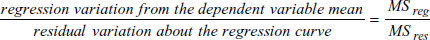
  overall の F 比が 1 前後である場合、独立変数の間に関連性はない (例えば、そのデータは「すべての標本は無作為に分布しているだけである」という帰無仮説からなっている) と結論付けることができます。
P 値：P は、F に関して算出される P 値です。P 値は、従属変数と独立変数の間に誤って関連性があると結論付ける確率です (すなわち、F に基づいて帰無仮説を誤って棄却する、すなわち、第1種の過誤 (Type I error) を犯す確率です)。P 値が小さいほど、関連性のある確率が高くなります。
- incremental の P 値は、独立変数の次数の追加で従属変数の予測が改善されることが誤りであることの確率の変化です。
- overall の P 値は、多項式の次数が従属変数を正しく予測することが誤りであることの確率です。
伝統的に P < 0.05 であれば、独立変数を従属変数の予測に使うことができると結論付けることができます。

6.3 仮説検定

Normality：正規性検定の結果には、元の母集団が回帰曲線の周囲に正規分布しているという前提条件の検定にその多項式モデルが採用されたか棄却されたか、および、その検定により算出された P 値が表示されます。この前提条件が棄却される場合は、レポートに警告が表示されます。正規性検定の棄却は、外れ値となる影響点が存在するか、あるいは、回帰モデルが誤っていることをあらわします。
Constant Variance：等分散性の検定の結果には、回帰に関する残差の等分散性の検定にその多項式モデルが採用されたか否か、および、その次数の多項式に関して算出された P 値が表示されます。すべての回帰手法では、回帰曲線に関する残差の正規分布が要求されます。

6.4 最良モデルを選択する

残差平方和と平均平方が小さいほど、その曲線は独立変数の値においてデータとより密接に適合します。一般に、使用する最良のモデルは、incremental の F 値が有意に増加している最初のモデルです。次数が上がるほど R² の値は増加することから、データを適切に説明するという観点から最も単純なモデルを採用する場合もあります。

7. 次数のみの多項式回帰の結果を解釈する

次数のみの多項式回帰のレポートには、方程式と算出されたその曲線の係数、その方程式に関する R, および R²、平均平方 (MS)、F、および P 値が表示されます。

レポートに表示されるその他の結果は、Options for Polynomial Regression ダイアログで選択します。

結果の説明

数値による結果に加えて、拡張された結果の説明が表示されることがあります。この説明テキストは、Options ダイアログボックスで有効または無効にすることができます。表示される小数点以下の桁数についても Options ダイアログボックスで指定できます。

7.1 回帰方程式

方程式とその係数の値が配置されます。方程式は次式であらあわされます：

y=b₀+b₁x¹+b₂x²+b₃x³+ … b_kx^k

ここで、y は従属変数、x は独立変数、そして、b₁, b₂, b₃ は回帰係数です。

多項式の次数は、その独立変数の指数です。観測数 N、および、欠損値があればその数も表示されます。

7.2 分散分析 (ANOVA)

MSres (残差平均平方)：平均平方は、母集団の分散の推定量です。残差平均平方は、回帰曲線に関する残差の分散の尺度で、次式で与えられます：
Rsq：決定係数 R² は、その回帰モデルがどれだけ良くデータを説明しているかの尺度です。R² の値が 1 付近であれば、その曲線は独立変数と従属変数との関係を良く説明していることを示します。R² の値が 0 付近であれば、その独立変数の値は、従属変数を予測しないことをあらわします。
F 統計量：F 検定統計量は、従属変数の予測に関してその回帰方程式がどれだけ寄与しているかの尺度です。次式の比であらわされます：

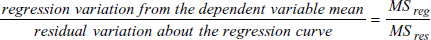
F の値が大きければ、その独立変数は従属変数の予測に寄与していると結論付けることができます (例えば、説明できないばらつき (unexplained variability) が、無作為抽出した従属変数の平均に関するばらつきの期待値より小さい場合)。F 比が 1 に近いときは、変数間には関連性がないと結論付けることができます (すなわち、このデータは、すべての標本がランダムに分布しているという帰無仮説と合致します)。
P Value：P は F に関して算出する P 値です。P 値は、従属変数と独立変数の間に誤って真の関係があると結論付ける確率です (すなわち、F に基づいて帰無仮説を誤って棄却する、すなわち、第1種の過誤 (Type I error) を犯す確率です)。P 値が小さいほど、関連性のある確率が高くなります。

7.3 推定量の標準誤差

推定量の標準誤差 (Standard Error of the Estimate) は、推定する母集団の回帰直線に関する実際の変動をあらわす尺度です。推定する母集団は、一般に観測した標本の２標準誤差の間に収まります。

PRESS Statistic：PRESS (Predicted Residual Error Sum of Squares) は、回帰モデルが新規データをどれだけ予測できるかをはかる尺度です。PRESS 統計量が小さいほど、そのモデルには予測能力があることになります。PRESS 統計量は、予測データ毎に回帰方程式の計算からその点は除外して予測誤差 (予測値と観測値の差) の二乗を合計して算出します。

7.4 Durbin-Watson 統計量

Durbin-Watson 統計量は、残差間の相関の測度です。残差間に相関がない場合、Durbin-Watson 統計量は 2 になります。この値が 2 から離れるほど、残差間の相関の尤度 (likelihood) は高くなります。この結果は、Options for Polynomial Regression ダイアログボックスでこれを選択していれば表示されます。

7.5 正規性検定

正規性検定 (Normality Test) の結果には、元になる母集団が回帰直線の周囲に正規分布しているという仮説の検定にそのデータが採択 (Passed) されたたか否か (failed)、および、この検定で算出される P 値が表示されます。いずれの回帰でも、元になる母集団は回帰直線の周囲に正規分布すると仮定されます。

正規性検定が棄却される場合は、レポートに警告が表示されます。正規性検定が棄却されるのは、外れ値となる影響点が存在するか、回帰モデルが間違っている可能性があります。

この結果は、Options for Polynomial Regression ダイアログボックスで正規性検定を無効にしない限り表示されます。

7.6 等分散検定

等分散検定 (Constant Variance Test) の結果には、元になる母集団の従属変数のばらつきが独立変数の値にかかわらず一定であるという仮説の検定にそのデータが合格 (Passed) したか否か (failed)、およびこの検定で算出される P 値が表示されます。等分散検定が棄却された場合は、レポートに警告が表示されます。

この警告が表示された場合、別のモデル (例えば、データの形状により近いモデル) の使用を検討するか、または、独立変数を変換してばらつきを安定化することでより精度の高い回帰方程式のパラメータ推定値を得ることを検討してください。

この結果は、Options for Polynomial Regression ダイアログボックスで等分散検定を無効にしない限り表示されます。

7.7 回帰診断

回帰診断の結果には Options for Polynomial Regression ダイアログボックスで選択した予測値、残差、および、その他の診断結果のみが表示されます。外れ値として評価された全ての結果には、< 記号でフラッグが付けられます。外れ値としてフラッグを付ける残差の値は、Options for Polynomial Regression ダイアログボックスで設定します。

Report Cases with Outliers Only (※) を選択していれば、単一または複数の残差に外れ値としてフラッグの付いた観測データだけがレポートされます。その観測データのその他の結果は全て表示されます。(※ v14 では Report flagged values only)

Row (行)：これは、測定データの行番号です。
Residuals (残差)：生の残差で、従属変数に関する測定値と予測値の差です。
Standardized Residuals (標準化残差)：標準化残差 (Standardized Residuals) は、生の残差を推定量の標準誤差 s_y|x で割ったものです。この残差が回帰モデルの周囲に正規分布していれば、標準化残差の約 66% は、-1 から +1 の間の値をとり、標準化残差の約 95% は、-2 から +2 の間の値をとります。標準化残差の値が大きいほど、その点は回帰モデルから離れていることを示します。外れ値としてフラッグを立てる値は、2.5 が提示されます。

7.8 信頼区間

これらの結果は、Options for Polynomial Regression ダイアログボックスで選択している場合に表示されます。信頼区間にゼロが含まれていなければ、指定した信頼水準でその係数はゼロではないと結論付けることができます。これは、 P < α (alpha) としても表現できます。ここで、α は、係数はゼロではないと誤って結論付けてもよしとする確率で、信頼区間は 100(1 – α) となります。

信頼水準は、1 から 99 までの任意の値を指定できます。提示される信頼水準はいずれの区間についても 95% です。

Row (行) ：これは、測定データの行番号です。
Predicted (予測値) ：この列は回帰モデルによって予測される測定データ毎の従属変数の値です。
Regression：回帰直線の信頼区間では、指定した信頼水準について従属変数と独立変数との間の真の関係を含む領域を計算した変数の値の範囲が表示されます。この結果は、Options for Polynomial Regression で選択した場合に表示されます。信頼水準には 1 から 99 の間の任意の値を指定できます。提示される信頼水準は 95% です。
Population Confidence Interval：指定した信頼水準について観測データを抽出した母集団を含む領域を定める値です。この結果は、Options for Polynomial Regression ダイアログボックスでこれを選択している場合に表示されます。信頼水準には 1 から 99 の間の任意の値を指定できます。提示される信頼水準は 95% です。

8. 多項式回帰のレポートグラフ

多項式回帰の結果を使用して、以下に示す最大５つのグラフを作成することができます：

残差のヒストグラム (Histogram of Residuals)：詳しくは、残差のヒストグラム (Histogram of Residuals) をご覧ください。
残差の散布図 (Scatter plot of the residuals)：詳しくは、残差の散布図 (Scatter Plot of the Residuals) をご覧ください。
標準化残差の棒グラフ (Bar Chart of the Standardized Residuals)：詳しくは、標準化残差の棒グラフ (Bar Chart of the Standardized Residuals) をご覧ください。
残差の正規確率プロット (Normal probability plot of the residuals)：詳しくは、正規確率プロット (Normal Probability Plot) をご覧ください。
１独立変数の回帰変数と信頼および予測区間の折れ線/散布図 (Line/scatter plot of the regression variable and confidence and prediction intervals with one independent)：詳しくは、予測および信頼区間付き 2D 回帰直線と散布図 (2D Line/Scatter Plots of the Regressions with Prediction and Confidence Intervals) をご覧ください。

8.1 多項式回帰のレポートグラフを作成する

多項式回帰レポートデータのレポートグラフを作成するには：

Polynomial Regression レポートを表示して、Report タブをクリックします。
Result Graphs グループにある Create Result Graph をクリックします。Create Result Graph ダイアログボックスに Polynomial Regression の結果で使用できるグラフのタイプが表示されます。
Graph Type リストから作成したいグラフのタイプを選択して、OK をクリックするか、リストから作成したいグラフをダブルクリックします。
選択したグラフがグラフウィンドウに表示されます。詳しくは、レポートグラフをご覧ください。