23.4 多重ロジスティック回帰

多重ロジスティック回帰 (Multiple Logistic Regression) は、データにロジスティック関数をあてはめることによって、単一または複数の独立変数の観測データから、例えば、疾病の有り/無しといった、定性的な従属変数を予測したいときに使います。

独立変数は、予測変数とも呼ばれる既知の変数です。独立変数を変化させると、それに対応する従属変数 (すなわち応答変数) の値が決まります。SigmaPlot のロジスティック回帰では、従属変数が２値 (dichotomous) であること、すなわち、応答のとりうる値 (生か死か、黒か白か) が 0 と 1 の２つの値であらわされる必要があります。

お持ちのデータの従属変数が２値でない場合、独立変数が１つであれば単純線形回帰 (Simple Linear Regression) を、独立変数が複数あれば多重線形回帰 (Multiple Linear Regression) 使います。

多重ロジスティック回帰について
多重ロジスティック回帰を実行する
多重ロジスティック回帰のデータを配置する
多重ロジスティック回帰オプションを設定する
多重ロジスティック回帰を実行する
多重ロジスティック回帰の結果を解釈する

1. 多重ロジスティック回帰について

多重ロジスティック回帰 (Multiple Logistic Regression) では、従属変数と k 個の独立変数との関係が以下の多次元平面であらわされる一般方程式に当てはめられることが仮定されます：

ここで、y は従属変数、P(y =1) は従属変数が正の応答、すなわち値が 1 となる予測確率、b₀ から b_k は k+1 個の回帰係数、そして、x₁ から x_k は独立変数となります。

x_i の値を変化させると、それに対応する y =1 となる予測確率も、関連する回帰係数 b_i の符号に応じて増加または減少します。

多重ロジスティック回帰では、与えられた独立変数の観測値から従属変数の観測値を最も良く予測する回帰係数の値の集合を求めます。

2. 多重ロジスティック回帰を実行する

多重ロジスティック回帰を実行するには：

ワークシートに適切なデータを入力または配置します。詳しくは、多重ロジスティック回帰のデータを配置するをご覧ください。
Logistic Regression オプションを設定します。
Analysis タブをクリックします。
SigmaStat グループにある Tests ドロップダウンリストから以下を選択します：Regression → Multiple Logistic
Multiple Logistic Regression レポートを表示して内容を解釈します。詳しくは、多重ロジスティック回帰の結果を解釈するをご覧ください。
検定を実行します。

3. 多重ロジスティック回帰のデータを配置する

測定された従属変数のデータを１列に、それに対応する独立変数のデータを２列目以降の列に配置します。

ロジスティック回帰データは、観測された従属変数のデータを１列に、対応する独立変数のデータをそれ以外の単一または複数の列に配置する生データ (raw data) フォーマットでワークシートに入力します。従属変数のデータは２値データとして、独立変数のデータは数値形式で入力する必要があります。

お持ちの従属変数データが、連続する数値データであったりテキストである場合、または、カテゴリ型の独立変数を使用している場合は、参照コーディングを使ってそれらを同等のダミー変数の集合に変換する必要があります。

欠損値を含む観測データは無視されます。また、いずれの列も長さを等しくする必要があります。

4. 多重ロジスティック回帰オプションを設定する

多重ロジスティック回帰 (Multiple Logistic Regression) オプションを使うのは：

ロジスティック回帰方程式がデータにどれだけうまく当てはまっているかを判定するのに使用するオプションを設定するとき。
回帰係数の VIF (variance inflation factors) を推定するとき。
残差の表示とワークシートへの保存を設定するとき。
係数の標準誤差 (Standard Error Coefficients)、ワルド統計量 (Wald Statistic)、オッズ比 (Odds Ratio)、オッズ比の信頼区間 (Odds Confidence Interval)、および、係数の P 値 (Coefficients P Values) を計算するとき。
データポイントの外れ値や影響度を識別する検定を指定するとき。

多重ロジスティック回帰オプションを変更するには：

検定オプションの変更後に検定を実行するに際して、検定の実行前にデータを選択しておきたい場合は、対象とするデータ列をポインターでドラッグしておきます。
Analysis タブを選択します。
SigmaStat グループの Tests ドロップダウンリストから Multiple Logistic Regression を選択します。
Options をクリックします。Options for Multiple Logistic Regression ダイアログボックスに以下の３つのタブが表示されます：
1. Criterion：Criterion タブをクリックすると、各種判定基準のオプションが表示されます。詳しくは、Options for Multiple Logistic Regression: Criterion をご覧ください。
2. More Statistics：More Statistics タブをクリックすると、Standard Error Coefficients、Wald Statistic, Odds Ratio, Odds Ratio Confidence, and Coefficients P Values, Predicted Values, and Variance Inflation Factor オプションが表示されます。詳しくは、Options for Multiple Logistic Regression: More Statistics をご覧ください。
3. Residuals：Residuals タブをクリックすると、残差 (Residuals) と影響力 (Influence) オプションが表示されます。詳しくは、Options for Multiple Logistic Regression: Residuals をご覧ください。SigmaPlot を次回以降起動するときは、ここで選択したオプションの内容が保持されます。
検定を続行するには、Run Test をクリックします。
現在の設定内容を適用して、オプションダイアログを閉じるには、OK をクリックします。

4.1 Options for Multiple Logistic Regression: Criterion

各種判定基準のオプションを設定するには、Options for Multiple Logistic Regression ダイアログボックスの Criterion タブをクリックします。これらのオプションを使って、ロジスティック方程式とデータの当てはまりの良さを検定する判定基準を指定します。

Hosmer-Lemshow Test Statistic：Hosmer-Lemshow 統計量は、そのロジスティック方程式はデータに適合しているという帰無仮説を、それぞれの結果 (outcome) の個体数とロジスティック方程式に基づく期待値とを比較することによって検定します。
- Threshold probability for goodness of fit：P 値が小さいと、ロジスティック方程式がデータに適合するという帰無仮説が棄却されることになり、独立変数を変えて方程式を試みることになります。P 値が大きいと、そのロジスティック方程式とデータの当てはまりは良いと示されることになります。デフォルトの値は 0.2 です。P 値を大きい値に設定すると、ロジスティック方程式による予測値と従属変数の観測値との偏差が小さくなければ、方程式とデータの当てはまりが良いことを採用できません。P 値を変更するには、編集ボックスに別の値を入力します。
Pearson Chi-Square Statistic：ピアソンのカイ二乗統計量は、ピアソン残差 (Pearson residuals) の二乗を合計することによってロジスティック方程式のデータに対する適合度を検定します。Pearson Chi-Square statistic の値が小さければ、ロジスティック方程式とデータの適合が良いことを示します。この値が大きければ、適合が悪いことを示します。
Likelihood Ratio Test Statistic：尤度比検定統計量は、逸脱残差 (deviance residuals) の二乗を合計することによってロジスティック方程式のデータに対する適合度を検定します。ここでは、モデル全体と従属変数の平均値だけを使用したモデルを比較します。P 値が小さければ、ロジスティック方程式とデータの適合が良いことを示します。
Classification Table：分類表は、そのデータがロジスティック方程式に従うという帰無仮説を、それぞれの結果 (outcome) の個体数とロジスティック方程式に基づく期待値とを比較することによって検定します。データがロジスティック方程式に適合しているか否かが、従属変数の実際の応答と予測応答を交差分類し、独立変数の異なる組み合わせの数を特定することによって要約されます。
- Threshold probability for positive classification：予測応答には、推測するロジスティック確率と Threshold probability for positive classification 編集ボックスで指定した確率値とを比較して導かれる二値変数が割り当てられます。予測確率が指定した確率値を上回る場合は、予測値に正の応答 (値 1) が割り当てられます。推測確率が指定した値と等しいか小さい場合は、ゼロまたは基準値 (reference value) が割り当てられます。デフォルトの閾値は 0.5 です。作成された分割表は、カイ二乗検定を使って分析します。Hosmer-Lemshow 統計量と同様、P 値が大きければ、そのロジスティック方程式とデータの当てはまりは良いと示されることになります。詳しくは、多重ロジスティック回帰の結果を解釈するをご覧ください。
Number of Independent Variable Combinations：独立変数の唯一の組み合わせの数が独立変数の数と比較して大きくない場合、そのロジスティック回帰は信頼できないものであるという結果になります。独立変数の組み合わせの数を計算し、独立変数と比較して十分な組み合わせの数が無ければ警告を表示させるには、Number of Independent Variable Combinations チェックボックスを選択します。計算された独立変数の組み合わせが該当する編集ボックスの値より小さければ、独立変数の組み合わせの数が小さすぎるとの警告と、継続するか否かを尋ねるダイアログボックスが表示されます。Yes を選択すると、レポートに警告メッセージが表示されます。

4.2 Options for Multiple Logistic Regression: More Statistics

Standard Error Coefficients：Standard Error Coefficients (係数の標準誤差) は、回帰係数の見積もりの精度の尺度です。推定する母集団の真の回帰係数は、一般に観測した標本の係数の２標準誤差の範囲に収まります。
Wald Statistic：ワルド統計量は、推測する係数の観測値とその標準誤差を比較します。次式の比で算出されます：

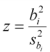
ここで、b_i は推測する係数の観測値、s_{b_i} はその係数の標準誤差です。

Wald Statistic を選択すると、係数の測定値とその標準誤差の比がレポートに追加されます。ワルド統計量は、その独立変数が従属変数の予測においてどれだけ有意であるかを判定するのに使用することもできます。
Odds Ratio：任意の事象が起こるオッズは次式で定義できます：

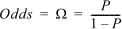
ここで、P は事象が発生する確率です。独立変数のオッズ比は次式で計算します：

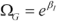
ここで β_I は回帰係数です。オッズ比は、独立変数が 1 増加したときに、結果のオッズがどれだけ増加 (または減少) するかをあらわす推定量です。
Odds Ratio Confidence：オッズ比の信頼区間は、次式で定義されます：

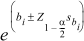
ここで、b_i は係数、s_{b_i} はその係数の標準誤差です。また、

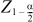
は、目的とする信頼区間に対応する標準正規分布の軸上の点です。

デフォルトで使用する信頼区間は 95% です。使用する信頼区間を変更するには、該当する編集ボックスのパーセントの値を変更します。
Coefficients P Value：Coefficients P Value (係数の P 値) は、各従属変数の決定に関してそれぞれの独立変数に有意な効果があると誤って結論付けてしまう確率を決定します。P 値が小さいほど、その独立変数が実際に従属変数を予測する可能性は高くなります。Wald Statistic を使えば、独立変数に関連する係数がゼロから有意な差があるか否かが検定されます。独立変数の有意性は、その係数の観測値と関連する係数の標準誤差を比較することによって検定します。係数の観測値がその標準誤差と比べて大きければ、その係数はゼロから有意な差があるので、その独立変数による従属変数の予測の寄与は有意であると結論付けることができます。詳しくは、多重ロジスティック回帰の結果を解釈するをご覧ください。

Predicted Values：このオプションを使えば、独立変数の観測値ごとに従属変数の予測値を計算し、その結果をワークシートに保存します。ロジスティック回帰では、正の応答の確率が予測値で示されます。詳しくは、多重ロジスティック回帰の結果を解釈するをご覧ください。予測値をワークシートの列に配置するには、予測値を保存したいワークシートの列を該当するドロップダウンリストから選択します。Predicted Values のチェックボックスを選択して none を選択すると、その値はレポートには表示されますが、ワークシートにデータは配置されません。
Variance Inflation Factor：このオプションを使用すると、独立変数の多重共線性 (multicollinearity)、すなわち、当てはめにおける独立変数の線形結合が測定されます。回帰プロシージャーでは、独立変数は統計的に互いに独立であること、例えば、ある独立変数の値は他の独立変数の値に影響を及ぼすことはないことが仮定されます。しかし、このような理想的な状況が現実の世界でおこるのは希です。独立変数が互いに相関関係にある場合、すなわち、冗長な情報が含まれている場合、その回帰モデルのパラメータ推定量は、信頼できないものになる可能性があります。回帰モデルのパラメーターは、従属変数を予測する独立変数の理論的に唯一の寄与度をそれぞれ数値化します。もし、独立変数が相関関係にあれば、それらの間には何らかの共通情報が含まれていることになりますので、パラメータ推定量が「汚染」されていることになります。もし、多重共線性が深刻なものであれば、そのパラメーター推定量は信頼できないものになります。多重共線性には以下の２つのタイプがあります。
- Sample-Based Multicollinearity (標本に基づく多重共線性)：標本に基づく多重共線性が生じるのは、独立変数が相関するような方法で標本となる観測データが収集されている場合です (例えば、年齢の異なる児童に関して年齢、身長、および、体重を収集したとすれば、各変数の間には互いに相関関係があります)。
- Structural Multicollinearity (構造的多重共線性)：構造的多重共線性が生じるのは、回帰方程式に互いに影響を及ぼしあう複数の独立変数が含まれている場合です。構造的多重共線性が生じる最も一般的な形式は、多項式回帰方程式の独立変数が幾つかの累乗 (power) になっている場合です。このような累乗 (例えば、x, x², … など) には互いに相関関係があるので構造的多重共線性が生じます。回帰方程式に交互作用項を含める場合も、構造的多重共線性が生じることがあります。
- Flag values >：Flag Values > 編集ボックスの値を多重共線性変数の閾値として使います。デフォルトの閾値は 4.0 で、これは、4.0 より大きい値はいずれも多重共線性としてフラッグが付くことを意味します。この多重共線性の検出をより敏感にするには、この値を小さくします。そのデータに多重共線性があるというフラッグが付く前に、独立変数の相関関係を許容する範囲を広げるには、この値を大きくします。詳しくは、多重共線性の対処法をご覧ください。VIF ( variance inflation factor) が大きければ、その回帰モデルに余分な変数が存在することになり、パラメータ推定値が信頼できないものになります。VIF ( variance inflation factor) の値が 4 より大きければ、多重共線性の可能性が提示されます。この値が 10 より大きければ、多重共線性が深刻であることをあらわします。
Report Flagged Values Only (フラッグを立てた値のみレポートする) ：影響力ポイント検定でフラッグが立てられた影響力のポイントだけをレポートに含める場合は、Report Flagged Values Only を選択します。このオプションを解除すると影響力のある全てのポイントがレポートに含まれることになります。

4.2.1 多重共線性の対処法

標本に基づく多重共線性 (Sample-based multicollinearity) は、他の条件下でデータを多く収集して独立変数間の相関関係を無くすことで解消される場合があります。もし解消できなければ、その回帰方程式のパラメーターは過剰であることになり、単一または複数の独立変数を取り除くことで多重共線性を排除する必要があります。

構造的多重共線性 (structural multicollinearities) は、累乗や交互作用項ができる前に独立変数を中心化することによって解消することができます。

4.3 Options for Multiple Logistic Regression: Residuals

オプションダイアログボックスの Residuals タブをクリックすると、Residual Type, Raw, Standardized, Studentized, Studentized Deleted, および Report Flagged Values Only オプションが表示されます。

Residual Type：残差はデフォルトではレポートされません。レポートに残差を含めるには、Residual Type ドロップダウンリストから Pearson または Deviance を選択します。レポートに残差を含めたくない場合は、ドロップダウンリストから None を選択します。
- Deviance (逸脱) 残差は、ロジスティック方程式のデータに対する全適合度を検定する尤度比検定統計量 (Likelihood Ratio Test Statistic) の計算に使用します。尤度比検定統計量は、逸脱残差の二乗の合計です。各点の逸脱残差は、その点が尤度比検定統計量にどれだけ寄与しているかをはかる尺度です。逸脱残差の値が大きいほど、従属変数の観測値と予測値の間の差が大きいことを示します。
- Pearson (ピアソン) 残差は、生の残差を標準誤差で割って求めたものです。標準誤差は、従属変数の観測値 (0 または 1) をロジスティック回帰方程式で推測した正の応答 (例えば y=1) となる確率で割ったものとして定義されます。カイ二乗適合度検定量がピアソン残差を二乗した合計であることから、ロジスティック方程式の適合度の計算では、ピアソン残差をデフォルトの残差タイプとして使用します。
Raw Residuals：生の残差とは、従属変数の予測値と観測値との差です。レポートに生の残差を含めるには、このチェックボックスを選択します。生の残差をワークシートに含めたくなければ、このチェックボックスを解除してください。生の残差をワークシートの列に配置するには、該当するドロップダウンリストから配置したい列の番号を選択します。Raw チェックボックスを選択した状態でドロップダウンリストに none を選択すると、レポートにはその値が表示されますが、ワークシートには配置されません。
Studentized Residuals：スチューデント化残差は、データの両極値に対する中央付近の回帰直線の精度の高さを考慮に入れることによって残差を基準化するものです。スチューデント化残差は、スチューデントの t 分布に従う傾向がありますので、t 分布を利用してスチューデント化残差の大きい値を決定することができます。SigmaPlot は、例えば、データポイントの中心から外れたデータポイントに対しては、スチューデント化残差の値が「大きい」というフラッグを自動的に立てます。フラッグで提示されるデータポイントは、回帰母集団の95％信頼区間の外側にあります。レポートにスチューデント化残差を含めるには、Studentized チェックボックスが選択されていることを確認してください。スチューデント化残差をワークシートに含めたくない場合は、選択されたチェックボックスをクリックしてください。
Studentized Deleted Residuals：スチューデント化削除残差は、スチューデント化残差に似ていますが、該当するデータポイントを使わずに、回帰方程式を計算することで値を求める点が異なります。スチューデント化削除残差をレポートに含めるには、このチェックボックスが選択されているかを確認してください。スチューデント化削除残差をワークシートに含めたくなければ、選択されたチェックボックスをクリックします。SigmaPlot は、例えば、データポイントの中心から外れたデータポイントに対しては、スチューデント化削除残差の値が「大きい」というフラッグを自動的に立てます。フラッグで提示されるデータポイントは、回帰母集団の95％信頼区間の外側にあります。

※ Note：スチューデント化残差、および、スチューデント化削除残差はいずれも、同じ信頼区間の設定を使って外れ値を判定します。
Report Flagged Values Only (フラッグ値のみレポートする)：レポートにフラッグの立てられた標準、および、スチューデント化削除残差しか含めない場合は、Report Flagged Values Only を選択してください。このオプションを解除すると、標準残差およびスチューデント化残差のすべてがレポートに含まれます。

Influence オプションは、影響力のあるデータポイントのインスタンスを自動的に検出するものです。影響力がもっとも強いポイントは、データポイントの外れ値です。すなわち、それ以外のデータポイントと一直線上に並ぼうとはしないものです。これらの点は、回帰直線の計算において極端に強い影響を及ぼす可能性があります。影響力のあるポイントを識別し定量化するための影響力の検定には、幾つかの種類が用意されています。

Leverage：回帰方程式の結果に影響を及ぼすポイントである可能性があるかを識別するには Leverage を選択します。てこ比は、独立変数の値にのみ依存します。てこ比の高い観測データは、独立変数の極値 (大きい値と小さい値) になる傾向があります。このような点では、独立変数のわずかな変化が従属変数の予測値に大きく影響を及ぼす可能性があります。データポイントのてこ比の期待値は次式であらわされます：

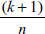
ここで、k は独立変数の数、n はデータポイントの数です。観測データのレバレッジが期待されるレバレッジより大きい場合は、その点に影響力がある疑いがあります。

Leverage を選択すると、ポイント毎のてこ比を計算し、影響力の疑いのある点、例えば、期待されるてこ比が指定した倍数より大きいものであれば自動的にフラッグが付けられます。提示される値は、その回帰に期待されるてこ比の 2.0 倍です。例えば、

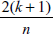
影響力の疑いがある点として余分なフラッグを立てないようにするには、この値を高くします。影響力の小さなポイントにフラッグを立てるには、この値を低くします。
Cook’s Distance (クックの距離)：クックの距離は、回帰方程式のパラメータ推定値に対して各ポイントの影響力がいかに大きいかを測る尺度です。クックの距離は、ある点を分析から除外したときに回帰係数の値がどれだけ変化するかを評価します。クックの距離は、独立変数と従属変数の両方の値に依存します。全てのポイントに対してこの値を計算し、影響力のあるポイント、例えば、指定値よりもクックの距離の値が大きいポイントに対してフラッグを立てるようにするには、Cook’s Distance を選択します。提示される値は 4.0 です。クックの距離が 1 より大きければ、その点に影響力が存在する可能性があることを示します。クックの距離が 4 より大きければ、その点はパラメータの推定値に対して大きな影響力があることを示します。影響力のある点として余分なフラッグを立てないようにするには、この値を高くします。影響力の小さなポイントにフラッグを立てるには、この値を低くします。詳しくは、影響点の対処法をご覧ください。

4.3.1 影響点の対処法

影響点には次の２つの原因があります：

観測データやデータ入力のエラーによってそのデータポイントに何らかの瑕疵が生じている場合。
モデル自体に誤りがある場合。

データの収集や入力に誤りがあった場合は、その値を修正してください。修正する値がわからなければ、そのデータポイントの削除を判断できるかもしれません。モデルに誤りがあるようであれば、回帰の独立変数を変更するか、非線形回帰をお試しください。

5. 多重ロジスティック回帰を実行する

多重ロジスティック回帰 ( Multiple Logistic Regression) を実行するには、検定するデータを選択する必要があります。検定ウィザードの Select Data パネルを使用して、検定したいデータを含むワークシートの列を選択します。

多重ロジスティック回帰を実行するには：

検定を実行する前にデータを選択したい場合は、データ範囲をマウスポインタでドラッグしておきます。
Analysis タブをクリックします。
SigmaStat グループの Tests ドロップダウンリストから以下を選択します：Regression → Multiple Logistic検定ウィザードの Select Data パネルが表示されます。検定を選択する前に列を選択していれば、Selected Columns リストにその列が表示されます。列を選択していなければ、データ選択の指示がダイアログボックスに表示されます。
Selected Columns リストに別のワークシート列を割り当てたい場合には、ワークシートで直接その列を選択するか、Data for Dependent または Data for Independent ドロップダウンリストからその列を選択します。
Selected Columns リストの Dependent 行に割り当てられるのは最初に選択した列で、リストの Independent 行に２列目以降が割り当てられます。
値を含む列を選択すると、dependent と independent の組合せを繰り返す回数が表示されます。各行には、選択した列の番号またはタイトルが表示されます。
選択した内容を変更するには、リストの割り当てを選択したあと、ワークシートから列を選択しなおします。Selected Columns リストの内容をダブルクリックすることによって、列の割り当てを消去することもできます。
Finish をクリックすると、回帰が実行されます。正規性と等分散性、残差の独立性を検定するよう指定している場合、SigmaPlot は、正規性 (Shapiro-Wilk または Kolmogorov-Smirnov)、等分散性、残差の独立性を検定します。もしデータに関するこれらの検定のいずれかが棄却されると、SigmaPlot によりその旨が報告されます。検定が完了すると、Multiple Logistic Regression の結果をあらわすレポートが表示されます。残差 (Residual) とその他の結果をワークシートに配置するよう選択している場合は、指定した列にそれらが配置され、それぞれラベルが付けられます。

6. 多重ロジスティック回帰の結果を解釈する

多重ロジスティック回帰のレポートには、方程式と算出された係数、それらの標準誤差、検定の観測データの数、ロジスティック方程式をデータに当てはめるのに使用した推定基準、従属変数データのあるワークシートの列、正の応答と参照応答をあらわす値、および、Hosmer-Lemshow およびカイ二乗適合度の統計量が表示されます。

レポートに表示されるその他の結果は、Options for Linear Regression ダイアログボックスで有効または無効にすることができます。

結果の説明

数値による結果に加えて、拡張された結果の説明が表示されることがあります。この説明テキストは、Options ダイアログボックスで有効または無効にすることができます。表示される小数点以下の桁数についても Options ダイアログボックスで指定できます。

6.1 回帰方程式

ロジスティック回帰方程式は次式で与えられます：

ここで、P は「正 (Positive)」の応答 (例えば、従属変数の値が 1 ) の確率、x₁, x₂, x₃, …, x_k は独立変数、b₁, b₂, b₃,…, b_k は回帰係数です。この方程式は、両辺にロジット変換を適用して次式に書き換えることができます。

6.2 観測数

観測データの数 N。欠損値を含む観測データの数は回帰分析から除外されますが、これも表示されます。

6.3 推定基準 (Estimation Criterion)

ロジスティック回帰では、最尤法 (maximum likelihood approach) を使用して、観測データに最も良く適合していそうなロジスティック回帰方程式の係数 (b_i ) の値を求めます。

※ Note：多重ロジスティック回帰の残差の平方和を最小化して算出する回帰係数も最尤推定量です。

6.4 従属変数

レポートの Dependent Variable セクションには、従属変数列のどの値が正の応答 (1) をあらわし、どの値が参照応答 (0) をあらわすかが示されます。

6.5 独立変数の固有の組合せの数

Number of Unique Independent Variable Combinations の値は、独立変数の固有の組合せの数をあらわします。Options for Logistic Regression ダイアログボックスの Number of Independent Variable Combinations オプションを選択している場合に表示されます。独立変数の固有の組合せの数は、実際の独立変数の数と比較されます。もしこの値が Number of Independent Variable Combinations オプションで指定した値よりも小さければ、その結果は信頼できないものである可能性があるとの警告メッセージがレポートに表示されます。

6.6 Hosmer-Lemshow の P 値

Hosmer-Lemshow の P 値は、それぞれの結果 (outcome) の個体数とロジスティック方程式に基づく期待値とを比較することによってそのロジスティック回帰方程式のデータに対する適合度を示します。検定する帰無仮説は、「そのロジスティック方程式はデータをあらわす」です。したがって、P 値が小さければ、その方程式はデータと当てはまりが悪いことになります (例えば、一致するという帰無仮説を棄却します)。P 値が大きければ、そのロジスティック方程式とデータの当てはまりは良いことになります。Hosmer-Lemshow の P 値の臨界点は、Options for Multiple Logistic Regression ダイアログボックスで設定します。

データセットが少ない場合、ロジスティック回帰を測定する適合度の解釈には細心の注意を払ってください。いずれの P 値もカイ二乗確率分布に基づくものですが、これは観測データが少ない場合の使用は推奨されていないからです。

6.7 ピアソンのカイ二乗統計量

Pearson Chi-Square statistic (ピアソンのカイ二乗統計量) は、ピアソン残差を二乗して合計したものです。これは、カイ二乗検定統計量を使用して従属変数の観測値と予測値との一致度をはかる尺度です。カイ二乗検定統計量は、通常の線形回帰における残差平方和と同等のものです。カイ二乗の値が小さければ (およびそれに対応する P 値が大きければ) 、そのロジスティック回帰方程式とデータの適合度が良いことを示し、カイ二乗の値が大きければ (およびその P 値が小さければ)、適合度が悪いことを示します。ピアソンのカイ二乗オプションは、Options for Multiple Logistic Regression ダイアログボックスで設定します。

6.8 尤度比検定統計量

Likelihood Ratio Test Statistic (尤度比検定統計量) は、逸脱残差 (deviance residuals) の二乗を合計して求めたものです。独立変数の従属変数に対する影響がない観測データを得る見込みと、独立変数の従属変数に対する影響がある観測データを得る見込みを比較することによって、そのロジスティック方程式のデータに対する適合度を示します。

この比較は、その独立変数を使う場合と使わない場合のロジスティック回帰を実行し、それらの結果を比較することによって算出されます。もし、独立変数が結果に影響を及ぼすパターンが及ぼさないパターンと比べて多く生じる結果が観測されれば、レポートされる P 値の率は小さくなり、そのことはロジスティック回帰方程式とデータの適合度が良いことを示します。

6.9 対数尤度統計量

-2 対数尤度 (-2*Log(Likelihood)) 統計量は、実際の観測値と予測確率との間の適合度の尺度です。次式の和で与えられます：

ここで、y_i と μ_i は、それぞれ、従属変数の観測値と予測値、n は観測データの数です。なお、ln(1) はゼロなので観測値は必ず 0 か 1 になる点に注意してください。したがって、予測値が観測値に近いほど、この和はゼロに近づくことになります。

また、-2 対数尤度は、逸脱残差 (deviance residuals) の二乗の合計とも等しくなります。

-2 対数尤度 (LL) 統計量と尤度比 (LR) は、次式の関係にあります：

LR = LL – LL₀

ここで、LL₀ は、独立変数をもたない定数項のみからなる回帰モデルの -2 対数尤度です。この関係から、LL₀ と LL はいずれも正であるので、適合度が高いほど LL は必ずゼロに近づく点に注意してください (極端な場合、完全に適合していれば LL はゼロになり、全く適合していなければ LL は LL₀ と等しくなります)。したがって、LR が大きいほど与えられた従属変数に関する独立変数の暗黙の説明力は大きいことになります。

6.10 正に分類する確率の閾値

この確率の閾値は、ロジスティックモデルによって予測される分類表と確率表 (下記参照) の応答が正 (positive) または参照 (reference) のいずれになるかを決定します。指定した予測値の閾値より、確率表の予測確率が上回れば、その予測値には正の応答 (値 1) が割り当てられます。反対に、指定した値より小さいか等しい確率であれば、値 0 または参照値が割り当てられます。この閾値確率は、Options ダイアログボックスで設定します。

6.11 分類表

分類表 (Classification Table) は、観測された従属変数の応答と予測された従属変数の応答を交差分類し、正しく分類されたケースと誤って分類されたケースを識別し、その数の結果をまとめたものです。

ロジスティックモデルによって分類される応答は、確率表の推定ロジスティック確率と、指定した確率の閾値を比較することによって求められます (前のセクションを参照)。

この表は、Options ダイアログボックスの Classification Table オプションを選択したときにレポートに表示されます。

6.12 確率表

確率表 (Probability Table) には、従属変数の実際の応答と、正の応答 (値 1) の予測ロジスティック確率、および、従属変数の予測応答がリストされます。予測応答には、予測ロジスティック確率と指定した確率の閾値を比較して求めた 1 (正の応答) か 0 (参照応答) の値が割り当てられます (前のセクションを参照)。

この表は、Options ダイアログの Predicted Values オプションを選択したときにレポートに表示されます。

6.13 統計サマリー表

このサマリー表には、係数、標準誤差、Wald 統計量、オッズ比、オッズ比の信頼区間、P 値、および独立変数の VIF がリストされます。

Coefficients：回帰モデルの constant (定数) と独立変数の係数の値がリストされます。
Standard Error：回帰係数の標準誤差です (平均の標準誤差に相当します)。推測する母集団の真の回帰係数は、一般に観測された標本の係数のおよそ２標準誤差の範囲に収まります。標準誤差が大きいと多重共線性の疑いがあります。これらの値を使ってワルド統計量と回帰係数の信頼区間を算出します。
Wald Statistic：ワルド統計量は、回帰係数を標準誤差で割ったものです。次式の比で算出されます：

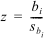
ここで、z は Wald 統計量、b_i は推測する係数の測定値、s_{b_i} はその係数の標準誤差です。
P 値： P は、Wald 統計量に関する P 値を計算したものです。P 値は、変数間に真の関係性があると誤って結論付ける確率です。P 値は自由度 1 のカイ二乗分布に基づきます。P 値が小さいほど、その独立変数が従属変数に影響を及ぼす確率は高くなります。伝統的に P < 0.05 であれば、その独立変数が従属変数の予測に寄与すると結論付けることができます。
Odds Ratio：独立変数のオッズ比は次式で計算します：

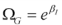
ここで β_I は回帰係数です。オッズ比は、独立変数が 1 増加したときに、結果のオッズがどれだけ増加 (または減少) するかをあらわす推定量です。
Odds Ratio Confidence (オッズ比の信頼区間)：これら２つの値は、真のオッズ比が存在する信頼区間の加減と上限をあらわします。この信頼水準 (95%) は、オプションダイアログで設定します。
VIF (Variance Inflation Factor)：VIF (Variance Inflation Factor) は、多重共線性の尺度です。ある独立変数の回帰パラメーター (係数) の標準誤差が、それ以外の独立変数の余計な情報によって「ふくらむ (inflation)」かを測定します。VIF が 1.0 の場合、他の独立変数には余計な情報が無いことになります。VIF が非常に大きければ、その回帰モデルに余計な変数が存在することになり、そのパラメーターの推定値は信頼できないものになります。独立変数の VIF の値が指定した値より大きければ、他の独立変数に多重共線性があることを示す > 記号のフラッグが付きます。多重共線性が深刻である場合、回帰方程式に余計な独立変数が多く存在することを示します。回帰方程式の品質を改善するには、余計な変数を削除する必要があります。多重共線性のフラッグをつけるカットオフ値は Options ダイアログボックスで設定します。提示される値は 4.0 です。

6.14 残差の計算方法

Residual calculation method には、ロジスティック回帰を計算した残差が表示されます。この残差は、Options for Logistic Regression ダイアログで Pearson (ピアソン) または Deviance (逸脱度) を選択することができます。選択した内容によって、逸脱残差 (deviance residual) の二乗を最小化するロジスティック回帰それ自体には影響しませんが、スチューデント化残差の計算には影響します。

ピアソン残差は次式で定義されます：

ここで、 y_i と μ_i は、それぞれ、i 番目のケースの従属変数の観測値と予測値です。

逸脱残差 (deviance residual) は次式で定義されます：

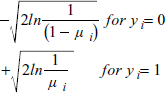
6.15 残差表

残差表には、オプションダイアログボックスの関連オプションの選択に応じて、生の残差、ピアソンまたは逸脱残差、スチューデント化、および、スチューデント化削除残差が表示されます。外れ値として判断された全ての残差には < 記号のフラッグが付きます。外れ値としてフラッグをつける残差のトリガーとなる値も、Options for Multiple Logistic Regression ダイアログで設定します。

Report Flagged Values Only を選択していれば、単一または複数の残差に外れ値としてフラッグの付いた観測データのみがレポートに表示されます。ただし、その観測データに関するそれ以外の結果は全て表示されます。残差の計算方法は、オプションダイアログボックスの残差タイプに Pearson を選択したか Deviance を選択したかに応じて変わります。

Row：観測データの行番号です。なお、データに欠損値が含まれている場合、該当する行はいずれも残差表から除外されます。
Pearson/Deviance Residuals：残差表には、Options for Logistic Regression ダイアログボックスの Residual Type オプションで設定した内容に応じて、Pearson または Deviance 残差のいずれかが表示されます。ピアソン残差と逸脱残差のいずれも、ロジスティック方程式とデータとの間の適合度をあらわし、その値が小さいほど適合度が良いことを示します。これら２つの残差タイプは計算手法が異なり、この表のスチューデント化残差の計算に影響します。ピアソン残差は、標準化残差 (standardized residuals) としても知られていますが、生の残差を標準誤差で割ったものです。逸脱残差 (Deviance residuals) は、最大尤度プロシージャーの一部として最小化する尤度関数に各点がどれだけ寄与するかを測定したものです。
Raw Residuals：生の残差は、被験者やケースそれぞれの予測値と観測値との差です。
Studentized Residuals：スチューデント化残差は、データセットの「中央」の従属変数の予測値により大きな寄与があることを考慮に入れた標準化残差です。この残差は、推測する標準誤差を全てのデータを使って計算することから、内部スチューデント化残差 (internally Studentized residual) としても知られています。
Studentized Deleted Residual：スチューデント化削除残差、すなわち、外部スチューデント化残差 (externally Studentized residual) は、その残差に関係する当該データポイントを除外したあとに算出した標準誤差を使うスチューデント化残差です。回帰に関する指定した信頼区間の外側にあるスチューデント化 (Studentized) およびスチューデント化削除 (Studentized deleted) 残差はいずれも、外れ値としてフラッグが付けられます。提示される信頼区間は 95% です。スチューデント化削除残差は、スチューデント化残差よりも外れ値に対して遥かに大きな値を算出するので、スチューデント化残差に比べて外れ値の検出の感度が高くなります。

6.16 影響診断

影響診断の結果にはオプションダイアログボックスの Residuals タブで選択した結果の値だけが表示されます。外れ値として評価された全ての結果には、< 記号でフラッグが付けられます。外れ値としてフラッグを付けるトリガーとなる残差の値は、Options ダイアログボックスの Residuals タブで設定します。

Report Cases with Outliers Only (※) を選択していれば、単一または複数の残差に外れ値としてフラッグの付いた観測データだけがレポートされます。その観測データのその他の結果も表示されます。(※ v14 では Report flagged values only)

Row (行)：これは、測定データの行番号です。
Cook’s Distance (クックの距離)：クックの距離 (Cook’s Distance) は、回帰方程式のパラメータ推定において各点が有する影響力の大きさを評価する尺度です。これは、評価する点を分析から除外したとき回帰係数の値がどれだけ変化するかをはかるものです。値が 1 より大きい場合は、その点に影響力がある可能性を示します。クックの距離が 4 より大きい場合、その点は、パラメータ推定値に対して大きな影響があることを示します。ある点のクックの距離が指定した値より大きい場合、影響力があるとしてフラッグが付けられます。提示される値は 4 です。
Leverage (てこ比)：レバレッジ (Leverage：てこ比) の値は、影響力をもつ可能性のある点を識別します。観測データのレバレッジが期待されるレバレッジより大きい場合は、その点に影響力がある可能性があります。提示されるてこ比の値は、期待値の 2.0 倍です。データポイントのてこ比の期待値は次式であらわされます：

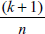
ここで、k は独立変数の数、n はデータポイントの数です。

レバレッジの計算には従属変数しか使用しませんので、独立変数の極値 (大きい値と小さい値) がレバレッジの高い点になる傾向があり、このような点では、独立変数のわずかな変化が従属変数の予測値に大きな影響を与える可能性があります。