20.5 一元配置反復測定分散分析 (ANOVA)

一元配置 (One Way) すなわち１因子の反復測定分散分析を使うのは：

１群の個体が１系列の実験処理や条件によって影響を受けるか否かを調べたいとき。
処理や条件のそれぞれで１因子または１種類の処置しか考慮しないとき。
処理効果が分散の等しい正規分布に従っているとき。

処理効果が正規分布に従っていないことが分かっている場合は、フリードマンの順位に基づく反復測定分散分析 (Friedman Repeated Measures ANOVA on Ranks) を使います。実験処理に因子をもう１つ追加したときの効果を考慮したい場合は、二元配置反復測定分散分析 (Two Way Repeated Measures ANOVA) を使います。処理が１つしかない場合は、対応のある t 検定 (Paired t-test) を実行できます (求める結果に応じて変わります)。

※ Tip：非正規母集団に対して ANOVA を実行しようとした場合、使用する One Way Repeated Measures ANOVA オプションの設定内容によっては、SigmaPlot によりそのデータがパラメトリック検定には適切でないことが報告され、代わりにフリードマンの順位に基づく分散分析を実行するよう提案されます。

一元配置反復測定分散分析について
一元配置反復測定分散分析を実行する
一元配置反復測定分散分析のデータを配置する
一元配置反復測定分散分析オプションを設定する
一元配置反復測定分散分析を実行する
多重比較オプション (One Way RM ANOVA)
一元配置反復測定分散分析の結果を解釈する
一元配置反復測定分散分析のレポートグラフ
1. One Way Repeated Measures ANOVA レポートのグラフを作成する方法

1. 一元配置反復測定分散分析について

一元配置 (One Way) すなわち１因子の反復測定分散分析は、同一群の被験者に対する１系列の実験処置の効果に差があるか否かを各個体の変化を調べることによって検定します。処置の事前と事後に測定した値ではなくその変化を調べることで、各個体応答で生じる差を取り除き、結果として、検定の感度が高く (パワフル) なります。

一元配置反復測定分散分析の計画は、同一群に対して複数の処理が存在することを除けば、対応のある t 検定と基本的に同じです。帰無仮説は、「全ての処理間に差はない」です。

一元配置分散分析は、全ての処理効果は同じ標準偏差 (分散) をもつ正規分布に従うことを前提条件とするパラメトリック検定です。

2. 一元配置反復測定分散分析を実行する

一元配置反復測定分散分析 (One Way Repeated Measures ANOVA) を実行するには：

ワークシートに適切なデータを入力または配置します。詳しくは、一元配置反復測定分散分析のデータを配置するをご覧ください。
必要があれば、One Way Repeated Measures ANOVA オプションを設定します。
Analysis タブの SigmaStat グループにある Tests ドロップダウンリストから以下を選択します：Repeated Measures → One Way Repeated Measures ANOVA
検定を実行します。
レポートグラフを作成します。詳しくは、一元配置反復測定分散分析のレポートグラフをご覧ください。

3. 一元配置反復測定分散分析のデータを配置する

検定するデータのフォーマットには、生データ (raw data) またはインデックス付き (indexed data) データのいずれかを使用することができます。生データの配置では、64 を上限として処理と同じ数だけ列数を使います：それぞれの列に、１つの処理のデータが入ります。生データの各列の長さはいずれも同じである必要があります。

インデックス付きデータの配置にはワークシートの２列を使います。反復測定検定では、統計的要約データを使用することはできません。

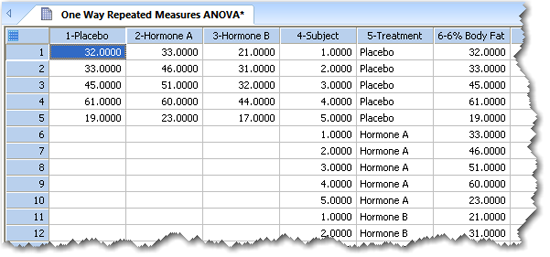
One Way Repeated Measures ANOVA で有効なデータフォーマットの例

上記ワークシートの列１から３には、生データを配置しています。列４、５、６には、インデックス付きデータを配置しており、そのうち、列４は処理のインデックス列、列５は被験者のインデックス列になります。

欠損データポイント

もし欠損値がある場合、SigmaPlot は一般線形モデルを使用して欠損データを自動的に処理します。このアプローチでは、周辺平方和 (marginal sums of squares：一般にタイプ III の平方和、または、調整平方和 (adjusted sums of squares) とも呼ばれます) を使用した仮説検定が構成されます。ただし、列の長さは同じである必要があります。

4. 一元配置反復測定分散分析オプションを設定する

一元配置反復測定分散分析 (One Way Repeated Measures ANOVA) オプションを使用するのは：

データの正規性と等分散性の検定の基準を緩和または厳格にする検定パラメータを調整するとき。
データの統計サマリーテーブルを表示し、残差をワークシートの列に配置するとき。
多重比較を有効にするとき。
検出力 (Power)、すなわち、検定の感度を計算するとき。

一元配置反復測定分散分析オプションを変更するには：

※ Tip：検定オプションを変更したあと検定を実行するにあたり、検定の実行前にデータを選択しておきたい場合は、使用するデータをポインターでドラッグします。

Analysis タブの SigmaStat グループにある Tests ドロップダウンリストから以下を選択します：Repeated Measures → One Way Repeated Measures ANOVA
SigmaStat グループにある Options をクリックします。
Options for One Way RM ANOVA
ダイアログボックスに以下の３つのタブが表示されます：
1. Assumption Checking：データの正規性と等分散性の基準を緩和または厳格にするには、このパラメータを調整します。詳しくは、Options for One Way Repeated Measures ANOVA: Assumption Checking をご覧ください。
2. Results：レポートにデータの統計サマリーを表示したり、ワークシート列に残差を保存するかを指定します。詳しくは、Options for One Way RM ANOVA: Results をご覧ください。
3. Post Hoc Test：検出力 (Power) すなわち検定の感度を計算したり多重比較を有効にします。詳しくは、Options for One Way RM ANOVA: Post Hoc Tests をご覧ください。
検定を継続するには、Run Test をクリックします。
現在の設定内容を適用して、オプションダイアログを閉じるには、OK をクリックします。

4.1 Options for One Way Repeated Measures ANOVA: Assumption Checking

正規性 (Normality) の前提条件の検定では、母集団が正規分布に従っているかをチェックします。等分散 (Equal Variance) の前提条件の検定では、各群の平均値の周りのばらつきをチェックします。

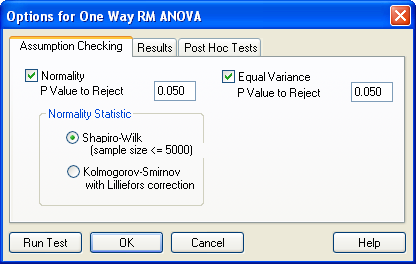
Options for One Way RM ANOVA ダイアログボックスの Assumption Checking オプションの表示例。

Normality の検定：SigmaPlot では、母集団の分布の正規性検定に Shapiro-Wilk または Kolmogorov-Smirnov のいずれかを使用します。
Equal Variance の検定：SigmaPlot では、群平均のばらつきをチェックすることで等分散性を検定します。

正規性および等分散の P 値：P 値により、データが正規分布していないと誤って結論付ける確率が決定されます (P 値は、データが正規分布しているという帰無仮説を誤って棄却してしまうリスクです)。検定によって求められた P 値が、ここで設定した P 値よりも大きければ、検定は採択されます。正規性と等分散のいずれかまたは両方の要件をより厳密なものにするには、この P 値を大きくします。パラメトリックな統計手法では、仮説の棄却が比較的ロバスト (頑健) に検出されることから、SigmaPlot ではこの値を 0.050 としています。P 値をこれよりも大きくすると (例えば、0.100)、そのデータに正規性がないとの判定が出やすくなります。正規性の要件を緩和するには、P 値を小さくします。正規性があるという仮説を棄却するための P 値に小さい値しか要求しないということは、前提とする正規分布からデータが外れていても、それが非正規であると判定される前に、それだけ広く受け入れたいとする意思があることを意味します。例えば、P 値を 0.010 とした場合、あるデータを非正規であると判定するには、0.050 の場合と比べてそれだけ大きく正規性を逸脱していなければなりません。

※ Note：データの分布が極端な状態にあり、これらの手法では検定できない場合があります。たとえば、ルビーンの中央値検定 (Levene Median test) では、分散の大きさが数次の場合は差の検出ができません。このような条件の場合は、前提条件の自動検定に頼らずにデータを視覚的に調べることで容易に見分けることができます。

4.2 Options for One Way RM ANOVA: Results

Summary Table：列または群の観測数 (N)、列または群の欠損値の数 (Missing)、列または群の平均値 (Mean)、列または群の標準偏差 (Std Dev)、および、列または群の平均値の標準誤差 (SEM) を表示します。
Residuals in Column：レポートに残差を表示し、ワークシートの指定列に検定の残差を保存します。列番号を入力するか、ドロップダウンリストから列を選択します。

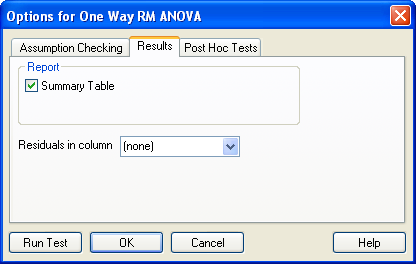
Options for One Way RM ANOVA ダイアログボックスに Summary Table および Residuals オプションを表示した例。

4.3 Options for One Way RM ANOVA: Post Hoc Tests

Power：検出力 (Power) すなわち検定の感度は、もし群間に真の差がある場合、その差を検定によって検出できる確率です。
Use Alpha Value：アルファ (α) は、誤って差があると判断しても良しとする確率です。SigmaPlot で提示される値は、α = 0.05 です。この設定は、誤りを許容する確率が 20分の１であることを示します。すなわち、P < 0.05 であれば有意な差があると判断できることになります。α 値を小さくすると、有意差があると結論付ける要件がそれだけ厳格なものになりますが、差があるにもかかわらずないと結論付けてしまう可能性はそれだけ大きくなります。α 値を大きくすると、差があると結論付ける要件はそれだけ容易になりますが、誤判定をレポートしてしまうリスクが増加することになります。

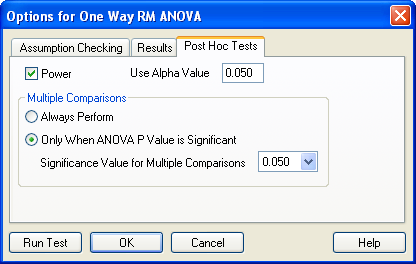
Options for One Way RM ANOVA ダイアログボックスに Power および Multiple Comparison オプションを表示した例。

Multiple Comparison (多重比較)：一元配置反復測定分散分析 (One Way Repeated Measures ANOVA) では、幾つかの処理群の間に差がないという仮説を検定しますが、どの群に差があるのか、すなわち、群間の差の大きさは分かりません。これらの差を特定するのが多重比較プロシージャです。ANOVA で差を検出するか否かの判定に使用する P 値は、Options ダイアログボックスの Report タブで設定します。一元配置反復測定分散分析 (One-Way RM ANOVA) で求められた P 値が、このボックスで指定した P 値よりも小さければ、群間に差が検出されたことになるので、多重比較が実行されます。
- Always Perform：ANOVA で差が検出されたか否かにかかわらず常に多重比較を実行します。
- Only When ANOVA P Value is Significant：ANOVA で差が検出されたときだけ多重比較を実行します。
- Significance Value for Multiple Comparisons：Significance Value for Multiple Comparisons ドロップダウンリストから .05 または .01 を選択します。この値は、多重比較で処理間に有意差があると誤って結論付ける見込みを決定します。値が .05 であれば、多重比較で誤って差を検出する可能性が 5% 以下であれば多重比較で差が検出されることになります。値が .10 であれば、多重比較で誤って差を検出する可能性が 10% 以下であれば多重比較で差が検出されることになります。
※ Note：多重比較が開始されると、Multiple Comparison Options ダイアログボックスが表示され、多重比較の手法を選ぶよう指示されます。

5. 一元配置反復測定分散分析を実行する

検定を実行する前にお持ちのデータを選択しておきたい場合は、対象となるデータをマウスポインタでドラッグしておきます。

Analysis タブの SigmaStat グループにある Tests ドロップダウンリストから次を選択します：Repeated Measures → One Way Repeated Measures ANOVA検定ウィザードの One Way RM ANOVA — Data Format パネルが表示され、データフォーマットを指定するよう指示されます。

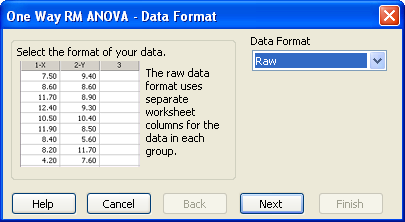
検定ウィザードの One Way RM ANOVA — Data Format パネル。データフォーマットを選択するよう指示されます。
Data Format ドロップダウンリストから適切なデータフォーマットを選択します。詳しくは、反復測定検定のデータフォーマットをご覧ください。
Next をクリックして、検定に使用するデータ列を選択します。検定を選択する前に列を選択していれば、その列が
Selected Columns に表示されます。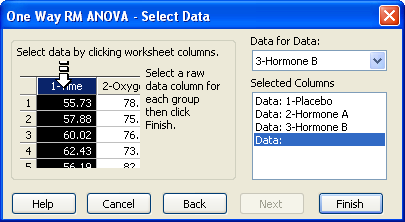

検定ウィザードの One Way RM ANOVA — Select Data パネル。データ列を選択するよう指示されます。
Selected Columns リストに別のワークシート列を割り当てたい場合には、ワークシートで直接その列を選択するか、Data for Data ドロップダウンリストからその列を選択します。Selected Columns リストの一行目に割り当てられるのは最初に選択した列で、以後同様に列を選択するごとにリストの２行目以降に割り当てられてゆきます。各行には、選択した列の番号またはタイトルが表示されます。ワークシートの３列を最低限選択するよう指示されます。
選択した内容を変更するには、リストの割り当てを選択したあと、ワークシートから列を選択しなおします。Selected Columns リストの内容をダブルクリックすることによって、列の割り当てを消去することもできます。
Finish をクリックすると、選択した列に対して One Way RM ANOVA が実行されます。正規性と等分散性の検定を実行するよう指定しており、いずれの検定にも合格しなかった (failed) 場合、SigmaPlot は、警告を表示し、ノンパラメトリックのフリードマンの順位に基づく反復測定分散分析 (Friedman Repeated Measures ANOVA on Ranks) を使用して分析を継続するよう提案します。詳しくは、フリードマンの順位に基づく反復測定分散分析をご覧ください。P 値が有意なときだけ多重比較を実行するよう選択しており、P 値が有意でない場合、この検定の完了後に One Way RM ANOVA レポートが表示されます。詳しくは、一元配置反復測定分散分析の結果を解釈するをご覧ください。多重比較の P 値が有意な場合、または、多住比較を常に実行するよう選択している場合は、Multiple Comparisons Options ダイアログボックスが表示され、多重比較の手法を選択するよう指示されます。詳しくは、多重比較オプション (One Way RM ANOVA) をご覧ください。

6. 多重比較オプション (One Way RM ANOVA)

一元配置反復測定分散分析 (One Way Repeated Measures ANOVA) では、幾つかの処理群の間に差がないという仮説を検定しますが、どの群に差があるのか、すなわち、群間の差の大きさは分かりません。実験群間の比較を行うことによってこれらの差を特定するのが多重比較プロシージャです。

P 値が有意なときだけ多重比較を実行するよう選択しており、ANOVA によって算出された P 値が基準となる P 値と等しいか小さかった場合、または、Options for One Way RM ANOVA ダイアログボックスで常に多重比較を実行するよう選択している場合は、Multiple Comparison Options ダイアログボックスが表示され多重比較の検定法を指定するよう指示されます。ダイアログボックスの左上には、ANOVA によって算出された P 値が表示されます。詳しくは、一元配置反復測定分散分析の結果を解釈するをご覧ください。

一元配置反復測定分散分析 (One Way Repeated Measures ANOVA) で選択できる多重比較検定は、以下の７種類があります：

Holm-Sidak 検定：詳しくは、Holm-Sidak 検定をご覧ください。
Tukey 検定：詳しくは、Tukey 検定をご覧ください。
Student-Newman-Keuls 検定：詳しくは、Student-Newman-Keuls (SNK) 検定をご覧ください。
Bonferroni の t 検定：詳しくは、Bonferroni の t 検定をご覧ください。
Fisher の LSD 検定：詳しくは、Fisher の LSD (Least Significance Difference) 検定をご覧ください。
Dunnett の検定：詳しくは、Dunnett の検定をご覧ください。
Duncan の多重範囲検定：詳しくは、Duncan の多重範囲をご覧ください。

一元配置反復測定分散分析 (One Way Repeated Measures ANOVA) で選択できる多重比較には２つのタイプがあります。選択できる比較タイプは、選択した多重比較検定法によって変わります。

All pairwise 比較は、処理対の全ての可能な組み合わせを比較します。
Versus Control (対照群との多重比較) は、全ての実験処理を単一の対照群と比較します。

7. 一元配置反復測定分散分析の結果を解釈する

一元配置反復測定分散分析 (One Way Repeated Measures ANOVA) のレポートには、処理の変動要因 (source of the variation) をあらわす分散分析表が生成されます。この表に表示される内容は、自由度 (DF: degrees of freedom)、平方和 (SS: sum of squares)、データテーブルの各要素の平均平方 (MS: mean squares)、および、F 統計量とそれに対応する P 値です。表示されるその他の結果は Options for One Way RM ANOVA ダイアログボックスにあります。

多重比較の表を生成することも可能です。多重比較の結果についても Options for One Way RM ANOVA ダイアログボックスで指定します。多重比較の実行に使用する検定法は、Multiple Comparison Options で指定したものです。

One Way RM ANOVA の結果の導出に関する詳しい説明については、統計学の参考書をご覧ください。

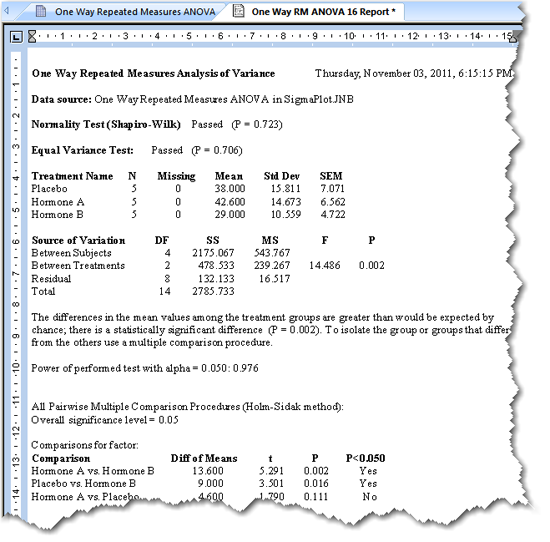
結果の説明

数値による結果に加えて、拡張された結果の説明が表示されることがあります。この説明テキストは、Options ダイアログボックスで有効または無効にすることができます。表示される小数点以下の桁数についても Options ダイアログボックスで指定できます。

7.1 欠損データセルがある場合

お持ちのデータに空白セルではない欠損値が含まれている場合、一般線形モデルを使用して算出された結果であることがレポートに表示されます。分散分析表には、F の算出に使用した自由度、推定した平均平方の式の一覧が表示され、サマリーテーブルには、推定した最小二乗平均が表示されます。

One Way RM ANOVA の結果の導出に関する詳しい説明については、統計学の参考書をご覧ください。

7.2 Normality Test

正規性の検定：正規性の検定 (Normality test) の結果には、変化の差が正規母集団から抽出されたデータであるという前提条件の検定にお持ちのデータが合格したか (passed) 不合格したか (failed) 、および、この検定で算出された P 値が表示されます。全てのパラメトリック検定では、元になる母集団が正規分布に従っていることが要求されます。

この結果は、Options for One Way RM ANOVA ダイアログボックスで正規性の検定を無効にしない限り表示されます。

7.3 Equal Variance Test

等分散性の検定：等分散性の検定 (Equal Variance test) の結果には、変化の差が同じ分散を持つ母集団から抽出されているという前提条件の検定にお持ちのデータが合格したか (passed) 不合格したか (failed) 、および、この検定で算出された P 値が表示されます。元になる母集団の分散が等しいことは、全てのパラメトリック検定の前提条件となります。

この結果は、Options for One Way RM ANOVA ダイアログボックスで正規性の検定を無効にしない限り表示されます。

7.4 Summary Table

Options for One Way RM ANOVA ダイアログボックスでこのオプションを有効にしていれば、SigmaPlot によってサンプルサイズ N、欠損値、平均値、標準偏差、平均値の差、および、標準偏差、標準誤差を一覧とするサマリーテーブルが生成されます。

N (Size)：該当する列または群の観測値の数です。
Missing：該当する列または群の欠損値の数です。
Mean：列の平均値です。観測値が正規分布に従う場合、平均値は分布の中心になります。
標準偏差 (Std Dev)：ばらつきの尺度です。観測値が正規分布に従う場合、平均値の上下１標準偏差分の間に約３分の２が収まり、平均値の上下２標準偏差分の間に観測値の約 95% が収まります。
平均値の標準誤差 (SEM)：標本を元に算出した平均値から真の母平均を近似するときの目安となる尺度です。

7.5 Power

実行した検定の検出力 (Power) は、Options for One Way RM ANOVA ダイアログボックスでこのオプションを無効にしない限り表示されます。

One Way Repeated Measures ANOVA の検出力 (Power)、すなわち感度は、処理間に真の差がある場合、その検定で処理間の差を検出できる確率です。検出力が 1 に近づくほど、その検定の感度は高くなります。

反復測定分散分析の検出力は、サンプルサイズ、比較する処理の数、差があると誤って報告する可能性 (アルファ)、測定された群平均の差、および、測定された標本の標準偏差によって影響を受けます。

アルファ：アルファ (α) は、誤って差があると結論付けることを許容する確率です。この誤りを、第一種の誤り (Type I error) と呼ぶこともあります (第一種の誤りは、効果がないという帰無仮説が真であるにもかかわらずそれを棄却するときです)。この値は、Options for One Way RM ANOVA ダイアログボックスで設定します。提示される α = 0.05 という値は、許容する誤りを 20分の１にすることを示します。α の値を小さくするほど、有意差があるとの結論に至る要件はそれだけ厳格になりますが、その反面、差があるにもかかわらず差がないと結論付けてしまう可能性は高くなります (第二種の誤り：Type II error)。α の値を大きくすれば、差があるという結論付けは容易になりますが、その反面、偽陽性 (false positive) をレポートするリスクが高まります。

7.6 ANOVA Table

分散分析表：分散分析表には、One Way Repeated Measures ANOVA の結果が一覧で表示されます。

DF (Degrees of Freedom: 自由度)：自由度 (Degrees of freedom) は、分散分析の感度 (検出力) に影響を及ぼす群数とサンプルサイズをあらわします。

被験者間 (Betwen Subjects) の自由度は、被験者数の尺度です。
被験者内 (within subjects) の自由度は、処理数を調整した測定総数の尺度です。
処理 (Treatments) の自由度は、処理数の尺度です。
残差 (Residual) の自由度は、被験者と処理の数を調整した測定数間の差の尺度です。
全体 (Total) の自由度は、被験者数と処理数の両方の尺度です。

SS (Sum of Squares：平方和)：平方和は、分散分析表の要素それぞれに関連するばらつきの尺度です。

被験者間の平方和は、各被験者の平均応答のばらつきの尺度です。
被験者内の平方和は、各被験者に存在する全体のばらつきの尺度です。
処理の平方和は、被験者間の平均処理応答のばらつきの尺度です。
残差の平方和は、被験者間の差を考慮した後の全ての測定データ間に存在するばらつきの尺度です。
全体の平方和は、全体のばらつきの尺度です。

MS (Mean Squares：平均平方)：平均平方には、母分散に関する２つの推定量が表示されます。

処理の平均平方は、次式であらわされます：

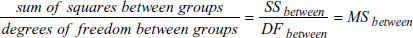
残差の平均平方は、次式であらわされます：

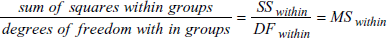
7.7 F Statistic

F 統計量：F 検定統計量は、効果の差の尺度として使用する比です。欠損値がない場合、F 統計量は次式で算出されます：

F 比が 1 の周辺にあれば、処理間に差はない (そのデータは処理効果はないという帰無仮説から成っている) と結論付けることができます。

もし、F の値が大きい場合、各効果の平均値の分散は、処理のランダムな変動から期待される分散より大きいので、その処理効果に差がある (処理間の差は統計的に有意である) と結論付けることができます。

P Value：P 値は、群間に真の差があると誤って結論付けてしまう確率です (例えば、F 値に基づいて帰無仮説を誤って棄却する、すなわち、第１種の誤り (Type I error) を犯してしまう確率です) 。P 値が小さいほど、異なる母集団から標本が抽出されている確率は大きくなります。伝統的には、P < 0.05 であれば、有意差があると結論付けることができます。

7.8 Expected Mean Squares

Expected Mean Squares (期待される平均平方)：もし欠損データがある場合、一般線形モデルを使用してそのモデルで期待される平均平方が算出され、その線形方程式が表示されます。これらの方程式は、一般線形モデルが使用されたときだけ表示されます。

7.9 Multiple Comparisons

多重比較：多重比較を実行するよう選択していれば、群どうしを対比較した表が表示されます。詳しくは、多重比較オプション (One Way RM ANOVA) をご覧ください。多重比較プロシージャは、Options for One Way RM ANOVA ダイアログボックスで有効にします。多重比較プロシージャーで使用する検定法は、Multiple Comparison Options ダイアログボックスで指定します。

ANOVA の結果からは、２つ以上の群に差があるかどうかまでしか分からないため、具体的にどの処理に差があるかを決定するには、多重比較の結果を使用します。多重比較の結果の特定のタイプは、使用する比較検定法、および、比較の仕方、すなわち、全ての組み合わせ (pairwise) か、対照群との比較 (versus a control) かによって異なります。

全ての対の組み合わせ (All pairwise comparison) の結果には、組み合わせ可能な全ての群の対の一覧が表示されます。全ての対の組み合わせには、Holm Sidak, Tukey, Student-Newman-Keuls, Fisher LSD, Duncan’s test および Bonferroni t-test があります。
単一の対照群との比較では、選択した対照群 (control group) との比較しか表示されません。対照群は実際に行う多重比較プロシージャで指定します。対照群との比較検定には、Bonferroni t-test, the Dunnett’s, Fishers LSD, および Duncan’s tests があります。

パラメトリックな多重比較プロシージャの結果の導出に関する詳しい説明は、統計学の参考書をご覧ください。

Holm-Sidak Test の結果：Holm-Sidak 検定は、All pairwise 比較と Versus Control (対照群との比較) の両方で使用します。Tukey や Bonferroni 検定よりもパワフルであるため、それらでは検出できない差を検出することができます。一対比較 (pairwise comparison) 検定における第一のプロシージャーとして推奨されています。この検定を実行すると、計算された全ての比較の P 値が小さい順に並び替えられます。そして、それぞれの P 値は、臨界水準 (critical level) と比較されます。この臨界水準は、検定の有意水準 (検定オプションで設定) 、P 値の順位、および、比較の総数に応じて変化します。ある P 値が臨界水準を下回っていれば、該当する２群間に有意差があることをあらわします。
Bonferroni t-test の結果：Bonferroni t-test には、各群の対の平均値の差が一覧で表示され、各対の t 値が計算され、その比較について P < 0.05 であるか否かが表示されます。Bonferroni t-test は、全ての群の比較にも、対照群との比較にも利用できます。t 値が大きいものであれば、比較した２群の差は統計的に有意であると結論付けることができます。比較した P 値が 0.05 より小さい場合は、誤って有意差があると結論付けてしまう可能性は 5% よりも小さくなります。この値が 0.05 より大きければ、確信を持って差があると結論付けることはできません。この平均値の差が２群の間の差の大きさの尺度となります。
Tukey, Student-Newman-Keuls, Fisher LSD, Duncan’s, および Dunnett’s Test の結果：Tukey, Student-Newman-Keuls (SNK), Fisher LSD, および Duncan’s tests は、いずれも群の全ての対の組み合わせを比較するものです。これに対して、Tukey Fisher LSD, and Duncan’s は、対照群とそれ以外の群との比較に使用するものですので、このタイプの比較では推奨されません。対照群とその他の全ての群とを比較できるのは Dunnett’s test のみです。いずれの検定も、q 検定統計量を計算し、その対比較で P < 0.05 または < 0.01 であるか否かを表示します。q 値が大きいものであれば、比較した２群の間の差は統計的に有意であると結論付けることができます。比較した P 値が 0.05 より小さい場合は、誤って有意差があると結論付けてしまう可能性は 5% よりも小さくなります。この値が 0.05 より大きければ、確信を持って有意差があると結論付けることはできません。Difference of the Means (平均値の差) が２群の間の差の大きさの尺度となります。
p は、q の算出に使用するパラメータです。p が大きければ、有意差を示すのにそれだけ大きな q が要求されます。p は、比較する群平均の順位に関する差の指標です。SNK 検定では群平均に大きいものから小さい順にそれぞれ順位を付けるので、比較における平均値の数の隔たりが p になります。例えば、比較する平均値が４つある場合、最大と最小を比較すると p=4 となり、二番目に小さなものと最小のものを比較すると p=2 になります。

ある群が他の群と比べて有意差がないことが分かった場合、差のない２群の順位 p の間にある順位 p を持つ全ての群についても、有意差がないとみなされますので、これらの比較については DNT (Do Not Test) という結果が表示されます。

8. 一元配置反復測定分散分析のレポートグラフ

One Way RM ANOVA の結果を使用して以下を含む最大３つのグラフを作成できます：

事前と事後の折れ線グラフ (Before and after line graph)：一元配置反復測定分散分析では、複数の折れ線を使って処理後の各被験者の変化をプロットします。詳しくは、事前と事後の折れ線グラフ (Before and After Line Plots) をご覧ください。
残差のヒストグラム (Histogram of the residuals)：一元配置反復測定分散分析のヒストグラムには、指定した範囲の生の残差が定義した間隔セットを使用してプロットされます。詳しくは、残差のヒストグラム (Histogram of Residuals) をご覧ください。
残差の正規確率プロット (Normal probability plot of the residuals)：一元配置反復測定分散分析の確率プロットには、生の残差の度数がプロットされます。詳しくは、正規確率プロット (Normal Probability Plot) をご覧ください。
多重比較グラフ (Multiple comparison graphs)：一元配置反復測定分散分析の多重比較グラフでは、ある重要な因子の水準間の有意差がプロットされます。詳しくは、多重比較グラフ (Multiple Comparison Graphs) をご覧ください。

8.1 One Way Repeated Measures ANOVA レポートのグラフを作成する方法

One Way Repeated Measures ANOVA test レポートを選択します。
Report タブの Results Graphs グループにある Create Result Graph をクリックします。
Create Result Graph ダイアログボックスが表示され、その中に One Way Repeated Measure ANOVA の結果で利用できるグラフのタイプが表示されます。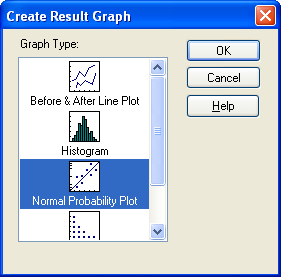

レポートのCreate Result Graph ダイアログボックス
Graph Type リストの中から作成したいグラフタイプを選択して OK をクリックするか、リスト内のグラフをダブルクリックします。選択したグラフがグラフウィンドウに表示されます。