28.2 カーブフィット機能について

カーブフィット機能は、方程式のパラメータ (係数) を変化させることによって、実験データに最も近似するような方程式のパラメータを求めるものです。方程式と初期パラメータの値は必ず必要となります。SigmaPlot に組み込まれている方程式にはいずれも、曲線の方程式と初期パラメータがあらかじめ設定されています。

カーブフィット機能では、方程式のパラメータを最大 25 まで、独立変数を最大 10 まで使用することができます。また、カーブフィットでパラメータ値を求める際にその探索範囲を制限するためにパラメータの制約条件を最大 25 まで指定することができます。

回帰曲線のあてはめ機能では、重み付き最小二乗法 (weighted least squares) を使用して精度を向上させることも可能です。

28.2.1 カーブフィッティングのアルゴリズム

SigmaPlot のカーブフィット機能では、独立変数の係数 (パラメータ) の探索に方程式と実験データのあてはめを最適にする Marquardt-Levenberg アルゴリズムを使用します。

このアルゴリズムでは、従属変数の実測値と予測値の間の平方和の差を最小にするパラメータの値を求めます。

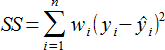
ここで、 y_i は従属変数の実測値、 ŷ _i は予測値をあらわします。

このプロセスは、反復計算 (iterative) です。すなわち、カーブフィット機能では、方程式のあてはまり具合を調べるのに、まず初期推定値をパラメータに代入します。そして、残差平方和 (residual sum of squares) がこれ以上有意に減少しなくなる最適な推定値が見つかるまで計算を繰り返します。最適な推定値が見つかった状態を収束 (convergence) と言います。詳しくは、Marquardt-Levenberg アルゴリズムの参考文献をご覧ください。

28.2.2 Marquardt-Levenberg アルゴリズムの参考文献

• Press, W. H., Flannery, B. P., Teukolsky, S. A., and Vetterling, W. T. (1986). Numerical Recipes. Cambridge: Cambridge University Press.
• Marquardt, D.W. (1963). An Algorithm for Least Squares Estimation of Parameters. Journal of the Society of Industrial and Applied Mathematics, 11, 431-441.
• Nash, J.C. (1979). Compact Numerical Methods for Computers: Linear Algebra and Function Minimization. New York: John Wiley & Sons, Inc.
• Shrager, R.I. (1970). Regression with Linear Constraints: An Extension of the Magnified Diagonal Method. Journal of the Association for Computing Machinery, 17, 446-452.
• Shrager, R.I. (1972). Quadratic Programming for N. Communications of the ACM, 15, 41-45.