Geometry Expressions が行う計算について
1. 条件 / 作図
Geometry Expressions を効果的に活用するには、このソフトウェアの幾何学モデルがどのような仕組みで動作するかを理解することが役に立ちます。
通常の対話型幾何学ソフトウェアは、作図ベースのモデルです。ユーザーは、入力する幾何データを指定し、作図セットを指定することで、出力されるデータを定義することになります。
一方、シンボル型の幾何学モデルにおいては、条件ベースのアプローチによって、その定義をより簡単に進めることができます。ユーザーは、図形を描画し、それに数式による条件を与えることによってモデルを指定することになります。
以下に例を示します。AB には長さが a になるような条件を与えます。BC には長さが b になるような条件を与えます。AB には、BC に対して直角になるような条件を与えます。BD には、AC に対して直角になるような条件を与えます。そして、D には AC 上を通るような条件を与えます。
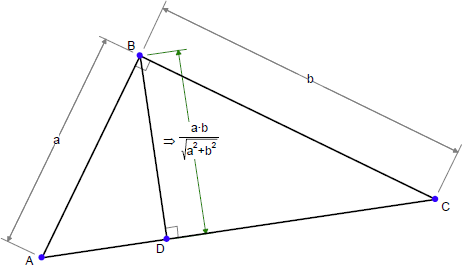
こうした条件が入力されると、Geometry Expressions の内部に図形を作図するためのシーケンスが作成されます。
左図の作図シーケンスの内容は、以下のようになります:
- 任意の位置に点 A を配置する。
- 点 A から距離 a だけ離れた任意の方向に点 B を配置する。
- AB に対して垂直で B を通る直線を作成する。
- B から距離 b だけ離れたこの直線上に点 C を配置する。
- AC に対して垂直で B を通る直線を求める。
- この直線と AC との交点に D を配置する。
作図シーケンスが定められると、Geometry Expressions によって、この内容を元に数式に基づく図形モデルが作成されます。また、この定義の中で使用されている変数については、いずれも、指定された条件を満たす図形を作成するために、標本数値も使用されることになります。
ここから次のような疑問が出てきます:
ステップ1と2で任意の位置と任意の方向を配置すると、どのようなことが起こるのでしょうか?
Geometry Expressions によって変数が作成され、その変数が A の座標に設定されます。デフォルトで使用される座標は (u0,v0) に設定されています。次に、別の新たな変数が作成され、その変数が直線 AB の傾きとして使用されます。デフォルトで使用されるこの変数は θ0 に設定されています。
ステップ4で、B から距離 b だけ離れた点は直線上に2つありますが、このうちどちらを使用するかはどのような基準で決定されるのでしょうか?
直線 AB の左側の点を使用するか、直線 AB の右側の点を使用するかは、描画された内容で判断されます。
a と b の標本値は、何を元に取られているのでしょうか?
この事例は簡単です。描画された内容を元に AB の距離を単純に測定し、その値を a の標本値として使用しています。描画された内容を元に BC の距離を測定し、それを b の標本値として使用しています。これとは別に、1つの変数が複数の箇所で使用されていたり、複雑な数式が絡んでいるような事例では、適切な標本値を求める数値計算が Geometry Expressions によって実行されます。しかし、こうして求められた値であっても、ユーザーは変数パネルを使用していつでもその値を設定しなおすことが可能です。
Geometry Expressions が作図シーケンスを作成できない場合はどうなりますか?
以下のダイアログボックスが表示されます:
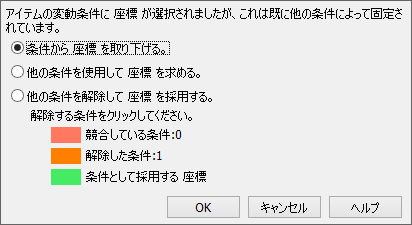
他の条件を取り下げるか、新たに追加しようとしている条件をキャンセルできます。
Geometry Expressions では作図シーケンスが読み進められますので、このダイアログの出現でたびたび不愉快な思いをさせられるようであれば、条件を指定する際に作図シーケンスのことを思い描くことで、その原因を説明するのに役立てることができるでしょう。
2. 幾何学的両義性の判断
幾何学の授業を受けると、2つの辺とそれらに挟まれた1つの角によって、1つの三角形が一意的に定まることを学びます。2辺とそれに挟まれていない角では、そうはいきません。もし、ユーザーが2辺とそれに挟まれない角を使って三角形を定義する場合、シンボリック型の幾何学プログラムに期待されることはどのようなことでしょうか?それは、毅然として原則を守り、解の求めを断固拒否することもあるでしょう。さもなくば、冗長になりますが両方の解を提示することもあるでしょう。あるいは、ユーザーの求めに応じて内容を判断し、それにふさわしい解を提示することもあるでしょう。
Geometry Expressions で採用されているのは、描画された内容をその指針とする後者のアプローチです。例えば、以下の図では、2つの三角形 ABC と ADC には、いずれも長さが a と b の辺と、2つの辺には挟まれていない角 θ があります。2つの三角形は、描画内容において ADC は鈍角であるのに対して、ABC は鋭角である点で異なります。Geometry Expressions では、この角度の鋭さと鈍さを使用して問題とされている三角形が区別されます。
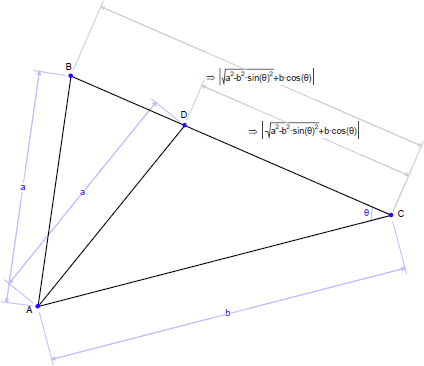
2つ目の例として、次の条件を与えたタコを描画する場合、2つの解が考えられます。1つは凸型の形状、もうひとつは凹型の形状です。Geometry Expressions では、この場合も、描画された内容に基づいて問題とされる図形が判断されます。
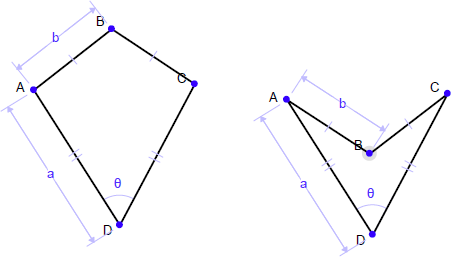
3. システムが追加する条件
Geometry Expressions では、作成したモデルにすべての条件を与える必要はありません。ユーザーが考慮しなかった条件のパラメータについては、幾何エンジンによって補完されます。
例えば、以下に示す図形は、固定的変換条件のモジュロが与えられているに過ぎません(多くの図形問題で多く見られるもの)。
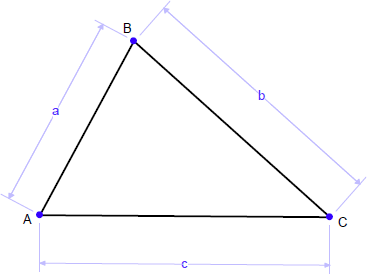
従って、任意の点の座標を求める場合、それらは、システムが加えた変数を使って求められることになります。
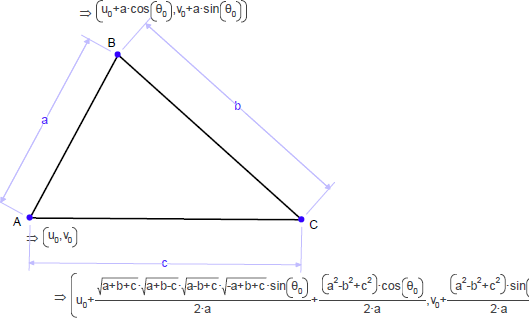
システムが加えた変数は、点 A の位置と、線分 AB の方向であることが分かります。
4. 軌跡とアニメーション
Geometry Expressions では、任意の変数について軌跡、および、包絡線を作図したり、図形のアニメーションを定義することができます。例えば、以下に示す図形では、変数 t の値のとりうる範囲について軌跡を作図することができます(それ以外の変数は一定とします)。
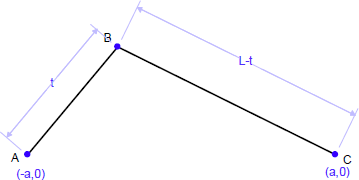
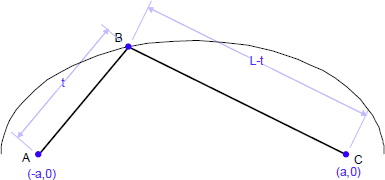
インタラクティブな数値計算型幾何システムをお使いの方であれば、線分や曲線上の点の動作をベースとするこのアニメーションの考え方をご存知でしょう。このタイプのアニメーションは、Geometry Expressions の曲線上に点を配置する条件とパラメータベースのアニメーションを合わせることで、簡単にモデル化することができます。
曲線上に配置される点の割合 t は、以下に示すように、曲線の種類に応じて様々な定義法があります:
- 線分 AB の場合は、点 (1-t) A + tB で定義されます。
- 円の場合は、円の中心の角度 t を定める円周上の点で定義されます。
- 軌跡または包絡線の場合、パラメータ値 t における点で定義されます。
例えば、以下の図形では、点 D は、AB 間の割合 t で定義され、点 E は、BC 間の割合 t で定義されています。曲線は、F が 0 から 1 まで動いたときの軌跡です。
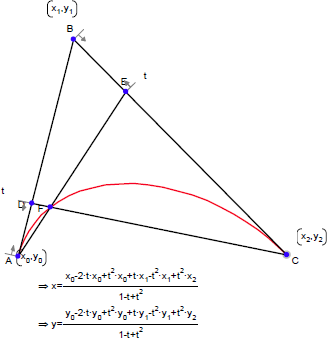
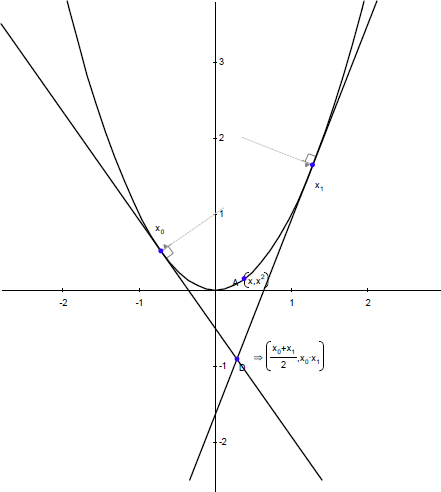
以下の例に示す曲線は、点 (x,x2) の軌跡です。2つの接線は、パラメータ値に x0 と x1 をとるこの曲線上の点において作成されたものです。
5. 変数の固定とドラッグ
初期設定では、Geometry Expressions モデルで点をドラッグすると、モデルの各種パラメータで使用されている標本数値が、ドラッグに合わせて、できる限り最適になるよう調整されます。
例えば、4つの棒をつなげた以下のモデルでは、点 B をドラッグすると、ab の長さと角 θ が適切に調整されることになります。
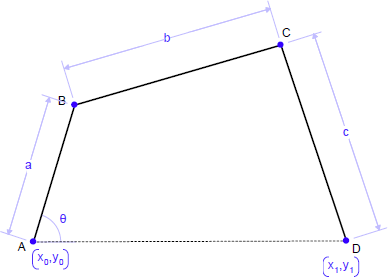
しかし、AB と BC の部分はドラッグしても固定されたかのように振る舞うようにし、角 θ のみを動かしたい場合があるとしましょう。パラメータを固定することで、これを実行することができます:
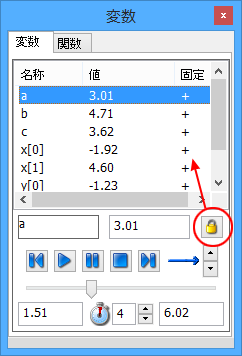
例えば、a の値は、変数パネル上ではこれまでどおり設定変更できますが、モデルをドラッグしても動かなくなります。
