分割法における多元配置実験

はじめに
実験の計画
結果の分析

1.はじめに

実験の計画によっては、無作為化を制限しなければならないことがあります。そうしなければ、実験を行うのが現実的に困難になる場合があるからです。例えば、多くの実地試験において温度を変化させるのは容易ではありません。この問題を解決する手段のひとつに、農業試験の分野にその起源を発する分割法があります。これは “whole-plot” と呼ばれる農場の広大な領域を、実験者が分割して処理できるよう “subplot” と呼ばれる幾つかの小さな区画に分割するものです。例えば、何品種かの作物を植え付ける場合、各品種それぞれを whole-plot に植え付け、その subplot それぞれには異なる種類の肥料を与えます。

分割区法の分析は、統計の専門家でさえ扱いにくいものです。しかし、Design-Expert® version 12 を使用すれば簡単に分析することができます。

Design-Expert ではどのように分割法を計画し分析するのか、Montgomery による『Design and Analysis of Experiments』の例を追ってみていきましょう。必要に応じて、囲み内のセクションは飛ばしてください。これらは、さらに時間をかけて詳しく学びたい人向けの補足的内容となっています。

※このケーススタディの詳細について
実験の構造および、この特別な事例の詳細については上記で参照した文献の第 8 版のセクション 14.4 (Willey 刊, 2012)の “The Split-Plot Design” を参照してください。

事例の背景

ある製造業者が、紙の引っ張り強度（tensile strength）に関して、３種類のパルプ調整法と４水準の蒸解温度（加熱温度）の効果を調査したいと考えています。これら 12 種類の組み合わせすべてを実行するには丸１日かかります。

統計的検出力を高めるために、製造業者は12回の一般的な要因配置計画を３日間繰り返し、合計 36 回の試行実験を行うことにしました。しかし、この実験はランダムに実行できそうにありません。そのかわり、３日間のそれぞれの日に実験者は一回分のパルプを調製し、それを4つのサンプルに分けて４種類の温度で蒸解（加熱分解処理）することにしました。この処理は、他の2つの方法で調製されたパルプについても繰り返されます。

この実験のフローチャートは以下の通りです。

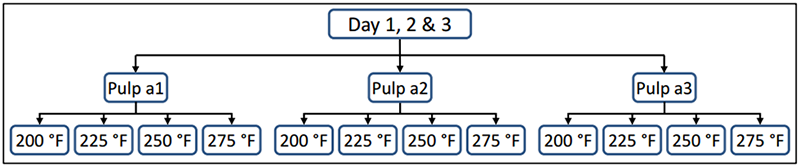
分割法は、統計学的に次のように構成することができます。

Whole-plot: ３種類のパルプ調整法（変更困難な因子）
Subplot: ４種類の温度で蒸解される４種類のサンプル（変更容易な因子）

この計画を、分割法でブロック化 (日で分割) した一般的な要因計画として設定することにします。

2.実験の計画

それでは、計画を構築していきましょう。この計画は、ブロックに日数を使った通常の一部実施要因配置計画として実行します。Design-Expert の起動画面から、New Design ボタンをクリックしてください (または、ツールバーの空白シートアイコンか、“File” -> “New Design” をクリックしても同じです) 。

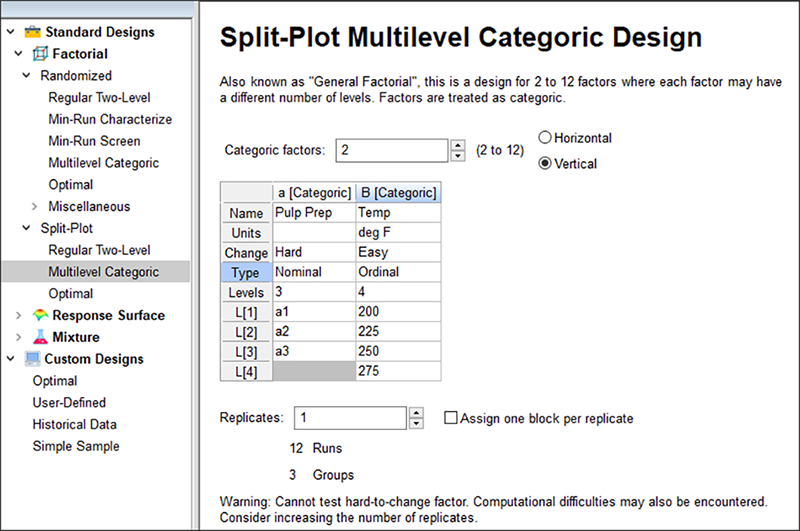
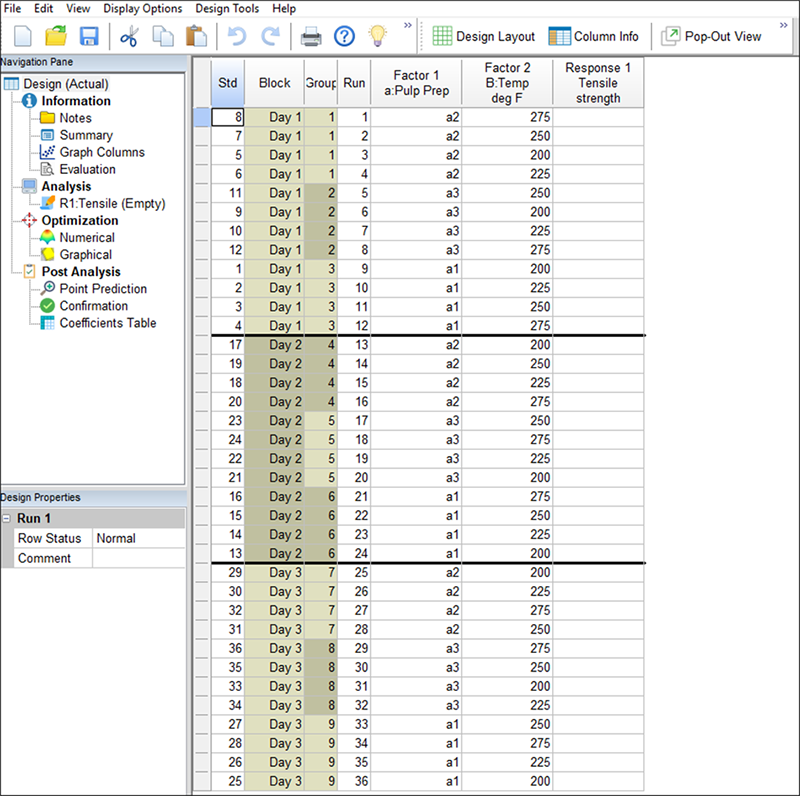
次に Split-Plot でデフォルトの Factorial タブから、“Multilevel Categoric” をクリックします。因子数は “2” を選択してください。“Vertical” ラジオボタンをクリックします。それから Factor A の名称に「Pulp Prep」と入力します。これは既に変更困難な因子（HTC）として設定されているため、そのままにしておいてください。マウスを Levels 列まで下に移動して「3」と入力します。次に、処理名 L(1)、L(2)、L(3) に、「a1」、「a2」、「a3」と入力します。

さらに同じ画面で、2番目の因子の名称を「Temp」とし、その単位を「deg F」、水準数を「4」、処理名をそれぞれ「200」、「225」、「250」、「275」とします。この因子は既にプログラムによって、変更容易な因子として設定されています。Type には “Ordinal” を選択して、これが数値タイプであることを指定します。以下の画面と同じようになるはずです。

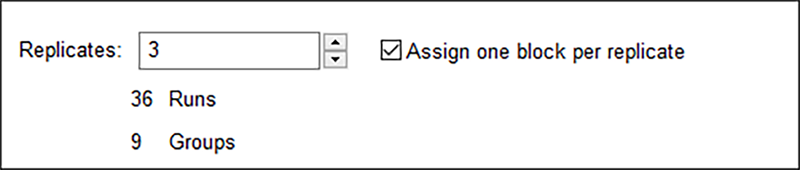
この際HTCの検出力が欠けているため、注意してください。これを修正するには、Replicates に「3」を入力し、Assign one block per replicate（１反復あたり１ブロックを割り当て）をチェックして（√）36 回の試行を 9 グループについて作成します（36 = 4水準×３因子×3回反復）。

“Continue” をクリックします。次に、Block Names に「Day 1」、「Day 2」、「Day 3」を入力します。

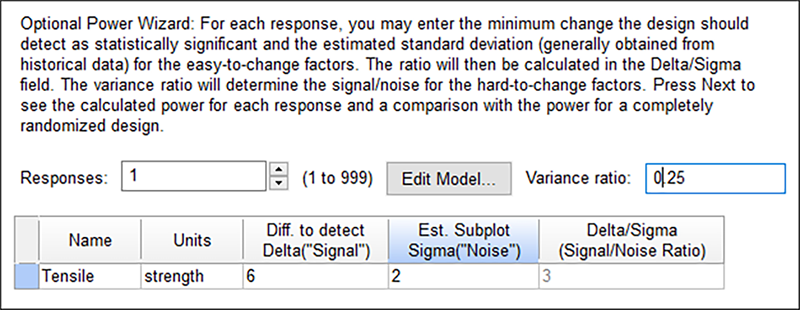
もう一度 “Next” をクリックし、Name に「Tensile」、Units に「strength」と入力します。次に、計画の検出力を評価するために Delta に「6」、Sigma に「2」と入力します。また、Variance ratio を「0.25」に変更します。

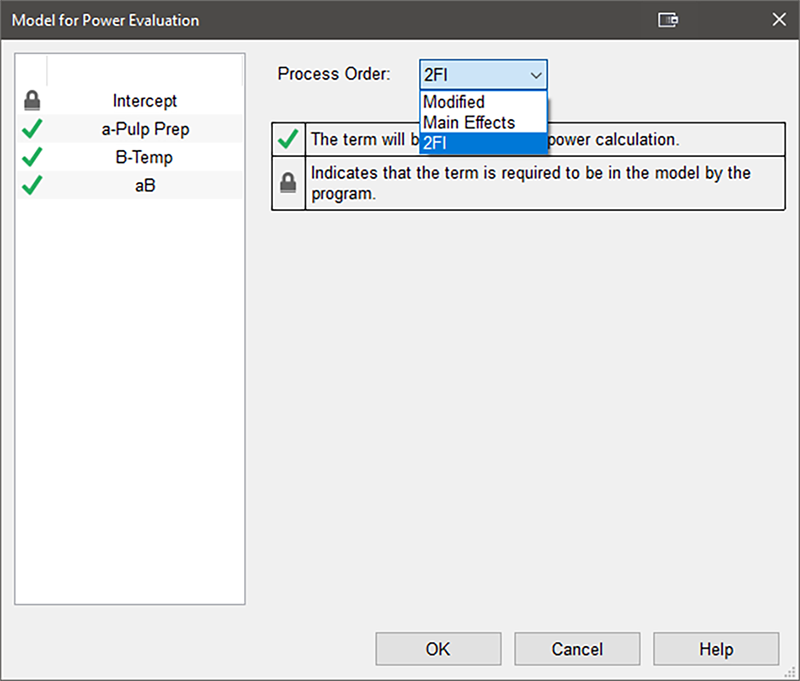
“Edit Model…” をクリックし、以下のように Order のモデルを “2FI” に変更したら、“OK” をクリックします。

※ 分散比の背景について
Design-Expert では、グループ（whole-plot）のための残差分散は、分散比 1 がデフォルトとなります。しかし、この事例の場合、whole-plot 因子は変更困難であるにも関わらず、subplot の温度と比べて少ない変動で制御できます。

P.S. 順序を変更する場合は、実験者が pulp prep の交互作用に興味を持っていなければなりません。そうでない場合は順序を変更する必要はありません。実験者達がこのモデル項（aB）が”妥当”な検出力の水準（一般的に 80% が許容範囲）で推定できるか知りたいのはこうした理由によります。

“Next” をクリックして計画の検出力を見直します。分割法における無作為化の制限によって変更困難な因子 “a”（Pulp prep）の視覚効果の検出力は減少したのに対して、変更容易な因子 “B”（Temperature）の視覚効果の検出力と、その交互作用 “aB” は、わずかですが増加したことに注意してください。

※ 分割法によるグループ化の影響について
この計画の構造のため、変更困難な因子（whole-plot）と変更容易な因子（subplot）との相互作用を、subplotの誤差に対して検出する必要があります。

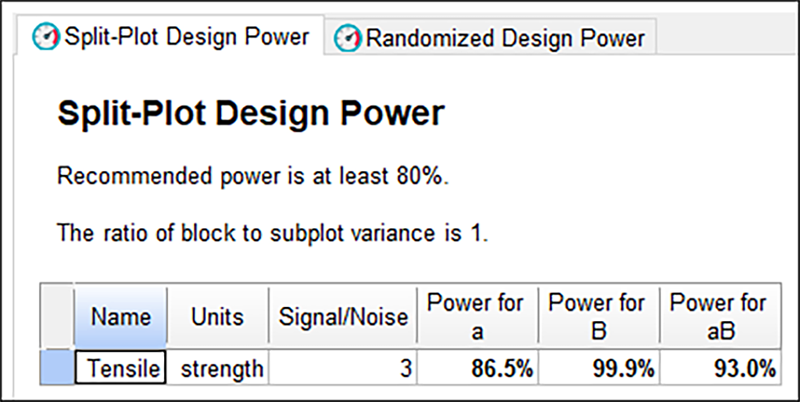
変更困難な因子 “a”（Pulp Prep）の検出力が減少していますが、推奨される最小値（80%）を依然として上まわっている点に注目してください。“Finish” をクリックして、計画設計ウィザードを終了します。警告ダイアログでは “OK” を押して、グループ間の因子をリセットします。変更困難な因子 “a”（Pulp Prep）の水準によるグループで計画が表示され、このうち変更容易な因子 “B”（Temperature）は完全にランダムな順序で表示されます。

分割法用に設計された計画（実行順序は無作為化されるため、画面はおそらくこの画像とは異なります）

通常はこの段階で、実際の実験で使う試行シートとしてこれを印刷し、実験で得られた伸縮強度の応答結果を記録します。

3.結果の分析

“Help” -> “Tutorial Data” -> “Paper Pulp” をクリックして、計画を読み込んでください。

分割法の解析は、完全に無作為化された実験とは別に行われなければなりません。各統計的検定を正確に行うため、Design-Expert では以下に対して個別に２つの ANOVA が適用されます

Whole-plot の処理（pulp prep）
Subplot の処理（temperature）及びwhole plot と subplot における個別の交互作用

それから、有益な診断とモデルグラフを得るためにすべてのモデルに当てはめます。

メインウインドウの左側のツリー構造にある “R1:Tensile” とラベル付けされたAnalysisノードをクリックするところから始めましょう。今度は、progressive ツールバーに表示された “Mode” タブを指定します。2因子交互作用（2FI）の条件があらかじめ選択され、これらは緑色のでラベル付けされます。任意の項が無事に取得できるかどうかを確認するために、“Auto Select…” ボタンをクリックしてプログラムを有効にします。それから、以下の画像のように Criterion を “p-values” に、Selection を “Backward” に変更します。

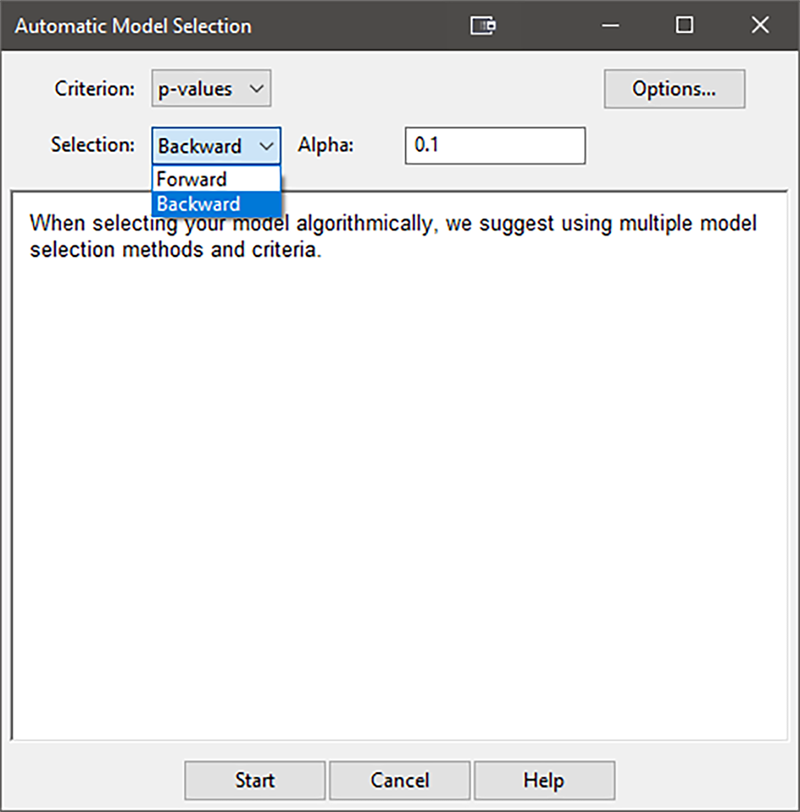
“Start” ボタンをクリックすると、モデルから削除されている “Alpha out” 基準（デフォルトでは p 値が 0.1）を超える任意の条件と共にアルゴリズムの選択が列挙されます。これらは、“Accept” をクリックすると Error（）に再指定されます。ANOVA の統計に目を通した後で、条件を削除したい場合は元に戻ってそれをダブルクリック（または、右クリックして任意のメニューを選択）するだけで削除できます。

※ 分割法における多元配置実験による効果の選択に関する注意
この計画は構造上の理由から、２水準における因子のみの実験のようにグラフィカルで扱いやすい、効果の半正規プロットは作成されません。その代わり、Auto Select… アルゴリズムの一つが起動します（この事例では backward を使用しました）。詳細については、Help ボタンをクリックしてください。

“ANOVA（REML）” タブに進み、p 値が有意かどうか確認をします。この場合、計画されたすべてのモデル項が除去プロセスで存在し続けています。つまり、これらすべては統計的に有意となります。

※ 用語についての注意
ご存知でしょうが、ANOVA は analysis of variance の頭文字をとったもので、すべての DOE のモデルの有意性を評価するための基本的手法です。試行は完全に無作為化することができます。しかし、分割法では成分の分散は REML と呼ばれる別の手法（制限付き最尤法）によって推定されます。計画の構造によって REML は、通常の最小二乗推定法の ANOVA とぴったり一致することもありますが、ほとんどの場合、結果は若干異なります。

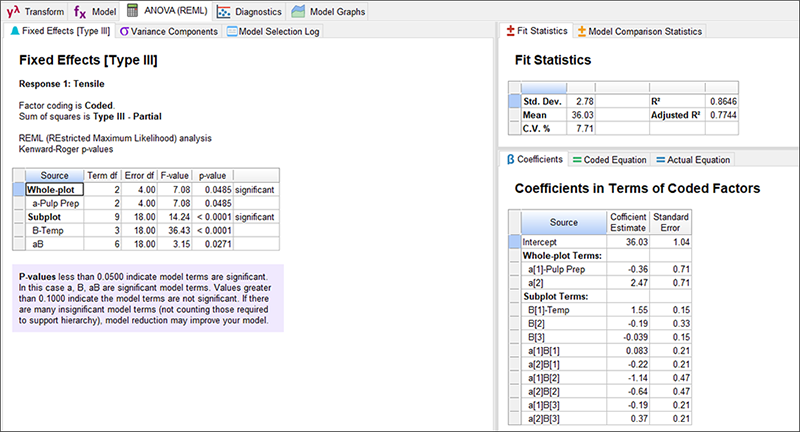
※ ANOVA（REML）レポートに表示された統計の詳細: チュートリアルで説明するのは概要のみです。Help による検索、コンテンツの詳細（参考文献を含む）など、この画面に表示されたすべてを参照してご自身でさらに知識を深めていってください。

“Diagnostics” タブをクリックして、統計の次の段階（統計的推定の検証）に進みましょう。まずは残差の正規プロットです－これは外部スチューデント化を使用するとあらゆる相違を最も効果的に示すことができます。この場合、明らかな異常はありません－ポイントは通常のデータから推定されたラインに集まっています。

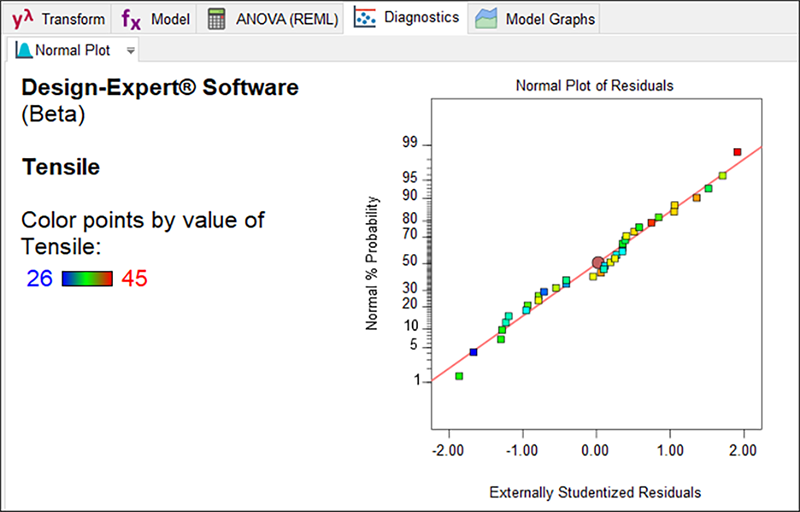
Diagnostics ツールを使用して使用可能なすべてのグラフを検討します。異常は何も見当たらないはずです。

“Model Graphs” に進んでください。Factors Tool の B: Temperature バーを右クリックし “X1 axis” に変更します。

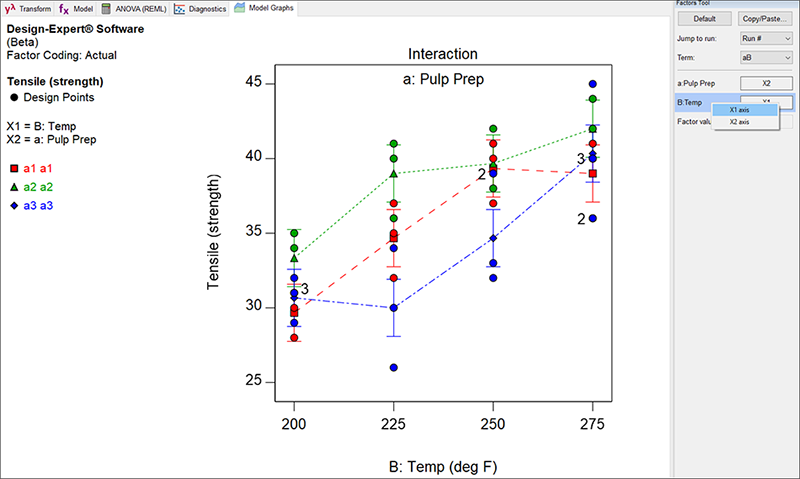
3水準それぞれのパルプ調整における、連続的因子温度の交互作用プロットが表示されます。このグラフからパルプ調整 a2（緑色の三角形の記号）が、最大の引っ張り強度になると分かります。このa2が温度変化に対して最も安定するであろうことは明らかです（特にカ氏 225 から 275 の領域）。

結論

これは、変更困難なパルプ調整の処理に分割法による実験を計画した独創的な手法です。Design-Expert を使用すれば、無作為化の制限によって、どのように検出力が減少するかについて有益な洞察を得ることができます。この事例では、パルプ調整（因子 “a”）の実効果は、重要とされる最小値をはるかに超えており実験は成功しています。