RSM における最適な計画構築
1.はじめに
このチュートリアルでは、例外的な条件が含まれる不規則なプロセス空間に Design-Expert® ソフトウェアで応答曲面法(RSM)実験を組み立てる方法を紹介します。急いで学習したい方で、コンピュータを利用した最適化計画の知識は最低限でよい場合は、囲み内のセクションを飛ばしてください。しかし、これらのセクションは読み進めていく上で、時間をかける価値が十分にあります。
ある料理研究家が、小麦製品の調理に関して様々な時間と温度の中から最適な組み合わせを見いだしたいと考えています。一連のスクリーニングと、綿密な要因計画の結果、最適なプロセス条件の究明に必要な2つの因子の範囲を以下のように絞り込みました:
- A. Temperature (温度) : 110 ~ 180℃
- B. Time (時間): 17 ~ 23 分
ところで、でんぷんを望ましくゲル化させるには、110℃の温度で加熱する場合(実験領域の一番低い側)、少なくとも19分は必要であることが既に分かっています。一方、加熱する温度を180℃に上げた場合、でんぷんがゲルになるまでにかかる時間はわずか17分で済みます。
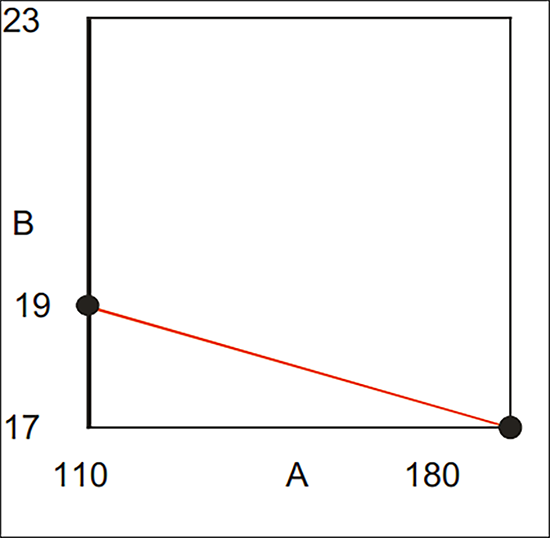
以上を要約すると、因子 A の水準が最も低い場合、因子 B は 19 より大きい値である必要がある一方、因子 B の水準が最も低い場合、因子 A は 180 より大きい値である必要があるということです。問題が複雑に絡み合ってきたので、この実験の応答曲面は、もしかしたら、波打っている可能性があると想像します。つまり、応答曲面法(RSM)で使用される標準的な2次モデルでは、正確な予測は期待できないだろうと考えたわけです。その結果、この計画に望ましいモデルとして 3次モデルを推奨します。
このような問題は、Design-Expert® の制約条件ツールと最適計画機能を使ってうまく対処することができます。
2.実験の計画
Design-Expert を起動したらツールバーの左側にある空白シートアイコン ![]() をクリックして計画の作成を開始します。
をクリックして計画の作成を開始します。
“Standard Designs” の下にある “Response Surface” をクリックして、メニューを展開します。計画の種類として “Optimal(custom)” を選択します。それから以下のように、 L[1](下限値)と L[2](上限値)に値を入力します。
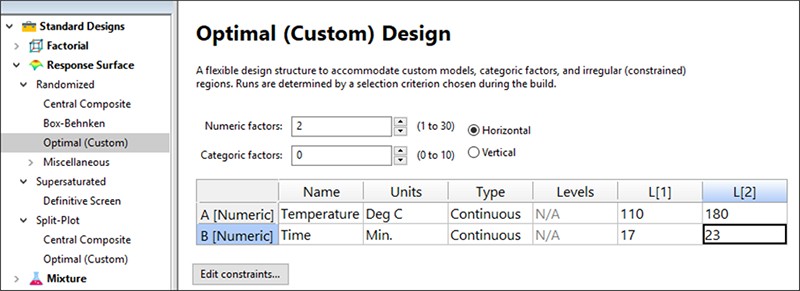
3.多重線形制約条件の作成
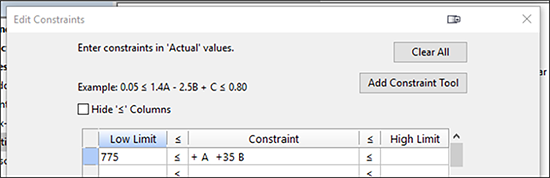
テーブルの下にある “Edit Constraints” ボタンを押してください。
この段階で、計画の多重線形制約条件が分かっていれば、若干の数学的変形を行って、それらを直接フィールドに入力できます。
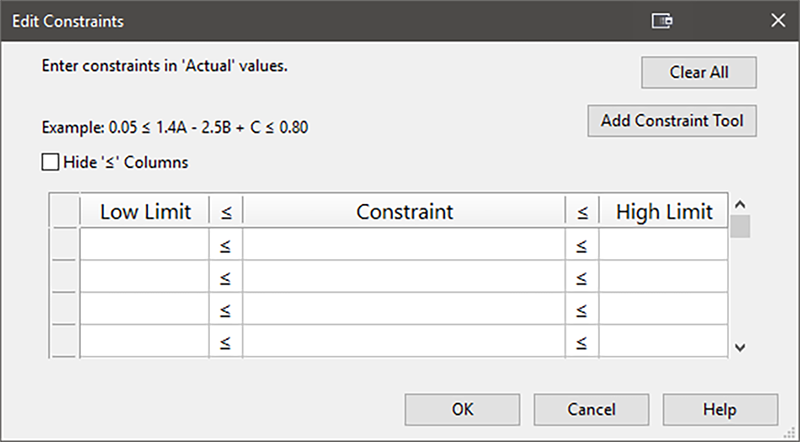
| ※ 注意 上に示した多因子の制約条件は、方程式として次の形式で入力する必要があります。 ここで、βL と βU は、それぞれ、下限値と上限値をあらわします。制約条件の方程式を展開するためのガイドラインについては、Anderson と Whitcomb による著書 RSM Simplified の Appendix 7A をご覧ください。この事例の因子 A、B のように、両方の因子が制約点 (CP) を超えるようにしたい場合、この方程式は実験領域の境界を表すものとなります。 ここで、LL は低水準をあらわします。この事例の場合、低水準の値は、因子 A では 110、因子 B では 17 となります。両因子の CP は、因子 A では 180、因子 B では 19 となります (制約線の両端点をグラフで表すと以下のようになります) 。 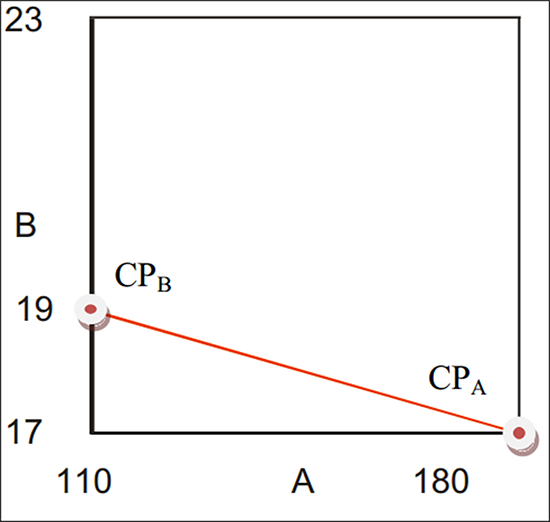 二つの制約点 以上の値を代入すると式は以下ようになります ところで、ソフトウェアでこれを使用するには、1次式に直す必要があります。これは以下に示すように、簡単な演算を使って変形することができます。 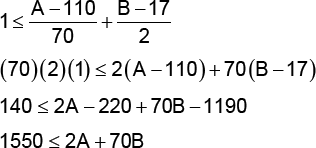 両辺を2で割ると、この方程式は 775 ≤ A + 35B と変形できます。このような方程式を最終的に得ることができれば、制約条件の式として直接入力できるようになります。なお、これと同じ式は、RSM 計画の設定を行う際、制約点の内容を元に Design-Expert でも求められます。 |
制約条件ツールの使用例
条件式をフィールドに直接入力するのではなく、Design-Expert に計算させることにしましょう。“Add Constraint Tool” ボタンをクリックしてください。計画の制約条件として既に入力されている内容をもとに、適切なデフォルト値があらかじめセットアップされています。
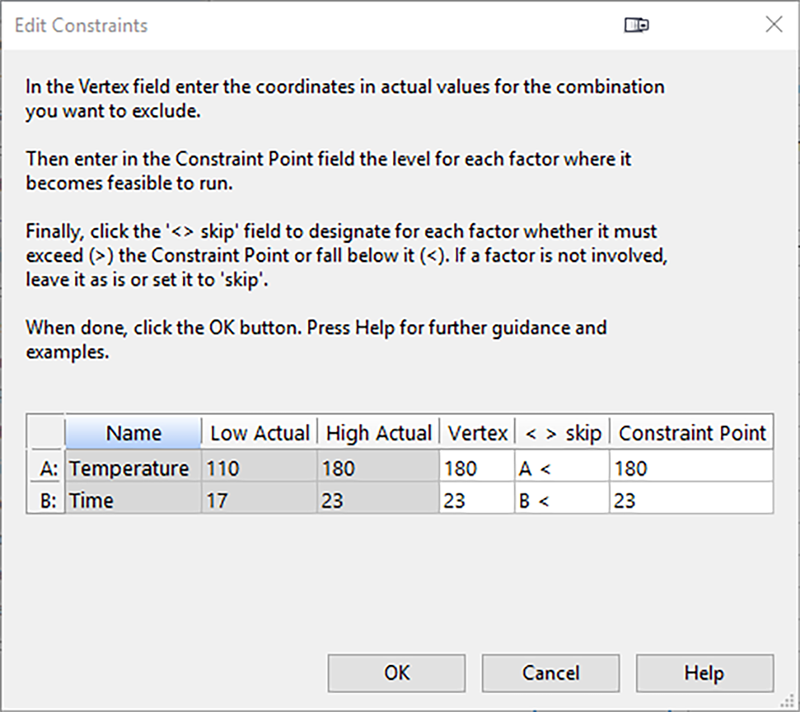
画面上の説明で指示されているとおり、まず始めに除外すべき値の組み合わせ、すなわち、幾何学的に言えば Vertex を指定します(以下の図において、赤で表示されている部分に該当します)。
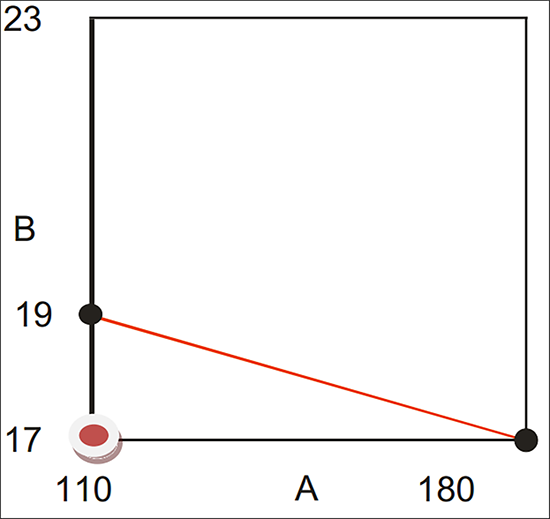
A の Vertex ドロップダウンリストをクリックして、“110” に変更します。
続いて、B の Vertex 座標を “17” に変更します。
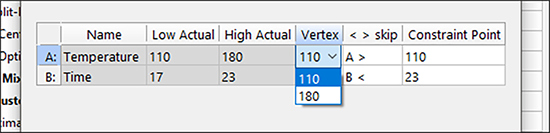

画面の説明にもあるように、次のステップは、Constraint Point フィールドの入力です。温度が低水準の値 110 をとるとき、目的を達成できる B(time)の水準を入力します。入力する値は「19」です。これは、でんぷんがゲル化にかかる最小時間に相当します。

不等号が Design-Expert によって正しい向き(>)に変更された点に注目しましょう。
続いて、因子 A(Temperature)とその Constraint Point に関心の矛先を戻しましょう。B(Time)がその低水準である頂点をとるとき、A(温度)は「180」より大きい必要があります。

不等号は Design-Expert によって前もって正しい向き (>) 変更されている点に注目しましょう。
“OK” をクリックして、Design-Expert で計算された多重線形制約条件の方程式が、数学的に得られた内容と同じであることをご確認ください。
制約条件の不等式の内容がこれで正しいかを確認したら “OK” をクリックして、“Next” をクリックしてください
4.最適計画の構築
Search オプションと Optimality の判定基準は、それぞれデフォルトで指定されている “Best” と “I” のままで結構です。
| ※ 注意 デフォルトで指定された内容の、是非に関する画面上の有益な情報を確認してください。このような応答曲面計画では、推奨される最適化の基準として I-optimality が選択されていることに注意してください。最適モデル選択画面については、スクリーンチップス(電球アイコン)をクリックしてください。Design-Expert が Coordinate Exchange と Point Exchange から、どのように “Best” な検索を実行するかについて記述された説明を読むことができます。 |
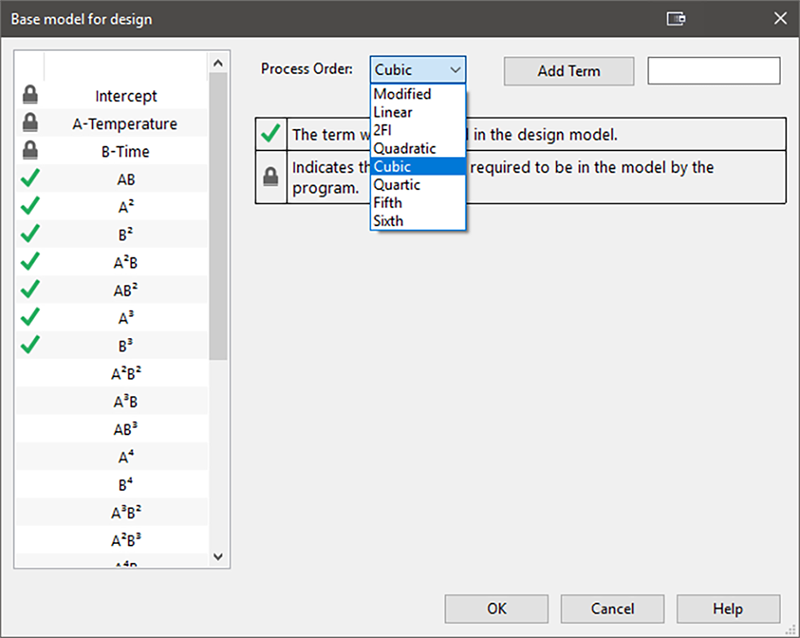
“Edit Model” ボタンを押して、デフォルトの2次モデルを3次モデルに引き上げます(実験者はこの応答が波型になるだろうと考えたことを思い出してください。デフォルトで指定された2次モデルでは、波型の曲面に適合する期待ができないからです)。
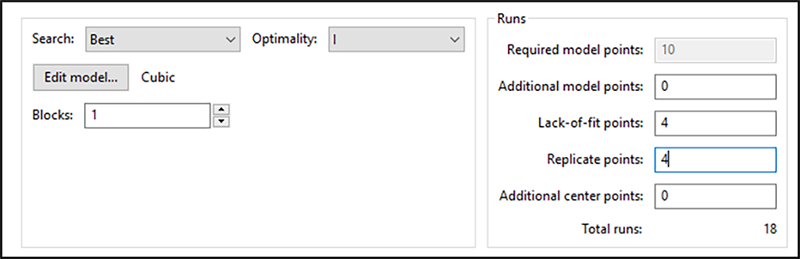
デフォルトで指定された試行内容は、実験者が希望する試行設定のうち lack of fit(不適合度)と replicates(反復回数)の値が少し高めです。試行回数を制限するために、Lack of fit points の値をデフォルトで指定された 5 から「4」に変更し、また、Replicates(反復回数)についても「4」に減らすことにしましょう。実験者は、これによって計画の堅牢性が低下することを重々承知していますが、実験の試行には相当のコストが掛るため、ここではあえて、試行数を減らす道を選んだ訳です。
“Next” をクリックして応答入力に移ります。応答入力は、デフォルトで指定された一般的な “R1” のままで結構です(この実験の最終結果はここでは確認しません)。続いて、“Finish” をクリックして、制約条件付きプロセス空間の最適計画を構築します。
| ※ 注意 Design-Expert では、この段階で “bootstrap”(ブートストラップ)と呼ばれる計画点の集合が無作為に選ばれます。この集合は、モデル選択画面で設定した仕様に合致するまで、繰り返し別の点と交換されることになります。 |
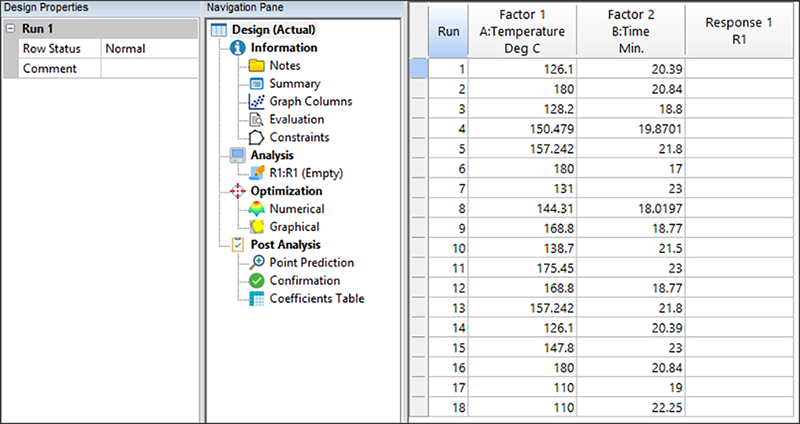
ブートストラップの無作為化により、出来上がる計画はその都度異なるものとなりますが、基本的にはいずれも(あらゆる実用的な用途として)最適なものとなります。続いて、選択された点の内容を確認してみましょう
- “Select” ボタン(左上のセル)を右クリックして、“Design ID” を選択します
- Id 列のヘッダを右クリックして、“Sort Ascending” を実行します
- “Select” ボタンを右クリックして、“Space Point Type” をクリックします
現在テーブルには、計画点を識別する形状タイプが表示され、ID でソートされた状態で計画点の一覧が表示されているはずです。ブートストラップの無作為化により、実際の点は以下に示すものと異なる場合があります。
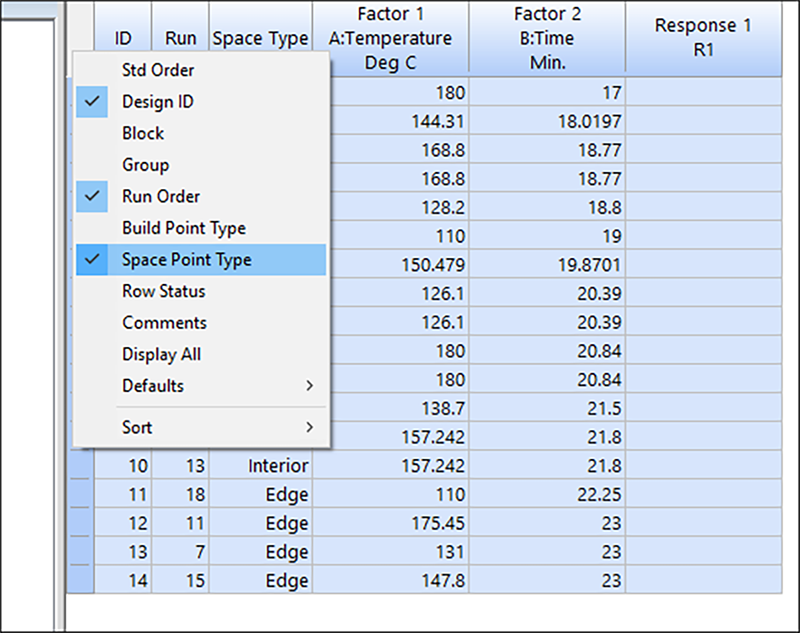
| ※ 注意 計画の内容をざっと見渡してください。その中で “Vertex” とラベルの付いた点タイプを見てみましょう。(A, B)の値の組み合わせのうち(110, 17)は除外されていますか?そうなっているはずです(この組み合わせだとでんぷんがゲル状になるには、温度が低すぎて、時間が短すぎます)。 P.S. Design-Expert がこの計画をどのように構築したかを確認するには、Design ブランチ下の “Summary” ノードをクリックしてください。 |
これらの因子の組み合わせが3次モデルの適合に充分な情報となり得るかを正確に評価してみましょう。Design の “Evaluation” ノードをクリックしてください。
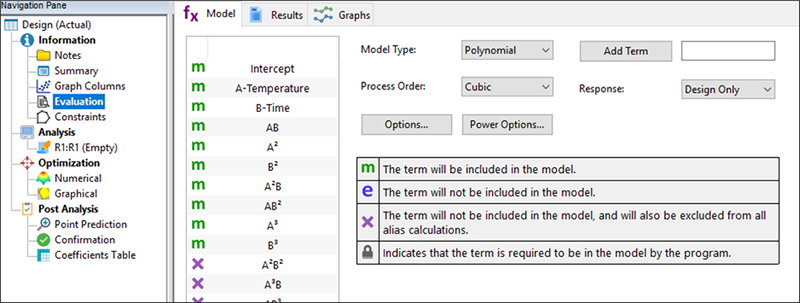
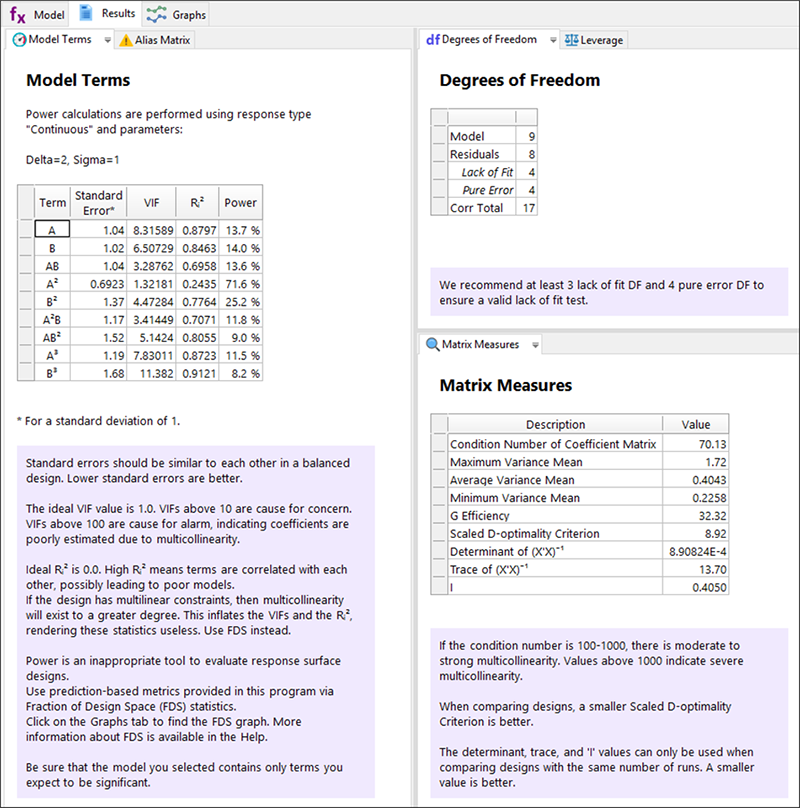
指定された計画内容に基づいて、評価する次数に3次がプログラムにより自動的に選択されています。“Results” をクリックして、実験がどの程度うまく計画されたかを確認してみましょう。
エイリアスは特に見つかりませんでした:出だしとしては上々です。しかし、検出力統計の値の低さと、各項の統計値にばらつきがあることに驚く人がいるかもしれません。これは、多重線形制約条件の計画では良く起こることです。従って、代わりに FDS(設計空間率)グラフを使用して、このような実験の適正な規模を評価することをお勧めします。これについては、このすぐ後にとりあげます。
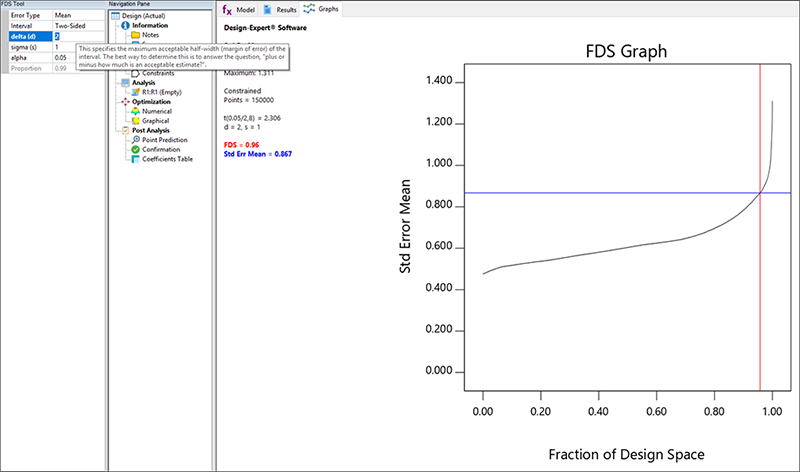
それでは、“Graphs” ボタンをクリックしてみましょう。ここで、応答の標準偏差の大きさが2であれば、実験者が期待する差異であると仮定しましょう。別の言葉で言い換えると、S/N 比が 2 であるということです。左側の FDS Tool にある d に 2 と入力します(“d” は応答の差異 response difference を意味します)。Tab キーをクリックして、標準偏差(“s”)を 1 として、この予測精度の水準を達成する設計空間の割合を見てみましょう。
FFDSの値はグラフの左側に凡例として示されていますが、この場合、理想的な値は 0.8 以上となります。この計画に問題はありません。
| ※ 注意 FDS に関する豊富な情報は、スクリーンチップスを使ってワンタッチで表示させることができます。実際にこれを開き、“FDS Graph Tool” と書かれたリンクをクリックしてみてください。 |
Graphs Toolbar にある “Contour” をクリックして、等高線上で計画点がどこに配置されるかをご確認ください(実際に表示されるものとは若干異なる場合があります)。
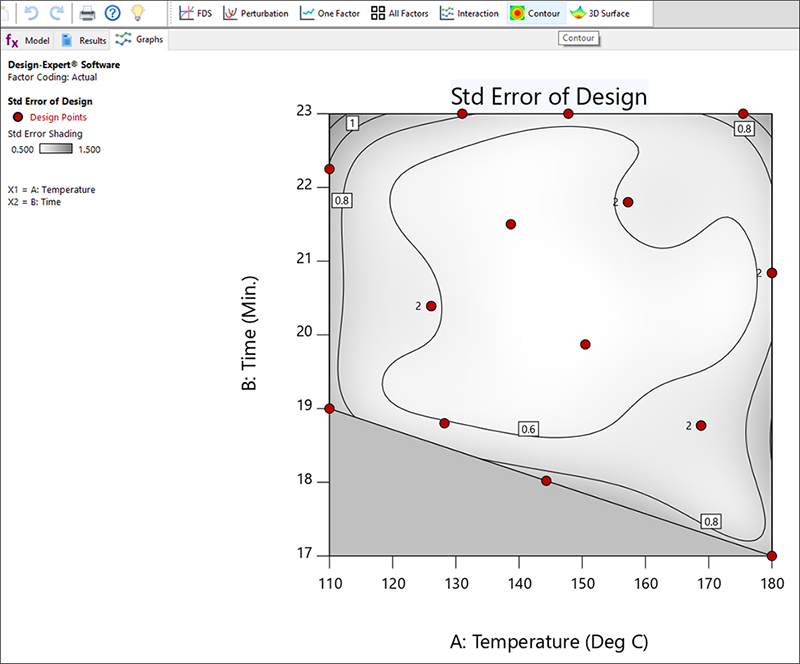
計画点どうしの間隔は好ましい距離で保たれ、また、反復試行の選択についても道理に適ったものであると考えられます(“2” とラベルのついた四隅の点)。“View” -> “3D Surface” を選択し(または Graphs Toolbar から 3D Surface を選び)、標準誤差の曲面を表示させてみましょう。
この計画の場合、標準偏差プロットにおいて比較的平坦な曲面が作成されます。つまり設計空間全体を通して非常に均一な予測精度が得られることになります。
応答曲面法による最適化計画のチュートリアルは、これで終了です。
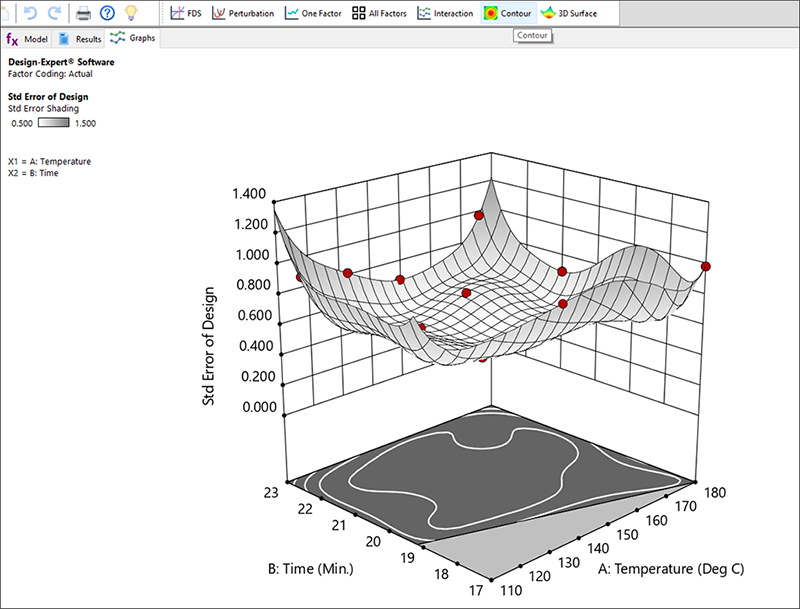
| ※ 注意 この後、何をするかはあなた次第です。Design-Expert が選択する実際の計画点によっては、最大の頂点、辺沿いの点、あるいはその他の地点に、更に数回の試行を追加したくなるかもしれません* 。計画に変更を加えたら、前に戻ってそれを評価します。標準誤差の 3D グラフを表示させ、追加した計画点の位置がどれだけ低くなったかを確認していきます。いずれのケースにおいても、Design-Expert の最適化機能には、ユーザーが指定したモデルの適合に必要な多岐にわたるプロセス条件が用意されており、ユーザーが候補として指定した可能性のある領域で処理を実行できるので、安心して作業を進めることができます。 * 計画割付表を変更する方法については、一元配置実験(Part2:上級編) で詳しく紹介されています。 |
