「宇宙の相転移を紐解く手助けとして」

PDFダウンロード

直感的に使えて非常に多くの良質な関数が含まれているのが魅力です。
日々の計算ノートとして役に立っています。

業務 と ご研究の内容について、お教えください

初期の宇宙はビッグバンと言われる超高温高密度状態から宇宙膨張によって徐々に低温低密度の現在の宇宙へと冷えていったと考えられています。

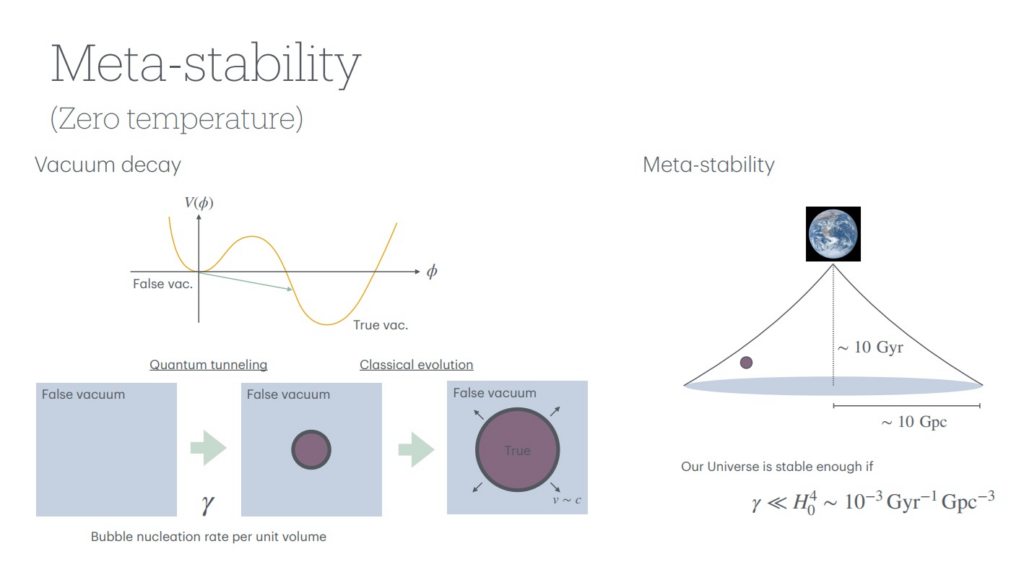
この時、水蒸気が水、氷へと温度によって相転移するように、高温粒子で満たされた宇宙も温度によってその性質が変化します。特に水の例のように状態が滑らかに変化しない相転移は、宇宙の進化に特異な影響を与え得るということが議論されています。

私の研究内容の一つは、過去に起きた可能性のある相転移や遠い未来に起こる可能性のある相転移について理論的に解析し予言を行う研究です。

Wolfram 製品をどのような場面で使用されていますか？

日常的に使用している場面は、数式処理（微積分、微分方程式、無限和、級数展開など）や関数電卓、関数やデータのプロットといった理論計算の補助として使う場面です。特に特殊関数の様々な操作について公式集を開かなくても良いところが非常に助けになっています。

また、値域が一目で分からない関数やデータであっても、一切設定なしで自動的に見栄え良くプロットしてくれるところが気に入っています。

数値が欲しい場合も、単位換算や物理定数の参照などをQuantity関数を用いて行うことができるので、確実に素早く計算できるのが良いです。 研究のまとめの段階では、これら計算に見出しなどをつけて整理し、必要な計算が一望できる論文作成の補助ノートとしても使用しています。

他の使用場面としては数値計算があります。特に重い数値計算の場合はRust言語などコンパイル型言語を用いて行っていますが、そうでない場合はMathematicaを使用する場合も多々あります。非常に多くの特殊関数が数値的に評価でき、数値積分、微分方程式、関数フィッティング、フーリエ変換といった多種多様な関数が備わっています。

他にはRust言語で書くプログラムのプロトタイプ作成のためによく使用しています。Rust言語はメモリ関連のバグがコンパイルの時点で取れるので、残るバグはプログラムとしては正しいが数式などを打ち間違えてしまっているような再現性のあるバグに限られます。

Mathematicaは大量の計算を走らせるには向きませんが、一つ一つの計算ステップや少ないデータ点の計算において素早く間違えずにプログラムすることができます。そのため、まずMathematicaでプログラムを書き、Rust言語でその結果を再現するようにプログラムすることで、長いプログラムであってもバグのないものを効率的に書き上げることができます。

Wolfram製品を使い始めたきっかけは？

大学院生の頃、研究室にサイトライセンスがあり、素粒子理論分野でよく使われるツールでもあったため使い始めました。

研究室のスタッフがMathematica入門講座を開いてくれたことも助けになったと覚えています。 その後、使用頻度が高かったためライセンスを購入して現在も使用しています。

Wolfram製品の魅力とは？

最も魅力的な点は非常に多くの関数が最初からサポートされていてクオリティが高いことです。他の言語ではライブラリを探すところから始めなければならない場合が多く、見つかってもソースコードを読まない限り（誤差が保証されている）定義域が分からない場合も多々あります。

Mathematicaでは実装自体はブラックボックスであることはよくありますが、使える定義域が広く、誤差が大きくなる場合には警告を表示してくれます。

次に、関数の引数や関数名が統一されていること、ドキュメントが充実していることがあります。特に、例を交えたグラフィカルなドキュメントは高く評価しています。また、数学的な定義などがきちんと書かれている点も大変助かっています。

今後の展望/製品機能への要望をおきかせください

少々テクニカルな内容ですが、改善して欲しい点がいくつかあります。

• 関数の級数展開はよく使用するのですが、特に無限遠点からの漸近展開について対応している関数が増えるとありがたいです。例えば（二変数同時のものですが）ベッセル関数のUniform Expansions (https://dlmf.nist.gov/10.41) のようなものができると良いです。また、超幾何関数についての展開は知られているかわかりませんが、よく出てくるのでこれが展開できなくて困ることが多いです。
• 大きな数値データをファイルに保存することがあるのですが、Save関数などではファイルサイズが大きくなってしまい、バイナリで保存できるhdf5ではどうしても対応しているデータタイプが限られてしまったり、データの削除が仕様上できなかったりします。他の言語でも読み書きできて、複素数などMathematicaでの数値データ形式が自然に扱えるバイナリ形式があったら良いなといつも思っています。

本事例作成に関し、庄司様 のご協力に感謝いたします。

(インタビュー：2024 年2 月)
※所属・役職は取材当時のものです。

関連リンク

• Institut “Jožef Stefan”