2025年3月28日
日本語
English
株式会社ヒューリンクス
TEL：03-5642-8384
営業時間：9:00-17:30
バージョンアップし続けるMathematicaとお付き合いして36年
常に時代とともにバージョンアップをし続け、LLMとの連携もとてもいい動きです。また表現力が素晴らしく、いろいろな可視化ができるので、とても分かりやすい魅力的な資料を作ることができます。
業務とご研究の内容について、お教えください
大学で超伝導応用工学の研究を行なっています。超伝導現象を扱うのには、電磁気学、熱力学、量子力学の深い知識が必要で、数式がたくさんでてきます。数式を導出して理解するという解析的なこともありますし、またよく使われている数式を数値的に解いていくこともあります。どちらもMathematicaにはとても助けられています。また、大学の学部生の演習課題にMathematicaを取り上げ、アニメーションを作製いただいています。面白い作品がたくさん生まれました。
Wolfram 製品をどのような場面で使用されていますか？
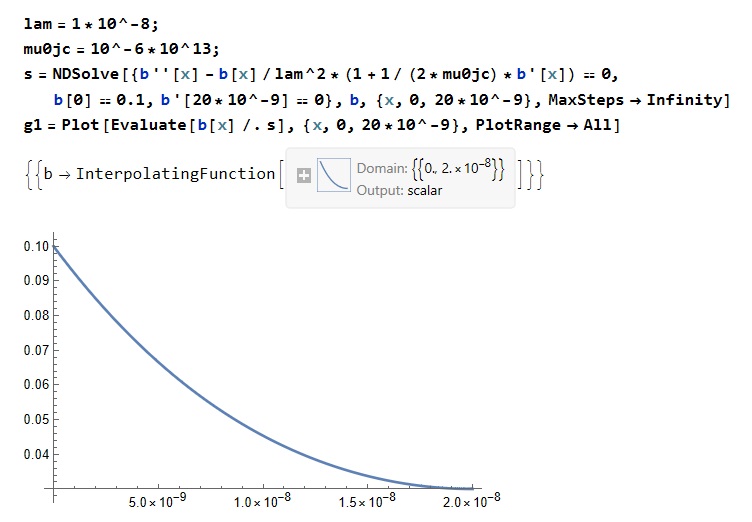
先日は2階の微分方程式を数値的に解くことを行なっていました。2階の微分方程式ですから境界条件は2つ必要です。普通はx=0における値とx=0における傾きを与えるのですが、x=0における値と超伝導体の中心x=dにおける傾きが0になるというちょっと工夫しないと解けない境界条件でした。それが自然に記述しただけで解けたので驚きました。これまではルンゲ・クッタ法でx=0における傾きを二分探索していたので、一気に楽になりました。このように以前は無理だったことがバージョンアップと共に解けるようになっているのはMathematicaの大きなメリットだと思います。
Wolfram 製品を使い始めたきっかけは？
すごく古いです。1988年に大学院生だった私は隣の情報工学科の友人のところでNeXT Cubeを触る機会があり、そこでMathematica 1.0を使いました。大型計算機でreduceというのを使ったことがありましたが、研究にはまったく使えませんでした。Mathematicaの衝撃はあまりに強くて、東京に行った折に八重洲の本屋で英書籍“The Mathematica”を買って夢中になって読んだ覚えがあります。
Wolfram 製品の魅力とは？
常に時代とともにバージョンアップをし続けていることです。今回もLLMを大いに取り入れています。とてもいい動きです。また、表現力が素晴らしくて、いろいろな形で可視化することができます。とても分かりやすい魅力的な資料を作ることができます。
今後の展望/製品機能への要望をおきかせください
今後、AIがより強力になるにつれて、MathematicaはAIとの連携が強く求められています。ChatGPTに微分方程式の画像を見せたら、ちゃんと解くことができました。でも正確かどうかは分からないです。Mathematicaであればもっと正確であるということが期待できるでしょう。より簡単な方法で使えるようになるのがMathematicaの発展に必要です。
Wolfram 製品の魅力とは？
常に時代とともにバージョンアップをし続けていることです。今回もLLMを大いに取り入れています。とてもいい動きです。また、表現力が素晴らしくて、いろいろな形で可視化することができます。とても分かりやすい魅力的な資料を作ることができます。
今後の展望/製品機能への要望をおきかせください
今後、AIがより強力になるにつれて、MathematicaはAIとの連携が強く求められています。ChatGPTに微分方程式の画像を見せたら、ちゃんと解くことができました。でも正確かどうかは分からないです。Mathematicaであればもっと正確であるということが期待できるでしょう。より簡単な方法で使えるようになるのがMathematicaの発展に必要です。
本事例作成に関し、小田部先生のご協力に感謝いたします。
(インタビュー：2025 年1 月)
※所属・役職は取材当時のものです。