Tempas 簡易マニュアル
- インストール
- MacTempasX の概要
- MacTempasX の実行
- コマンドメニュー
- Contextual メニュー
- ファイル形式
- 計算例
- 弱位相物体近似
- 階層構造の作成
- 幾何学的位相解析
- HRTEM画像から焦点を見つける
- ホルツ相互作用とサブスライス法
- 画像マッチングによる構造精密化
- 高分解能電子顕微鏡における最適および準最適フィルター
- 図
1. インストール
MacTempasX 本体はアプリケーションフォルダにドラッグすれば、インストールできます。その関連ソフト (ライセンスキーのドライバソフトウェア) は、インストーラをダブルクリックしてインストールして下さい。なおドライバソフトウェアは、インストール手順書に書かれている順番にインストールしないと、正常に動作しません。ドライバソフトウェアのインストールが済んだら、ハードウェアキー (ドングル) を USB ポートに差し込み、MacTempasX を起動して下さい。
ドライバソフトウェアのインストール順序
- Eve3Framework
- SentinelKeys32Framework
- SentinelSystemDriver.pkg (PPC Mac では不要)
MacTempasX は、ハードウェアキーによってライセンス情報の管理を行っております。MacTempasX 本体は複数のコンピュータにインストールしておくことができますが、実際に起動できるのはハードウェアキーを差したコンピュータだけとなります。ハードウェアキーを差していない場合は、デモモードでの動作となります。
MacTempasX を初めて起動すると、ユーザー情報を登録するためのウィンドウが表示されます。お名前と所属を入力して、Set ボタンをクリックして下さい。
2. MacTempasX の概要
3つのシミュレーションステップ
HRTEM 位相コントラスト画像のシミュレーションは、構造計算、散乱プロセス、イメージ合成の3つの計算に分割することができます。MacTempasX は、Calculate メニューコマンドを使って、それぞれの独立した計算を呼び出すことができます。
- Full Calculation
開始ポイントからイメージ合成までのすべての計算を行うコマンドです。 - Projected Potential
結晶の投影ポテンシャル、すなわち単位格子の大きさ、対称性、原子の位置や占有率、温度因子など結晶構造データから電子の分布状態を計算します。 - Exit Wavefunctions(s)
出射面における電子波動場を生成するコマンドです。電子顕微鏡の加圧電圧、試料の厚さと傾斜のデータ、投影ポテンシャルを用いて計算します。計算アルゴリズには、マルチスライス近似方式を採用しています。 - Image(s) normal calculation
電子顕微鏡像の強度を計算します。対物レンズの位相変化、分解能を制限する収差の影響を、焦点外し、球面収差、入射ビームの収束、焦点外しの範囲、対物絞りの位置とサイズなどのパラメータを使って計算します。 - Image Plane Wavefunctions(s)
電子顕微鏡像の波動関数を計算します。出射面における電子波動関数のフーリエ変換/逆フーリエ変換を、コントラスト伝達関数 (CTF) を使って評価しています。顕微鏡像の波動関数は、電子ホログラフィによって見つかった電子波動関数との比較されます。
Calculate メニューの残りのコマンドは、メニューの章で説明します。
結晶の投影ポテンシャル (Projected Potential コマンド) の計算では試料の構造のみを考慮しますが、電子波動場 (Exit Wavefunctions(s) コマンド) の計算では試料と電子波動の相互作用を取扱い、Image(s) normal calculation コマンドでは電子顕微鏡のレンズシステムを考慮したシミュレーションを行います。一度シミュレーションを実行したら、以後のシミュレーションではすべてを再計算する必要はありません。電子顕微鏡のパラメータ (電圧を除く) を変えただけなら、投影ポテンシャルおよび出射面の波動関数の計算には何の影響もありません。結晶構造像を再描画するだけで済みます。電子顕微鏡の電圧、または試料の厚さ・傾斜を変更した場合には、投影ポテンシャルの計算には影響はありませんが、出射面の波動関数と結晶構造像は再計算する必要があります。試料の構造を変更した場合は、もちろんすべての再計算が必要となります。
生成されるファイル
MacTempasX は、シミュレーションの過程で様々なファイルを生成し、保存します。主要な 6つのファイルは以下の通りです。
- <structurename>.at
シミュレーションを実行するのに必要な結晶構造および電子顕微鏡のすべての情報を保存します。これらは、ユーザーの入力データ、使用したデータファイルが元になっています。<structurename> には、結晶構造を作成するとき入力した構造の名称が使用されます。ファイル形式はテキストファイルです。 - <structurename>.pout
<structurename>.at ファイルに保存された情報を使用した、投影ポテンシャルの計算結果が保存されます。電子ビーム方向の投影ポテンシャルが保存されています。ファイル形式は、REAL(4) 型のバイナリファイルです。最初の 80 バイトにはレコード情報、つぎにデータが保存されます。第 1行目は、結晶構造像の底辺のデータが記述されます。これは、MacTempasX の座標軸は、画像および単位格子の左下が原点になるからです。データがインポートされている場合は、画像が反転して表示されます。 - <structurename>.mout
<structurename>. pout と <structurename>.at ファイルのデータを使って、マルチスライス計算を行った結果が保存されます。1つ以上の試料の厚さで計算した出射面の波動関数が含まれます。ファイル形式は、<structurename>.pout と同じ構造のバイナリファイルですが、実数と画像のバイナリデータが含まれています。データは 80 バイト目から始まり、複数の出射面波動関数が保存できます。 - <structurename>.iout
<structurename>.at ファイルの電子顕微鏡パラメータを出射面波動関数に与えて結晶構造像を作成した結果が保存されます。1つ以上の画像が含まれています。ファイル形式は REAL(4) 型のバイナリファイルで、80 バイト目からデータが始まります。 - <structurename>.hout
シミュレーションした結晶構造像の代わりに、投影面における電子波動関数の計算結果が保存されます。ファイルには、実数と画像のバイナリデータが含まれ、80 バイト目からデータ領域となります。複数の電子波動関数を保存できます。 - <structurename>.aout
試料の各スライス面における回析波の振幅が保存されます。回析波はユーザーが選択でき、試料の厚さの関数としてプロットします。
上記のファイルに加えて、印刷に使用するためのフィアル (めったに印刷されることはありませんが) が作成されます。 - <structurename>.p_prnt
Projected Potential メニューコマンドで、<structurename>.at の設定を使って投影ポテンシャルを計算した結果の印刷データです。 - <structurename>.m_prnt
Exit Wavefunctions(s) メニューコマンドで、<structurename>.at の設定を使って <structurename>.pout のデータを計算し、出射面の波動を生成した情報が含まれます。すなたち、マルチスライス計算の印刷データです。
3. MacTempasX の実行
入力データの作成
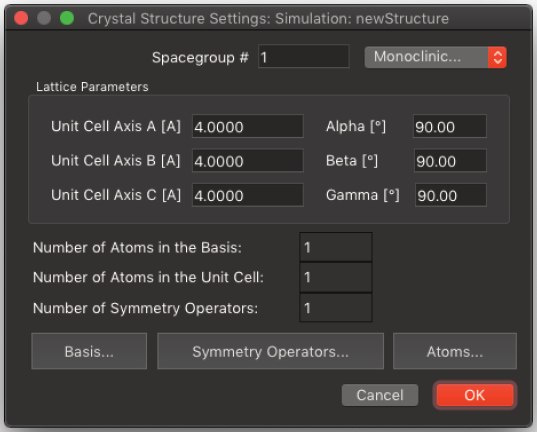
シミュレーションを実行するために最初のステップは、入力ファイルの作成です。これは、File|New Structure File… メニューコマンドで実行することができます。このコマンドを実行すると、立方晶のデフォルト設定値がダイアログに標示されます。作成したい構造のテンプレートとして使用して下さい。
A, B, C, alpha, beta, gamma
- 単位格子の基本ベクトルの長さはオングストローム (Å) 単位で、格子定数の角度は ° で表します。MacTempasX は、空間群に基づいて格子定数を自動的に設定します。同様に格子の他のパラメータも自動的に設定されます。なお、立方晶を選択した場合は、A=B=C となります。
Spacegroup #(Int. Tables)
- MacTempasX は、空間群の番号または記号 (International Tables for Crystallography に基づく) を選択すると、230 ある空間群のどれかの対称操作が実行されます。Space Group のポップアップメニューをクリックすると、最初に結晶構造の種類 (たとえば六方晶や立方晶など) を選択して、230 の空間群の 1つを指定します。空間群記号または番号をクリックして選択することもできます。

可能な場合は、空間群の追加設定を行うことができます。特に空間群を指定しない場合は、対称操作が x, y, z だけの空間群 P1(1) を使用して下さい。対称操作のダイアログを開くと、追加の対称操作が指定できます。
Show (# of atoms in Basis)
- このボタンをクリックすると、基本構造 (非対称単位) を構成する原子のダイアログが開きます。
# of Atoms in the Basis
- この番号は、単位格子の中の基本構造 (非対称単位) を構成する原子の番号です。対称操作を行ったとき、基本構造は単位格子の中のすべての原子の位置を決定します。この番号はデータが入力される度にプログラムが再計算を行い、ユーザー自身で変更することはできません。
Show (# of Symm. Ops.)
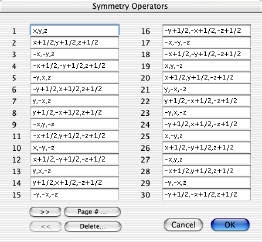
- 空間群を決定すると、対称操作は自動的に生成されます。このボタンをクリックすると、対称操作の一覧が表示されます。
Show (# of Atoms in UCell)
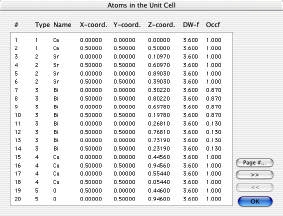
- 基本構造である原子に関して対称操作を実行すると、単位格子の原子が自動的に生成されます。各原子の番号が与えられ、Show ボタンをクリックすると単位格子を構成する原子の一覧が表示されます。
# of different atoms
- この値は、試料を構成する原子の種類数です。元素番号またはデバイワラー因子によって、原子が区別されます。MacTempasX によって正確な値が計算・表示されます。
Zone-axis
- 実空間の軸方向に対して試料がなす方向 (晶帯軸) です。
Num slices per cell
- ビーム方向に大きな間隔で繰り返しがある単位格子の場合、Gmax が最適な値ならば、選択したスライスの厚さの逆数のポイントで、エワルド球が試料上側レイヤーのラインに接します。この場合、MacTempasX はさらにそのスライスを2つ以上のサブスライスに分割することができます。このとき、Options|Slice Method… メニューコマンドの設定によってつぎのようになります。2-D calculation が選択され、かつ sub-divide のチェックボックスが OFF の場合は、n スライス分の計算を行って、晶帯軸方向の単位格子の投影ポテンシャルを求めます。2-D calculation が選択され、sub-divide チェックボックスが ON の場合は、各サブレイヤー内の原子を使って各スライスのポテンシャルを計算し、晶帯軸方向の単位格子の投影ポテンシャルを求めます。3-D calculation が選択された場合は、単位格子内のすべての原子を最適な n スライスに分け、単位格子の投影ポテンシャルを求めます。
Gmax
- マルチスライス回析の計算では、散乱ベクトルの最大値 (1/Å) が使用されます。この値は、散乱プロセスにおける回析ビームの絞りに相当します。すべての主要なビームの相互作用が含まれるように、十分な大きさが必要です。デフォルト設定値は、2.0 です。MacTempasX は、マルチスライス計算でのエイリアシングを避けるために、Gmax に対して 2回位相格子の係数を適用しています。
Thick.(beg.inc.end)
- 試料の厚さは、初期値、増分、終値が入力できます。すべてオングストローム単位です。数値は、上端、ステップ数、下端で入力します。たとえば「100 50 250」の場合は、100Å から 250Å まで 50Å 刻みで (すなわち 4つの厚さで) MacTempasX は出射波動を計算します。
Store Ampl./Phases|Set…
- このボタンをクリックすると、試料の厚さの関数として強度と位相変化をプロットするために、回析波を選択できます。追跡する反射は、hkl 値を入力して指定します。追跡できる反射波は、10 です。
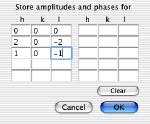
Cent. of the Laue Circle
- 試料の傾斜は、ラウエの円の中心を、投影された単位格子の2次元逆空間の h と k 値で指定します。傾斜角と方位角を代わりに指定する (Eq. Tilt [mrad] & angle °) こともできます。新たな設定値と逆空間格子との関係は、データファイル <structurename>.p_prnt に保存されます。
Type of Absorption
- 吸収は、仮想の投影ポテンシャルを想定することで、計算されます。
Microscope Name
- 電子顕微鏡の種類によって、顕微鏡画像のパラメータが異なります。ポップアップメニューには、未定義の顕微鏡のほか定義済みの電子顕微鏡がリストされています。定義済みの顕微鏡を選択すると、MacTempasX は対物レンズの球面収差係数 Cs (mm) 、色収差に基づく焦点のガウス拡散の半値 Δ (Å) 、入射ビームの収束 θ (mrad) の値を設定します。電子顕微鏡の種類がわからない場合は、それぞれの値を入力します (ユーザー定義の顕微鏡の設定の仕方は、後述します) 。
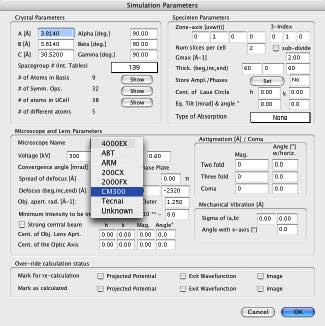
Voltage
- 電子顕微鏡の加速電圧 (kV) 。
Defocus (beg.inc.end)
- 対物レンズのボケは、ボケの具合を負の値 (アンダーフォーカスの値:Å) で入力します。試料の厚さと同じように、上端、下端とステップ幅で入力します。
Minimum Intensity to be included in the lens
- 電子ビームの計算の際、強度のカットオフ値として指定します。通常はデフォルト設定値で十分で、計算時間もかかりません。しかし、欠陥を含む大きな結晶構造の場合は、拡散する散乱ビームが弱くなるため、カットオフ値を小さく設定しないと正しいコントラストが得られません。
Strong Central Beam
- このチェックボックスが ON になっている場合は、線形の区間のみで結晶構造像の強度を計算します。通常は線形ではない区間も含めて強度を計算します。
Cs
- 対物レンズの球面収差 (mm) 。
Convergence Angle
- コンデンサレンズが絞った入射電子が作る円錐の拡がり角 (mrad) 。
Spread of defocus
- 画像をなす電子のエネルギ分布と、対物レンズの色収差によって生じるボケの実際の拡がり (Å) 。
Obj. apert. rad
- 対物絞りの半径 (1/Å) 。内側と外側の両方が設定できます。通常、内側の絞りは 0 です。
Cent. of Obj. Lens Aprt
- 対物レンズの絞りの中心は、ラウエの円の中心と同じように、単位格子の2次元逆空間の h と k で設定されます。傾斜角と方位角を代わりに使用することができます。
Cent. of the Optic Axis
- 電子顕微鏡の光学軸の中心は、ラウエの円や絞りの中心と同じように、単位格子の 2次元逆空間の h と k で指定します。
Two fold (Astigmatism)
- 対物レンズと x 軸角度の 2回非点収差 (Å) 。
Three fold (Astigmatism)
- 対物レンズと x 軸角度の 3回非点収差 (Å) 。
Coma
- 対物レンズと x 軸角度のコマ収差 (Å) 。
Mechanical Vibration
- 電子顕微鏡の微少な振動をシミュレートします。諸条件に関係なく、実際の試料ではありえない画像が表示されることがよくあります。これは、電子顕微鏡の振動や、その他の条件変動によって生じた画像の劣化が原因であると考えられます。そこで、微少な機械的振動を考慮した電子顕微鏡画像をシミュレートします。晶帯軸に対する楕円の傾きと、その 2つの垂直軸方向の振幅で異方性振動を与えることができます。
4. コマンドメニュー
Tempasの多くの機能は、Tempasのメニューから実行されます。
これにはマルチスライス計算も含まれます。さらに、ほとんどのオプションはメニューから設定されます。以下は、現在利用可能なメニューの一覧とその機能の説明です。
4-1. Fileメニュー
4-2. Editメニュー
4-3. Optionsメニュー
4-4. Commandsメニュー
4-5. Parametersメニュー
4-6. Calculateメニュー
4-7. Tablesメニュー
4-8. Quantitativeメニュー
4-9. Processメニュー
4-1. Fileメニュー
New Normal Structure…
- 新しい構造ファイルを作成します。入力前にファイル名を入力するように促されます。
一意の構造名を入力すると、プログラムは拡張子.atを付加します。
ファイル名に拡張子を除いてピリオドが含まれないように注意してください。
これは、すべてのパラメーターにデフォルト値を設定した新しい構造を作成します。
デフォルトの構造は、基底に1原子と1つの対称性演算子を持つ単斜晶構造です。結晶単位格子を変更するには、パラメーターメニューから「結晶構造を表示…」を選択します。入力内容を作成したい構造に合わせて変更してください。
New Layered Structure…
- 新しいレイヤードシミュレーションファイルを作成します。入力を行う前に、ファイル名を入力するように促されます。一意の構造名を入力すると、プログラムは拡張子 .lay を付加します。
レイヤード構造は、事前に計算された投影ポテンシャルのシーケンスから構成される点が特徴です。
したがって、レイヤードシミュレーションファイルには原子位置は含まれません。層状「構造」において意味を持つのは、格子定数AとB、およびガンマのみです。
「Set Phasegratings」と「Define Stacking」のボタンを使用して、異なる投影ポテンシャルを選択し、試料全体を構成するシーケンスを定義します。
- 「Set Phasegratings」は、事前に計算された「pout」ファイルを選択するための設定を行います。
これらのファイルはすべて、同じ格子定数aとbを持つ必要があります。 - 「Define Stacking」は、試料を構成するフェーズグレーティングファイルのシーケンスを設定するのに役立ちます。
これにより、右図のダイアログが表示されます。
Open Structure File…
- 既存の構造ファイルまたはレイヤードファイルを開きます。標準のファイル開くダイアログが表示され、
「TEXT」形式で拡張子が「.at」または「lay」のファイルのみが選択可能として表示されます。
表示ウィンドウの名前は、現在の構造の名前を反映して変更されます。
Recent Simulation Files Menu
- 最近開いたシミュレーションのリストを表示し、ユーザーが開くファイルを選択できるようにします。
Close
- 現在選択されているファイル、画像、またはウィンドウを閉じます。
Save…
- 現在のアクティブウィンドウに応じて、現在の情報を保存します。
アクティブウィンドウがシミュレーションウィンドウの場合、構造ファイルを保存する操作になります。
Save As…
- 現在の構造情報または画像を保存します。シミュレーションの場合、拡張子を付け加えないでください。Tempasが自動的に適切な拡張子を選択します。
- 画像メニューに表示されている次の2つのメニューコマンドは、ライセンスの一部としてスクリプトモジュールが有効化されている場合のみ表示されます。
Open Image…
- 画像を開きます。現在サポートされている画像はTIFFファイルとバイナリファイルです。
RGB TIFFファイルと圧縮TIFFファイルはサポートされていません。
バイナリファイルは整数型または浮動小数点型(実数または複素数)で、異なる長さやバイト順序を持つことができます。
Recent Images Menu
- 最近開いた画像のリストを表示します。
New Image…
- 指定したサイズと内容の新規画像を作成します。
Image Stack Menu
- 画像のシーケンスから画像スタックを作成できます。
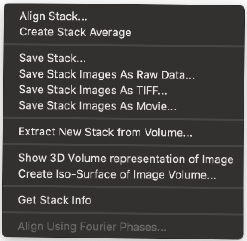
画像スタックがImageWindowでアクティブになっている場合、メニューの操作は画像スタックに対して実行されます。 - 画像スタックには、それに付随するコンテキストメニューも表示されます。
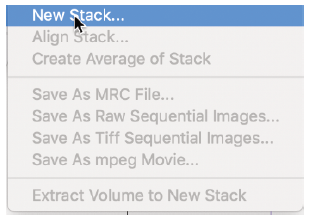
Print…
- アクティブなウィンドウに対してOSの印刷コマンドを実行します。
4-2. Editメニュー
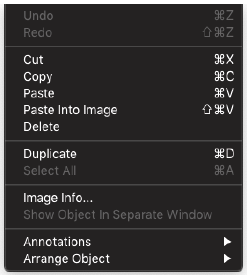
Undo, Redo
- 直前の操作を元に戻す/やり直す。これらの操作は現在Tempasでは機能しません。
Cut
- 選択したオブジェクトまたは選択ツールで選択した範囲を切り取ります。
Copy
- 選択範囲または選択されたオブジェクトをコピーします。。
Paste
- 貼り付けバッファの内容をディスプレイウィンドウに貼り付けます。貼り付けのソースは、他のアプリケーションから切り出した画像またはTempasの切り取り/コピーコマンド経由の画像です。
オブジェクトが画像の場合、現在選択されている場合はディスプレイウィンドウに、選択されていない場合は別々の画像ウィンドウに貼り付けられます。
Paste Into…
- 貼り付け先はアクティブなウィンドウによって異なります。通常、貼り付け先はクリップボード内のオブジェクトを現在アクティブなシミュレーション表示ウィンドウに配置します。また、アクティブな画像ウィンドウに画像を配置することもできます。
Delete
- 選択ツールで選択したオブジェクトを消去します
Duplicate
- 複製は選択したオブジェクトを複製し、オブジェクトのコピーを作成して表示します。
Select All
- 表示ウィンドウ内のすべてのオブジェクトまたは画像全体を選択します。
Object/Image Info…
- 編集可能なオブジェクトの場合、選択したオブジェクトに関連する情報を表示します。
表示されるダイアログボックスは、編集中のオブジェクトの種類によって異なります。
Show Object in SeparateWindow
- シミュレーションウィンドウ内のオブジェクトを、そのオブジェクト専用のウィンドウに表示します。オブジェクトの表示方法に関する追加のオプションが利用可能になる場合があります。
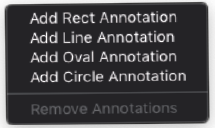
Annotations
- 画像上に配置する注釈を作成します。
Arrange Object
- アクティブなシミュレーション表示ウィンドウ内のオブジェクトを、スタック順序に基づいて配置します。
4-3. Optionsメニュー
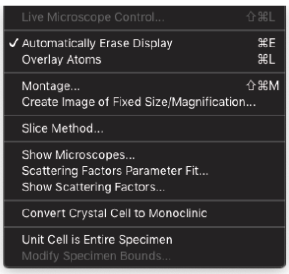
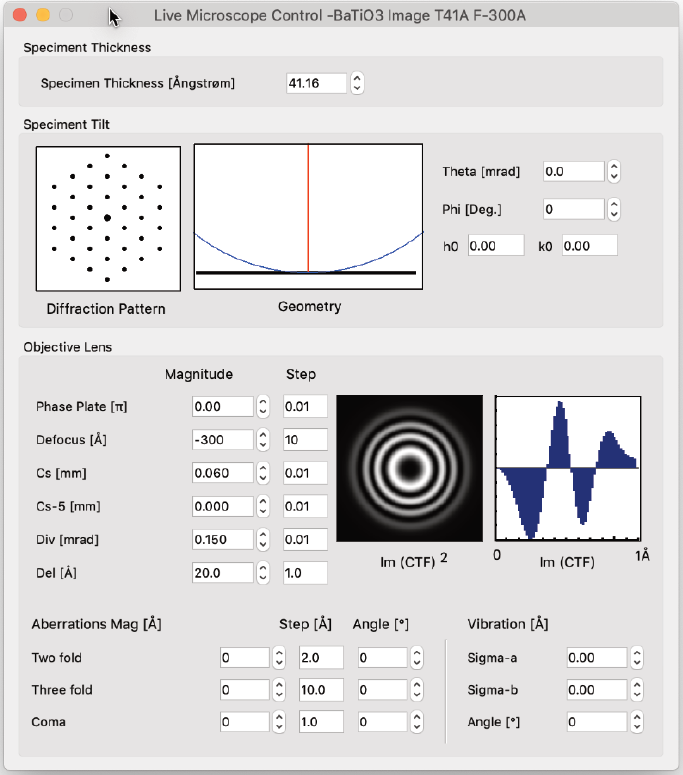
Live Microscope Control…
- 計算された画像が選択されている場合、このコマンドを実行すると、この画像の計算パラメーターを変更するためのインタラクティブウィンドウが表示されます。
パラメーターの変更は、計算時間が合理的な範囲内であれば、リアルタイムで反映されます。
Automatically Erase Display
- アクティブなシミュレーション表示ウィンドウ内の以前のコンテンツが、新しいオブジェクトがウィンドウに追加された際に消去されるかどうかを切り替えます。
Overlay Atoms
- 設定すると、原子の位置が画像の上に円として描画されます。円は原子の半径にスケールされ、色は該当する原子種に設定された色になります。
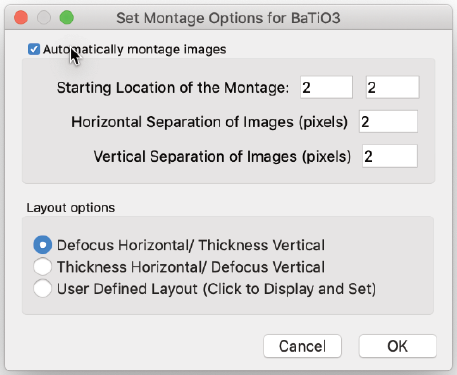
Montage…
- ダイアログボックスを表示し、ユーザーが画像の自動モンタージュ、画像の配置位置、画像間のピクセル数を設定できます。
Slice Method…
- ユーザーが、逆空間の3次元(l)について和を計算することで、投影ポテンシャルの3次元計算を行うオプションを選択できます。
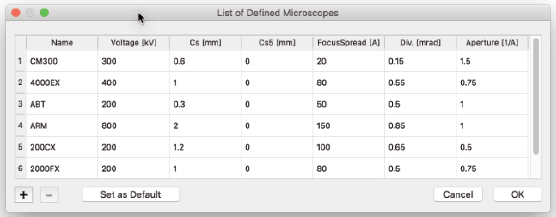
Show Microscopes…
- ユーザーにTempasが認識している顕微鏡を表示するダイアログを表示します。
認識されている顕微鏡に割り当てられたデフォルトパラメーターはユーザーが変更でき、新しい顕微鏡をTempasに認識させることができます。
追加の顕微鏡を追加したり、既存のものを削除したりできます。必要に応じて、選択した顕微鏡をデフォルトの顕微鏡として設定できます。
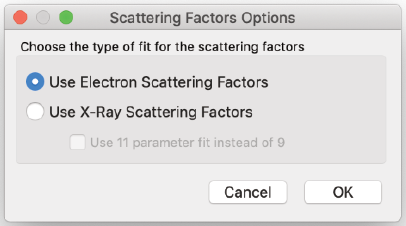
Scattering Factors Parameter Fit…
- Tempasは、電子散乱係数には8パラメーターフィット、X線散乱係数には9パラメーターフィットを使用できます。メニュー項目のテキストは現在の設定を反映します。
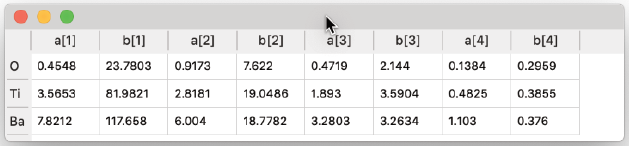
Edit Scattering Factors…
- 適合パラメータのテーブルを表示します。各項目は編集可能です。
Convert Crystal Cell to Monoclinic
- この操作は、現在の結晶構造を対称性群P1(単一の対称性演算子「x,y,z」からなる)に変換します。構造内のすべての原子は、結晶格子の基底に移動されます。構造自体は変化しませんが、基底に対しては単位演算子以外の対称性演算子が適用されなくなります。
Unit Cell is Entire Specimen
- このオプションが設定されている場合、計算では単位格子を非反復構造として扱い、試料全体が単一の単位格子で表され、試料の厚さが単位格子の厚さとして設定されます。
Modify Specimen Bounds
- 単位格子が試料全体である場合、この機能によりユーザーは指定されたゾーン軸方向における格子の境界体積をトリミングできます。
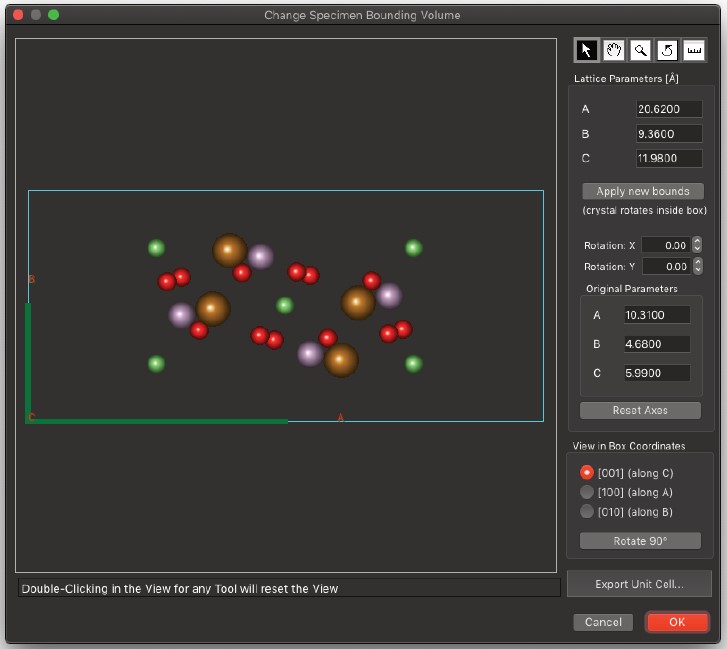
4-4. Commandsメニュー
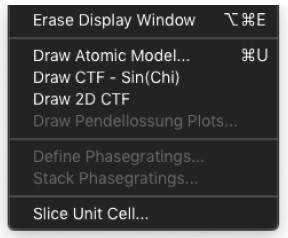
Erase DisplayWindow
- ディスプレイ ウィンドウを消去します。
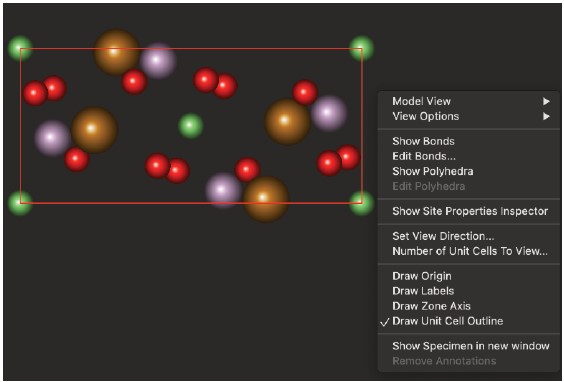
Draw Atomic Model…
- ダイアログ ボックスを表示し、ユーザーは任意の方向(パースペクティブ ビューを含む)から元の単位格子または変換された単位格子を選択して表示できます。変換された単位格子は、Tempas がマルチスライス計算で使用する単位格子に対応しています。
電子が「見る」ようにセルを表示するには、変換された(新しい)単位格子を001方向で表示する必要があります。表示方向は実空間単位格子軸の単位で指定されます。また、指定した方向での材料の断面を表示することもできます。ダイアログボックスで、2方向の視野角をÅ単位で指定できます。
- クリスタル/標本モデルには、モデルを表示する際の機能の一部を制御するコンテキストメニューがあります。
モデルを選択した状態で右クリックすると、以下のコンテキストメニューが利用可能です。
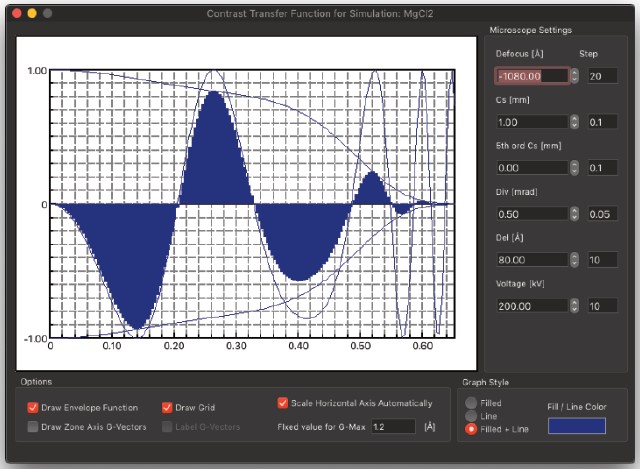
Draw CTF -Sin (chi)
- 現在の顕微鏡のコントラスト転送関数(CTF)を描画します。
元の顕微鏡の値は構造データから取得されますが、ユーザーは画像計算に使用される値とは独立して、CTFに関連する値を変更できます。CTFをクリックすると、CTFの値と解像度を表示するバーが表示されます。このバーはマウスと共に移動します。
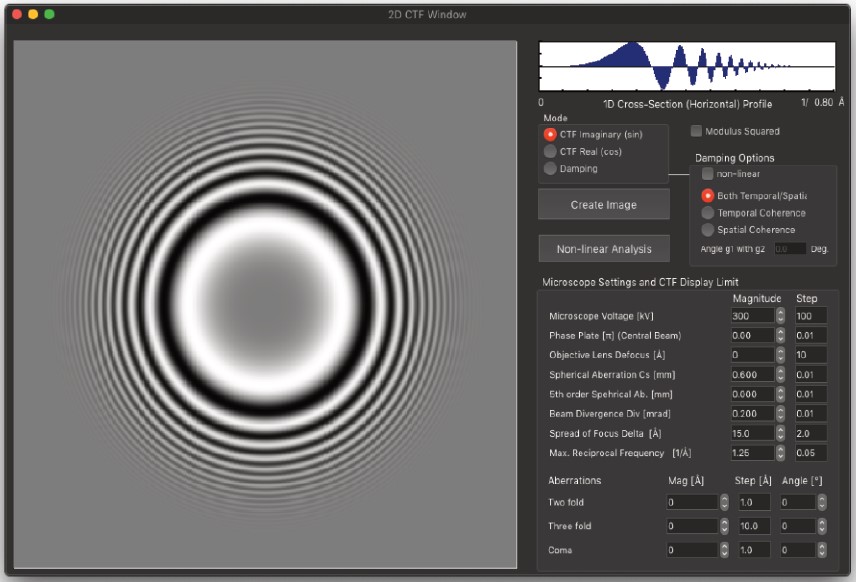
Draw 2D CTF…
- 線形および非線形画像の両方に対して、2次元コントラスト転送関数のさまざまな表現を描画します。
非線形画像の寄与は、非線形解析ボタンを通じて詳細に分析できます。
非線形画像の寄与は、非線形解析ボタンを通じて詳細に分析できます。
Draw Pendelløssung Plots…
- ユーザーが試料の厚さに対する振幅と位相のグラフ化用に回折ビームのセットを保存するように選択した場合、このダイアログボックスが表示され、ユーザーはグラフ化条件を設定できます。振幅または強度をプロットするだけでなく、回折ビームの位相をプロットすることもできます。
各反射を個別にプロットするか、複数の反射を同じプロットに重ねて表示することも可能です。値をプロットする代わりに、値をファイルに書き出して、さらに操作や確認を行うこともできます。
Define Potentials…
- これにより、ユーザーはレイヤード構造で使用するポテンシャルを指定できます。レイヤード構造の作成方法の詳細な手順については、第9章を参照してください。
Stack Potentials…
- これにより、ユーザーはマルチスライス計算で使用するポテンシャルの順序を指定できます。これは層状構造にのみ適用されます。層状構造の作成方法の詳細な手順については、第9章を参照してください。
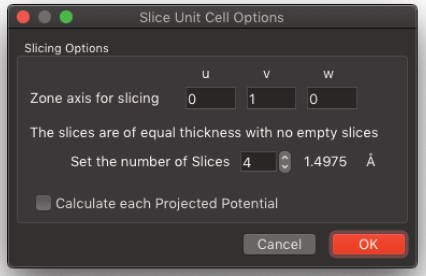
Slice Unit Cell…
- このオプションを使用すると、構造を層状構造計算で使用するための独立した層に分割できます。スライスに垂直な方向とスライスの数を指定する必要があります。
4-5. Parametersメニュー

Show All Simulation Parameters…
- このオプションを選択すると、現在のシミュレーション条件を表示するダイアログ ボックスが表示されます。
これらの値は、ファイル メニューの「新規…」コマンドに入力された値から取得されます。
これらのパラメーターを変更することで、新しいシミュレーションを実施できます。
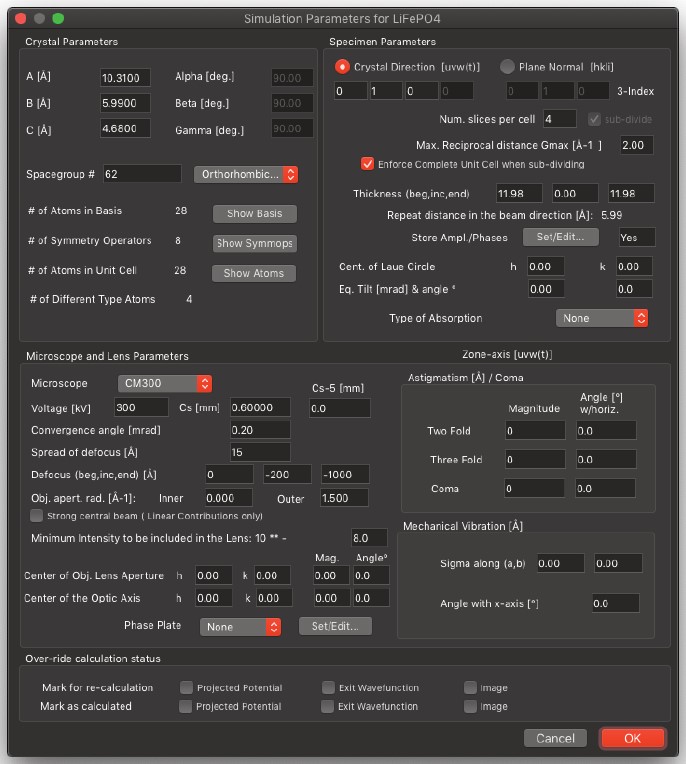
Show Crystal Structure…
- 現在使用中の結晶構造のすべてのパラメーターを新しいダイアログウィンドウに表示します。
格子パラメーター(A、B、C軸の長さ)および関連する角度(アルファ、ベータ、ガンマ)を表示します。さらに、単位格子のモチーフを構成するすべての原子、空間群、および空間群を構成する対称操作子へのアクセスを提供します。
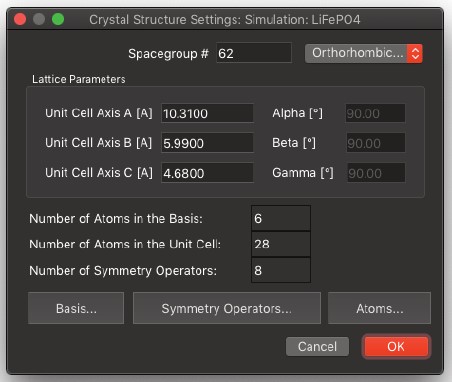
Show Specimen Parameters…
- 試料に関連するすべてのパラメーターを表示します。試料は、電子ビームの方向に基づいて結晶単位格子から導出されます。
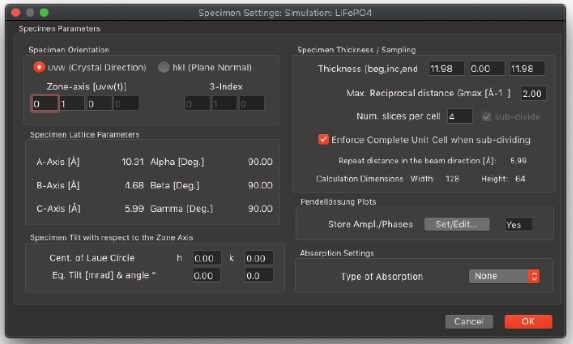
Show Microscope Parameters…
- これにより、空間群に関連付けられたか、またはユーザーが手動で入力した対称性演算子のリストが表示されます。対称性演算子は編集可能であり、リストに新しいものを追加したり、既存のものを削除したりすることができます。
4-6. Calculateメニュー
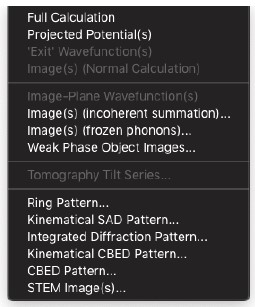
このメニューの有効なコマンドは、現在の計算状態に依存します。
現在のパラメーターセットでシミュレーションが既に実行されている場合、
有効なコマンドは表示されません。パラメーターに変更が加えられた場合、
またはファイルが新規に作成された構造ファイルの場合、
実行が必要なサブプログラムを示すコマンドが
有効に表示されます。
Full Calculation
- シミュレーションパラメーターの最後の変更点から開始し、マルチスライス計算を終了まで実行したい場合、このコマンドを使用します。
Projected Potential
- 投影ポテンシャルのみを計算します。
計算終了時、ポテンシャルはシミュレーションウィンドウに2×2単位セルの画像として表示されます。非常に大きな単位セルの場合、1×1単位セルの画像のみが表示されます。
Exit wave functions(s)
- 出口波動関数のみを計算します。
計算終了時、出口波動関数はシミュレーションウィンドウに2×2単位格子を表示する画像として表示されます。非常に大きな単位格子の場合は、1×1単位格子画像のみが表示されます。
Image(s) (normal calculation)
- 部分的相関エンベロープ関数とレンズコントラスト転送関数を使用して画像を計算します。
画像は、他の計算結果と同様の形式で表示されます。もし計算が厚さ方向と焦点方向のシリーズを含む場合、出力は各厚さごとに1つの画像スタックからなる複数の画像スタックの形式となり、各スタックには焦点値の数だけ画像が含まれます。
Image-Plane wave functions(s)
- 画像平面における波動関数を計算します。これは、ホログラフィーを使用して再構築されるものと同等です。
Image(s) (incoherent summation)…
- 画像を計算しますが、異なる入射方向と異なるエネルギーから生じる不整合な画像を合計します。
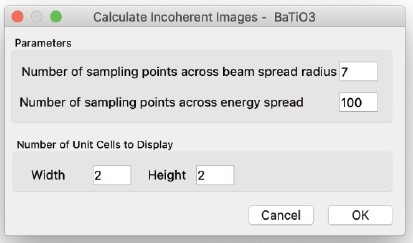
Image(s) (frozen phonons)…
- 異なる原子配置から計算された画像を、原子のランダムな変位に応じてデバイ・ウォラー因子に従って合計することで、画像を計算します。
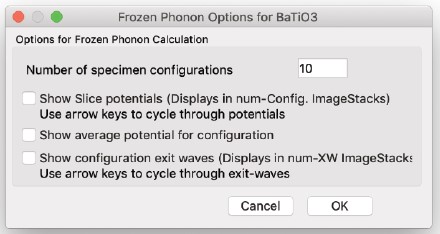
Weak Phase Object Images
- これは、理想的なシェッツァーレンズの場合に生成される画像の計算を可能にする独立したモジュールであり、弱い位相オブジェクト近似の有効性を検証するためのものです。“WPO”計算の詳細な説明は、他の場所でより詳しく説明されています。
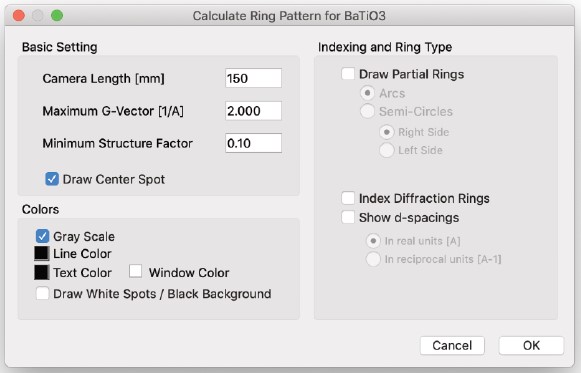
Ring Pattern…
- リングパターンは、特定のgベクトルに対して予想される散乱の強度に応じて円の強度を設定します。
- 「強度」は構造因子に比例します。構造因子は、基本的に静電ポテンシャルのフーリエ変換に対応する周波数のフーリエ変換振幅です。
Kinematical SAD Pattern…
- 運動学的SADパターンはリングパターンと同じ計算を行いますが、円板のサイズはgベクトルの構造因子に比例します。
- gベクトルは、結晶材料の場合、結晶の周期性に対応する周波数成分です。
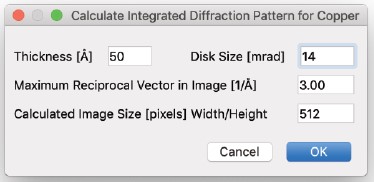
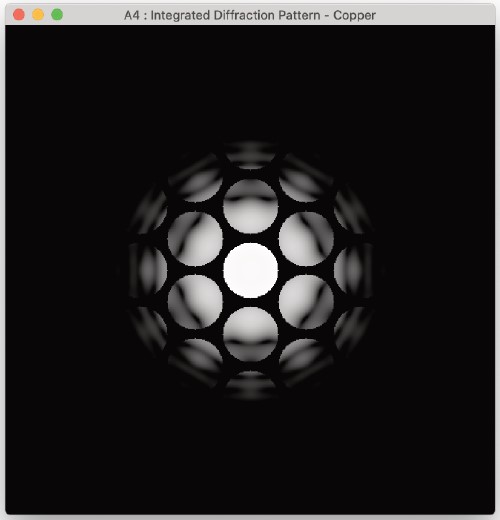
Integrated Diffraction Pattern
- 各入射電子方向の錐体内の各傾斜角度における強度を合計することで、回折パターンを計算します。
下記のパラメーターに基づいて計算されたパターンは、右図のようになります。
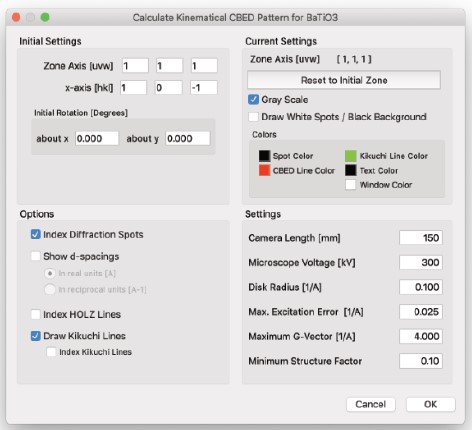
Kinematical CBED Pattern…
- 指定された入力パラメーターに基づいて、運動学的CBEDパターンを計算します。
ディスクのサイズ(収束角)は、中央のディスクの周縁をドラッグすることで調整できます。
ディスクの濃淡は、指定された散乱ベクトルの構造因子によって決定され、中央のディスク内のHOLZ線は、線の幾何学的記述から計算されます。
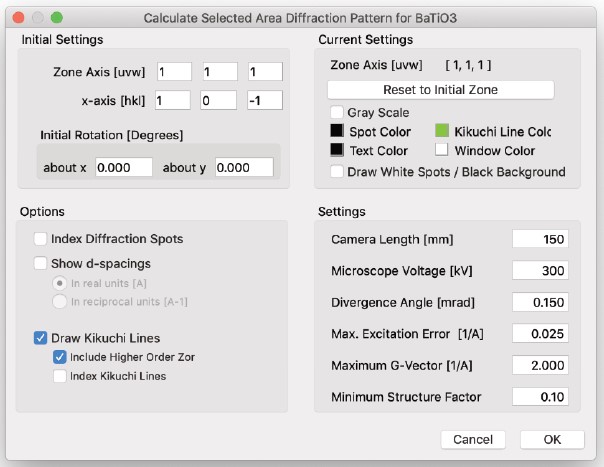
CBED Pattern…
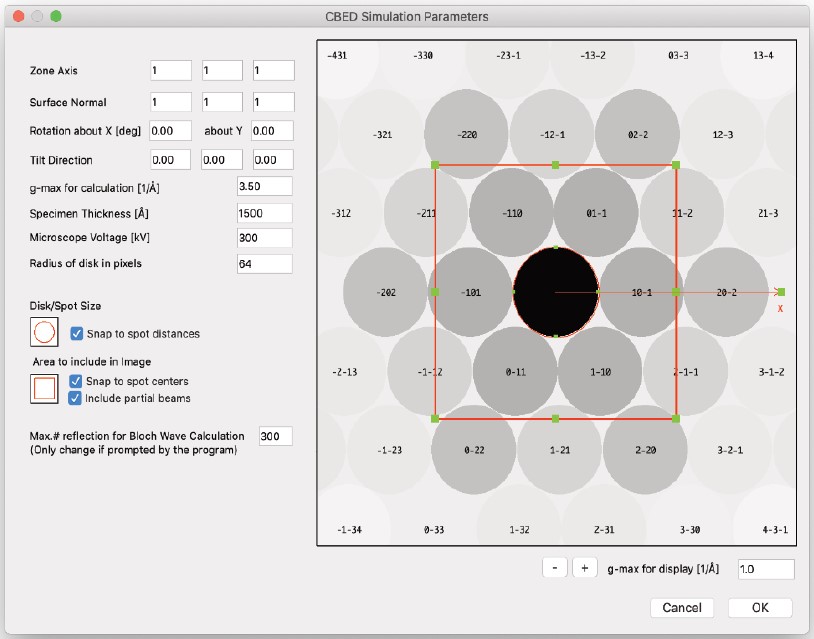
- 指定された入力パラメーターを使用して、Bloch波近似を用いて動的CBEDパターンを計算します。
パターンのx軸は、x軸の矢印の緑色の選択矩形を回折スポットにドラッグすることで設定できます。パターンは回転し、選択されたスポットがパターンのx軸に沿うように調整されます。
計算された画像に表示されるパターンの部分は、赤色の「Image」矩形内に含まれる部分です。
この矩形はサイズを変更したり、ドラッグして移動させることができます。スポットサイズ(収束角)は、中央のディスクのサイズを変更することで調整されます。

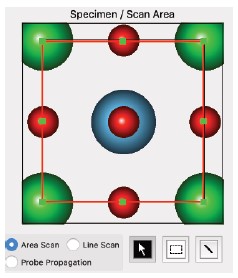
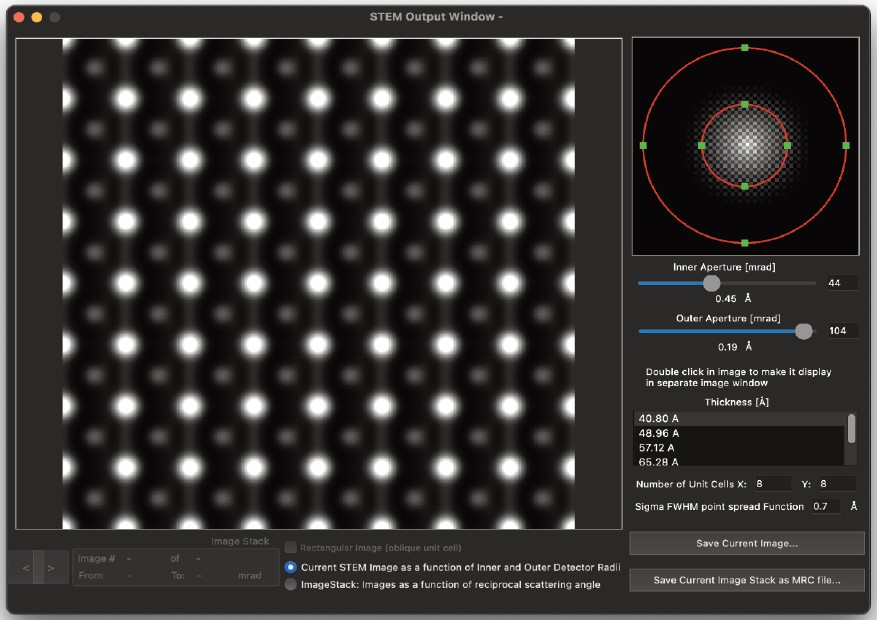
STEMImage…
- 指定された入力パラメーターに基づいてSTEM画像を計算します。
電子プローブの各位置に対してマルチスライスシミュレーションを実行し、その位置における画像の輝度は、環状検出器内に収まる積分輝度です。
右図のダイアログには、STEM画像の計算を決定する入力パラメーターが表示されます。 - 以下の2つのダイアログセクション内のすべてのパラメーターは、プローブとその形状を定義します。アベレーションは明らかな入力パラメーターであり、顕微鏡の条件を表します。理想的な条件下では、アベレーションはすべてゼロです。
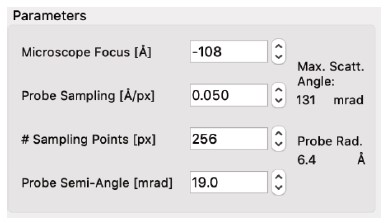
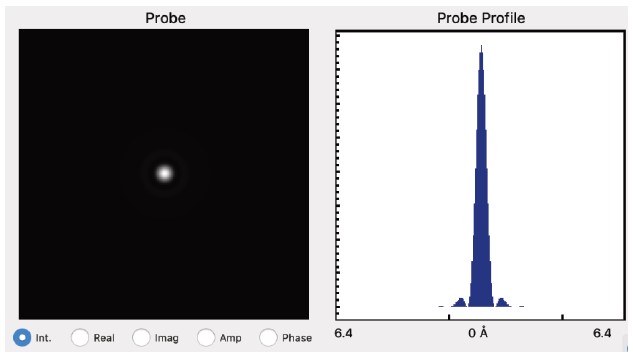
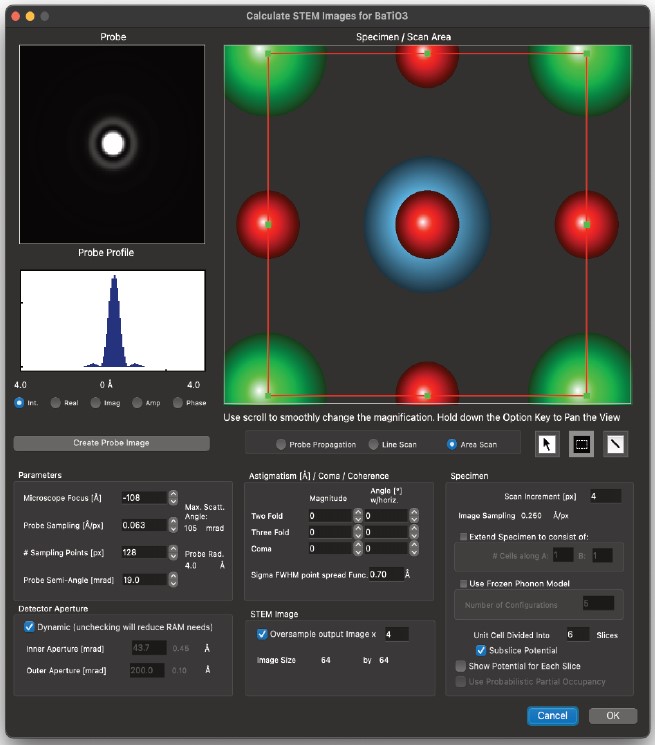
- 顕微鏡のパラメーター(電圧や球面収差など)に基づいて、Tempasは解像度を最適化する焦点位置とプローブ角度を設定します。
ユーザーは当然ながら、実験設定に合った焦点位置とプローブ角度を自由に設定できます。 - 点拡がり関数は、データが拡散し、計算から生じる高周波数「ノイズ」を除去するため、顕微鏡の解像度を制限する経験的値です。これは、各ピクセルの値を応答関数(ガウス関数)と畳み込むことで、ガウス低域通過フィルターとして機能します。
- プローブサンプリングは、計算に含められる最大周波数を設定し、これはミリラジアン単位の最大散乱角によって反映されます。
プローブのサイズは、サンプリングポイントの数とアンストロン単位の実際のサンプリング間隔に依存します。散乱角が検出器の開口部に電子が散乱されるように設定されていることを確認する必要があります。 - 検出器開口部は通常、物理的な設定によって決定され、この設定を反映する必要があります。
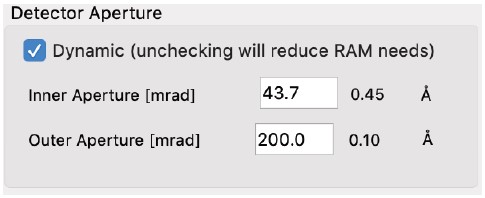
- 「ダイナミック」チェックボックスが選択されている場合、プログラムは以下のウィンドウを出力し、ユーザーは検出器構成(内側と外側の開口部)に応じて画像がどのように変化するかを確認できます。
- チェックボックスがオフの場合、出力は単一のイメージとなり、環状検出器の固定された内側と外側の開口部に基づいて生成されます。

- サンプリングは、計算を高いg値(散乱角)まで拡張できるように十分な精度が必要であるため、顕微鏡が可能な解像度よりも高い解像度を提供します(したがって、以前に導入された点拡がり関数)。したがって、試料は同じ間隔でサンプリングする必要はありません。この場合、試料はポテンシャルのサンプリングの5点ごとにのみサンプリングされます。
- STEM計算は、試料の全体領域または定義された試料の一部に対して実行できます。領域は、ダイアログの試料領域での選択によって指定されます。さらに、計算は線分沿いにも実行可能です。
また、電子ビームが試料を通過する際の広がりを計算するオプションも選択可能です。
- データを滑らかにするため(画像)、計算された画像はオーバーサンプリングされます。画像のオーバーサンプリングと点拡散関数を組み合わせることで、顕微鏡の実際の解像度を反映した解像度で滑らかな画像が得られます。もちろん、サンプリングが粗すぎないように注意する必要があります。
- 出力画像は、計算に使用された単位セルのN×M倍のサイズが与えられます。計算に使用される単位セルは、最も小さな繰り返しセルであるべきです。なぜなら、それより大きい単位セルを使用すると、計算時間が不必要に増加するからです。
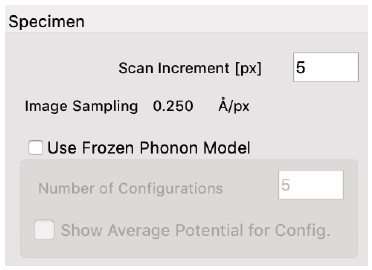
- 右図の設定と、Frozen Phononモデルを使用するオプションが、ポテンシャルの計算方法を決定します。
チェックボックスとその後の値は、単位格子が何スライスに分割されるかを設定します。

- 「Use Frozen Phonon Model」オプションがチェックされている場合、各スライス内のすべての原子は、原子のデバイ・ウォラー因子に対応するシグマを持つガウス分布に従ってランダムに配置されます。
構成の数により、指定された厚さに対してマルチスライス計算が何回実行されるかが決定されます。各計算ごとに、各スライスの原子が移動され、新しい画像が生成されます。最終的に、各構成ごとの画像がすべて加算され、最終画像が生成されます。 - 明らかに、計算時間は構成数の増加に伴い増加します。同様に、各スライスで原子を移動させ新しいポテンシャルを計算する作業はより時間がかかります。標本の各サンプリングポイントに対して、総厚さに対する完全なマルチスライス計算が実行されることを理解する必要があります。
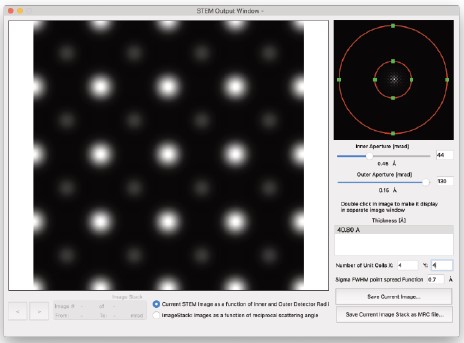
計算が利用可能なCPUコアの数に分散されるため、計算時間はコア数と利用可能なRAMの量に依存します。 - 検出器の開口部の異なる値で計算しデータを保持するための十分なRAMがある場合、出力ウィンドウは次のように表示されます…
4-7. Tablesメニュー
Reciprocal Space Info…
- 現在の構造に関する逆空間データの情報を表示します。
データは逆ベクトルまたは構造因子/消光距離に基づいて並べ替えることができます。
▶間隔と角度計算機…
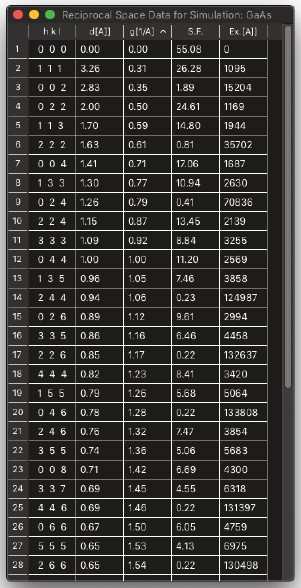
Spacing and Angle Calculator…
- 反射の種類/ファミリーごとの長さおよびd間隔を表示します。2つの反射を表示でき、その反射のセットが存在するゾーンと、それら間の角度がウィンドウの右側に表示されます。
反射は入力可能で、「Calculate?Update Angles」ボタンをクリックすると、反射のファミリー間の角度と、それらが存在するゾーンが右側に表示されます。ベクトルの長さおよび対応する平面間隔は、新しい反射を入力する際にリアルタイムで更新されます。
格子パラメーターは「格子パラメーターを更新」を通じて変更および適用でき、これにより、読み込まれた構造とは異なる構造に対して計算機を使用できます。
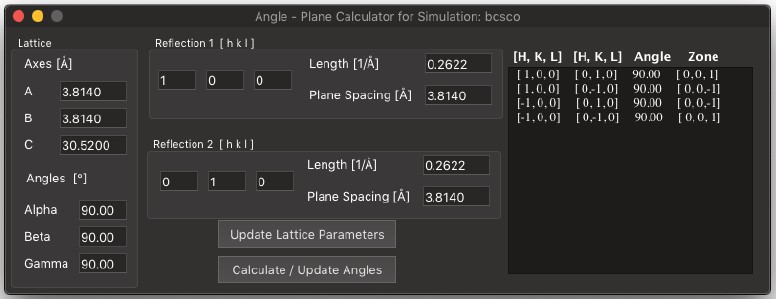
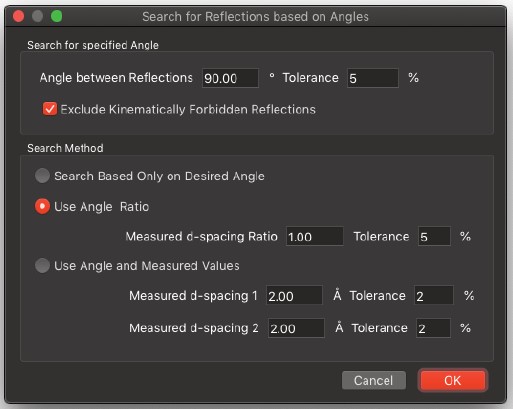
Search for Angle…
- 反射を、ベクトルの長さの比と/または測定された反射間の角度を基にした検索条件を満たすものとして検索できます。
これは、回折パターンのインデックス付けを試みる際に使用できます。比、測定された間隔、および測定された角度に対して、許容誤差を設定できます。
8. Quantitativeメニュー
実験画像と出口波動関数を計算データと定量的に比較するためのメニューです。
構造精製と画像パラメータの精製もこのメニューから実行できます。
◀Quantitative メニュー
ルーティンの実行
- 「Symmetry Transform Calculator」を除くすべてのルーティンは、実験画像として扱われる画像の存在を必要とします。このパッケージの目的は、ユーザーに以下の試行を可能にするツールを提供することです。
- 実験画像と構造モデルからシミュレートされた画像の定量的比較
- 試料の厚さ、対物レンズの焦点ずれ、結晶の傾き、収差など、パラメータの自動調整
- 構造内の選択された原子の原子位置、デバイ・ウォーラー因子、および占有率因子の自動精製
- 実験画像と計算画像との比較は、複数の適合度評価基準を用いて行うことができます。実験画像のサブ領域とシミュレーション画像のサブ領域を比較することも可能です。
定量的な比較方法と構造精製の詳しい情報は、「シミュレーションHRTEM画像と実験との定量的な比較の基礎」の章を参照してください。
| ※ 注意: すべての手順では、実験画像が計算に使用された単位格子の正確な領域をカバーしていることを前提としています。したがって、ユーザーは実験データから単位格子のモチーフを抽出してから使用する必要があります。 単位格子という用語はシミュレーションで使用されるモデルのサイズを指すため、やや曖昧に用いられています。 実験画像はシミュレーションと等しくサンプリングする必要はありません。 ルーチンは実験データをシミュレーションに合わせるように再サンプリングするためです。 パラメータの最適化と構造の最適化には、実験とシミュレーションの適合性を最大化する「唯一の」パラメータ解を探索する複数のアルゴリズムが存在します。 このプラグインは、シミュレートされた熱的アンネリングに基づくアルゴリズムを採用しており、この手法の詳細は本マニュアルの末尾の章で説明されています。この方法の有効性については一切の保証はありません。最終的な解が適合度のパラメーターにおけるグローバル最大値/最小値を表す保証もありません。最適化ルーチンの有効性は初期パラメーターに依存します。初期条件の設定には定まった方法はありませんので、このプログラムの最適化ルーチンを使用する経験を重ねる必要があります。パラメーター/構造の精緻化には、試行錯誤が不可欠な部分です。 |
Load Experimental Image
- 実験用画像の読み込みは、比較に使用する画像を読み込むための起点です。
このコマンドは、使用しているMacOSのバージョンや、Finderユーティリティの他の機能に依存する標準のファイル選択ダイアログを表示します。TIFF、DM3、DM4、MRC、EDM、EBNなど、追加の情報が不要な形式の場合、画像は通常通り読み込まれます。
画像の読み込みに追加の情報が必要な場合、Tempasは画像の読み込みを支援する追加のダイアログを表示します。 - このダイアログでは、異なるデータ形式、バイトオフセット、およびバイトスワップを持つバイナリファイルを読み込むことができます。
- ルーチンがファイルを読み込んだ後、画像は別ウィンドウに表示されます。
Load Standard Deviation Image
- このコマンドは、標準偏差画像を読み込み、平均実験画像と組み合わせてシミュレーション画像との比較に使用するためのものです。
標準偏差画像は、平均画像と組み合わせて、実験データと計算データ間のc-square偏差を計算するために使用されます。
それ以外の場合、入力は平均実験画像の読み込み時とまったく同じように機能します。読み込まれた画像は、別のウィンドウに表示されます。
| ※ 注意: 読み込んだ画像ウィンドウの上に別のウィンドウがある場合、「実験」画像と「標準偏差」画像を前面に表示するために、これらのウィンドウを移動する必要がある場合があります。 これらの画像を自動的に前面に表示するコマンドはありません。 |
Use Front Image as the Experimental Image
- この機能は、アクティブなImageWindowに表示されている画像を比較対象の実験用画像として使用します。
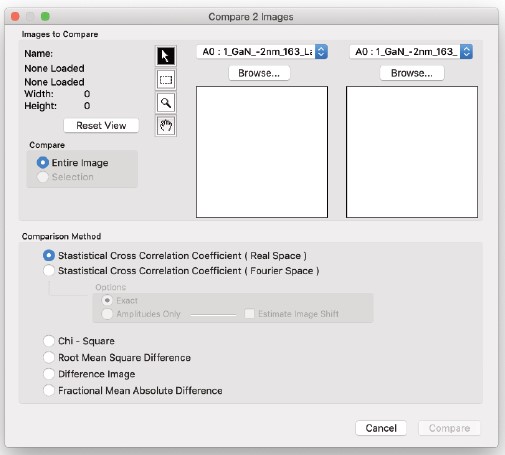
CompareTwo Images…
- 以下のダイアログを表示します。
比較方法などについては、次のセクション「Compare ImageWith Simulation…」で説明しています。
Compare ExperimentWith Simulation
- この操作により、読み込まれた実験画像と標準偏差画像(読み込まれている場合)を表示するダイアログウィンドウが表示されます。実験画像の名前と寸法は、画像の左側に表示されます。
- 画像を比較する際、実験画像は計算された画像のサンプリングに対応するように再サンプリングされます。
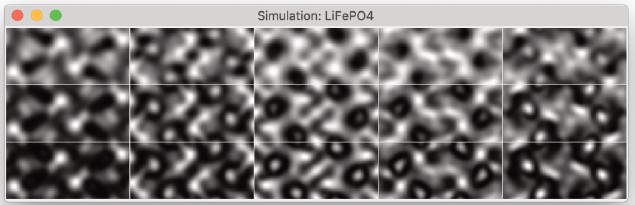
- ここで使用する例は、LiFePO4の[010]面軸方向のシミュレーション画像のセットです。
- 厚さと焦点距離の異なる範囲におけるシミュレーション画像は、以下に示されています。
- シミュレーション画像の中から実験画像として使用し、比較対象とする画像を選択し、[実験とシミュレーションの比較] を実行すると、右図の画面が表示されます。
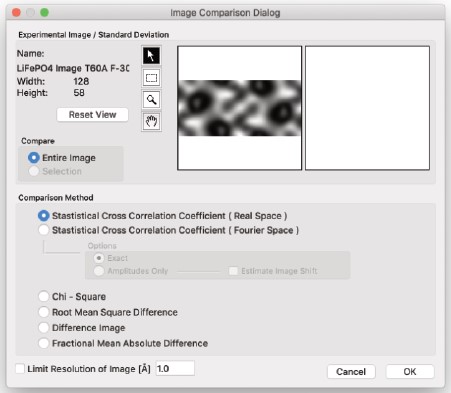
使用できるツール
POINTER TOOL
- 主に、他のツールが主に他のツールがアクティブでないときに使用されます。
SELECTION TOOL
- このツールを使用して、画像内の比較に使用する領域をマークします。画像の外側まで選択しても構いません。選択範囲は実際の画像に合わせてトリミングされます。
HAND TOOL
- このツールを使用して、画像を表示領域内移動させます。
MAGNIFICATION TOOL
- このツールを使用して画像を拡大します。
画像内をクリックする際にOptionキーを押したままにすると、拡大倍率が低下します。
Shiftキーを押したままクリックすると、拡大倍率が2倍ずつ増加または減少します。
Reset View
- ここをクリックして、画像の表示/パン/ズームをリセットします。
比較対象領域の選択
- ユーザーは、画像全体を比較対象として選択するか、画像の一部のみを比較対象として選択するかを選択できます。
- 2つのラジオボタンが用意されています。
Compare Entire Image
- このラジオボタンをクリックすると、選択領域が自動的に画像全体に設定されます。比較領域は赤い長方形として表示されます。
Selection
- ユーザーはまず、選択ツールを使用して画像の領域をマークする必要があります。
ラジオボタンをクリックすると、選択した領域が赤色でマークされ、この領域が画像の比較に使用されます。既に定義された領域を変更するには、新しい領域をマークし、再びラジオボタンをクリックしてください。
注意:選択機能は「差分画像」には適用されません。「差分画像」は自動的に画像全体を比較するためです。
| ※ 注意: 選択機能は「差分画像」には適用されません。「差分画像」は自動的に画像全体を比較するためです。 |
Selecting a method of comparison
- 比較方法または適合度基準は、一連のラジオボタンで選択され、選択項目とその対応する説明および出力は以下に示されます。適合度基準は、比較される各画像に対して計算され、表形式で表示されます。この表は、テキストファイルに保存して後で利用できます。
Statistical cross correlation coefficient (CCC):
- 統計的交差相関係数に関する注記:
交差相関係数は、実験画像と計算画像のパターン間の類似性を測定します。
比較対象の画像は平均レベルを0に設定され、正規化されているため、I(exp) = a * I(calc) + b のようなスケーリングが適用されると、クロス相関係数は1になります。完全一致の場合はCCC = 1、逆コントラストの場合はCCC = -1となります。
Real Space
- これは、実験画像と計算された画像(複数可)間の正規化クロス相関係数の単純な計算です。意味のある結果を得るためには、実験画像の原点が計算された画像の原点と一致する必要があります。
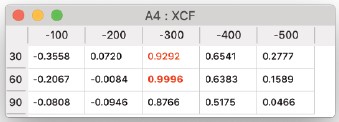
Reciprocal Space
- 逆空間におけるクロス相関の計算には、2つのオプションがあります。
Exact
- 最初のものは、実空間のCCCに相当する正確な計算です。実験画像のフーリエ変換全体はシミュレーション画像のフーリエ変換と比較され、CCCは実空間での計算の逆空間における相当物です。したがって、逆空間のCCCは実空間のCCCと等しくなります。
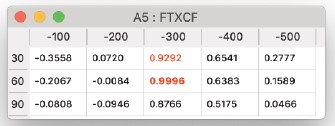
Only Amplitudes
- この計算は、フーリエ振幅のみに基づいてCCCを計算し、(オプションで)プログラムは実験画像と計算画像の間のシフトを推定しようとします。
これは、実験画像の起源が不明な場合に、画像の合わせ合わせや画像の比較に非常に役立ちます。表示される数値は、実験データとシミュレーションを正確な式で比較する前に、実験画像の起源に適用すべきシフトの値です。
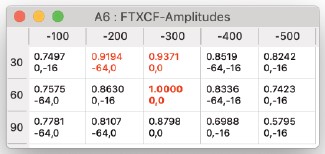
Chi-Square
- この処理は、計算された画像と実験画像の間のカイ二乗偏差を計算します。オプションで標準偏差画像を使用し、平均ピクセル値に関連する不確実性を算出します。
- 標準偏差画像が与えられていない場合、ピクセル値の不確実性はピクセルの強度値の10%に設定されます。カイ二乗適合度基準は画像の平均レベルに敏感であるため、計算された画像を実験前の平均値と同じになるようにスケール調整し、カイ二乗を計算します。
低い値はより良い適合を示し、値が1の場合、実験とシミュレーションが実験値の不確実性範囲内で一致していることを意味します。
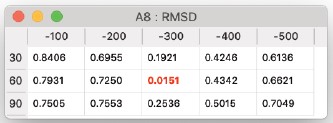
Root Mean Square Difference
- これは、実験とシミュレーションの間の平均二乗誤差を計算します。
値が低いほど、実験とシミュレーションの適合性が良好であることを示し、0は実験とシミュレーションの完全な一致を意味します。値は比較される画像の平均レベルに依存するため、シミュレーションは実験と同じ平均を持つようにスケール調整されています。右図の表は、RMSD比較の結果を示しています。
Difference Image
- このケースでは2つの計算が行われます。1つは差分画像(複数可)を生成し、これらは擬似カラー化されます。
具体的には、実験とシミュレーションが1標準偏差以内に一致する場合、ピクセルは黒で表示され、1.5標準偏差未満の場合、ピクセルは緑で表示され、それ以外のピクセルは赤または青の濃淡で表示されます。これは、シミュレーションの値が実験の値よりも低い場合か高い場合かによって異なります。

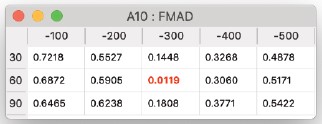
Fractional Mean Absolute Difference
- この式は、実験データとシミュレーションデータ間の分数平均絶対差を計算します。
CompareXWAmplitude/Phase with simulation
- 画像の場合と同様に機能しますが、実験データは出口の波動関数(振幅または位相)と比較されます。
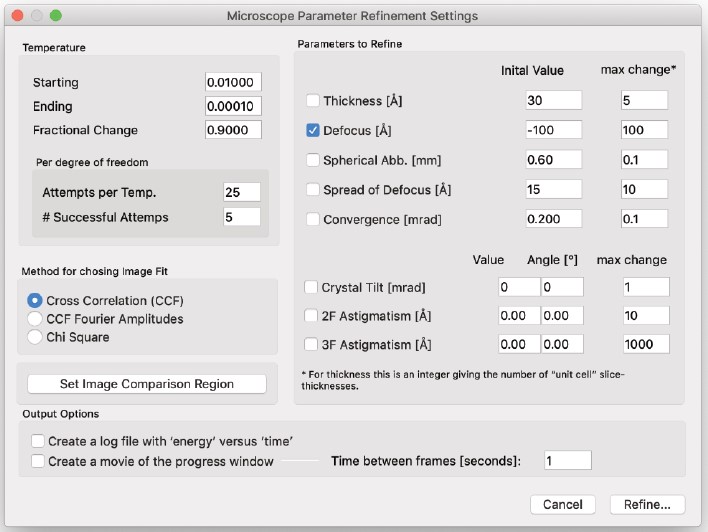
Refine Parameters
- パラメーターを最適化… シミュレーション画像を生成するパラメーターを実験と理論の間の「最良」の適合を与えるように探す試みを行います。この検索ルーチンは「シミュレート熱的焼鈍」の概念に基づいており、パラメーターの初期設定、初期温度、終了温度、パラメーターの最大変化量、およびシステムの「エネルギー」を測定する適合度基準が必要です。
シミュレート熱的アンネリングの詳細な説明は、このマニュアルの最終章を参照してください。 - コマンドを実行すると、アルゴリズムに入力パラメーターを指定するための以下のダイアログが表示されます。
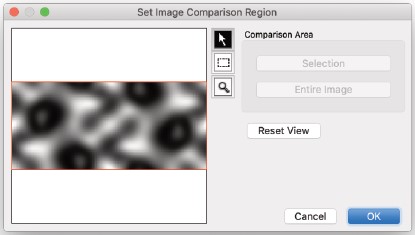
Setting Image Comparison region
- 比較に使用する領域は、「画像比較領域を設定」ボタンを使用して設定されます。
画像領域の選択は、前節で説明した画像比較時の手順と同様に行います。
Running the parameter refinement
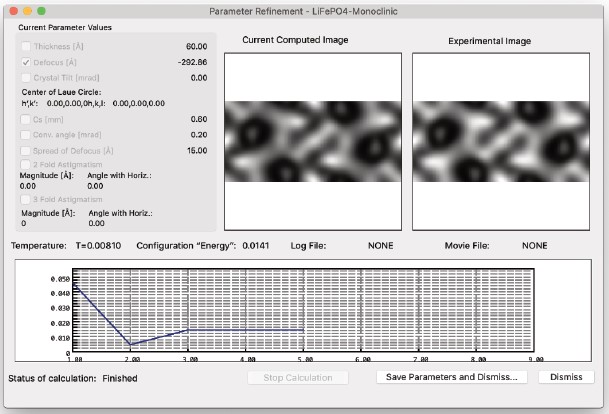
- 領域を選択した後(画像全体を比較する場合、デフォルト設定のため不要)、調整するパラメーターを選択し、OKをクリックすると、パラメーター調整の進行状況ウィンドウが表示されます。調整が満足のいくように進んでいない場合、Apple-Commandキーとピリオドキーを同時に押すことで計算をキャンセルできます。オプションでログファイルを書き出し、時間/温度に対する「エネルギー」のグラフを作成したり、ムービーを生成して再生したりできます。出力時のフレーム数/秒を設定可能です。
- 実行終了時、ダイアログボックスを単に閉じると、最終的なパラメーターの設定は破棄されます。または、パラメーターを新しい構造/シミュレーションファイルとして保存することもできます。
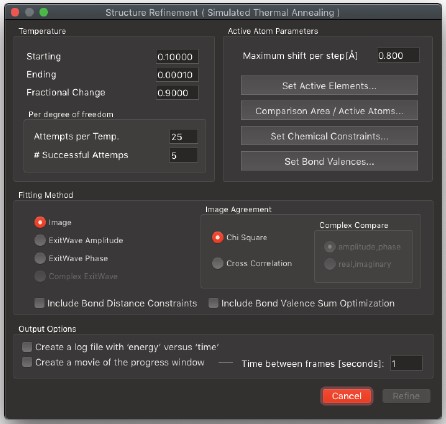
Refine Structure
- 構造精製はパラメーター精製と同じように機能します。ただし、この場合、変更されるのは構造そのもので、特に選択された原子の座標やデバイ・ウォラー因子、占有率などが対象となります。コマンドを実行すると、以下のダイアログボックスが表示されます。
構造精緻化には、アクティブな元素や変更する座標など、いくつかのオプションが関連しています。シミュレートされた熱的焼成の標準パラメーターを指定する必要があり、適合度パラメーターも指定する必要があります。
ログファイルやムービーなどの出力オプションは、パラメーター精緻化の場合と同一です。さらに、「構成エネルギー」の計算に、選択された結合距離と選択された結合価数和に依存する項を含めることが可能です。
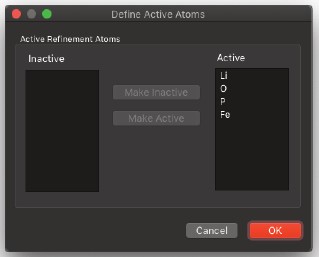
- アクティブ要素を設定する
以下のダイアログが表示されます。デフォルトでは、すべての要素がアクティブになっています。アクティブな要素を選択し、「非アクティブにする」ボタンをクリックすると、選択した要素が非アクティブリストに移動します。
アクティブ要素にリストされているからといって、その要素のタイプが精製手順で使用されるわけではありません。シミュレートされた熱的焼成を実施する前に、比較に使用する領域と最適化対象の原子を指定する必要があります。
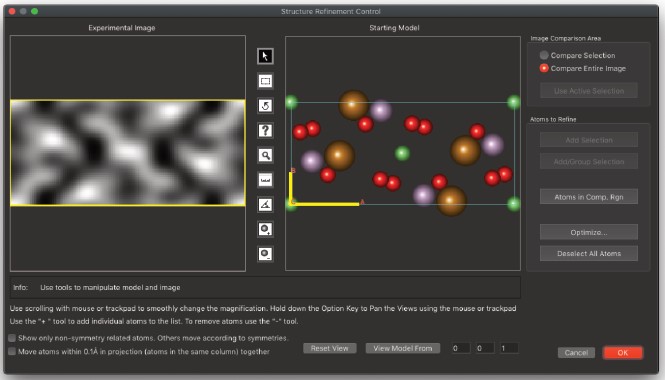
- 比較対象領域を設定し、アクティブな原子を選択する
画像比較領域を設定するため(以前に説明したとおり)および精製対象の原子を選択するために使用されます。右図のウィンドウが表示されます。- 比較に使用する領域
- 選択
比較領域を選択矩形に設定します。 - 全体画像
比較領域を全体画像に設定します。 - 精製対象原子
- 選択を追加
モデルウィンドウで設定された選択矩形内含まれる原子を原子リストに追加します。 - 選択の追加/グループ化
原子を精製リストに追加しますが、このリスト内のすべての原子を単位として移動するように制約します。
Atoms In Comparison Region
- 画像の比較用に設定された矩形内に存在する原子を含めるように、精製リストを設定します。
Optimize…
- 選択された原子(精製リスト内のもの)のどのプロパティが変更されるかを指定します。右図のウィンドウが表示されます。
- 通常、z座標を変更しても効果はありません。なぜなら、画像シミュレーション手順では、単位格子内の原子の2次元投影を使用しているためです。ただし、対称性演算子を使用する場合、z位置を変更すると、対称性に関連する原子のxとyにも変化が生じる可能性があります。
- 原子(またはグループ)を変更するたびに、その原子/グループ用の新しいパラメーターセットが作成され、テストされます。「各変数を個別にテスト」がチェックされている場合、各試行では1つのパラメーターのみが変更されます。したがって、xとyが上記でチェックされている場合、原子に対してxとyは同時に変更されます。ただし、「各変数を個別にテスト」がチェックされている場合、1回目はxが変更され、別の回ではyが変更されます。
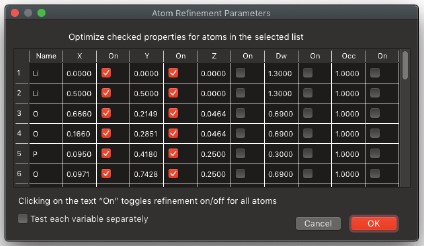
Deselect All Atoms
- 最適化対象の原子セットを定義し直すことができます。
Show only symmetry related atoms/Use Symmetry elements
- 構造が基底原子セットと対称性演算子セットで定義される完全な結晶である場合、基底原子の位置を精緻化し、対称性に関連する原子を結晶の空間群を保持するように移動させることができます。
このオプションを選択すると、モデルに表示されるのは基底原子のみとなります。したがって、精緻化対象の原子はその基底から選択され、基底の変更は構造全体に反映されます。
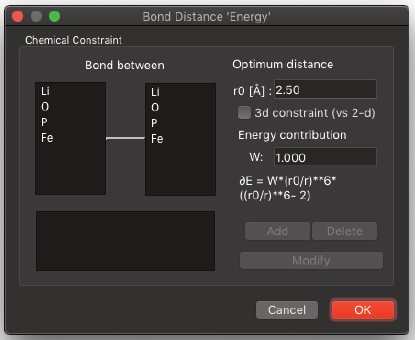
Set Chemical Constraints
- 右図のウィンドウを表示します。
- 結合距離に依存する項を含む構成エネルギーを指定するために使用できます。2つの原子間の最適な結合距離を指定することができ、それが2次元または3次元の制約であるかどうかにかかわらず、エネルギー計算における項の重みを指定することも可能です。
結合距離が定義されていても、結合距離エネルギー項の包含は、メインの「構造精製」ウィンドウからオン/オフを切り替えることができます。
Include Bond Valence Sum Optimization
- この機能により、結合価数和を用いて配置のエネルギーを測定することが可能になります。
この機能は、以下のウィンドウを表示し、そこでアクティブな結合を指定し、結合価数和を計算するための原子間の最大距離、原子対の最初の原子の価数、および結合定数を設定します。各「結合」には独自の重みが設定され、結合価数エネルギー項全体には全体的な重みが設定されます。
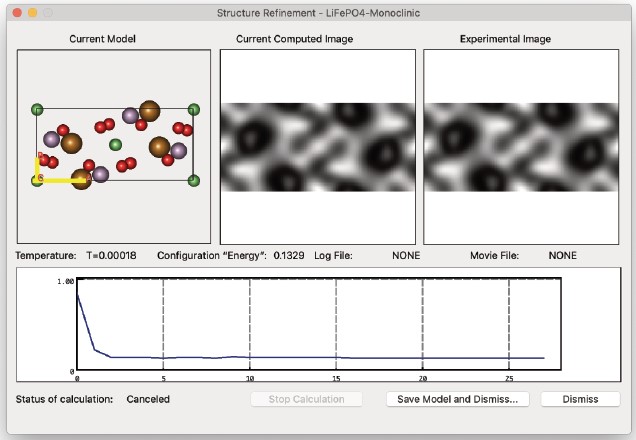
Running the Refinement
- パラメーターを設定し「OK」をクリックすると、進行状況ウィンドウが表示されます。
- 現在の原子配置と対応するシミュレーションエネルギーが表示されます。エネルギーは「時間/温度」の関数として独自のウィンドウに表示され、システムが望ましい方向に移動していることを確認するために監視できます。重要な点は、システムが構成エネルギーの有意な最小値を見つけるための特定のレシピは存在しないということです。最適化の成功は、初期構成が「解」からどの程度離れているか、およびアンネリングパラメータの選択に依存します。
これは、単に実行すれば正しい答えが得られるような、単純なブラックボックスアプローチではありません。システムの理解、適切な初期構造を選択する感覚、および「アンネリングパラメーター」を選択する経験は、結果の最終配置に自信を持つために不可欠です。異なる入力パラメーターを試すことが推奨されます。 - シミュレーションパラメーターの最適化と同様に、アンネリングプロセスのログファイルを保存したり、ムービーを作成したりすることが可能です。ムービーの保存は、精製に数時間/日かかる場合、システムが時間経過でどのように変化したかを確認するために非常に有用です。ムービーファイルは急速にサイズが増加するため、数時間分の期間をカバーする場合、フレーム/秒の数を適切に選択することが重要です。
- 実行終了時、最終構造は破棄するか、後で使用するために構造ファイルとして保存できます。また、通常の手順で「Command + Period」キーの組み合わせを使用して実行を中止することもできます。
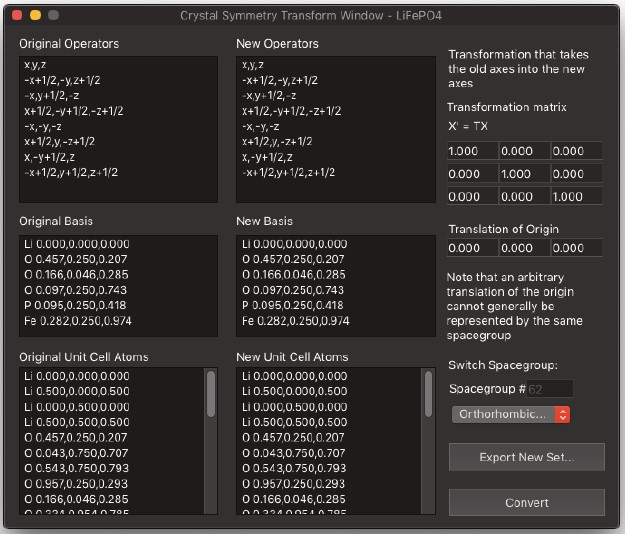
SymmetryTransformCalculator
- 「対称変換計算機」を選択すると、モーダルダイアログウィンドウが表示され、単位格子の軸と原点の変更に伴い、ユーザーが別の対称演算子と基底原子の位置を見つけるのに役立ちます。
入力は、使用中の空間群から得られる元の対称性演算子と元の基底原子です。新しい単位格子軸 a’、b’、c’ は、変換行列 T によって与えられ、古い単位格子系で指定された原点の移動(分数座標)と組み合わせて定義されます。コマンドを実行すると、以下のウィンドウが表示されます。
リスト
Original Operators
- このリストは、現在の空間群の対称操作を示します。
最初は使用中の結晶の対称操作ですが、空間群は「Switch Spacegroup」コマンドで変更できます。
Original Basis
- 基底原子は、現在の結晶の原子のことです。
Original Unit Cell Atoms
- このリストは、元の基底原子に対して使用されている空間群の対称性演算子の作用によって生成される原子を示しています。
New Operators
- これらの演算子は、座標系の変換操作と原点を元の空間群の生成点へ移動する変換を組み合わせた結果として得られるものです。
New Basis
- これが変換後の基底です。
Original Unit Cell Atoms
- このリストは、新しい空間群の新しい対称演算子の作用によって生成される原子を示しています。
この空間群は、新しい基底原子セットに適用されています。
Convert
- このボタンをクリックすると、変換された対称演算子の集合、変換された基底、および新しい原子位置の計算が開始されます。
| ※ 注意: 任意の入力が対称性を生じないことを理解することが重要です。それでも、対称性演算子の変更により、同じ空間群で表現される可能性があります。 |
Export New Set
- ユーザーが新しい基底と対称性演算子を新しい構造ファイルとしてエクスポートできるようにします。
9. Processメニュー
プロセスメニューは最も大きなメニューであり、すべての画像処理機能の源です。
このメニューにはサブメニューも含まれています。
Image Calculator
- HPスタイルの計算機(HP式計算機)を使用した数学的表記を画像と数値に適用する。
- FFT
2次元画像に対してフーリエ変換を実行します。多くの実装とは異なり、画像の次元が2の冪乗である必要はありません。ただし、画像は正方形である必要があります。
スクリプトからフーリエ変換を実行する場合や、Image Calculatorを通じて呼び出した場合、画像は正方形である必要はありません。この場合、フーリエ変換画像はu方向とv方向でサンプリングが不均一な状態で表示されます。
Linked FourierTransform
- フーリエ変換は、画像に選択範囲が存在するか否かによって、2つの異なる方法で機能します。
- 選択範囲が存在する場合…
選択範囲のフーリエ変換を、元の画像と共に独立したウィンドウに表示します。
選択範囲を画像内で移動させると、フーリエ変換は選択範囲の変換結果を更新して表示します。 - 選択範囲なし…
元の画像のフーリエ変換を新しいウィンドウに表示します。フーリエ変換に適用されたマスクは、元の画像に「即時的に」反映されます。マスクが変更されると、画像が更新されます。
Hanning Masked FFT
- 2次元画像に対してフーリエ変換を実行します。画像はまず、円形の2次元ハンニングマスクでマスクされます。
Soft Circular Masked FFT
- 2次元画像に対してフーリエ変換を実行します。画像はまず、円形の2次元マスクでマスクされます。
Inverse FFT
- 2次元画像に対して逆フーリエ変換を実行します。多くの実装とは異なり、画像は2の冪乗の次元である必要はありません。ただし、画像は正方形である必要があります。
Power Spectrum
- 実数四角形画像のパワースペクトルを計算します。
Edit Mask…
- 指定されたタイプのマスクに関連する特定の設定を許可します。格子マスクのプロパティの例は以下に示します。
Lattice Mask Properties..
Annular Mask Properties…
Apply Mask(s)
- 定義されたマスクを画像に適用します。
Fourier Filters
- 以下のフィルターを含みます。
Wiener Filters – different strengths
- ウィーナーフィルターは、ノイズのパワースペクトルを推定し、その推定値と信号の推定値に基づいて最適なフィルターを生成する自動フィルターです。
Background Subtraction Filters – different strengths
- ウィーナーフィルターと同様に、このフィルターはノイズのモデルを使用して、画像から不要な情報を「除去」します。
結晶構造からの情報はブラッグ反射でピークを示すため、非晶質基板からのノイズスペクトルを、ノイズが周波数にのみ依存し、方向には依存しないという基準に基づいて推定できます。したがって、ノイズスペクトルは回転対称であり、結晶部分からの情報とは異なります。
Gaussian Low Pass Filter…
GaussianHigh Pass Filter…
- ガウスマスクフィルターを使用して、画像の高周波成分の一部を除去(低域通過)または低周波成分の一部を除去(高域通過)します。
Annular Low Pass Filter
AnnularHigh Pass Filter
- 環状マスクを使用して、スペクトルの高周波数または低周波数成分を排除します。
Spatial Filters
- 右図のフィルターを含みます

Convolution…
- カーネルを定義するための以下のダイアログを表示します。事前定義されたカーネルは利便性のために用意されていますが、係数を自由に変更できます。
Sharpen
- 3×3のカーネルにすべての要素に-1を適用し、中央の要素のみに9の値を適用することで、画像をシャープにします。
Smooth
- 画像内の各ピクセルを、その周辺のピクセルの平均値で置き換えます。中央のピクセルの重みは2、周辺のピクセルの重みはそれぞれ1です。
Laplacian
- ラプラシアンは、シャープニング操作と同様に3×3のカーネルを使用しますが、中央のピクセルの重みが9ではなく8となっています。
Sobel
- 2つの独立したカーネルを使用し、それぞれx次元とy次元に対応しています。
- カーネルの値は
| -1 0 1 | -1 -2 -1 | ||
| X: | -2 0 2 | Y: | 0 0 0 |
| -1 0 1 | 1 2 1 |
Remove CCD Defects
- この処理は、画像内のピクセル値が期待される範囲外にあるかどうかを確認します。範囲外と判定されたピクセルは、CCDカメラのピクセル欠陥として扱われ、そのピクセルの周囲のピクセル値が期待される範囲内にある場合の平均値で「修復」されます。
Transform
- 以下の操作を含みます
Invert
- 画像を反転させます。0を基準に反転します。
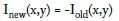
Scale…
- 現在の画像をスケーリングします。新しい画像は、xとyの相対的なサンプリングを保持するかどうかは場合によります。
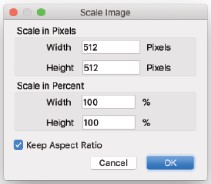
Rotate…
- 現在の画像を回転させる
Oversample
- 画像のオーバーサンプリングを特定の倍率で行う。画像のオーバーサンプリングを行う際、周波数スペクトルはゼロで拡張され、その後フーリエ変換により実空間に戻される。
Repeat…
- 現在の画像をn行×m列に繰り返し表示します。この操作は、元の画像がx方向とy方向で周期的な場合、より意味を成します。
Pad…
- 現在の画像を新しい寸法に拡大します。
Bin Image
- 指定された倍率で画像を縮小します。
Flip about Vertical Axis
- メニュー項目に書かれているように…
Flip AboutHorizontal Axis
- メニュー項目に書かれているように…
Rotate 90 Deg. Clockwise
- メニュー項目に書かれているように…
Rotate 90 Deg. Counter Clockwise
- メニュー項目に書かれているように…
Statistics
- 右図の操作を含みます。
データは情報ウィンドウに表示されます。

Calibrate…
- 定規ツールで長さがマークされると、画像はキャリブレーションできます。線が描かれていない場合、メニューコマンドは非活性です。画像は「オブジェクトの編集…」メニューコマンドを通じてキャリブレーションすることもできます。その場合、線を描く必要はありません。
Extract From Complex
- 前面の形状が複雑な場合、複雑な形状のさまざま要素から画像を作成することができます。

Correlation / Convolution
- 右図の操作を含みます

Auto Correlation
- 単一の画像に対して処理を行い、その画像の自己相関関数を計算します。
Cross Correlation…
- 2つの画像のクロス相関画像計算します。
Phase Correlation…
- 2つの画像の位相に基づいて相関関数を計算します。
フーリエ成分の振幅は無視されます。
Convolute…
- 2つの画像から畳み込み画像を生成します。
Deconvolute…
- 3つ目の画像を生成します。これは、最初の画像と2つ目の画像でデコンボリューション処理されたものです。
Align…
- 2つの画像を、クロス相関画像または位相相関画像のいずれかを使用して一致させようとします。
Azimuthal Average
- 以下に示された操作を含みます。
右図の画像を起点として、各種操作の結果は以下に示されています。

1D Image
- 方位平均を計算し、1次元トレースとして表示します。
2D Image Split Plane
- 画像の元の左半分を表示し、右半分を2次元方位平均で置き換えます。
2D Image
- 方位平均から2次元画像を作成します。
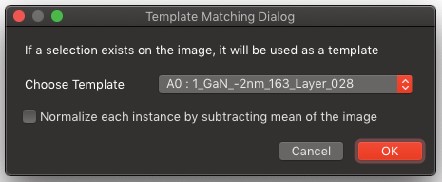
Template Matching…
- テンプレートの画像内の位置に応じて、テンプレートのクロス相関係数を含む画像を計算します。クロス相関係数は、元の画像内の各ピクセル位置に対して計算されます。
- 例として、テンプレートマッチング操作をゼオライトの結晶構造を含む画像に適用します。この結晶構造は電子線によって迅速に破壊されます。テンプレートとして使用される領域は選択範囲で示されています。この操作は、画像内のテンプレートに類似する領域を特定しようと試みます。
- メニューバーから「テンプレートマッチング」を選択すると、右図のダイアログが表示されます。
- その結果、テンプレートと元の画像の基盤領域との間のクロス相関係数を各テンプレートの位置ごとに示す新しい画像が生成されます。
- クロス相関画像のピークは、テンプレートと基盤画像との間のクロス相関係数が指定された閾値を超える位置に対応しています。
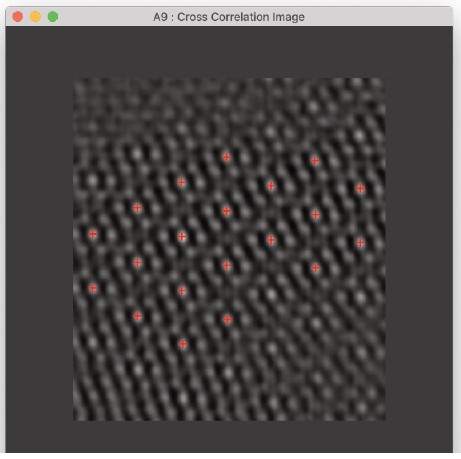


- 上記で発見されたピークを用いて、各ピーク位置における画像を合計することで得られる平均テンプレート画像を計算できます。出力は、上記右図の平均テンプレートを生成します。
Peak/Lattice Analysis
- 右図の操作を含みます
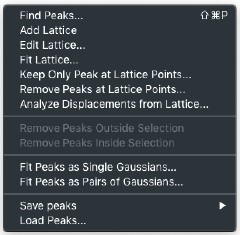
Find Peaks…
- 次のダイアログで指定された条件を満たす画像内のすべてのピークを検索します。
- ピークは画像上にマークされます。基準を変更してピークを再検索すると、新しいピークセットがマークされ、古いピークが置き換えられます。ピークは、オブジェクト全体を選択して削除することができます。また、ピークはコピーして別の画像(できれば同じサイズ)に貼り付けることもできます。ピークのリストは、ピーク位置のセットを通じて調整可能な関連格子と組み合わせて、変位解析に使用できます。
- 画像上に選択範囲がある場合は、選択範囲内にあるピークのみが検索されます。最初に画像全体からピークを検索し、選択範囲を作成してから、選択範囲の内側または外側のピークを保持するように選択することもできます。


Add Lattice
- 画像上に格子を配置します。格子にはハンドルがあり、格子の原点と軸を移動できます。
- 格子ベクトルによって定義される格子間隔の数を変更します。
- 格子ベクトルの終点をOptionキーを押しながらクリックすると、格子間隔の数がクリックごとに1ずつ増加します。OptionキーとShiftキーを同時に押すと、間隔の数が1ずつ減少します。
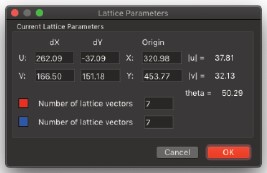
Edit Lattice..
- 方ラティスのパラメータを編集できます。
これにより、ラティスのすべてのパラメータを数値で設定できるようになります。位平均から2次元画像を作成します。
Fit Lattice..
- ラティスが定義されている画像に関連付けられたピークのリストを用いて、最小二乗法に基づくラティスの微調整を行います。
- ラティスは、ラティスツールまたはメニューコマンド「ラティスを追加」を使用して作成する必要があります。ラティスの原点は、ピークの「中心」にあるピーク上またはその近くに配置する必要があります。ラティスは移動可能であり、ラティスベクトルは調整可能です。微調整後はラティスを移動しないでください。ラティスはオブジェクトであるため、コピーして別の画像に貼り付けることができます。
- 画像内に選択矩形が存在する場合、選択矩形内のピークのみがラティスの微調整に使用されます。
Analyze Displacements…
- 変位解析を可能にします。変位は、通常、精密化された格子から得られる参照格子に対する相対的なものです。
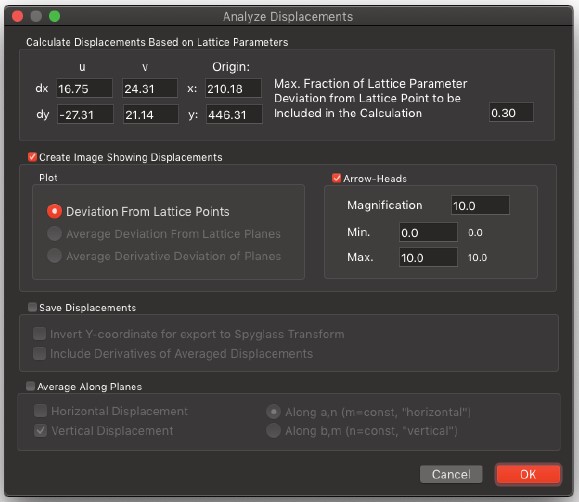
Geometric Phase Analysis…
- 空間周波数の変化から変位解析が可能になります。
幾何学的位相計算については、第11章で詳しく説明します。
Cryst Image Processing…(Crystallographic Image Processing…)
- 正方形または正方形の選択範囲を持つ実空間画像に対して呼び出すことができます。
- 結晶学的画像処理は、結晶材料の画像のフーリエ変換が、2次元投影の対称性が可能な平面群のいずれかに属するために、フーリエ係数間に特定の関係を示すという事実に基づいています。この関係は、「単位格子モチーフ」を使用して空間を完全に満たすために必要なものです。
- したがって、結晶材料の像をフーリエ変換することで、フーリエ係数が様々な面群の対称性を満たすのにどの程度近いかを計算できます。例えば、4回対称の面群P4は、4つのフーリエ係数の振幅が同じで、位相がすべて同じ(0°または180°)になるように連結されている必要があります。
それぞれの可能性のある面群について、実験像のフーリエ係数と面群対称のフーリエ係数の位相差を調べることができます。結晶のモチーフが特定の面群の対称性を持つと推定された場合、振幅と位相の対称性を実験係数に適用し、逆フーリエ変換を実行して、結晶の対称化されたモチーフに面群対称性を課すことができます。
もちろん、これによりモチーフは完全に対称化され、画像に存在していた可能性のある他の情報は表示されなくなります。 - アクティブウィンドウに結晶物質を含む領域の正方形画像が表示されているときにメニューコマンドを選択すると、次のウィンドウが表示されます。
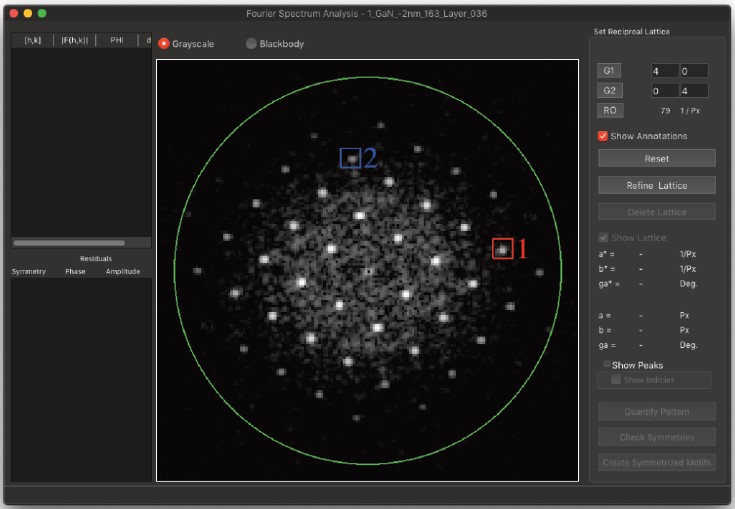
- まず、ハニングマスクフーリエ変換を計算します。フーリエ変換が計算されたら、aツールとbツールを使用し、逆格子空間を定義する2つの連続した反射をクリックして逆格子空間格子を設定する必要があります。格子の精密化と情報抽出に使用される反射の数は、円形絞りツールによって制限できます。
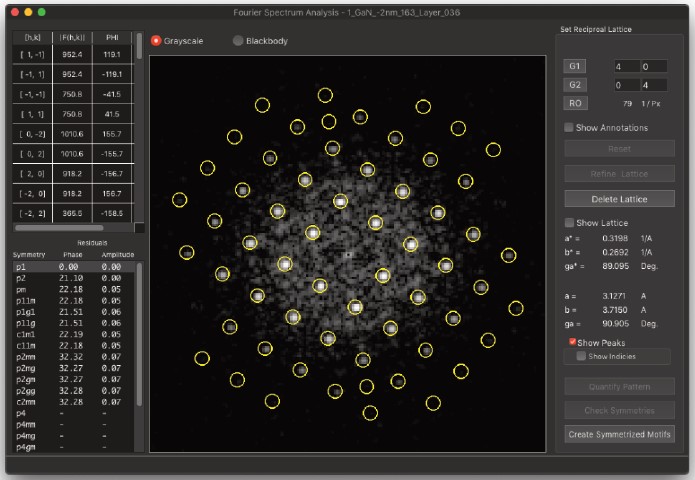
- 格子反射をマークしたら、次に「格子を精緻化」コマンドを実行します。これにより格子がマークされ、結晶を定義するすべての反射が精緻化されます。もし精緻化されない場合は、最初からやり直すことができます。
- 格子の精緻化が完了したら、「パターンを定量化」をクリックします。これにより、格子点におけるフーリエ変換からすべての位相と振幅が抽出され、格子ピークに位置する反射の抽出されたすべての振幅と位相が表示されます。
- 「対称性をチェック」を実行することで、対称性の有無をテストできます。
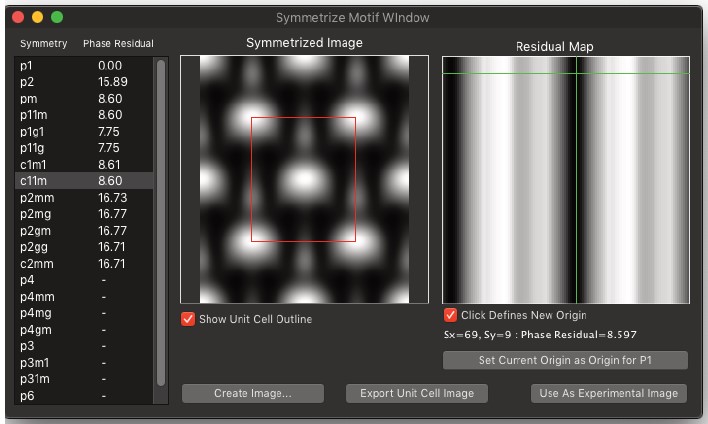
- それぞれの対称性をテストし、反射に適用することで、新しい単位格子モチーフを作成できます。単位格子モチーフの原点は右側に表示され、変更可能です。解を選択すると、適用された対称性を持つ新しい画像が作成され、シミュレーションと比較するための画像としても使用できます。
Focus Determination
- 右図の操作が含まれます。
- HRTEM像からのフォーカス検出については、第12章で詳しく説明します。

Image Info…
- 画像に関する一般的な情報を右図に示すように表示します。
5. Contextual メニュー
多くのオブジェクトにはコンテキストメニューが関連付けられています。以下に、そのいくつかと、関連付けられているオブジェクトを示します。
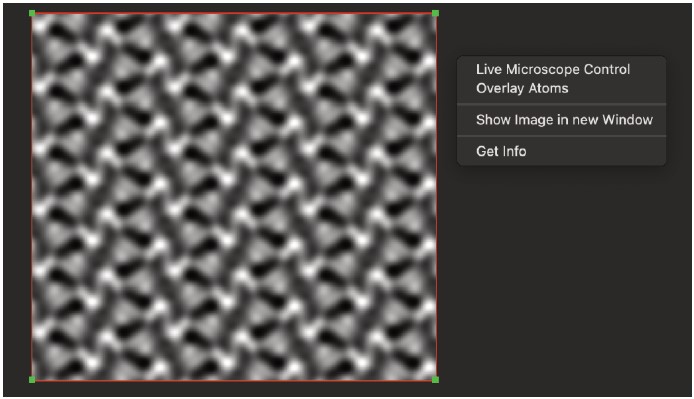
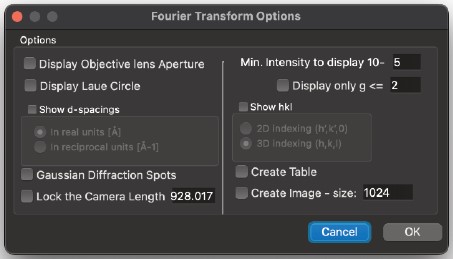
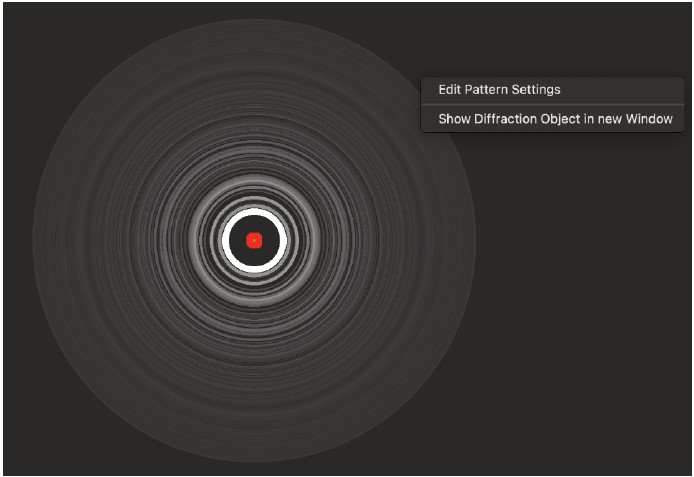
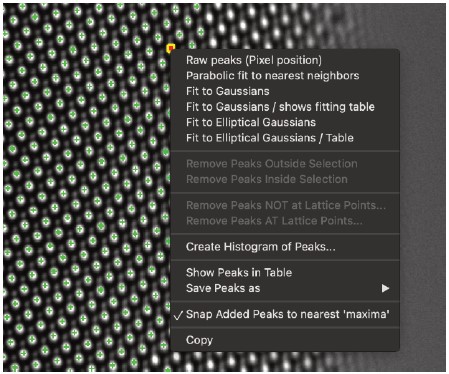
6. ファイル形式
ファイルメニューの「新規…」で作成される構造ファイルは、テキスト形式のファイルで、テキストエディタで作成できます。Tempas を使ってこのファイルを作成するのではなく、ファイルを直接編集することが望ましい場合もあります。実際、ユーザーは構造ファイル内のデータを生成するプログラムを作成したい場合もあります。特にそのような目的のために、構造ファイル .at のフォーマットは以下のとおりです。
| Line | Parameter(s) | Meaning |
|---|---|---|
| 1 | Title | この構造の任意の説明 |
| 2 | SpaceGroupNumber | 名前の通り、230 個の空間群 (1-230) の 1 つ |
| 3 | a b c a b g | 格子定数と角度 |
| 4 | Gmax | マルチスライス計算における逆格子ベクトルの最大値 ポテンシャルはこの値の 2 倍まで評価されます (単位 Å-1) |
| 5 | iu iv iw | 電子ビームの方向(実空間結晶格子ベクトル単位) |
| 6 | NSymops Nslices | 対称演算子の数、(I3d) 単位セルあたりのスライス数、およびNslicesが1と異なる場合のみ、2次元(0)または3次元(1)ポテンシャル計算を示すフラグ |
| 7 | NBasis Ntypes | 基底に含まれる原子の数、異なる原子タイプの数 異なるタイプには、異なる化学記号または異なるデバイ・ワラー係数が関連付けられます |
| 8 | it symb x y z | 原子タイプ(1 – NTypes の数)、化学記号、格子ベクトルの相対単位での x, y, z 座標、デバイ・ワラー係数、占有係数 |
| 9 | 原子番号2については8行目と同じ | |
| 10 | 原子番号3については8行目と同じ | |
| 8+NBasis | MicName Cs Del Th | 顕微鏡の名前、球面収差(mm)、焦点ずれの広がり(Å)、および発散半角(mrad) |
| 9+NBasis | Voltage | 加速電圧(kV) |
| 10+NBasis | Lh Lk | ラウエ円の中心を、変換された逆格子のhとkの単位で表したもの(実数) |
| 11+NBasis | Thickness | 試料の厚さ、またはT1,T2,DT 最初の厚さ、最後の厚さ、増分 カンマは必須 |
| 12+NBasis | IPlot | プロット可能な振幅(YES/NO) |
| 13+NBasis | ih ik il | 保存する反射のインデックス |
| Defocus | 対物レンズのデフォーカス( IPlot == NO の場合 ) | |
| D1,D2,DD | 最初のデフォーカス、最後のデフォーカス、増分 カンマは必須( IPlot == NO の場合 ) | |
| 14+NBasis+NAmp | ApertureRad | 対物レンズのアパーチャー半径(Å-1 単位) |
| 15+NBasis+NAmp | Ah Ak | 対物レンズの絞りの中心を、変換された逆格子単位胞のh、kの単位で表したもの。 |
| 16+NBasis+Namp | Oh Ok | 光軸の中心をAh、Akと同じ単位で表します。 |
| 17+NBasis+Namp | s1,s2,s3 | 対称演算子番号1。例:x+1/3、y+5/6、z+1/3。カンマは必須 |
| 17+NBasis +Namp+NSymop | istat | この構造の計算ステータス、新しい構造の場合、これは1になります |
| 18+NBasis +Namp+NSymop | Vibration | A における機械振動の半値幅 |
| ※ 注意: Microsoft Word、Write Nowなど、異なるワープロソフトを使用する場合は、テキストファイルが最後に「テキスト」形式で保存されていることを確認してください。 |
7. 計算例
Tempasを用いた計算例として、BCSCO超伝導体構造を考えます。Tarasconら (1988) によって決定された構造を用いて、モデル構造の入力、構造の検証、回折パターンとシミュレーション画像の計算、そして表示と印刷に必要な手順を示します。
TarasconらがPhys. Rev. B 37 (1988) p.9382-9389に発表したように、この正方晶構造は以下のパラメータを持ちます。
空間群:I4/mmm
格子パラメータ:a=b=3.814Å、c=30.52Å、a=b=g=90
基底関数には9つの原子位置があります。
| Atom | Wyckoff notation | x | x | z | Occupancy |
|---|---|---|---|---|---|
| Ca | 2a | 0 | 0 | 0 | 1 |
| Sr | 4e | 0 | 0 | 0.1097 | 1 |
| Bi | 4e | 0 | 0 | 0.3022 | 0.87 |
| Bi | 4e | 0 | 0 | 0.2681 | 0.13 |
| Cu | 4e | 0 | 0 | 0.4456 | 1 |
| O(1) | 8g | 0.5 | 0 | 0.446 | 1 |
| O(2) | 4e | 0 | 0 | 0.375 | 1 |
| O(3) | 4e | 0 | 0 | 0.205 | 1 |
| O(4) | 4e | 0.5 | 0 | 0.205 | 0.065 |
すべての原子の等方性熱パラメータは 3.6 Å2 に固定されています。
Tempas に新しい構造を入力するには、まず「ファイル」メニュー(セクション 3.3)から「新規構造ファイル…」を選択します。「新規ファイル」ダイアログにファイル名を入力すると、Tempas はデフォルトの立方構造を作成します。
入力データを保存するファイル名を指定します。後で開くときに簡単に覚えられるような、わかりやすい名前にしてください。拡張子は使用しないでください。
構造に合わせてデータを変更する必要があります。シミュレーションを素早く設定する最も簡単な方法は、メニューバーの「パラメータ」メニューの「すべてのシミュレーションパラメータを表示…」メニューコマンドを選択することです。
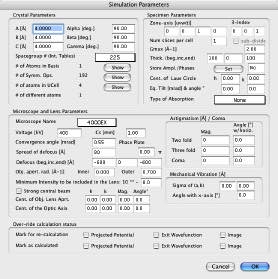
これにより、計算のすべてのパラメータを設定できる次のダイアログが表示されます。
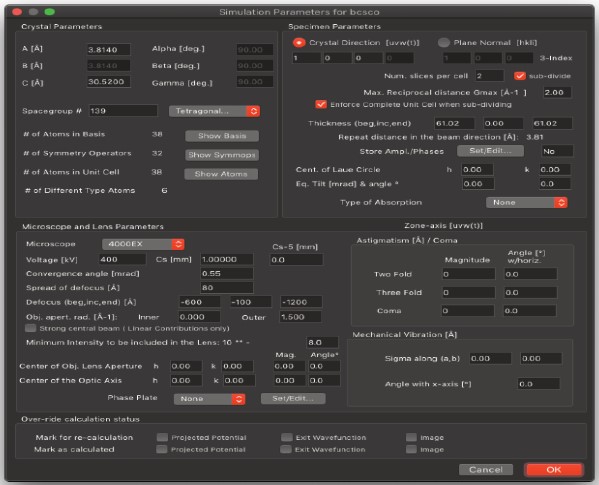
Spacegroup # 139
- 構造情報から、セルは正方晶で、空間群は I4/mmm であることがわかります。国際結晶学表の表 6.2.1 から、I4/mmm の空間群番号は 139 であることがわかります。ポップアップメニューから正しい空間群を選択してください。
a 3.814
- 格子定数 a の正しい値を入力してください。この例では、Tempas は正方晶空間群 #139 において b が a と等しいことを認識しているため、a を設定すると b が自動的に入力されます。同様に、Tempas は空間群によって定義されている単位胞角度を正しく入力します(この例では)。セルパラメータは nm ではなく Å 単位で入力することに注意してください。
c 30.52
- セルパラメータ C の値は Å 単位で入力します。
Gmax(default=2)
- 構造情報から、セルは正方晶で、空間群は I4/mmm であることがわかります。国際結晶学表の表 6.2.1 から、I4/mmm の空間群番号は 139 であることがわかります。ポップアップメニューから正しい空間群を選択してください。
Zone Axis 0,1,0
- 正しい応答は、試料に対する電子ビームの方向(または入射電子ビーム方向に対する試料の向き)を定義する3つの整数の集合です。この例では、試料をb軸に沿って撮像するために、0,1,0と入力します。
単位セルあたりのスライス数(デフォルト=1)
Number of slices per unit cell (default=1)
- この値は、Tempasによってビーム方向の構造の繰り返し距離と現在のGmax値から計算されます。この数値は必要に応じて変更できます(もちろん、この章に記載されているプロンプトに応じて入力するすべてのパラメータも同様です)。
Show Basis
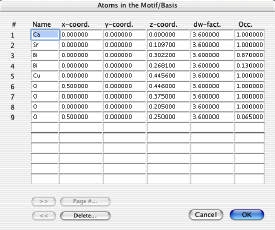
- コマンドをクリックすると、基底構造の原子数に関する情報を入力するためのダイアログボックスが表示されます。基底構造の原子について、9つの異なる原子位置を入力します。
Tempasは、基底構造の各原子について、化学記号、x,y,z座標、DW係数、占有係数を必要とします。上記の情報から、構造基底構造に与えられた9つの原子について、以下の情報を使用します。
| Chemical Symbol | Ca |
| x,y,z | 0,0,0 |
| Debye-Waller Factor | 3.6 |
| Occupancy | 1 |
最初の原子のデータには、カルシウムの化学記号(Tempasが適切な散乱係数テーブルを選択するために使用)、原子座標、温度係数(またはデバイ・ワラー係数)、および占有係数が含まれます。
| Chemical Symbol | Sr |
| x,y,z | 0,0,0.1097 |
| Debye-Waller Factor | 3.6 |
| Occupancy | 1 |
2番目の原子位置も同様に入力します。
応答は以左図のとおりです。
| Chemical Symbol | Bi |
| x,y,z | 0,0,0.3022 |
| Debye-Waller Factor | 3.6 |
| Occupancy | 0.87 |
3番目の原子位置も同様ですが、占有率は0.87に設定されます。
9つの原子位置をすべて入力したら、Tempasはシミュレーションを計算する電子顕微鏡のパラメータが必要になります。
Microscope 4000EX
- 入力した顕微鏡名がTempasに保存されている顕微鏡データに記載されている場合、様々な動作パラメータが自動的に設定されます。入力された顕微鏡名がTempasに認識されていない場合は、各動作パラメータの値を指定する必要があります。この例では4000EXを使用し、Tempasは球面収差係数を1.0mm、ガウス焦点深度半値幅を80Å、ビーム収束半角を0.5ミリラジアンに設定しています。
SpecimenThickness 40 20 80
- 箔厚の応答は、オングストローム単位の単一の値、または開始厚さと終了厚さを増分値と組み合わせた構成の2つの形式のいずれかになります。入力した構成は、Tempas に 40Å から 80Å まで 20Å 刻みの厚さの回折結果を保存するように要求します。つまり、試料の厚さが 40Å、60Å、80Å の場合です。
Store Ampl./Phases No
- Tempas は、指定された試料の厚さにおけるすべてのビーム振幅を保存するだけでなく、厚さの単一スライス増分ごとに選択したいくつかのビーム振幅を保存し、保存されたビームのいずれかについて、振幅(または強度)と位相を厚さの関数としてプロットすることができます。プロット用にビームを保存するには、コマンドをクリックして、保存する反射のインデックスを入力します。この最初の例では、ここでは何も情報を入力しません。
Voltage (400)
- 未知の顕微鏡タイプを選択した場合は、電圧を入力する必要があります。4000exを選択したので、Tempasは400keVの値を選択します。
Center of the Laue Circle 0,0
- ラウエ円中心として指定された2つの値は、Tempasによって、上記で指定された正確な晶帯軸方位から試料が傾斜する方向と量を定義するために使用されます。実際には、回折面のh座標とk座標の単位でラウエ円の中心を指定します。指定する値は整数である必要はありませんが、数度を超える傾斜を定義してはならないことに注意してください。デフォルト値の0,0は、正確な晶帯軸方位を指定します。
Objective Lens Defocus -200 -200 -800
- ここまでで、Tempas がシミュレーションの動的回折部分を実行するために必要なすべての情報を提供しました。次に、撮像条件を入力します。最初の撮像条件プロンプトは、対物レンズのデフォーカスです。-200Åから-800Åまでのデフォーカス値を-200Å刻みで指定することにより、4つのデフォーカス値を入力することを選択します。負の値は、ガウス条件から弱められた対物レンズ、つまりアンダーフォーカスが負であることを示します。
Aperture Radius 0.5
- 対物絞りの半径の値は、絞りを重ねて露光した回折パターンから測定された、オングストロームの逆数で表した半径に対応する必要があります。ここでは、分解能2.0Åを表すために0.5を入力します。
Center of theObjective Aperture 0,0
- 暗視野像をシミュレートするために、Tempas は回折パターンの中心からずれた対物絞りを提供します。ラウエ円中心については、絞り中心は h と k の単位で定義されます。デフォルト値は 0,0 のままにします。
Center of the Optic Axis0,0
- 顕微鏡のミスアライメントやビーム傾斜撮像条件に対応するため、光軸が位置する回折パターンの座標を、絞りの中心と同じ方法で指定できます。ここでも、デフォルト値の 0,0 を使用します。
- 上部のフィールドのすべてのデータが適切であれば、パラメータメニューの「原子を表示」に進み、すべての原子パラメータが正しく入力されていることを確認します。この段階で、コマンドメニューから「原子モデルを描画」を選択し、Tempas で構造モデルを表示させるのも有効です。
- すべてのデータが正しいことを確認したら、計算メニューの「完全計算」をクリックしてシミュレーションを実行します。Tempas は、計算の現在のステータスをステータスウィンドウに表示します。
まず、Tempas は構造の位相格子を計算し(ステータスウィンドウにこれまでに生成された係数の数が表示されます)、次に試料の各スライスの動的回折を計算し(現在のスライス番号はステータスウィンドウに表示されます)、指定した 3 つの試料の厚さごとに 4 つの画像を計算します(画像番号はウィンドウに表示されます)。 - Tempas が計算を終了すると、結果(回折パターン、画像、回折図)を表示できます(ビーム振幅と位相プロットが保存されている場合は、それらも表示されます)。
計算終了時に、電位、出射波、またはシミュレーション画像が自動的に表示されます。スルーフォーカスシリーズの画像は画像スタックとして表示されます。複数の厚さがある場合は、厚さごとに別々の画像スタックが表示されます。 - 画像を表示するには、表示ウィンドウに移動し、「画像」を選択し、「表示」を選択します。Tempas は12枚の画像のうちどれを表示するか尋ね、要求された画像を画面中央に表示します。画像はポインタツールで移動できます。
- 12枚の画像すべてを同時に表示画面に表示するには、オプションメニューから「モンタージュ」オプションを選択します。ソースウィンドウに戻り、「表示」を選択します。
- モンタージュオプションに戻り、「モンタージュ」の選択を解除します。
- 画像と比較するために予測電位を表示するには、ソースウィンドウで「電位」を選択し、「表示」を選択します。
- 保存された試料の厚さにおける回折パターンを表示するには、ソースウィンドウで「Diffr.Patt」を選択し、「Display」を選択します。パターンのサイズを変更するには、オプションメニューから「Diffr.Patt」を選択し、異なるカメラ長を選択します。回折スポットのサイズは、メインパラメータで設定された発散角にも依存します。
マウスを使用してインタラクティブに回折スポットをドラッグしてカメラ長を変更したり、ゼロGスポットの周囲をドラッグして収束角を変更したりすることもできます。 - 画像のパワースペクトルを表示するには、ソースウィンドウで「Image」を選択します。どの画像を表示するかを選択し、オペランドウィンドウで「Fourier Transform」を選択します。最後に「表示」をクリックしてパワースペクトルを表示します。パワースペクトルのオプションは、回折パターンの表示オプションと同じです。回折パターンとパワースペクトルに描画される円は対物レンズの絞りに対応しており、回折オプションからオフにすることができます。
8. 弱位相物体近似
弱位相物体(WPO)近似は、特定の球面収差Csが与えられた場合に、異なる分解能レベルで特定の構造についてどのような情報が得られるかを調べるのに有用なツールです。
WPO近似については既に説明しており、ここでもその情報の一部を取り上げます。WPO近似には2つの重要な仮定があります。
電子の波動関数は次のように表すことができます。
![]()
ここで、Ψ(x,y)は点(x,y)における電子の波動関数、V(x,y)は同じ点における投影された静電ポテンシャルです。
σは電子と原子のポテンシャルとの間の相互作用パラメータ、tは試料の厚さです。この最初の近似は、軽い原子を含む非常に薄い試料に適しています。
レンズX(u)によって引き起こされる位相シフトを考慮すると、
![]()
理想的なシェルツァーレンズとは、gベクトルが1/分解能以下の回折ビームをすべて透過し、gベクトルが1/分解能より大きい回折ビームをすべて遮断するレンズです。さらに、レンズを通過するすべてのビームに、中心ビームに対して90度の位相シフトを加えます。これは、散乱イベント自体によってもたらされる90度の位相シフト(上記の式の「i」)に加えて、レンズを通過するすべての散乱ビームが中心ビームに対して180度位相がずれる原因となります。
上記の2つの仮定の下、WPO近似におけるフーリエ空間における像強度は次のように表すことができます。
![]()
ここで、umaxは像に含まれる最大の逆間隔です。
Fはフーリエ変換を表します。空間周波数が所定の周波数で帯域制限された後、像強度は次のように表すことができます。
![]()
これは、弱位相物体近似とシャーツァーレンズの下では、原子の位置である静電ポテンシャルの高い領域で像強度が低いことを示しています。原子番号の大きい原子は、像の中でより大きく暗い領域として現れます。このタイプの像は、多くの場合、シャーツァー焦点ずれの薄い試料の同等の分解能を得るために、フルマルチスライス計算によって計算された像と外観が似ています。
WPO近似は、マルチスライス計算と同じ方法でメニューバーから呼び出されます。 WPO計算への入力は、開始分解能(Å単位)と終了分解能です。分解能のステップ数は、固定(ユーザー設定)または自動に設定できます。自動ステップを選択した場合、プログラムは1/開始分解能以内にある反射に対応する最初の画像を計算し、終了分解能に達するまで、より高い分解能に対応する次の反射セットについて新しい画像を計算します。
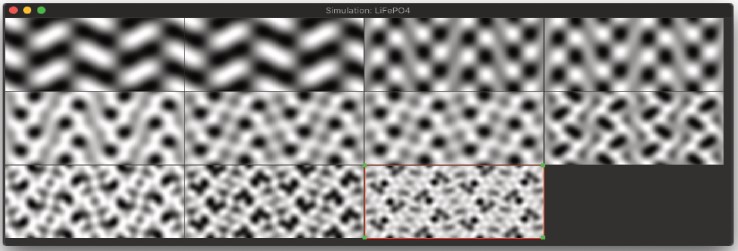
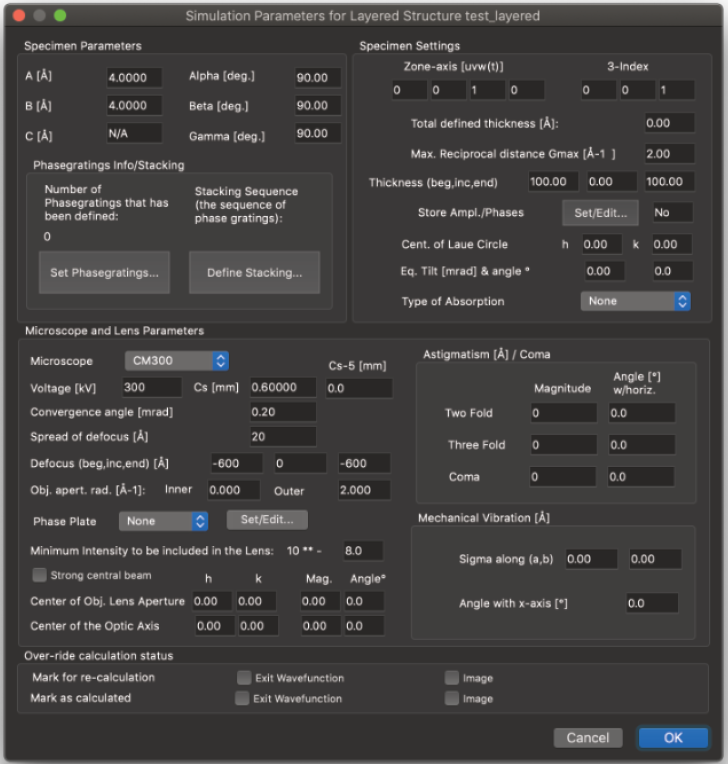
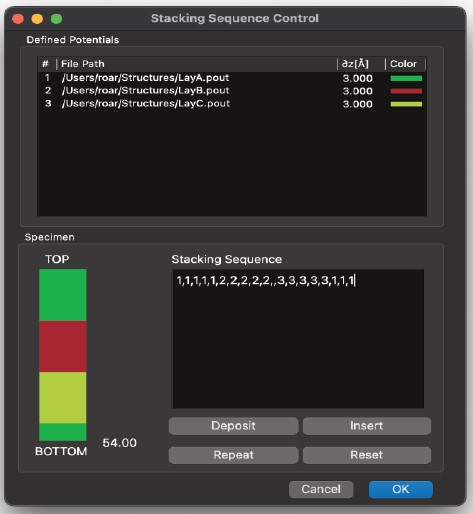
9. 階層構造の作成
層状構造とは、電子ビームの方向に沿って組成が変化する特殊な「構造」です。例としては、非晶質材料の表面層を持つ結晶性材料が挙げられます。また、電子ビーム方向の繰り返し間隔が長すぎて、繰り返し間隔をスライス厚として使用できず、単位胞を原子含有量の異なる複数のスライスに分割しなければならない結晶性構造も挙げられます。例として、LayAと呼ぶ3つの層を取り上げます。
LayBとLayCです。これらの各「層」は、いわゆる「単一」構造です。つまり、格子定数と原子組成を持つ単位胞として定義されます。共通点は、電子ビームに対する格子定数AとBが同じであり、それぞれ同一のサンプリングを使用することです(右図を参照)。
層状構造の考え方は、3つの層を任意の順序で配置して全体構造を構成できるというものです。「層状」構造の画像を作成および計算する手順は次のとおりです。
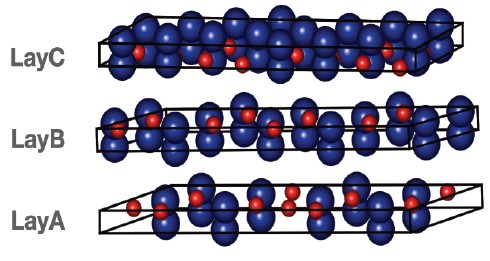
1) 3つの層LayA、LayB、LayCを、電子ビーム(AとB)に垂直な方向の単位胞寸法が同じ単一構造として定義します。
2) Gmaxに同じ値を使用して、各構造LayA、LayB、LayCの位相格子を計算します。
3) Tempas で「新規層状構造」オプションを使用して新規構造を作成します。格子定数 A や B などの情報を入力するよう求められます。層状構造には原子情報自体がないため、原子に関する情報は入力不要です。試料の厚さを入力するよう求められますが、構造の内容が定義されていないため、この時点ではこの値は意味を持ちません。A と B の値は、LayA、LayB、LayC の構造から取得されます。層状構造を作成すると、デフォルト値として 2 Å-1 が与えられます。LayA、LayB、LayC の位相格子の計算で異なる値が使用された場合、メインパラメータでこの値を変更する必要があります。
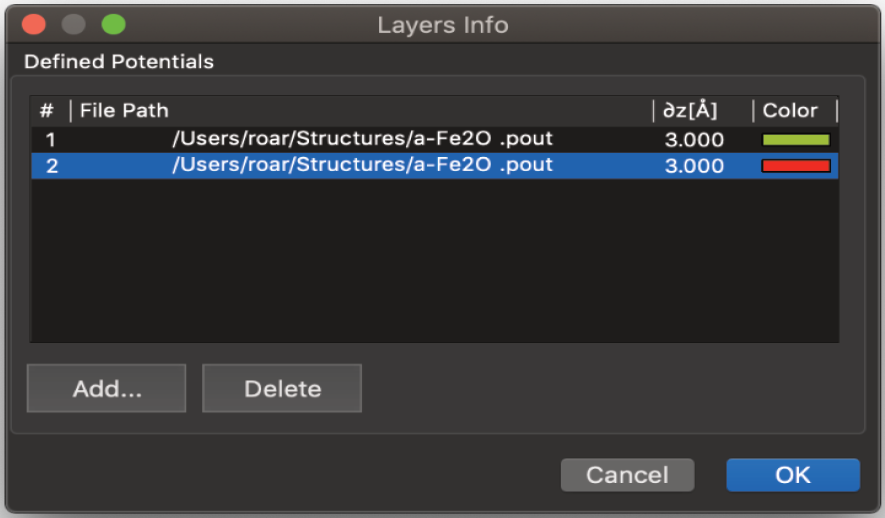
4) 3) の情報を入力するとファイルが作成され、層状構造の「構造」または「位相格子」の内容を定義する必要があります。これは「位相格子の設定…」コマンドを使用して行われます。
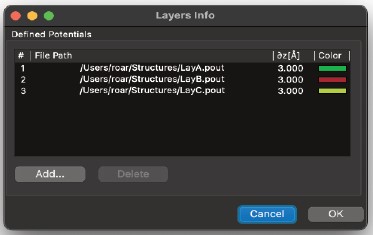
新規ファイルの場合、位相格子はリストに表示されません。レイヤーを定義するには、「追加…」コマンドを使用する必要があります。使用可能な位相格子ファイル(.pout)のリストが表示されます。LayA.poutをダブルクリックし、LayA.poutの計算に使用したスライス厚の値を入力します。
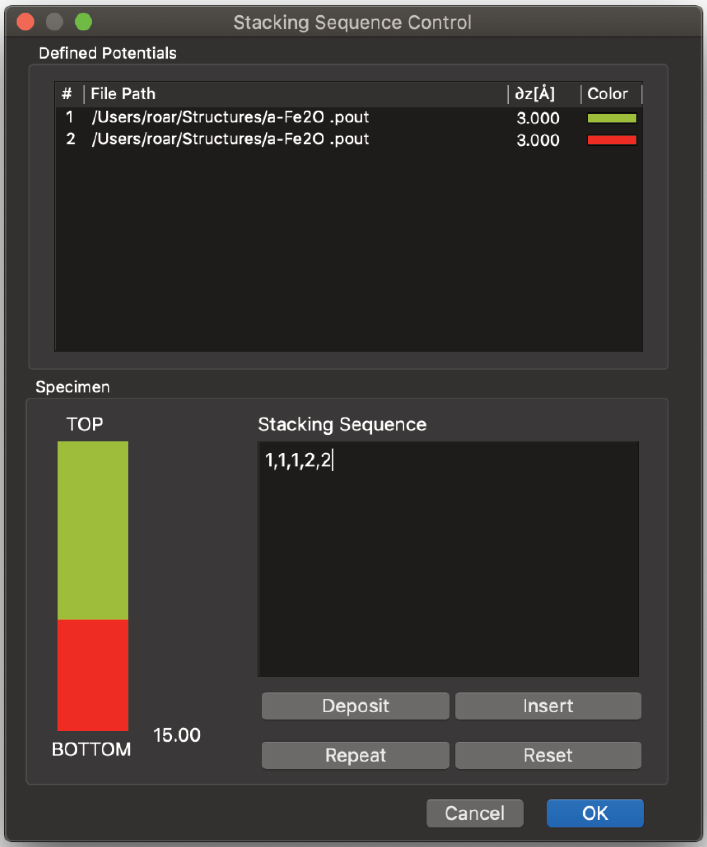
LayBとLayCについても同様に繰り返します。
これで、プログラムは使用可能な位相格子の情報を取得しました。最後に、「スタッキングの定義…」ボタンを使用してシーケンスを定義します。シーケンスは複数の方法で定義できます。1つの方法は、シーケンスを次のように入力することです。1,1,1,1,1,1,2,2,2,2,2,2,3,3,3,3,3,1,1,1 ここで、1はLayA、2はLayB、3はLayCを表します。コマンドを使用してシーケンスを定義することもできます。試料は常に左側に色付きのバーとして描画されます。これで構造の定義が完了します。
5) 次に、メインパラメータをチェックしてすべてが正しいことを確認し、最後に計算を実行します。計算はマルチスライスから開始されます。
10. 幾何学的位相解析
背景
幾何位相解析ルーチンは、特定の逆格子周波数付近の変化を解析することにより、参照格子に対する変位とひずみを求めます。
多くのルーチンは、階段ロッド計算のHRTEM像の例を用いて説明します。
解析対象の画像を最前面のウィンドウに表示した状態で、メニューから「幾何位相解析」を呼び出します。

| ※ 注意: 1) 画像は正方形である必要があります。または、分析する画像には、上記の基準を満たす選択範囲が存在する必要があります。 2) デフォルトでは、プログラムは自動的に画像のフーリエ変換を計算し、「現在の表示画像」として設定します。元の画像は、「現在の表示画像」プルダウンメニューから選択することで表示できます。 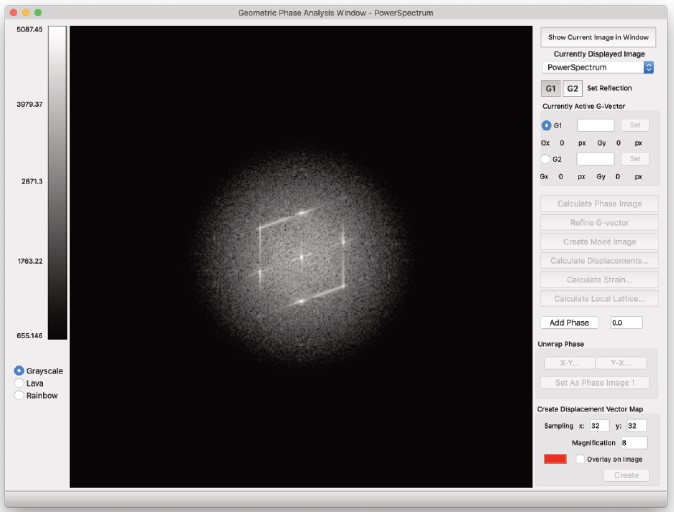 |
位相画像の作成
このルーチンは、選択された反射に関連する幾何学的位相およびその他の画像を計算します。
実行される計算は、元の画像のマスクされたフーリエ変換の逆フーリエ変換です。問題のマスクは、以下に定義されるタイプのマスクであり、逆空間周波数 g を中心としています。
振幅画像 A(r) と位相画像 P(r) = -2πg.∂u(r) が生成されます。
位相から 2πg.r の項が差し引かれており、これは原点を反射 g の位置に移動することと同等です。
∂u(r) は、周波数 g で定義される格子面に対する変位場です。
あらゆる場所の局所値を計算するには、次のようにします。
g(r) = -∂/∂r P(r) + g
使用方法:
1) G1ツールまたはG2ツールのいずれかを使用してGベクトルを選択する必要があります。
「位相画像計算」ボタンが有効になります。反射をクリックすると、選択した反射の周囲に円が描かれます。マスクのサイズは、描かれた円の半径によって決まります。半径は、ハンドルを操作するか、希望する半径を入力して「設定」ボタンをクリックすることで変更できます。
2) メニューコマンド「位相画像計算…」を呼び出します。
3) 位相画像を作成するためのオプションを示すダイアログが表示されます。
Options:
マスク
マスクの種類として以下の選択肢があります。
- シャープな円形マスク
M = 1, r <= R, M = 0, r > R - ソフトな円形マスク(ガウスエッジを使用、半値幅は半径の1/5)
M = 1, r < 0.8R M = exp{- (r-0.8R)2/sigma2} r >= 0.8R, sigma = 0.2R - ガウスマスク(exp(-r2/sigma2))
出力
幾何学的位相画像を保持(デフォルト)。通常はこれで十分です。
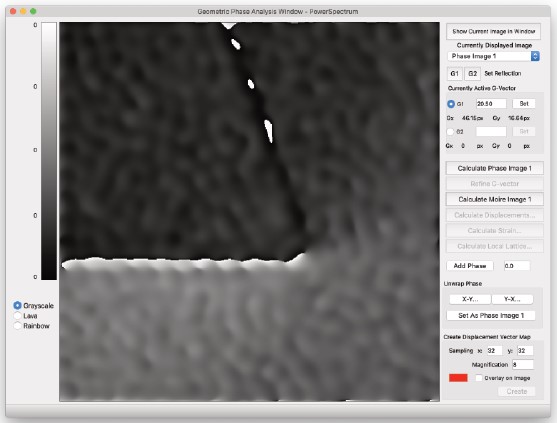
局所gベクトルを計算して表示します。
これは、画像内の各点におけるg(r)のx成分とy成分を含む2つの画像を計算します。
振幅画像を保存して表示します。
振幅画像と位相画像を計算するマスクされたFTを保存して表示します。
結果の位相画像は、項を減算することで計算されます。
ここで、g0はパワースペクトルのピーク強度の位置を求めて返された値です。
結果の画像は、デフォルトでPhase ImageとAmplitude Imageという名前が付けられます。
| ※ 注意: 1) 位相像を計算した後、次に行う操作は、局所gベクトルを改良することです。これは、位相像内で格子間隔が一定とみなされる領域を選択し、メニューコマンド「局所平均gベクトルの検出」を呼び出すことによって実行されます。これは、この方法で求められた間隔が、後続の計算の基準となることを意味します。 2) 変位とひずみを計算する前に、2つの非共線周波数g1、g2を定義する必要があります。 3) g1を改良した後、次のステップは、前のステップと同じ方法でG2ツールを使用してg2を設定し、g2を改良したときと同じ領域の局所ベクトルを改良することです。 |
局所gベクトルの調整
背景:
変位やひずみを計算するには、参照格子が必要です。前のコマンドで位相画像を作成したときに検出されたベクトルgは、振幅が最も大きいベクトルであり、必ずしも参照格子として選択したいベクトルとは限りません。ベクトルgをさらに調整するには、選択ツールで、平均格子間隔を計算するための参照領域となる領域を選択します。
参照格子を定義するには、同じ領域に対して調整する必要がある2つのベクトルg1とg2が必要です。
使用方法:
選択ツールで、平均gベクトルを求めたい領域をマークします。
「局所平均gベクトルを求める」コマンドを実行します。このコマンドは、選択領域内に減算すべき残差ランプ2π∂g.rがあるかどうかを判定します。補正値∂gは、「位相画像を計算…」で求められたベクトルgに加算されます。このルーチンは、位相ジャンプのために最初の選択範囲を小さくする必要がある場合、徐々に大きな選択範囲を使用することで、ベクトルgを改良するために繰り返し使用できます。
下の画像は、平均局所gベクトルを求めるために使用する領域を選択範囲でマークした元の位相画像を示しています。右側には、操作の結果が表示されています。
| ※ 注意: 前述のように、2つのベクトル g1 と g2 は参照格子を定義するために使用されます。通常、このコマンドは位相画像が計算される各ベクトル g に対して使用され、その位相画像は位相画像 #1,2 として参照されます。 |
位相の追加
このルーチンは、画像「位相画像」に一定の位相を追加します。通常の操作では、このコマンドは使用されません。位相が2πを超える際に生じるラップアラウンド効果に伴う不連続性を除去するために使用できます。
モアレの作成
使用方法:
このルーチンを使用して、画像「位相画像」から計算されたモアレ画像を作成します。これは、逆空間逆FFTの原点を、原点から空間周波数gへの線に沿って点|g|/Mに移動することと同等です。数学的には、モアレ画像は
P(r) = 2πg.r/M -2πg.∂u(r) となります。ここで、Mはダイアログボックスで選択した倍率です。
M -> ∞は、「位相画像の計算」コマンドで計算された幾何学的位相画像です。
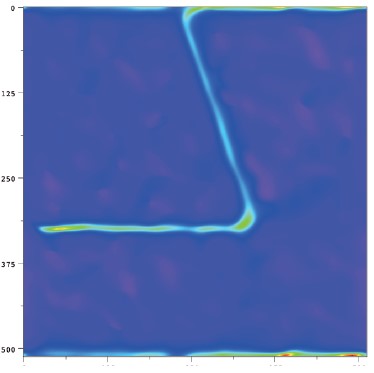
変位計算
このコマンドを実行すると、2つの画像 ux と uy が生成されます。これらは、g1 と g2 で定義された格子に対する局所的な x,y 変位です。
このコマンドを実行するには、「Phase Image 1」と「Phase Image 2」という2つの画像と、それらに対応する g1 と g2 の値が必要です。
このコマンドを実行すると、以下のダイアログボックスが表示されます。
操作の結果として以下の出力が生成されます。
前提条件:
このコマンドを実行する前に、g1 と g2 の両方、およびそれらに対応する画像「Phase Image 1」と「Phase Image 2」が存在している必要があります。
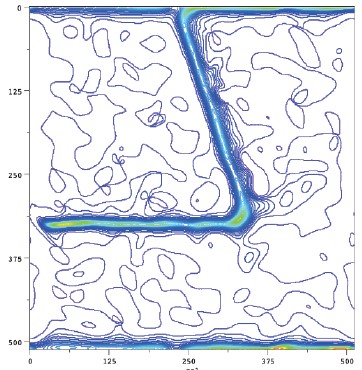
以下は、x 変位をベクトルの x 成分の長さ、y 変位をベクトルの y 成分としたベクトルプロットです。
データは、変位の大きさを示す面プロットとしても表示できます。
あるいは、変位の大きさは、下図のように等高線図として表示することもできます。
ひずみ計算
このコマンドは、g1とg2で定義された参照格子に対するひずみを計算します。
前提条件:
2つの位相画像「位相画像1」と「位相画像2」が計算されている必要があります。
結果:
要求された出力に応じて、結果は以下のいずれか、または複数になります。
a) 変形マトリックス
b) 対称ひずみマトリックス
c) 回転角
d) 主ひずみ成分
次ページの画像は、主ひずみ成分e1とe2を計算して表示するように選択した場合の出力を示しています。e1のx成分とy成分、およびe2のx成分とy成分の4つの画像が生成されます。
手順:
プログラムはまず変形行列を計算します。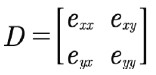
これは、点r’ (x’,y’)の位置と、その非ひずみ位置r (x,y)の関係を表わします。
![]()
行列Sは、対称行列S’と回転行列Wに分解されます。
 and
and 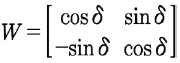 with
with 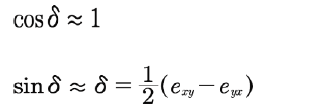
こうして対称ひずみ行列が得られ、
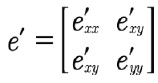
計算された3つの成分が画像として表示されます。
2つのベクトルe1とe2も計算され、画像e1x、e1y、e2x、e2yが表示されます。これらはそれぞれ、2つの主ひずみベクトルのx、y成分です。
局所格子の計算
このコマンドは、画像内の異なる点における局所格子パラメータ a と b を計算します。各点における g1 と g2 の局所値と、2 つの反射のミラー指数を用いて、ベクトル a と b によって与えられる格子を参照します。y 座標は、環境設定での設定に応じて、画像座標 (0,0 左上) または通常の座標系 (x,y) を参照できます。
前提条件:
ベクトル g1 と g2 の両方と、それぞれの位相画像(位相画像 1 と位相画像 2)が設定されている必要があります。
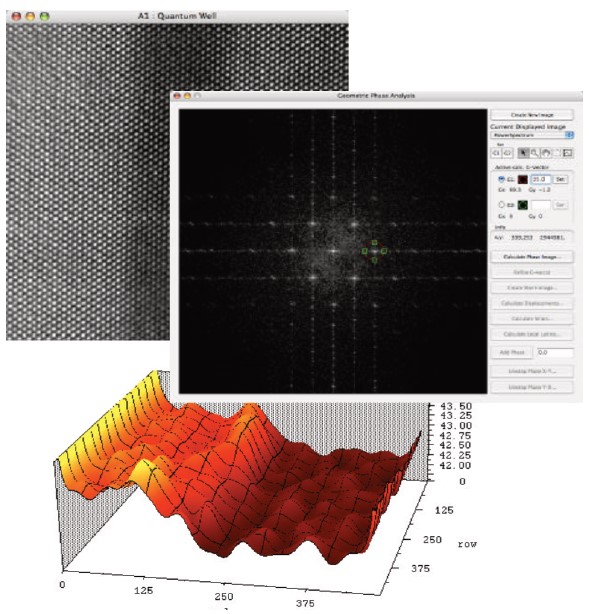
例
以下の画像は、In(Ga)N 量子井戸の HRTEM 像に対するルーチンの使用例を示しています。左の画像は HRTEM 像、右の画像はパワースペクトルと格子計算に使用した反射の 1 つを示しています。一番下の 3 番目の画像は、画像内の位置の関数として a 格子パラメータをプロットした表面プロットです。
位相 (x,y) のアンラップ
コマンド「位相(x,y)のアンラップ」は、画像「位相画像」の位相をアンラップします。
ユーザーは開始位置の入力を求められます。開始位置に対応する位相が、その時点で割り当てられます。ルーチンはまず各行に沿って移動し、位相値の連続性を維持しようとします。π-∂から-π+∂へのジャンプではなく、位相はπ+∂の値を取り、位相ジャンプを通過する際に増加または減少を続けます。
このコマンドは、まず画像の行を処理し、次に列を処理します。
位相 (y,x) のアンラップ
コマンド「位相(y,x)のアンラップ」は、画像「位相画像」の位相をアンラップします。
ユーザーは開始位置の入力を求められます。開始位置に対応する位相が、その時点で割り当てられます。ルーチンはまず各列に沿って移動し、位相値の連続性を維持しようとします。 π-∂から-π+∂へのジャンプの代わりに、位相はπ+∂の値を取り、位相ジャンプを通過するときに増加または減少し続けます。
このコマンドは、まず画像の列を処理し、次に行を処理します。
11. HRTEM画像から焦点を見つける
背景
十分な量の非晶質材料が存在する場合、HRTEM像のデフォーカス量は、そのパワースペクトルから決定できます。
これらの条件下では、対物レンズが薄い非晶質材料を通過する散乱電子に及ぼす影響から生じるパワースペクトルの特徴を記述するために、弱位相物体近似を適用できると仮定しました。弱位相物体近似では、HRTEM像のパワースペクトルは、右図の式に比例します。

非点収差がなく、焦点の広がり(時間的非一貫性)と輻輳(空間的非一貫性)の影響を無視すると、パワースペクトルの強度はほぼ右図の式に比例する。
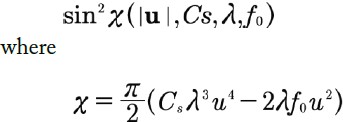
これは、パワースペクトルに常に極大値が存在することを示しています。
n = 奇数のとき
したがって、球面収差が既知であれば、パワースペクトルの極大値の位置を見つけ、様々な極大値(リング)にインデックス(n)を割り当て、焦点(f0₎)を解くことで焦点を決定できます。
パワースペクトルに複数のリングがある場合、各リングから得られる焦点の値は異なり、焦点は平均値と標準偏差で表されます。
これらのルーチンを使用する前に、HRTEM像から焦点を計算する際に使用する顕微鏡パラメータを指定する必要があります。設定する必要があるパラメータは、「顕微鏡電圧」と「対物レンズ球面収差定数」です。
さらに、プログラムは画像のパワースペクトル内のリングの探索とリングのインデックスの割り当てにいくつかのパラメータを使用します。プログラムの使用を通してパラメータの影響をより深く理解できるようになるまで、まずはデフォルトのパラメータを受け入れます。
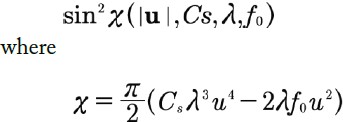
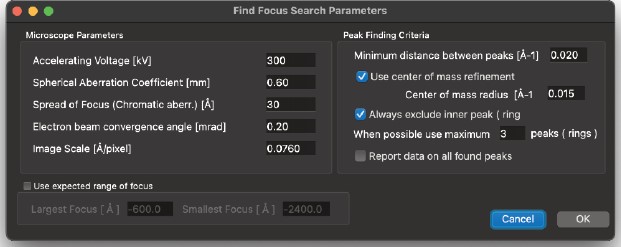
顕微鏡パラメータ
電圧
- これは顕微鏡の加速電圧(kV)です。顕微鏡のコントラスト伝達関数を決定する際に使用されます。
球面収差
- これは対物レンズの球面収差係数(mm)です。顕微鏡のコントラスト伝達関数を決定する際に使用されます。
デフォーカスの広がり
- これは、対物レンズの色収差と、加速電圧、レンズ電流、およびフィラメントから放出される電子のエネルギーの変動によって生じるデフォーカスの実効的な広がりです。Å単位で表され、顕微鏡のコントラスト伝達関数を決定する際に使用されます。
収束角
- これは、試料に入射する電子の円錐の半角(ミリラジアン)です。顕微鏡のコントラスト伝達関数を決定する際に使用されます。
ピーク検出基準
- パワースペクトルにおけるリングの最大値を検索する際、プログラムは調整可能なパラメータを用いて不要なピークを除外し、リングの「正確な」位置を決定します。
ピーク間の最小距離
- 2つのピークがÅ-1で指定された距離よりも近い場合、小さい方のピークは破棄されます。
- 指定された距離内の質量中心(強度)を使用します。
質量中心を使用するオプションを選択した場合、指定された距離内のÅ-1の強度を使用してピーク位置を精緻化し、新しいピーク位置を取得します。 - 検出されたすべてのピークを報告
このオプションが設定されている場合、プログラムは検出されたすべてのピークのデータを出力します。2つのピークがÅ-1で指定された距離よりも近い場合、小さい方のピークは破棄されます。
フォーカス決定基準
- リングのインデックス割り当てにおいて、最初のリングが許容フォーカス値の範囲内にあるフォーカスを与える場合、最初の極大値にはインデックス1が割り当てられます。許容フォーカス値の範囲内に収まらない場合、プログラムはパワースペクトル内の次の極大値に進みます。次のリングにはインデックス3、5、7、…が割り当てられます。通常、最初のリングは、その極大値の位置に関する不確実性が大きく、そのオプションが設定されている場合(デフォルト)、プログラムは最初のリングから得られたフォーカス値を使用しません。
最初のリングを除外
- このオプションを選択すると、プログラムは平均フォーカス値を求める際に、最初のリングから計算されたフォーカスを含めません。
最大リング数を使用する
- プログラムは多くの極大値を見つける可能性があり、それらをフォーカス決定に含めるべきかどうかに関して不確実性が増します。プログラムは指定された数を超えてリングを使用しません。
フォーカス範囲
- プログラムはこの範囲を使用して、特定のピークが疑似ピークであり、リングインデックスの割り当てに使用すべきでないかどうかをアルゴリズムが判断できるようにします。
画像からフォーカスを検出
これは、1枚のHRTEM画像からフォーカス値を検出しようとします。
フォーカスの検出精度は、画像の解像度、フーリエ変換領域のサイズ(逆格子空間における解像度)、パワースペクトル内のリングの数(フォーカス値)、画像内に存在するアモルファス物質の量など、多くの要因に依存します。
手順:
画像が既にキャリブレーションされている場合、またはキャリブレーションが既知でない限り、まず作業対象の画像をキャリブレーションする必要があります。
直線定規ツールを使用して、HRTEM画像に既知の寸法の線を作成し、その線をキャリブレーションします。
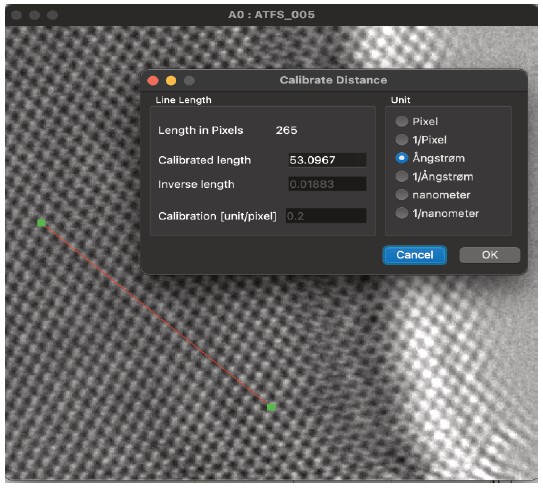
ルーチンが動作するには、キャリブレーション単位はÅまたはnmである必要があります。
これが完了したら、2の累乗の寸法を持つ正方形の領域を選択します(領域を選択する際はOptionキーを押したままにします)。この領域には、非晶質領域が含まれます。この例では、1024ピクセルの画像のうち、512の正方形領域が該当します。選択範囲が設定されていない場合、ルーチンは画像全体を使用します。この特定の例では、256の正方形領域を選択すると、逆格子空間でのサンプリングが不十分になり、良好な結果が得られません。
「画像からフォーカスを見つける」コマンドを実行する前に、画像内に選択範囲が1つだけ設定されていることを確認してください。
コマンドを実行すると、次の結果ウィンドウが表示されます。
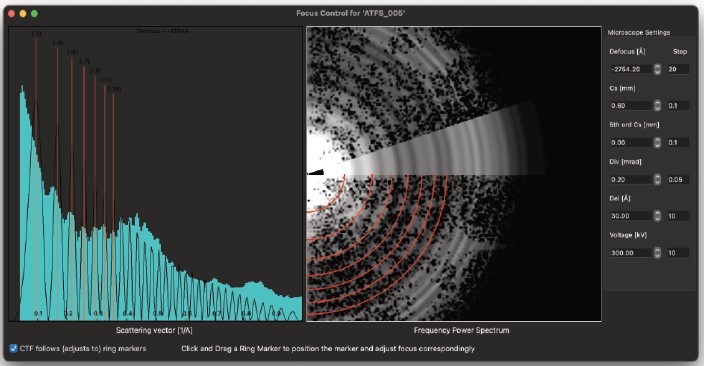
プログラムは、非晶質含有量に関連するパワースペクトルを半径(逆距離)の関数として計算します。これは、各半径におけるパワースペクトルの振幅の中央値を算出することで行われます。中央値は青緑色でプロットされ、実験データに対応します。1次元データセットのピークが検出され、リングのインデックスが割り当てられます。各リングから焦点が計算され、焦点(デフォーカス)の平均値を使用して、仮想的なコントラスト伝達関数CTFが計算されます。
![]()
CTFは、リストされた値に基づいて次のようにプロットされます。
CTFの最大値は、マウスでドラッグできる垂直マーカーで示されます。マーカーをクリックし、マウスを押したままにすると、最大値の位置を変更できます。すべての最大値が変化し、それに対応する焦点の値が表示されます。インセットとして、実験的なパワースペクトルと、プログラムがリングを見つけるために使用する平均データを示す領域が表示されます。実験データには、現在の焦点値に対応するリングが重ねて表示されます。マーカーを動かすとリングの位置が変わり、ユーザーは手動で焦点値に最適な値を求めることができます。
12. ホルツ相互作用とサブスライス法
適切なアルゴリズムを用いることで、回折計算にゾーン外散乱や非ゼロ(または高次)ラウエゾーン(HOLZ)相互作用の効果を考慮することができます。基本的に、「マルチスライス」結晶を記述する位相格子(または投影ポテンシャル)のセットを生成する方法は4つあります。ビーム方向の繰り返し距離が短い構造の場合、最も簡単な方法はユニットセルごとに1つのスライスを使用することです。ビーム方向の繰り返し距離が大きい構造の場合、いくつかの方法が使用できますが、そのうち3つはスライスを「サブスライス」に分割する方法です。Tempasでは、4つの方法のいずれも使用できます。
単位セル繰り返し距離あたり1つのサブスライスのみを持つ同一スライス
すべてのスライスが同一のマルチスライス計算では、入射ビーム方向に沿った構造の変化に関する情報は含まれず、ゼロ次ラウエゾーン(ZOLZ)層との散乱相互作用のみを考慮します。ビーム方向の繰り返し距離が短い構造の場合、エワルド球は(比較的遠い)高次ゾーンに近づかないため、このような計算で十分です。
単位セル繰り返し距離あたりn個のサブスライスを持つ同一サブスライス
ビーム方向の繰り返し距離が大きい構造の場合、電子散乱を十分な精度で計算するためには、スライスを細分化する手法が必要です。最も単純ですが、最も近似的な方法は、全繰り返し周期の投影ポテンシャルを計算し、投影ポテンシャルの1/nを用いて、スライスを完成させるためにn回適用できる位相格子関数を作成することです。この方法は「擬似上層線」(Goodman and Moodie, 1974)との相互作用を回避しますが、実際のHOLZ層は無視します。
原子位置に基づくサブスライス
投影ポテンシャルの細分化の改良点は、単位胞の原子位置を細分化することです。この手順では、単位胞内の原子位置のリストを、入射ビーム方向における原子の位置に応じてn個のグループに分割します。これらのサブスライスされたグループから、異なる投影ポテンシャルが生成され、n個の異なる位相格子が形成されます。これらの位相格子は、スライス全体からの散乱を生成するために順次適用されます。
3次元ポテンシャルに基づくサブスライス
原子位置の細分化のさらなる改良点は、スライス全体の3次元ポテンシャルを細分化することです。これは、あるサブスライス内の位置にある原子は、次のサブスライスにまで広がるポテンシャル場を持つことができるためです。完全な3次元ポテンシャルを計算し、適切なサブスライスにわたって積分する代わりに(128x128x128のポテンシャルでは200万以上のサンプルを保存する必要がある)、サブスライスz0 ± ∂z内のポテンシャルをz0の平面に投影した解析式を導くことが可能です(Self et al., 1983)。この手法は、ビーム方向に大きな繰り返しを持つ構造に日常的に適用でき、連続的に適用するための複数の異なる位相格子を生成することができます。また、ビーム方向に非周期的で、多数の個別の非繰り返し位相格子を必要とする構造(おそらく欠陥を持つ)にも適用できます(Kilaas et al., 1987)。
Tempas のサブスライス
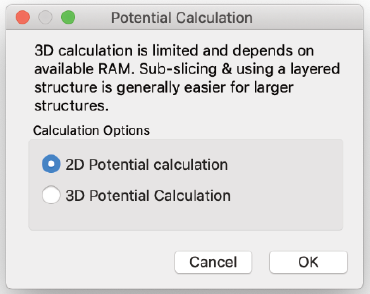
計算の精度を十分に維持しつつ、Tempas は通常、試料、ゾーン軸、加速電圧、最大 g の特定の組み合わせに対して、スライスの定義方法を指定する最も単純(かつ迅速)な方法を選択します。そのため、ユーザーは HOLZ 相互作用が重要でないと判断された場合は無視することができます。HOLZ 相互作用が重要な場合は、オプションメニューで「2DPotential 計算」ではなく「3DPotential 計算」ラジオボタンを選択してください。
2次元計算を選択した場合、ビーム方向のセル繰り返し距離が短い場合、Tempas はセルあたり1つのスライスを使用します。繰り返し距離がユニットセルあたり1つのスライスでは不十分なほど長い場合、Tempas は n 個の同一のサブスライスを作成することで擬似上層線を回避します。
3次元計算を選択した場合(3Dポテンシャル計算が有効)、繰り返し距離が大きい場合は細分化された3次元ポテンシャルを使用し、繰り返し距離が十分に短い場合はデフォルトでセルあたり1つのスライスを使用します。なお、ユニットセルあたりのサブスライス数は、パラメータメニューで明示的に設定することで1より大きくすることができます。これにより、繰り返し距離が短い場合でも HOLZ 相互作用が確実に考慮されます。もちろん、繰り返し距離が非常に短く、逆格子空間で HOLZ が離れている場合、計算とそれがモデル化する実験はどちらも HOLZ 反射と非常に弱くしか相互作用しません。
入射ビーム方向に層状または非周期的な構造からの散乱を生成するために「層状構造」オプションを使用することは、原子位置に基づくサブスライス法の応用に相当します。ユーザーは、選択した原子を異なる構造ファイルに割り当て、各サブスライスに位相格子を形成し、「位相格子のスタック」コマンドを使用してサブスライスをどのように使用して試料構造を記述するかを指定することにより、複数のサブスライスを作成できます。これは、上部ラウエ層を含める必要がある場合、または3次元効果が重要な場合に最初に試すことが推奨される方法です。完全な3D計算を使用するよりもはるかに高速です。
その他の手法
Van Dyckは、HOLZ層の効果を考慮するための他の手法として、ポテンシャル偏心を考慮した2次マルチスライス法(Van Dyck, 1980)や改良位相格子法(Van Dyck, 1983)を提案している。これらの手法の検証により、ポテンシャル偏心を考慮することで生じる追加の計算は有効である可能性があるものの、改良位相格子法は発散しやすく実用的ではないことが示された。
Goodman P, Moodie AF (1974) マルチスライス法による電子散乱におけるNビーム波動関数の数値評価.Acta Cryst. A30, 322-324.
Kilaas R, O’Keefe MA, Krishnan KM (1987) 高分解能透過型電子顕微鏡における計算手法への上層ラウエ層の組み込みについて. Ultramicroscopy 21, 47-62.
Self PG, O’Keefe MA, Buseck PR, Spargo AEC (1983) 電子回折における振幅と位相の実用的計算.
Ultramicroscopy 11, 35-52.
Van Dyck D (1980) 複雑結晶または無秩序結晶の構造像のシミュレーションのための高速計算手順:新しいアプローチ.J. Microscopy 119, 141-152.
Van Dyck D (1983) 高解像度電子顕微鏡写真のシミュレーションのための高速計算技術.J. Microscopy 132, 31-42.
13. 画像マッチングによる構造精密化
はじめに
HRTEM像のシミュレーションを行う目的は、これらの像を実験データと比較し、構造を決定することです。
実際には、様々なモデルが提案され、一致するまで像が計算されます。一致する像が見つかった時点では、構造(原子位置と原子番号)は、ある程度の不確実性をもって既知であると仮定されます。あるいは、与えられたモデルから始めて、実験とシミュレーションの適合度が最大となるように、モデルを体系的に変化させる方法もあります。これには、実験像と計算像を比較するための効率的な方法が必要です。
また、測定における不確実性(実験像における像強度)に関する知識と、この不確実性を化学組成および原子位置の不確実性と関連付ける方法も必要です。定量的電子顕微鏡法のこの分野は比較的新しいため、ほとんどの像は依然として目視で比較されています。しかしながら、これは活発な研究分野であり、統計学からの多くの手法がHRTEMで使用され始めたばかりです。
定量データの取得
電子顕微鏡写真から定量情報を抽出するには、データを数値で表現する必要があります。通常、TEM画像は、以下のいずれかの方法でデジタル表現されます。
i) 画像を写真乾板に記録し、スキャナーを用いてフィルムの濃度を数値に変換し、コンピュータに保存する。
ii) 画像をイメージングプレートに記録する。
iii) 低速走査CCDカメラで画像を記録し、蓄積された電荷をコンピュータに読み出す。
最初の方法では、フィルムの非線形応答のため、コンピュータの計算結果と直接比較できないデータが得られます。
しかし、露光時間を変化させながら制御された一連の露光を行い、得られた走査値を電子線量に対してマッピングすることで、フィルムの応答を較正することは可能です[1]。
イメージプレートとCCDカメラはどちらも電子線量に対して線形な数値を生成し、計算値と比較するためにはデータのスケーリングのみが必要です[2]。
上記の様々な記録媒体の相対的な利点については多くの議論があり、それぞれに独自の利点があります。CCDカメラは現在2K×2Kピクセルに制限されていますが、近い将来、複数のチップを使用することで6K×6Kまで到達できる可能性があります。変調伝達関数(MTF)を特性評価できるため、電子の広がりや隣接セルへの電荷の漏れ込みによる高周波応答の低下をデコンボリューションで簡単に補正できます[3]。
イメージングプレートはCCDカメラの多くの利点を備え、より広い画像領域をカバーします。しかし、イメージングプレートはCCDカメラほど普及していません。多くの研究室では、現在、フィルムの使用を継続しながらも、多くの記録をCCDカメラで行い始めています。
データの前処理
画像データが数値に変換されたら、必要なデータ処理や変換を行うことができます。必要なデータの前処理は、求める情報の性質によって異なるため、最適な方法は一つではなく、いくつかの選択肢があります。
データのサンプリングと再サンプリング
撮像システムまたは記録システムの動作によって、画像が視野全体で歪んでいる場合、画像のワーピング変換によってデータを再変換することができます。これは、完全に結晶性の物質を撮像し、原子が存在するとされる位置と撮像された位置との偏差を記録することで歪みを判断できる場合に行うことができます[4]。
Gatan Imaging Filterなどの一部のシステムでは、円形の穴の正方格子の画像を記録することで歪みを測定します。
結晶材料の画像は、格子相対座標上に再サンプリングすることができ、単位格子の寸法は整数個のピクセルで表され、最終画像の寸法と一致する。これにより、画像の周期的な連続性を表さない境界上のエッジによって画像が切り捨てられることで生じる、画像のフーリエ変換におけるストリーキングが除去される。ストリーキングは、画像に円形マスクを掛け合わせることで軽減できる。マスクは、指定された半径までは値1を持ち、画像の境界に近い5~10ピクセル以内では徐々に値0に減少する円状のピクセルで表される。マスク処理の副作用として、フーリエ変換におけるノイズが増加するが、これについては後述する。結晶材料の単一のユニットセルの画像のみを決定し、画像シミュレーション計算で得られた画像と比較する必要がある場合、ユニットセルの画像を計算に使用した座標系とサンプリング間隔に再サンプリングすることができます。これは、次の式で定義される行列Mを決定することと同等です。
as = Mae 1)
bs = Mbe
必要な手順は2つあります。1つは格子基底ベクトルを同一にするために必要な回転/スケーリング、もう1つは共通原点の決定です。
実験画像と計算画像の共通原点は、シミュレーション画像と実験画像間の相互相関によって決定されます[5]。
フーリエ変換とマスキング
結晶材料のHRTEM像のフーリエ変換は、格子間隔に関する有用な情報を提供し、実験的なフーリエ振幅と理論計算値の比較にも使用できます。変換される像がW(幅)とH(高さ)の周期関数となることはほとんどないため、純粋な結晶材料の像のフーリエ変換は、完全に周期的な信号(結晶)のフーリエ変換と像の寸法と同じサイズのウィンドウの変換との畳み込みとなり、ブラッグピークはウィンドウの変換の形状をとります。
マスクの使用はウィンドウの変換を変え、ピークプロファイルの減衰を速めるために使用できますが、ノイズレベルの増加を犠牲にします。これは上に示されており、1次元信号にマスクを適用した場合の効果を示しています[6]。これはまた、格子間隔を決定するためのピーク位置の特定や、フーリエ成分の振幅の推定にも影響します。両方の推定値の標準誤差はマスクの適用に応じて増加しますが、コサインウィンドウは良い妥協策となります。
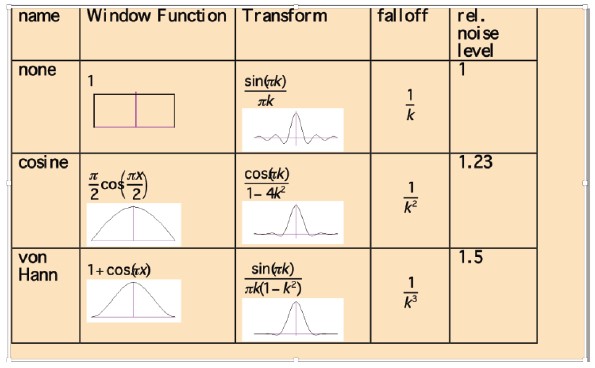
ノイズ低減
ノイズを低減することに加えて、存在するノイズ量を推定し、信号対雑音比(S/N比)を見積もることも重要です。2つの同等の領域から、2つの領域の相互相関係数を求めることでノイズを推定できます。相互相関係数ccfが与えられている場合、信号対雑音比は次のように推定できます。
2) 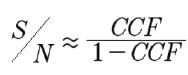
ノイズを低減し、単一のユニットセル(モチーフ)の画像の統計的平均を得るために、個々のモチーフの位置を相互相関によって決定することができます。これらが見つかったら、統計的に同等の領域を平均化して平均モチーフを見つけ、ユニットセル内の位置の関数として個々のピクセルに関連するS/N比を決定します。これにより各ピクセルiの標準偏差が決定され、実験的に平均化された画像と計算された画像とのマッチングに関連する信頼度レベルを設定するために使用できます[7]。
3) 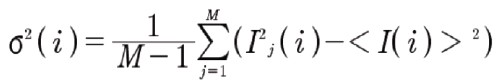
ここで、Mは平均化される同等の領域の数です。
ローパスフィルタを使用して画像を平滑化することは、ノイズレベルによっては効果的ですが、特に統計的に同等の領域の平均化が実行できない場合に効果的です。平滑化は目で特徴をより明確に認識するのに役立ちますが、画像ピクセル間に相関関係が生じ、シミュレーション不一致基準の有意閾値を歪める可能性があるという欠点があります。
平均化は対称化によっても実行できます。対称化とは、存在することが分かっている対称操作を実行したモチーフのコピーを平均化することです。これにより、M個の対称性関連コピーを平均化した場合よりもノイズレベルがさらに1/4に低減されますが、撮像条件の欠陥が隠れてしまう可能性もあります。
実験画像とシミュレーション画像のマッチング
2つの画像間の類似性または不一致を測定する方法は数多くあります。以下にそのいくつかを示します[8]。
平均二乗差:
4) 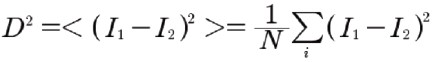
二乗平均平方根差:
5) ![]()
平均弾性率差:
6) 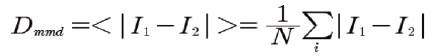
相互相関係数:
7) 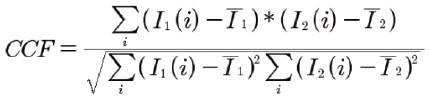
括弧 <> はすべて、括弧で囲まれた量の平均を示します。
これらの各式において、合計は画像内のすべてのピクセル i について行われ、N はピクセルの総数です。上記の相互相関係数は、画像が平均ゼロに正規化された正規化係数です。
CCF(差異ではなく類似性を測定する係数)は、2つのn次元ベクトル(nは画像内のピクセル数)間の外積として解釈することもできます。その場合、CCFに角度を関連付けることができます。これは、2つのベクトル間の内積の一般的な解釈において、角度が であることを意味します。この角度は、同一の画像ではゼロです。上記の正規化相互相関係数の定義のように、画像が平均ゼロで単位長さに正規化されている場合、角度は180度です。 2つの画像I₁とI₂のコントラストを反転させます。
有意性とノイズ
上記の各基準は、測定値の有意性について検定する必要があります。
D²は、どちらの画像でも平均二乗強度(またはノイズによる強度偏差)と比較できます。
Drmsは、どちらの画像でも強度の標準偏差と比較できます。
2つの画像間の不一致を検定する良い方法は、画像のノイズが分かっている場合に、2つの画像が等しい確率を統計的に表す尺度を使用することです。実験画像の各ピクセルに相関のないガウスノイズがあると仮定すると、最適な統計的尺度は次式で与えられます。
8) 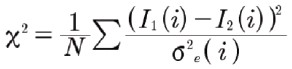
ここで、Nは画像内のピクセル数です[9]。この値はピクセルiに関連付けられた標準偏差であり、上記のように、複数の同等の領域から求めることができます。実験画像Ieを計算画像Icと比較し、計算にM個の調整可能なパラメータがある場合、等価な式は[7]
9) 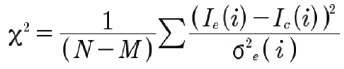
となる。
1標準偏差の不一致は上記の式の合計に1を加え、χ²の値が1であれば、2つの画像はノイズによって与えられる不確実性の範囲内で同一であることを意味する。N点からなる統計的に等価な画像の期待値は1であり、この値から1以上のランダムな偏差は起こりにくいと考えられる。
10) 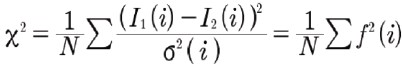
と書くことで、残差画像[10]の定義が導き出されます。
残差画像は、2つの画像間の(不)一致を視覚化し、定量化するために使用されます。残差画像の利点は、2つの画像の一致度を単一の数値で示すのではなく、局所的な適合度の2次元マッピングであることです。したがって、差分画像では不一致の大きい領域がより明確に示されます。最適な一致は、やはりχ²を最小化することによって定義されます。
フィッティングパラメータは画像のフーリエ変換にも適用でき、比較対象となるデータポイントの数が削減される場合があることに注意することが重要です[11]。欠陥のない結晶材料の画像の場合、フーリエ成分は格子のブラッグ反射に対応する周波数においてのみ非ゼロとなるが、これは厳密には、モチーフが多数の繰り返し領域にわたって平均化され、境界における不連続性による縞模様が除去されるように格子座標上に再サンプリングされた場合にのみ当てはまる。フーリエ係数の複素値は画像強度の代わりに用いられる。
興味深いことに、異なるマッチング基準を使用すると、最適化されたパラメータの値がわずかに異なる可能性がある[12]。
異なる平均値とコントラストレベルの調整
画像強度の絶対値は不明であり、実験画像と計算画像が線形関係にある場合があるため、画像強度を正規化する有用な方法は、平均値を減算し、標準偏差で割ることです。これにより、線形関係にある画像ではD2 = 0、無関係なデータでは約2になります。
同様に、相互相関係数は-1から1の範囲にあり、2つの画像が線形関係にある場合は極値を取り、無関係なデータでは0に近くなります。
もう1つの方法は、画像を同じ平均値にスケーリングすることです。これは次のように行われます。
11) 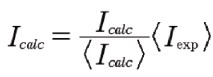
ここで、計算画像は実験画像の平均にスケーリングされます。
平均値、コントラスト、画像パターンが画像マッチング基準にどのように影響するかを理解するためには、二乗平均平方根差(Root Mean Squared Difference)を3つの項[13]にどのように分解できるかを考えることが有用です。
12) 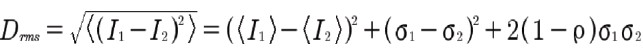
ここで
13) 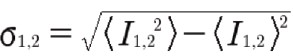
および
14) 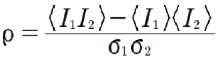
第1項は2つの画像の平均の差を表し、両方の画像が同じ平均値に正規化されている場合はゼロになります。第2項は2つの画像間のコントラストの差を表し、第3項(正規化相互相関係数と同じ)は2つの画像のパターンの差(類似性)を表します。
ただし、正規化相互相関係数はパターンの類似性のみを表し、コントラストの変動や平均レベルの差は無視することに注意することが重要です。一般的に、実験画像とコンピュータシミュレーション画像間の不一致のほとんどは、コントラストの差によることが分かっています[14]。コントラストの差は桁違いになることもあり、その原因は一般的に以下の要因に起因します。
- 位置ずれ
- 試料の振動
- 非弾性散乱
- 試料の損傷
しかしながら、計算によれば上記の要因だけではコントラストの差異を解消するには不十分であることが示されているため、コントラストの差異の性質については議論が続いています。考えられる説明としては、実験画像には考慮されていない一般的な背景が存在することが挙げられます。
マッチング基準へのノイズの影響
2つの画像が等しいと判断されるためには、ノイズと、画像を決定するパラメータによるマッチング基準の不確実性または誤差の影響を考慮する必要があります。
相互相関係数へのノイズの影響を研究した結果、ノイズが存在する場合、2つの画像I1とI2+h(ここでhは画像I2に重畳されたランダムノイズを表す)の相互相関係数CCFは、次のように表されることが明らかになりました[13]
15) 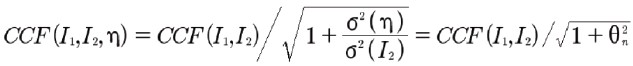
16) 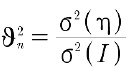
超角度への影響は、小角度近似にあります。
17) ![]()
2つの画像が、結像パラメータ(焦点ずれ、厚さなど)の1つに小さな誤差がある以外は同一である場合、角度の誤差はパラメータ誤差に比例します。独立したパラメータ誤差による角度の誤差は、
18) 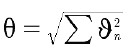
パラメータ誤差によるCCF(パターンマッチング)の典型的な不一致は、以下のとおりです。
| Parameter | Error | theta(mrad) |
|---|---|---|
| Noise(ノイズ) | 0.06 | |
| Composition(組成) | ±0.03 | 0.02 |
| Thickness(厚み) | ±2nm | 0.2 |
| Defocus(焦点ずれ) | ±15nm | 0.4 |
| Beam Tilt(ビーム傾斜) | <1.5mrad | 0.8 |
| Astigmatism(非点収差) | <15nm | 0.2 |
| Crystal Tilt(結晶傾斜) | <2mrad | 0.6 |
| Beam Diverg(ビーム発散) | <0.3mrad | 0.1 |
| Focal Spread(焦点広がり) | <5nm | 0.15 |
| Vibration(振動) | <0.04nm | 0.2 |
カイ二乗またはカイ二乗基準
上記の方法はすべて、2つの画像間の一致または不一致を測定しますが、重要な問題は、それらがどの程度一致するかではなく、系統的誤差と非系統的誤差を考慮した上で、どの程度一致するかです。したがって、フィッティングパラメータは、データの統計的性質と、データポイントの既知の精度を考慮する必要があります。
したがって、フィッティングパラメータは、最大尤度(確率)モデルに依存し、データポイントの確率分布がわかっている場合に、AがBに等しい確率の尺度となる必要があります。
相関のないノイズのガウス分布が存在する場合、各データポイントは、1つのピクセルのノイズが隣接するピクセルのノイズと相関しないガウス確率分布を持ちます。これは、χ²基準につながります。この基準は、調整可能なパラメータの数と各データポイントの誤差を考慮に入れます。
前述のように、期待値から1シグマ離れたデータポイントは、χ²の合計に1を加算します。
同様に、A = B と仮定した場合、測定される確率が1%しかないデータポイントは、χ² の合計に 6.63 という値を追加します。したがって、χ² の値が約 6 より大きい場合、A が B と等しい確率は 1% 未満であることを示します。
フィッティングパラメータは、統計的ノイズによるデータポイントの分布モデルに依存し、無相関ノイズのガウス分布が基準となります。しかし、画像内のノイズの統計的性質を判断することが重要です。これは、ノイズを除いて同等とみなされる多数の画像領域から決定されたノイズ分布を調べることで行うことができます。非ガウス分布の場合は、基準は修正されますが、それでも [7] に基づいています。
構造決定
「未知の」構造を決定するには、計算画像、出射波動関数、または回折パターンと実験データとの比較を行う必要があります。前述のように、この比較は、様々な一致/不一致基準を用いて行うことができます。
理想的には、構造の決定は、実験データと計算データ間の不一致が実験データの誤差範囲内に収まるまで構造を修正することによって行われます。原理的には、画像化パラメータ自体を原子座標と共に変化させることが許容されます。しかし、実際には、画像化パラメータは可能であれば個別に最適化されます。これにより、問題の複雑さが軽減され、一致基準を最適化する解の探索に必要なステップ数が削減されます。
「既知」の構造が存在するにもかかわらず未知の欠陥が存在する場合、画像化パラメータと試料の厚さは、まず既知の構造から決定されます。
未知の入力パラメータセットを決定するには、以下のものが必要です。
1) 実験データから得られた画像(実空間または逆格子空間)。
2) 1)と比較する画像を生成する計算手法。
3) 1) と 2) を比較する方法
4) 1) と 2) が統計的に同等である場合の、3) に基づく基準
5) 最終構成が 4) を満たすように最適化される、調整可能な入力パラメータの初期セット
6) 最終構成が有限時間内に見つかるように、調整可能なパラメータを変化させる方法
上記には重要な仮定が立てられており、それは、入力パラメータを正しく選択すれば、2) で使用される計算方法が 1) の画像を生成するというものです。これは別の問題であるため、ここでは取り上げません。この仮定の妥当性については議論の余地があり、計算方法にはさらなる改良が必要であることは認識されています。
しかしながら、以下では、この仮定は妥当であると仮定します。
像または出口波動関数のマッチング
計算と実験を比較するには、像または回折パターンを比較することができます。完全な構造の場合、比較するデータ点の数は構造のブラッグ反射の数によって決まるため、回折パターンを比較することが有益です[11]。しかし、欠陥構造の場合、欠陥を記述する情報はブラッグスポット間の散漫散乱に存在するため、像を比較する方が効率的です。この議論全体は実空間と逆空間の両方に関連しますが、ここでは実空間の像のみを参照します。
模擬熱アニーリング
模擬熱アニーリングは、多変数関数の大域的最小値を求める比較的新しい手法です[15]。このアルゴリズムは、パラメータ(x₁、x₂、x₃、….xn)を変化させ、システムの最適構成が最小エネルギー状態、すなわち基底状態となるように、システムにエネルギーを割り当てることに基づいています。また、システムには温度が割り当てられ、構成が変化するにつれて温度は徐々に低下していきます。初期配置 E₀(x₁,x₂,x₃,….xn) から、パラメータはランダムに変化し、各変化に対して新しいエネルギー Ej(x₁,x₂,x₃,….xn) が計算されます。ΔE = Ej(x₁,x₂,x₃,….xn) – Ej-1(x₁,x₂,x₃,….xn) < 0 の場合、新しい配置は常に受け入れられます。それ以外の場合、新しい配置が受け入れられる確率は P です。ここで、
19) 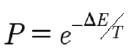
E と T は無次元量です。
各温度に対して、システムは一定回数の変化を経て、上記の基準に基づいて新しい配置を受け入れるか拒否するかを決定します。
指定された回数の遷移が成功すると、温度は一定量だけ下げられ、パラメータが再び変更されます。反復処理の関数として、システムのエネルギーは、期待される最小エネルギー構成に向かって減少し、指定された回数の試行でそれ以上の成功例が得られなくなるか、温度が下限に達すると、プロセスは終了します。
計算画像と実験画像を比較する場合、システムのエネルギーはc2、または画像の不一致を測定する他の量のいずれかに選択できます。相互相関係数に基づいて比較する場合、エネルギーは1-CCFとしてとらえることができます。
シミュレーテッド・サーマル・アニーリングは、局所的最小値に陥ることなく、大域的最小値を見つけるのに非常に強力であることが証明されている、単純な手法です。これは開始条件と開始温度の選択に敏感であり、ある程度の実験が必要になる場合があります。最小値付近では、勾配法に基づく探索手法よりも最適性が低くなる傾向があり、シミュレーテッドアニーリングアルゴリズムが終了した後は、別の探索アルゴリズムに切り替えることが代替手段となる場合があります。
シミュレーテッド進化
シミュレーテッド進化は、ダーウィンの「適者生存」の原理[16]をモデルにした、大域的最小値を求めるためのもう1つの手法です。まず、適合させるべきすべての変数の初期設定を行い、ランダムジェネレータ(突然変異ジェネレータ)を用いて初期設定から複数のセットlを生成します。このセットlは、子世代の第一世代を表します。アルゴリズムは以下のように進行します。
i) l個の子すべてについて、品質関数Q(適合度)を評価します。
ii) 次の世代の親となる生存者のサブセット(μ<l)を選択します。
iii) 親のパラメータベクトルの一部を選択して混合した後、ランダムジェネレータを適用して新しい世代を作成します。
iv) 以下のいずれかの基準を満たすまで、i) に戻る。a) 最大世代数に達した、または b) 臨界適合度に達した。
その他の手法
入力パラメータを変更することで、適合度に対する勾配が最大となる経路をシステムが進むように調整する他の方法もある[17]。それぞれの方法には利点がある。シミュレーテッド・サーマル・アニーリングとシミュレーテッド・エボリューションは、最適な適合度に近づくための優れた手法である。適合度が最小値に近づいたら、測定の不確かさの範囲内に収まるまで、勾配法を用いてさらに改良を進めることができる。
参考文献
- Völkl E. et al (1994) Density correction of photographic
material for further image processing in electron microscopy,
Ultramicroscopy 55, 75-89 - RuijterW.J. de andWeiss J.K. (1992) Methods to measure
properties of slow-scan CCD cameras for electron detection, Rev. Sci.
Insts. 63, 4314 - Mooney P.E. et al. (1993) MTF restoration with slow-scan CCD
cameras, Proc.Annual Meeting of the Microsc. Soc. of America 51, 262-
263 - RuijterW.J. de andWeiss J.K. (1993) Detection limits in
quantitative off-axis electron holography,Ultramicroscopy 50, 269-283 - Frank J. (1972) Two-dimensional correlation functions in electron
microscope image analysis, Electron Microscopy,the Institute of Physics,622 - SaxtonW.O. (1996) Pre-processing of data, registration,
distortions,resampling,noise removal, and noise estimation,
NCEM workshop on quantitative HRTEM,April 18-20,
NCEM/LBNL Berkeley CA, USA - Zhang H. et al (1995) , Structure of planar defects in
(Sr0.9Ca0.3)1.1CuO2 infinite-layer superconductors by
quantitative high-resolution electron microscopy,Ultramicroscopy
57, 103-111 - Smith A.R. and Eyring L. (1982) Calculation, display and
comparison of electron microscope images modeled and observed,
Ultramicroscopy 8, 65-78 - Press,W.H. et al (1986) Numerical Recipes,the art of
scientific computing. Cambridge University Press 1986 ISBN 0
521 30811 9, p. 502 - KingW.E. and Campbell G.H. (1994) Quantitative
HREM using non-linear least-squares methods,Ultramicroscopy
56, 46-53 - Thust A and Urban K. (1992) Quantitative high-speed
matching of high-resolution electron microscopy images,
Ultramicroscopy 45, 23 - Möbus G. and Rühle M. (1994) Structure determination of
metal-ceramic interfaces by numerical contrast evaluation of
HRTEM micrographs,Ultramicroscopy 56, 54-70 - Hÿtch M.J. and StobbsW.M. (1994) Quantitative criteria
for the matching of simulations with experimental images,
Microsc. Microanal. Microstruct. 5, 133-151 - Hÿtch M.J. and StobbsW.M. (1994) Quantitative
comparison of high resolution TEM images with image
simulations,Ultramicroscopy 53, 191-203 - Thust A., Lentzen M. and Urban K. (1994) Non-linear
reconstruction of the exit plane wave function from periodic highresolution
electron microscopy images,Ultramicroscopy 53, 101-120 - Möbus G. (1996) Retrieval of crystal defect structures from
HREM images by simulated evolution I. Basic technique,Ultramicroscopy
65, 205-216 - Press,W.H. et al (1986) Numerical Recipes,The art of scientific
computing. Cambridge University Press 1986 ISBN 0 521 30811 9, p. 521
14.高分解能電子顕微鏡における最適および準最適フィルター
1.はじめに
高分解能透過型電子顕微鏡(HRTEM)で記録される画像のほとんどには、自然酸化膜、汚染物質、支持膜などのアモルファス層の存在が見られます。アモルファス層は、対象となる結晶性材料から得られる情報を劣化させ、信号対雑音比を低下させます。この場合、信号とノイズと呼ばれるものは、実際には2つの信号であり、1つは試料の結晶領域から、もう1つはアモルファス層から生じます。
フィルム、イメージプレート、または低速走査CCDカメラに記録される信号は、電子と試料との相互作用によって決まり、原理的にはアモルファス領域と結晶領域の成分に分離することはできません。しかし、第一近似として、アモルファス材料の効果は、アモルファス材料の像を結晶性材料の像に加えることです。数学的には、これは弱位相物体近似(WPOA)の妥当性の範囲内でのみ示されます。薄い試料の場合、WPOA(Cowley & Moodie, 1957)を用いると、試料の出射面における電子波動関数は、
実空間(1)
または逆空間(2)
で表すことができます。
ここで、σは相互作用定数、tcとtaは結晶質と非晶質材料の厚さ、VcとVaはそれぞれ2つの投影されたポテンシャルです。
対物レンズが電子波動関数に及ぼす影響は、逆位相空間において位相係数Χ(u)を加えることです。この結果、記録された強度のフーリエ変換は、第一近似で、
(3)
対応する実空間表現は、
(4)
成分F(u)は複素数であり、像は実数であるため、F*(u) = F(-u)となります。
上記の式には、部分コヒーレンスの影響は含まれていません。部分コヒーレンスでは、記録された像は、エネルギーと入射方向の広がりを持つ電子からの非コヒーレント像の和となります。しかし、部分コヒーレンスを考慮しても、記録信号が結晶成分とアモルファス成分の2つの成分に分解されることは変わりません。ただし、画像形成において非線形項が無視される限りです(O’Keefe 1979)。弱位相物体近似は通常、アモルファス層に対して有効であり、アモルファス層が画質に大きな影響を与える厚さの結晶に対しても多くの場合適用できます。
2つの信号は周波数領域において明確に異なる特性を示します。非晶質成分は逆格子空間に広がり、その振幅は逆格子ベクトルの大きさに依存し、ランダムな変動を除いて方位角とは無関係とみなせます。結晶性物質からの信号は、原子面間の間隔に対応する特定の空間周波数付近でピークを示します。実空間の情報は分離不可能である一方、2つの信号は周波数領域においてかなりの程度まで分離可能であります。
本論文の目的は、記録信号I(r)のフーリエ変換から得られるF(u)から信号Fc(u)を推定し、非晶質物質が存在しない場合の記録像Ic(r)の推定値を得るための自動手順を概説することです。
2.フィルタの数学的導出
2.1. 最適フィルタ(ウィーナーフィルタ)
信号 Fc(u) の推定値は次のように表されます。
(5) ![]()
ここで、真の信号 Fc(u) と推定値 Fest(u) の二乗和が最小となるように解を最適化します。これは、次の量を最小化することで表されます。
(6) 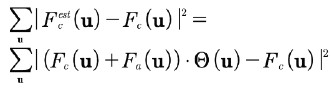
上記の式は、各項を最小化することで最小化されます。
について微分をゼロとすると、次の式が得られます。
(7) 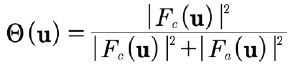
上記のフィルタはよく知られており、ウィーナーフィルタと呼ばれています (Rabiner & Gold, 1975)。ウィーナーフィルターの導出において、Fc(u)とFa(u)は無相関として扱われることに注意することが重要です。したがって、結晶質材料と非晶質材料からの信号の間には相関がないという基本的な仮定があります。2つの信号の推定値間の相関の程度は、非晶質部分と結晶質部分の厚さに依存して変化しますが(Hÿtch & Chevalier, 1994)、第一近似では無視できると考えられます。ウィーナーフィルターとその変種(キャノンフィルター(Cannon, 1977)を含む)、およびそれらのHREMでの使用については、Marks(Marks, 1996)によって詳細に議論されています。
Θ(u) を決定するには、|Fc(u)|² と |Fa(u)|² の両方の推定値が必要です。
「最適フィルタは最小化問題から得られるため、最適フィルタを適用して得られる結果の品質は、真の最適値と、フィルタが決定される精度の2乗程度しか違わない」(Press et al., 1986)。したがって、フィルタのかなり粗い推定値でも優れた結果が得られることが多いのです。
(8) ![]()
と書くと、最適フィルタの推定値として
(9) 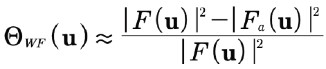
が得られるので、記録された信号のフーリエ変換と合わせて決定する必要がある唯一の量は |Fa(u)|² です。第3節では、|F(u)|² から |Fa(u)|² を決定する方法について説明します。
2.2. 平均背景減算フィルタ (ABSF)
(10) 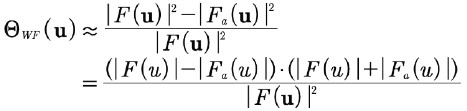
ウィーナーフィルタを次のように近似すると、
(11) 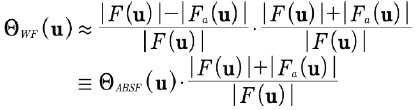
(12) 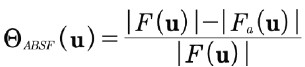
2つのフィルタの関係は次のようになります。
2つのフィルタの漸近的な挙動は同じで、
(13) 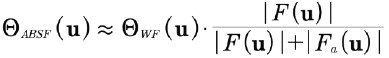
F(u) >> Fa(u) の場合には、フィルタはほぼ等しくなります。背景減算フィルタは、中間領域ではやや強いフィルタリング効果をもたらしますが、第4節に示す例からわかるように、2つのフィルタは同等の結果をもたらします。
上記において、フィルターΘabsf(u)はフィルターΘwf(u)から導出されています。実際、フィルターΘabsf(u)の歴史的背景は、ウィーナーフィルターとの関係が理解される以前からNCEMで導入され、長年使用されていたことです。
背景減算フィルターは、ソフトウェアパッケージDigital Micrograph(Gatan, Inc.)のNCEM画像処理拡張機能(Kilaas & Paciornik, 1995)に組み込まれています。ABSFフィルターは、同名の別のフィルター(Sattler & O’Keefe, 1987)と混同しないでください。後者は主観的なフィルターであり、ユーザーは結晶材料に関連する反射を識別し、強いピークを、位相がランダムで、振幅がピーク近傍の領域から取得されたフーリエ成分に置き換えることで背景を構築する必要があります。
平均背景減算フィルタは、その名の由来となっている単純な幾何学的記述を持っています。信号の結果を次のように書き表すと、
(14) 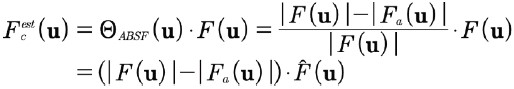
得られたフーリエ成分のベクトル表現は、記録された信号のフーリエ成分から、信号Fa(u)の推定振幅によって長さが与えられる同じ方向のベクトルを差し引くことで得られる。これは図1に示されている。
3.背景の推定
非晶質背景からの信号は、逆格子空間に広がり、その振幅は動径周波数|u|に依存し、ランダムな変動を除いて方向には依存しません。したがって、振幅|Fa(u)|を推定するには、与えられた動径周波数|u|に対する平均フーリエ振幅を求め、原理的には信号Fc(|u|)からの寄与を排除する必要があります。しかし、信号Fc(u)は逆格子空間に局在しており、中心から数ピクセル以上離れた任意の半径|u|に対して、Fc(u)は曲線|u| = 定数に沿った限られた数のサンプリング点にのみ対応します。さらに、信号Fc(u)は通常Fa(u)よりもはるかに大きく、その大きさに基づいてFa(u)と区別できる場合がよくあります。フィルターを適用して得られる結果は、背景信号の平均の計算方法にあまり左右されないことが判明しました。円全体 |u| = 定数で平均化して背景信号を推定すると、円に沿って結晶ピークが存在する場合、背景の推定振幅が実際の値よりも高くなるにもかかわらず、多くの場合良好な結果が得られます。しかし、振幅のヒストグラムから背景をより適切に推定できます。ヒストグラムは、背景信号を大きな結晶の寄与から分離し、ピクセル値の大部分は非晶質材料による背景信号に由来します。
したがって、平均振幅 |Fa(|u| = 定数)| は、円 |u| = 定数に沿った振幅のヒストグラムを決定し、信号 Fa(u) からの寄与を減少させる外れ値を除外してヒストグラムの平均を計算することで推定できます。結晶ピークが存在する場合の|u|=定数のフーリエ振幅の典型的なヒストグラムを図2に示す。この場合、結晶性物質に対応するピクセル数は比較的少なく、ヒストグラム分布は二峰性となり、ピクセルの大部分は下側のピーククラスターに寄与している。
平均背景信号は半径ごとに計算され、|Fa(u)|²の推定値が導出される。次に、|Fc(u)|²が
(15) ![]()
式から推定され、フィルタΘwf(u)とΘabsf(u)が計算される。
4.適用例
2つのフィルターの効果を示し比較するために、ゼオライトのHRTEM像に適用しました。ゼオライトは電子ビーム下で非常に急速に損傷を受けるため、非晶質になる前の結晶相から像を取得することは困難です。図3は実験的なHRTEM像、図4は対応するフーリエ変換を示しています。結晶信号は、放射周波数|u|に応じて変化する背景に対して鋭いピークとして明瞭に確認できます。コンピュータは、周波数領域における強度の変化を自動的に解析し、推定された背景を決定します。図5は、放射周波数|u|の関数として推定された背景強度を示しています。低周波数では、背景は非常に少ないデータ点から推定されるため、ランダムな変動に対して非常に敏感になります。一部の周波数では、結晶性信号が推定バックグラウンドにわずかに寄与しているように見えますが、推定バックグラウンドにおけるそれに伴う誤差は、フィルターの機能にほとんど影響を与えません。結晶性物質に起因する実際のピーク強度は、通常、バックグラウンド強度よりも1~2桁大きくなります。
バックグラウンドが推定された後、コンピュータは自動的にフィルターΘwf(u) またはΘabsf(u) を構築します。図4に示すように、元のデータのフーリエ変換にフィルターΘwf(u) とΘabsf(u) を適用することで、非晶質物質に起因する信号成分が低減されます。
図6と図7は、それぞれフィルターΘwf(u)とΘabsf(u)が元データのフーリエ変換に及ぼす影響を示しています。逆フーリエ変換によって得られた対応する画像を図8と図9に示します。図8と図9に示された画像は、結晶部分によって生成された信号の推定値に過ぎず、真の信号として解釈すべきではありません。画像の結晶領域はノイズが少なく、個々のユニットセルによって生成された画像を識別しやすくなっています。
また、フィルタリングされた画像は結晶性物質の形状を保存しているように見え、画像を注意深く観察すると、未処理画像では識別できない特徴がフィルタリングされた画像には存在しないことがわかります。
ゼオライト構造単位を示す領域を見つけるのは、元データよりもフィルタリングされた画像から始める方がはるかに簡単です。構造単位を含む領域を抽出することで、テンプレートとフィルタリングされた画像との間の相互相関係数を、画像に対するテンプレートのあらゆる位置について計算することができます(Paciornik et al., 1996)。
これにより、-1から+1の範囲の値を持つ新しい画像が得られ、値が1に近いほどテンプレートに類似した領域であることを意味します。図10は、テンプレートが挿入された相互相関画像を示しています。これらの位置を使用して、元のデータから領域を抽出し、単位セルの平均画像を取得できます。平均テンプレートを図11aに示します。比較のために、ウィーナーフィルタリングされた画像から得られた平均テンプレートを図11bに示します。
5.議論
多くの人は、同じ領域の連続画像を平均化し、ノイズのみの変化を確実にすることだけが安全に実行できる処理だと主張するでしょう。なぜなら、同じ顕微鏡写真から類似領域を平均化することでさえ、系統的な構造的変動や画像パラメータの系統的誤差によって引き起こされるアーティファクトが生じる可能性があるからです。
どのような種類のフィルタリングでも、フィルタリングされた画像がもはや生のデータを意味のある形で表現しなくなる危険性があります。
しかし、記録された信号の性質と撮像条件に関して賢明な推測を行い、それに従って処理を進めることが多々あります。本研究の基本的な仮定は、記録された画像のフーリエ変換は、2つの相関のない信号の和として扱えるというものです。どちらの記述も厳密には正しくありませんが、出発点として、第一近似が成り立つと仮定します。2つのフィルターを適用して得られた結果は、実際のデータと比較し、明らかなアーティファクトがないことを確認する必要があります。
結晶構造が非結晶領域にまで広がるなどの明らかなアーティファクトは、フィルターが不適切であることを示しており、多くの場合、ノイズを過大評価した結果、フィルタリングが過剰になったことが原因です。実験画像の場合、信号(「結晶画像」)は未知であるため、フィルターが実験データに与える影響を定量的に評価することは困難です。
しかし、既知の結晶性物質と既知のノイズを用いたシミュレーションデータの場合、結果を定量的に比較することができます。テストでは、画像のサイズとノイズ推定値と真のノイズとの関係に応じて、信号対雑音比の改善は3~7の範囲にあることが示されています(Marks, 1996)。ウィーナーフィルタと平均背景減算フィルタはどちらも、ランダム変動を除けば信号は動径周波数|u|のみで変化すると仮定し、非晶質背景による信号のパワースペクトルを推定することで、データから自動的に作成されます。
ウィーナーフィルタは、最小二乗法で信号Fc(u)の最適な推定値を与えます。背景減算フィルタは、「信号」(Fc(u))と「ノイズ」(Fa(u))の振幅が同程度である周波数でわずかに強い減衰をもたらしますが、それ以外はウィーナーフィルタと非常によく似た結果をもたらします。両方のフィルターが利用可能であることを考えると、バックグラウンド減算フィルターよりもウィーナーフィルターを選択すべきであることは明らかです。
しかし、バックグラウンド減算フィルターは長年にわたり多くの科学者によって使用されているため、その適用性とウィーナーフィルターとの関係に関する情報を提供することが重要です。どちらのフィルターも自動的に動作します。ユーザーには選択肢が提示されず、アルゴリズムに組み込まれているもの以外の仮定も行われません。適切に適用されれば、結晶性物質とアモルファス層が組み合わさったHRTEM像から有用な情報を抽出するのに役立つ可能性があります。
謝辞
本研究は、米国エネルギー省エネルギー研究局基礎エネルギー科学部材料科学課長(契約番号 DE-AC03-76SF00098)の支援を受けて実施されました。
参考文献
Cannon,T.M. (1977) Digital Image Deblurring by Nonlinear
Homomorphic Filtering, Ph.Dthesis, Computer Science Department,
University of Utah, Salt Lake City,UT
Cowley, J.M.& Moodie, A.F. (1957)The Scattering of Electrons by
Atoms and Crystals. I.A NewTheoretical Approach,Acta Cryst., 10, 609-
619
Gatan, Inc, 6678 Owens Drive, Pleasanton,CA 94588, USA.
Hÿtch, M.J, and Chevalier, J.P. (1994)The effect of Amorphous Surface
Layers on HREM Images of Crystalline Material, Proceedings of ICEM,
Paris, 367-368
Kilaas, R.& Paciornik, S. (1995)The NCEM public domain
software library of extensions to Digital Micrograph. Proc. of MSA
46, 628-629
Marks, L.D. (1996)Wiener-filter enhancement of noisy HREM
images,Ultramicroscopy 62, 43-52
O’Keefe, M.A. (1979) Resolution-damping functions in non-linear
images, Proc. of EMSA 37, 556-557
Paciornik, S., Kilaas, R., Turner, J., Dahmen, U. (1996) A
Pattern Recognition Technique for the Analysis of Grain
Boundary Structure by HREM.Ultramicroscopy, 62, 15-27
Press,W.H. et al (1986) Numerical Recipies,The art of scientific
computing. Cambridge University Press 1986 ISBN 0 521 30811
9, p. 419
Rabiner, L.R.& Gold, B. (1975),Theory and application of
digital signal processing Englewood Cliffs, N.J.: Prentice-Hall
Sattler, M.L. and O’Keefe, M.A. (1987) Atomic Structure Analysis
of Small Particles Supported on Amorphous Material, Proc. of
EMSA 45, 104-105
15.図
図1 記録信号のフーリエ成分F(u)は、成分Fa(u)とFc(u)の和として表されています。フィルタΘABSF(u)を用いて所望の信号Fc(u)を推定すると、Fcest(u)が得られます。
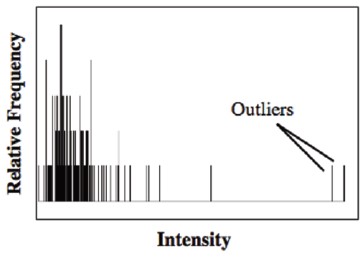
図2. 周波数空間における円に沿った振幅のヒストグラム。|
u| = 定数。ほとんどのピクセル値は背景信号に関連付けられており、ヒストグラムの左側のピーク群に寄与しています。右端に位置するピークは結晶材料から発生する信号に関連付けられており、平均背景振幅を推定する際に背景から簡単に分離できます。

図3. 電子線によって急速に損傷を受けているゼオライトの実験画像。中央部はまだ結晶状態にある部分を示している。非晶質の「ノイズ」が大量に存在するため、結晶領域から有意義なデータを得ることは困難である。

図4 図3に示す画像のフーリエ変換。
画像の結晶領域は局所的な鋭いピークに寄与し、非晶質材料はぼやけた背景に寄与しています。

図5. 図4に示したフーリエ変換から得られた、放射周波数|u|の関数としての推定背景強度。

図6. 元のデータのフーリエ変換にウィーナーフィルタを適用した結果。未処理のデータと比較して背景が低減されています。

図7. 元データのフーリエ変換に背景減算フィルタを適用した結果。

図8. ウィーナーフィルタを用いて得られたデータを逆フーリエ変換した結果画像

図9. 背景減算フィルタを用いて得られたデータを逆フーリエ変換して得られた画像。

図10. ゼオライトユニットセルの画像を含むテンプレートとウィーナーフィルタを適用した画像との間の相互相関係数を示す画像。
テンプレートはフィルタを適用した画像から抽出されている。十字はテンプレート画像と類似する領域の位置を示している。

