SigmaPlot 基本操作ガイド – ANOVA
SigmaPlot による対応のある 2 標本の t 検定に関する使用例を説明いたします。
SigmaPlot には、次の ANOVA の検定手法が用意されています。
- One Way ANOVA
3つ以上のグループの母平均に統計的な差があるかどうかを検定 - Two Way ANOVA
2つの要因を持つ独立したグループ間の母平均の差を検定し、各々の因子の主効果や交互作用を評価 - Three Way ANOVA
3つの要因を持つ独立したグループ間の母平均の差を検定し、各々の因子の主効果や交互作用を評価 - One Way Repeated Measures ANOVA
同じ被験者 (対象) に対して複数回測定したデータにおける母平均の差を検定 - Two Way Repeated Measures ANOVA
同じ被験者 (対象) に対して複数回測定したデータにおいて、2つの要因の主効果や交互作用を含む母平均の差を検定
One Way ANOVA とは
One Way ANOVA は、例えば 3 つの異なるグループ (A, B, C) がある場合に、これらのグループ間に差があるかどうかを調べるときに使用します。比較するデータは、以下の条件を満たしている必要があります。
- 正規性を満たす (各グループ内のデータが正規分布に従う)
- 等分散性を満たす(各グループの分散が等しい)
例題
次の例題について、SigmaPlot を用いたOne Way ANOVA (一元配置分散分析) の実施手順を紹介します。
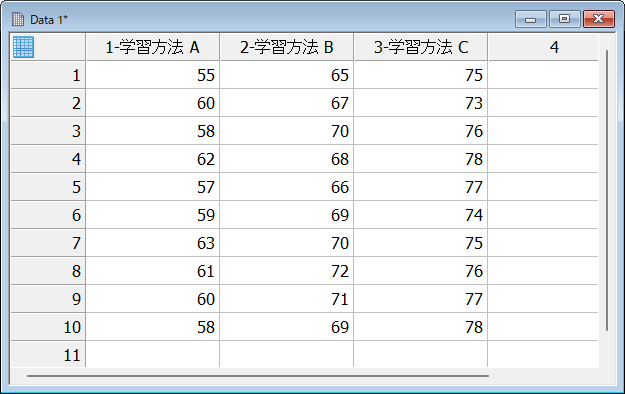
学習法による試験の成績を比較したいと思います。A、B、C の学習法で10名ずつの点数の結果です。この 3つの学習法に、有意な差があるかどうかを One Way ANOVA で検定します。
| 学習方法 A | 学習方法 B | 学習方法 C |
| 55 | 65 | 75 |
| 60 | 67 | 73 |
| 58 | 70 | 76 |
| 62 | 68 | 78 |
| 57 | 66 | 77 |
| 59 | 69 | 74 |
| 63 | 70 | 75 |
| 61 | 72 | 76 |
| 60 | 71 | 77 |
| 58 | 69 | 78 |

操作手順
SigmaPlot の Σ メニューをクリックして New → Notebook を実行しワークシート (Data 1) を表示します。
下図のようにワークシートにデータを入力します。
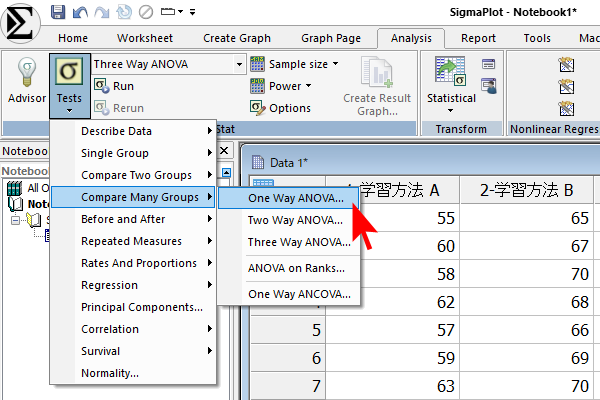
続いて Analysis タブ→ Tests → Compare Many Groups → One Way ANOVA… を実行します。
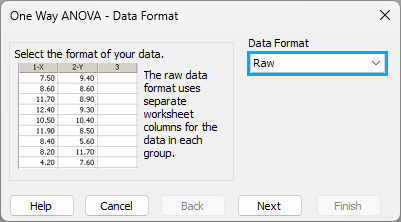
Raw 形式のまま、Next ボタンをクリックします。
ワークシートから A、B、C の学習方法の変数をマウス操作で選択 (もしくは Data for Data プルダウンメニューから3つの学習方法の変数を選択) して Finish ボタンを押します。
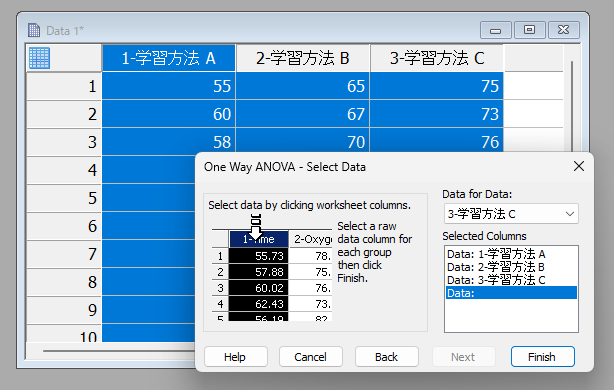
Multiple Comparison Options パネルが表示されます。ここでは、多重比較検定 (Post Hoc Test) の選択を行います。多重比較検定によりどの群とどの群に差があるかを調べます。
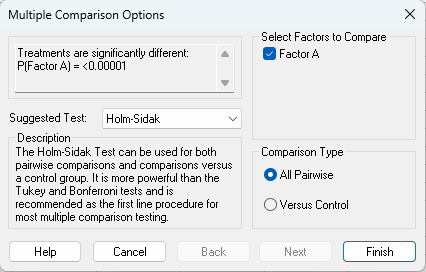
Holm-Sidak 検定が推奨されていますが、ここでは標準的な Tukey を選択して Finish ボタンを押します。
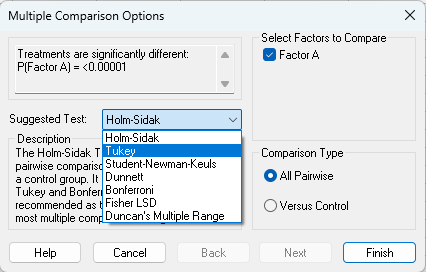
One Way ANOVA のレポートが表示されます。
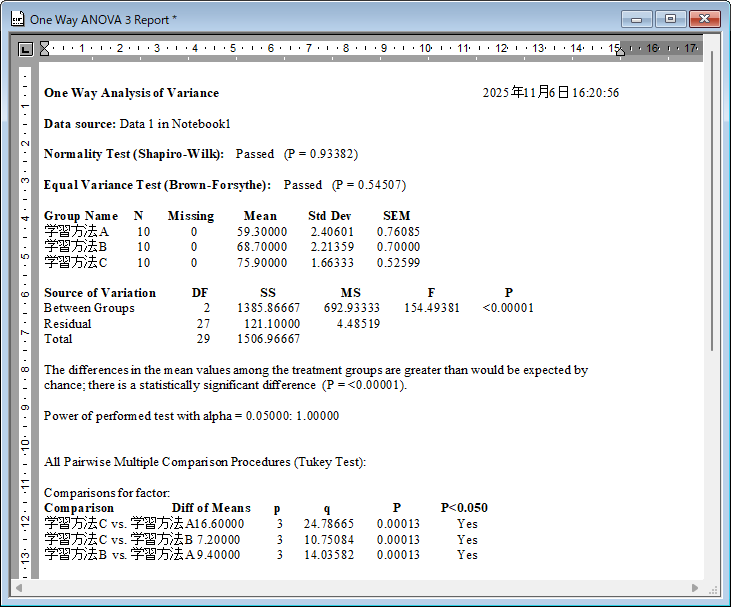
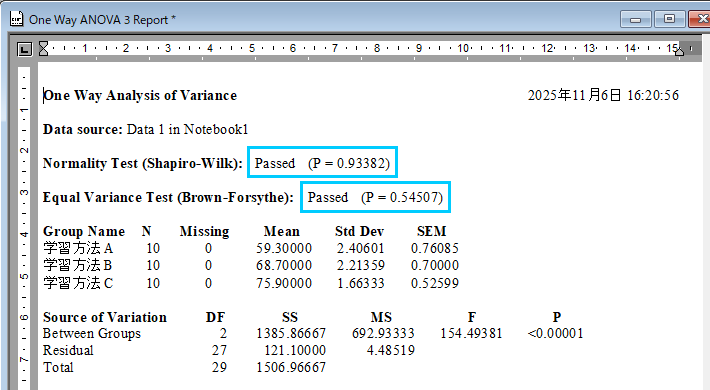
データが前提条件を満たしているか否かは、次の2つの検定結果から判断します。
正規性の検定 (Shapiro-Wilk)
- 帰無仮説: データは正規分布に従う
- 対立仮説: データは正規分布に従わない
等分散性の検定 (Brown-Forsythe)
- 帰無仮説: 2 つの分散は等しい
- 対立仮説: 2 つの分散は等しくない
有意水準 (帰無仮説を棄却するかを判断する基準となる確率) は α=0.05 としています。
正規性の検定 (Shapiro-Wilk) 及び等分散性の検定 (Brown-Forsythe) は、いずれも「Passed」と表示されています。P 値は有意水準 0.05 より大きく帰無仮説は棄却されず、2つの標本は正規性ならびに等分散性を満たしていると言えます。
データが正規性もしくは等分散性を満たしていない場合は、SigmaPlot のアドバイザー機能によりノンパラメトリック検定である Kruskal-Wallis One Way Analysis of Variance on Ranks の実施を促されます。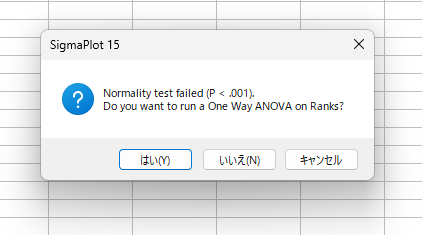
|
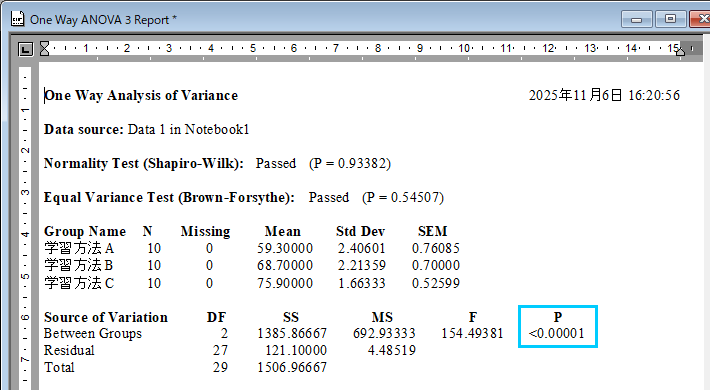
次に ANOVA の結果を確認します。ANOVA の帰無仮説と対立仮説は次のとおりです。
| 帰無仮説 H0 : μ1 = μ2 = μ3 すべての母平均は等しい 対立仮説 H1 : 少なくとも1つの母平均は他と異なる |
Source of Variation の内容は、群間 (Between Groups) の P 値が <0.00001 と α=0.05 より小さい値で帰無仮説は棄却され、対立仮説が採択されます。3つの学習方法には違いがあると言えます。
3つの学習方法に違いがあることがわかりましたので、どの学習方法とどの学習方法が異なるのかを Tukey の検定の結果を確認いたします。
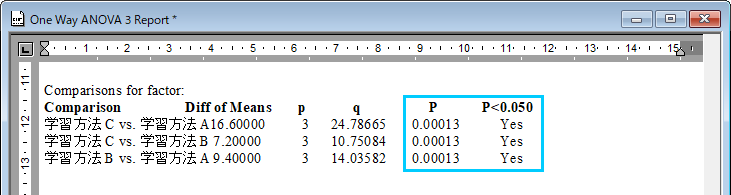
個々の学習法の比較において、すべての比較で P 値が 0.00013 です。α=0.05 より小さい値で帰無仮説が棄却され、対立仮説が採択されます。すべての学習法の組み合わせについて差があると言えます。
【レポートに表示されるANOVAの統計量】
● DF: (Degrees of Freedom) 自由度
● SS: (Sum of Squares) 平方和
● MS: (Mean Squares) 平均平方
群間の平均平方は次式であらわされます
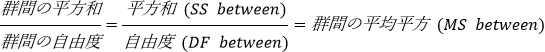
群内の平均平方 (誤差または残差平均平方とも言う) は次式であらわされます
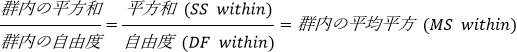
● F: F 統計量は次の比であらわされます
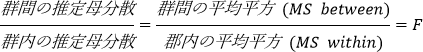
F 比が 1 に近い場合、群間に有意な差はないと言えます。(例: データグループは、すべてのサンプルが同じ母集団から抽出されたという帰無仮説と一致)。 F 値が大きい場合、少なくとも1つの標本が異なる母集団から抽出されたと言えます(例: ばらつきが、母集団におけるランダムなばらつきから期待されるよりも大きい場合など)。どのグループが異なるかを正確に判断するには、多重比較の結果を調べます。
● P: P 値 (有意水準) は、「グループ間に実際に差がある」と結論づける際に誤る確率、 つまり帰無仮説を誤って棄却する確率 (第一種の過誤:Type I error) を示します。 ANOVA では、F 統計量に基づいてこの確率を求めます。 P 値が小さいほど、「得られたデータが、帰無仮説(平均に差はない)では説明しにくい」ことを意味し、したがって「異なる母集団から得られたサンプルである可能性が高い」と考えられます。一般的に、P < 0.05 のとき「統計的に有意な差がある」と判断します。
【SigmaPlot がサポートする多重比較検定の各手法】
Holm-Sidak
- 分散分析で有意差が認められた場合に使用可能。
- 各群が等分散で正規分布に従っていると仮定して検定。
- 各群のデータ数が同じでなくても使用可能。
逐次的に有意水準を調整して多重比較による誤差(Familywise Error Rate)を制御する方法であり、Bonferroni法よりも検出力が高い。
Tukey
- 分散分析で有意差が認められなくても使用可能。
- 各群が等分散で正規分布に従っていると仮定して検定。
- 各群のデータ数が同じでなくても使用可能。
Student-Newman-Keuls
- 分散分析で有意差が認められた場合に使用可能。
- 各群が等分散で正規分布に従っていると仮定して検定。
- 各群のデータ数が同じである必要がある。
ステップワイズ法による優れた手法ですが、全体の危険率は指定した有意水準を上回るため単独での検定方法として使用すべきではない。
Dunnett
- 分散分析で有意差が認められなくても使用可能。
- 各群が等分散で正規分布に従っていなくても検定可能。
- 各群のデータ数が同じでなくても使用可能。
- 対照群として指定した1群と他の群を比較する方法。
比較数が少ないため他の多重比較検定に比べてより小さな差でも有意になる傾向がある。
Bonferroni
- 分散分析で有意差が認められなくても使用可能。
- 各群が等分散で正規分布に従っていると仮定して検定。
- 各群のデータ数が同じでなくても使用可能。
多重比較検定としてほとんどの場合に使用できるが、検出力はやや劣る。
Fisher LSD
- 分散分析で有意差が認められた場合に使用可能。
- 各群のデータ数が同じである必要がある。
- 各群が等分散で正規分布に従っていると仮定して検定。
指定した有意水準を一組の比較あたりの比較に用いるため検出力は優れるが、4群以上の検定では多重比較全体としての危険率が指定した有意水準を超えてしまうため使用すべきではない。
Duncan’s Multiple Range
- 分散分析で有意差が認められなくても使用可能。
- 各群が等分散で正規分布に従っていると仮定して検定。
- 各群のデータ数が同じでなくても使用可能。
Tukey法に比べて有意差が出やすく、第一種の過誤(誤って差があると判断する誤り)が増える傾向がある。探索的な比較に適している。
