3. 一般的な事項
このページでは、QTCAD の使用に関する一般的な事項について議論します。
3.1 単位
QTCAD では、デフォルトで SI 単位系が使用されます。例えば、距離はメートル、質量はキログラム、エネルギーはジュールで表現されます。
単位を明確にするために、それぞれのソルバーを説明しているセクション(理論 – 有限要素(半導体)や理論(超伝導体))では QTCAD API で単位を指定するのに使用する関連するオブジェクト属性の表を用意しています。
3.2 要素、ローカルノード、グローバルノード
QTCAD シミュレーションに必要な量を扱うのに、要素、ローカルノード、グローバルノードを区別することが重要です。
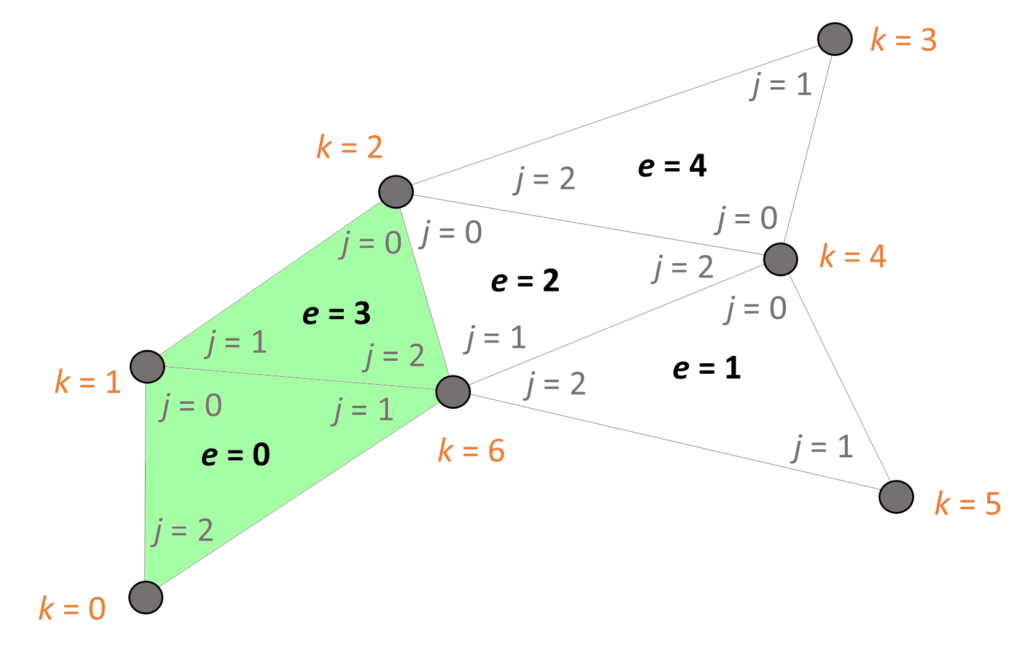
より良い理解のために例を用意しました。Fig. 3.2.1 は二次元の簡単なメッシュを示しています。
このメッシュには、\(e\) でラベル付けされた要素がいくつか存在します。そして、三角形に対応する一次のラグランジュ要素があります。それぞれの要素には \(j\) でラベル付けされたローカルノードがいくつか存在します。それぞれのローカルノードは \((e,j)\) の組み合わせでユニークに区別できます。加えて、これらのノードは単一のグローバルノード \(k\) を使ってもラベル付けできます。
ローカルノードとグローバルノードの区別はマテリアルの界面が不連続のとき有用です。このような場合には、同じグローバルノードに対応する二つのローカルノードに異なる値が与えられます。例えば、Fig. 3.2.1 の要素 \(2\) と \(3\) の界面では、グローバルノードが同じにもかかわらず、ローカルノード \((3,0)\) と \((3,2)\) には \((2,0)\) と \((2,1)\) と異なるパラメータが割り当てられます。
3.3. パラメータと変数
QTCAD で解く偏微分方程式 (PDE) では、パラメータと変数は区別されます。
パラメータは解かれる PDE の中で既知の量です。逆に、変数は未知の量で、微分方程式によって解かれます。例えば、ポアソン方程式では、
\(\nabla\cdot\left(\varepsilon\nabla\varphi\right)=-\rho,\)
誘電率 \(\varepsilon\) および 電荷密度 \(\rho\) はパラメータで、静電ポテンシャル \(\varphi\) は注目している変数です。
この区別は過度に形式的に見えますが、QTCAD ではパラメータと変数は別のデータ構造として扱われます。
パラメータは 1D もしくは 2D 配列として保存されます。1D 配列の場合、各エントリにはメッシュ要素にパラメータ値が含まれます。これはすべての要素でパラメータが一定であることを仮定しています。例えば、パラメータがマテリアルの種類によってのみ決定される場合です。2D 配列の場合、各エントリは要素の特定のローカルノードにあるパラメータ値に対応します。この場合、行は要素を参照し、列は要素内のローカルノードを参照します。
逆に、変数はメッシュのグローバルノードに保存されます。これは、QTCAD が各グローバルノードに解を持つ有限要素法を使用しているためです。
理論(有限要素(半導体))および理論(超伝導体)では、各種PDE に関連するパラメータと変数は明確に区別されています。
3.3.1. パラメータセッター
一般に、パラメータ値はデバイスの各領域のマテリアルを指定した際に自動的に各要素もしくはローカルノードに割り当てられます。しかし、特定の状況では、パラメータ値を手動で修正するのが便利です。このような操作を行うにはセッター、すなわち、パラメータ値を修正するために設計されたデバイスクラスのメソッドを使用します。各デバイスの適切なセッターは関連する理論セクション(スピン量子ビットおよび超電導量子ビット)で表になっています。
パラメータが空間の関数ならば、それを指定する方法が4つあります。架空のパラメータ param を考えると、デバイス dvc の対応するセッターを呼び出すには以下の操作を行います。
dvc.set_param(values, region=region)
パラメータ値を設定するには4つの方法が存在します。
1. グローバルノードを使用する。この場合、region は None(デフォルト値)、values は 1D 配列とし、デバイスメッシュの各グローバルノードにパラメータ値設定します。
x, y, z = dvc.mesh.glob_nodes.T
values = 0.5*x**2 + 2.5*y**2 + 3.0*z**2
dvc.set_param(values)
2. ローカルノードを使用する。この場合、region は None(デフォルト値)、values は 2D 配列とし、デバイスメッシュの各ローカルノードにパラメータ値設定します。配列の中身は、行は要素、列は各要素のローカルノードに対応します。
x, y, z = dvc.mesh.loc_node_coords()
values = 0.5*x**2 + 2.5*y**2 + 3.0*z**2
dvc.set_param(values)
3. 位置の関数を使用する。この場合、region は None(デフォルト値)、values はカーテシアン座標 \(x\), \(y\), \(z\) の呼び出し可能な関数とします。関数はすべてのグローバルノードの座標値を与える 1D 配列 \(x\), \(y\), \(z\) と互換性がある必要があります。
def my_func(x,y,z):
return 0.5*x**2 + 2.5*y**2 + 3.0*z**2
dvc.set_param(my_func)
4. 領域を使用する。この場合、region は物理的な領域のラベル文字列で、values はその領域全体で一定なパラメータ値です。
dvc.set_param(1.0, region="region_label")
手法1、2はメッシュが最適化されたときにデバイスパラメータを更新できないため、アダプティブメッシュでは機能しません。アダプティブメッシュを使用する際は手法3、4をお勧めします。
3.4. 有限要素
有限要素法では、物理量は形状関数によって離散化されます。形状関数は \(\phi_j^e(\mathbf{r})\) で示される空間の実関数で、\(e\) および \(j\) はそれぞれ要素、ローカルノードのインデックスで、\(\mathbf{r}\) は位置ベクトルです。形状関数は以下の性質を持ちます。
\(\phi_i^e(\mathbf{r}_j^e)=\delta_{ij},\)
ここで、\(r_j^e\) はローカルノード \((e,j)\) の位置で、\(\delta_{ij}\) はクロネッカーのデルタ関数です。位置の関数は有限要素の形状関数で以下のように展開されます。
\(f(\mathbf{r})\approx \sum_j \phi_j^e(\mathbf r)f_j^e ,\)
ここで、\(f_j^e\equiv f(\mathbf r_j^e)\) で、\(\mathbf r\) は要素 \(e\) の内側にあることを仮定しています。
QTCAD は1D, 2D, 3D で一次、二次のラグランジュ要素をサポートしています。これらの要素は 1D では線、2D では三角形、3D では四面体に対応します。\(n\) 次で \(d\) 次元の形状関数は \(d\) 次元で \(n\) 次の多項式です。要素当たりのローカルノードの数は多項式の未知数の数で決まるため、それは次元と次数に依存します。以下の表は QTCAD でサポートされている要素の種類に対するローカルノードの数を示しています。
| 次元 | 一次 | 二次 |
| 1D | 2ノード | 3ノード |
| 2D | 3ノード | 6ノード |
| 3D | 4ノード | 10ノード |
デフォルトでは、メッシュを生成したとき、Gmsh は一次のラグランジュ要素を仮定します。
二次の要素と対応するメッシュは以下の .geo スクリプトで生成されます。
Mesh 1;
Mesh 2;
Mesh 3;
Mesh.SecondOrderLinear=1;
SetOrder 2;
Save "mesh_name.msh";
コマンド SetOrder 2 によって一次から二次の要素に変換され、コマンド Mesh.SecondOrderLinear=1 で二次要素のすべてのローカルノードがラグランジュ線、三角形、四面体の内部にあることを保証します。これは、円形の境界では当てはまらない可能性があります。
一般に、QTCAD では簡単なため一次のメッシュでシミュレーションを行いますが、二次メッシュは、特にシュレーディンガーソルバーの場合に、同じ計算資源でより良い精度が得られる場合があります。
