2. QTCAD シミュレーションのワークフロー

このセクションでは、QTCAD デバイスシミュレーターを使った TCAD シミュレーションの基本的なワークフローを説明します。始めに QTCAD シミュレーションの主なステップをまとめました。次に、現在 QTCAD でサポートされている2つの構造作成ツールについて説明します。一つ目は devicegen で、デバイスレイアウトから平面構造を作成できます。2つ目は Gmsh で、任意の1D, 2D, 3D構造を作成できます。

2.1 QTCADシミュレーション

QTCADシミュレーションは以下の3つのステップに分けられます。

構造の決定とメッシング
物理問題の指定と解法
後処理

このセクションでは始めに2つの主要なワークフロー（Gmsh ワークフローと devicegen ワークフロー）を検討することで QTCAD シミュレーションの3つすべてのステップを網羅します。例として、ナノワイヤーデバイスとゲート量子ドットを考察します。

2.1.1. 例1：ナノワイヤーデバイス

このセクションの最初の例として、以下のナノワイヤーデバイスを検討します。

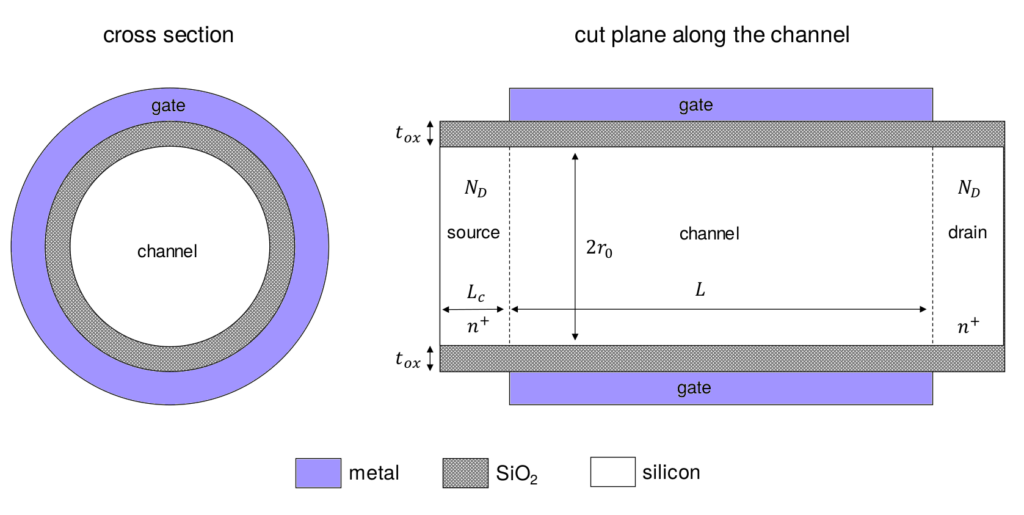
Fig. 2.1.1 検討中のナノワイヤーの構造（画像はマギル大学の Qing Shi 氏の提供）

ナノワイヤーは2つの同心円状の円柱でモデル化されており、\(z\) 軸に沿った共通の回転対称軸を持っています。内部の円柱はシリコンで満たされており、内部と外部の円柱に挟まれた領域によって形成されるシェルは二酸化ケイ素で満たされています。シリコンの円柱の2つの終端（ソースとドレイン）はpドープされており、中心のシリコン領域（チャネル）はドープされていません。金属ゲートはチャネルを囲んでおり、ソースおよびドレイン領域の外面はオーミック接触で平衡に保たれています。

2.1.2. 例2：ゲート量子ドット

このセクションの2つ目の例として、以下のゲート量子ドットデバイスを検討します。

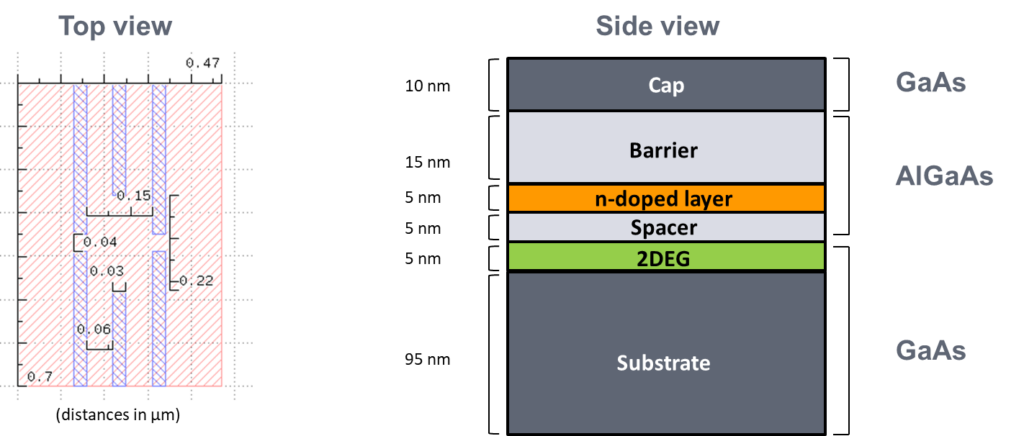
上面図（\(x\)–\(y\)平面）はこのデバイスの 2D ゲート構造のレイアウトを示しています。青い四角は\(x\)–\(y\)平面内部の閉じ込めポテンシャルを定義するための金属ゲートを表しています。さらに、赤い四角はシミュレーション領域を表しています。

側面図はチップウェハーの成長 (\(z\)) 軸に沿ったヘテロ構造の積層を表しています。AlGaAs の伝導帯端エネルギーが GaAs よりも高いので、AlGaAs 層は基板と上部ゲートの伝導を妨げるポテンシャル障壁として作用します。加えて、AlGaAs 層へのドープはバンド曲がりの原因になり、三角形の閉じ込めポテンシャル井戸が GaAs 基板と AlGaAs の界面で形成されます。これは、上図で “2DEG” とラベルされた領域で発生します。

上部ゲートによって生成される \(x\)–\(y\) 平面の閉じ込めとヘテロ構造によって提供される \(z\) 方向に沿った閉じ込めのによって、2DEG領域と \(x\)–\(y\) 平面の中心（上部ゲートの間）に束縛状態が存在することが予想されます。これらの束縛状態は量子ドットを実装する際に用いられることがあります。

2.2. 構造の指定とメッシング

このサブセクションでは、デバイスの構造を Gmsh ワークフロー（例1）および devicegen ワークフロー（例2）を用いてどのように指定するかを説明します。

2.2.1. 領域と境界

それぞれのワークフローで構造の指定を説明する前に、デバイス構造の一般的な特徴を議論する必要があります。

すべてのデバイスは下に示したように領域と境界に分けることができます。

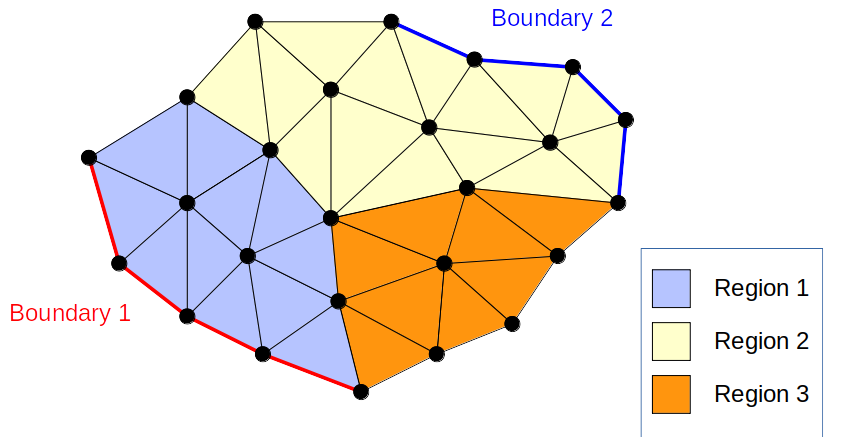
上図では、円は有限要素節点、直線は要素辺を表します。

領域は数字や文字列でラベル付けされたシミュレーション領域のサブセットです。領域はマテリアルもしくは物理量（例：ドープ密度）と関連しています。ナノワイヤーの例（例1）では、これらの領域はソース、ドレイン、チャネルで、酸化物が周りにあります。次元に応じて、領域は体積（3D シミュレーション）、面積（2D シミュレーション）、長さ（1D シミュレーション）になります。

他にも、境界は表面（3D シミュレーション）、曲線（2D シミュレーション）、点（1D シミュレーション）となり、数字や文字列でラベルされます。QTCAD で微分方程式を解く際は、これらの構造エンティティを境界条件を特定するのに用います（例：ポアソン方程式）。

2.2.2. Gmsh を用いた任意の構造の定義

Gmsh を用いることで、任意の 1D, 2D, 3D デバイス構造を定義し、メッシュを作成することができます。加えて、Gmsh を用いることで、物理的なボリューム、表面、曲線、点に至るまで領域と境界にラベル付けできます。ナノワイヤーの例（例1）では、以下のようなラベル付けをしました。

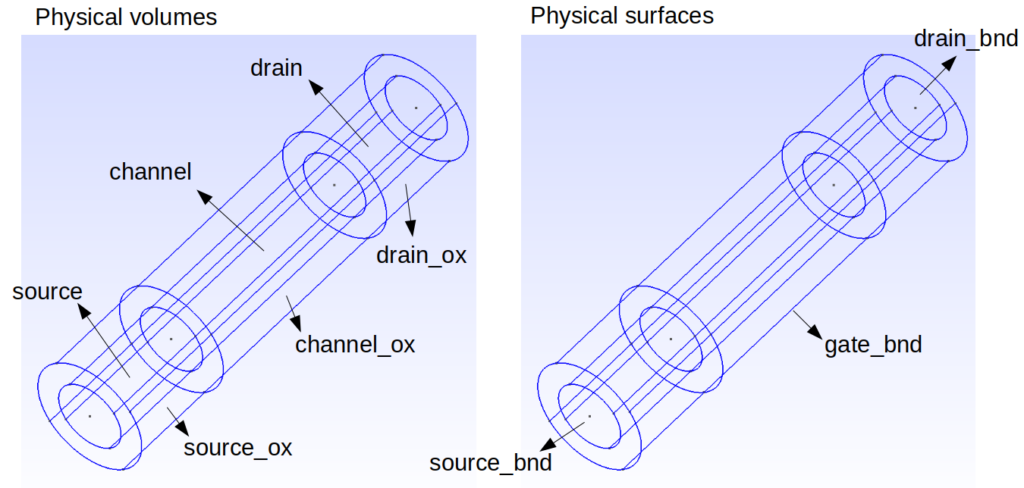
Fig. 2.2.2 ナノワイヤーに対する *`Gmsh`* の物理的なボリュームと表面のラベル

Gmsh での任意の構造の定義やメッシングのやり方を学習するには、公式の Gmsh チュートリアルをお勧めします。YouTube にもこちらのように基礎的な内容を網羅した良いチュートリアルがあります。

Gmsh のコアはスクリプト言語ですが、基礎的なグラフィカルユーザーインターフェイス (GUI) が付属しており、直感的に可視化や構造の定義ができます。それぞれの GUI アクションには同等のスクリプトが存在し、.geo ファイルに保存されます。

.geo ファイル（qtcad/examples/tutorials/meshes/nanowire.geo）によって、例1のナノワイヤーの構造を生成できます。このファイルは説明も兼ねており、底のドレインと酸化物表面を作成し、酸化物に囲まれた半導体ナノワイヤーを形成するために、\(z\) 方向に沿ってそれらを押し出します。Gmsh のドキュメントを読んでいれば、この簡単なスクリプトを理解できると思います。Gmsh GUI で構造を描画することで、簡単なスクリプトを直感的に作成できます。

QTCAD とインテグレーションするために最も重要なコードはデバイスの物理的なボリュームと表面の定義です。これは nanowire.geo ファイルの 66-68 行、

Physical Surface("drain_bnd") = {1};
Physical Volume("drain") = {volume_drain};
Physical Volume("drain_ox") = {volume_drain_ox};

86-89 行、

Physical Volume("channel") = {volume_channel};
Physical Surface("gate_bnd") = {sides_channel_ox[0],
    sides_channel_ox[1], sides_channel_ox[2], sides_channel_ox[3]};
Physical Volume("channel_ox") = {volume_channel_ox};

107-109 行で実行されます。

Physical Surface("source_bnd") = {top_source};
Physical Volume("source") = {volume_source};
Physical Volume("source_ox") = {volume_source_ox};

重要なのは、これらの行ではデバイスボリューム、表面のラベル（例："channel"）を指定しており、QTCAD の関数で様々な物理量に割り当てるのに使用します。

他で重要なのはメッシュを生成、保存する箇所です。これは、nanowire.geo ファイルの111-114 行で実行されます。

Mesh 1;
Mesh 2;
Mesh 3;
Save "nanowire.msh";

QTCAD は現在 .msh2 および .msh4 （.mshと同等）形式をサポートしています。

nanowire.geo ファイルで生成されたメッシュを可視化し、QTCAD ディレクトリのルートに .msh 形式で保存するには以下を実行します。

gmsh examples/tutorials/meshes/nanowire.geo

これで、.geo ファイルと同じディレクトリにメッシュファイル (nanowire.msh)が保存されます。

2.2.3. devicegen を用いた平面構造の指定

Gmsh は便利で自由度が高いですが、GUI やスクリプトを使って明示的にデバイス構造を定義するには時間がかかる場合があります。

特に、ゲート量子ドットは個々の電子や正孔を閉じ込めるために、複雑な 2D のゲートパターンを表示する必要があります。例えば、Fig. 2.1.2 では、6つの個別の上部ゲートがあり、量子ドットの数が増えるにつれてゲート数は急速に増加します。ヘテロ構造の積層に加えて、これらのゲートを手動で定義するのは煩雑なことがあります。

平面のデバイス構造を定義する際は、devicegen の方が便利な場合があります。devicegen パッケージは依存関係として Gmsh を使用しており、特定の構造をより簡単に生成できます。実際に、devicegen はゲートパターンを定義したテキストの GDS ファイルからレイアウトを読み込むことができます。よて、成長軸（ヘテロ構造の積層）に対称な構造は devicegen の簡単な Python API で定義できます。生成した構造は最終的に .msh 形式で出力できます。

devicegen のさらなる使い方を学ぶには、devicegen チュートリアルがお勧めです。Fig. 2.1.2. の構造の作成方法が詳細に説明されています。

加えて、devicegen は現在オープンソース（GPLライセンス）としてリリースされています。実際に、devicegen で直接コード化されていない特別な設計ルールを考えている熱心なユーザーには、GitHub の公開リポジトリでパッケージの修正を提案していただいています。

Gmsh と同じように、devicegen は領域と境界にラベルを付けることができ、.msh ファイルでメッシュを保存できます。この情報は次にシミュレーションを行う系の物理モデルの定義に使用されます。

2.3. 物理問題の指定と解法

ひとたびメッシュを生成して .msh 形式で保存すれば、Python API で QTCAD に読み込むことができます。さらに、デバイスオブジェクト（マテリアル、ドープ密度、境界条件等）を指定し、関連するソルバーをインスタンス化、実行します。

QTCAD ではいくつかのソルバーが利用でき、その使い方を学習するにはスピン量子ビットや超伝導回路のチュートリアルがお勧めです。ですが、すべての QTCAD のシミュレーションは共通の構造を使用しており、QTCAD の非常に基礎的なコードと共に例1と例2で説明しています。これらのシミュレーションでは、非線形ポアソン方程式を解いており、古典的なキャリアリザーバーの存在下でゲートポテンシャルに対する静電ポテンシャルを得ることができます。

これは、古典計算ではありますが、QTCAD で重要な役割を持ち、得られた静電ポテンシャルはデバイスの電子もしくは正孔の閉じ込めポテンシャルを計算するために使用されます。このポテンシャルはナノ構造の電子もしくは正孔の有効シュレーディンガー方程式を定義するために使用され、束縛状態を計算し、多体ハミルトニアンを書き下し、量子ドット系の化学ポテンシャルを得るために対角化を行います。

これらの例では、簡単な計算を実行する最小限のコードを示しています。詳細を知りたい場合は、スピン量子ビットや超伝導回路のチュートリアルにより発展的な機能が記載されています。加えて、以下で使用している API コマンドは API Reference でより詳細（すべての引数の詳細な説明を含む）に説明しています。

2.3.1. 例1：ナノワイヤー

この例では、examples/tutorials/meshes/nanowire.geo で生成されたメッシュに対する上述した簡単なシミュレーションを実行します。ここでは、スクリプトの構造に着目し、この例のより詳細についてはナノワイヤー量子ドットのポアソンおよびシュレーディンガー方程式シミュレーションをご確認ください。

始めに、QTCAD API の関連したモジュールを読み込みます。

from qtcad.device import constants as ct
from qtcad.device.mesh3d import Mesh
from qtcad.device import materials as mt
from qtcad.device import Device
from qtcad.device.poisson import Solver

pathlib もインポートし、インポートしたいメッシュファイルへのパスを定義します。実行している Python スクリプトの隣に meshs ディレクトリがあることを仮定しています。

import pathlib

script_dir = pathlib.Path(__file__).parent.resolve()
path_mesh = script_dir / "meshes/" / "nanowire.msh"

次に、メッシュを読み込み、このメッシュを引数にして Device オブジェクトをインスタンス化します。

scaling = 1e-9
mesh = Mesh(scaling, str(path_mesh))
d = Device(mesh)

Mesh コンストラクタの最初の引数は長さの単位を指定します。QTCAD は SI 単位系を使用するため、scaling=1e-9 はメッシュファイルの長さの単位をナノメートルにすることを意味します。

デバイスオブジェクトをインスタンス化した後は、始めに領域、次に境界を定義します（境界条件をご参照ください）。境界の前に領域を定義することが重要で、これは、境界の静電ポテンシャルを決定する数学的な方程式が、定義した領域で指定したパラメータ（例：ドープ密度）に依存するためです。

d.new_region('channel_ox',mt.SiO2)
d.new_region('source_ox',mt.SiO2)
d.new_region('drain_ox',mt.SiO2)
d.new_region('channel', mt.Si)
d.new_region('source', mt.Si, pdoping=5e20*1e6, ndoping=0)
d.new_region('drain', mt.Si, pdoping=5e20*1e6, ndoping=0)

d.new_ohmic_bnd('source_bnd')
d.new_ohmic_bnd('drain_bnd')

Vgs = 0.5
Ew = mt.Si.chi + mt.Si.Eg/2
d.new_gate_bnd('gate_bnd',Vgs,Ew)

上のコードでは、ソースとドレインがドープ密度 \(5\times 10^{20} \textrm{ cm}^{-3}\) （\(\textrm{m}^{-3}\) に変換するために \(10^6\) を掛けています）で p ドープされており、チャネルは真性シリコンで、ソース、チャネル、ドレインはシリコン酸化物で覆われています。

デバイスの領域と境界を構成した後は、非線形ポアソンソルバーをインスタンス化し、実行することができます。

s = Solver(d)
s.solve()

得られた静電ポテンシャルはデバイスの属性 phi に保存されます。

2.3.2. 例2：ゲート量子ドット

2つ目の例では、devicegen チュートリアルで生成した .msh ファイルを用いたゲート量子ドットシミュレーションを検討します。

例1と同じように、始めに関連するモジュールをインポートします。

from qtcad.device import constants as ct
from qtcad.device import materials as mt
from qtcad.device.mesh3d import Mesh
from qtcad.device import Device
from qtcad.device.poisson import Solver, SolverParams

import pathlib

このとき、実行しているPython スクリプトの隣に meshes ディレクトリがあることを仮定して、devicegen チュートリアルで生成した gated_dot.msh ファイルをインポートします。このメッシュに対するデバイスオブジェクトをインスタンス化します。

script_dir = pathlib.Path(__file__).parent.resolve()
path_mesh = str(script_dir/'meshes'/'gated_dot.msh')

scaling = 1e-6
mesh = Mesh(scaling,path_mesh)
d = Device(mesh)
d.set_temperature(0.1)

ここで、デバイス温度を \(0.1\textrm{ K}\) に設定します（温度は均一とします）。

次に、チュートリアルでラベルしたそれぞれの領域にマテリアルを設定します。

d.new_region("cap", mt.GaAs)
d.new_region("barrier", mt.AlGaAs)
d.new_region("dopant_layer", mt.AlGaAs, ndoping=3e18*1e6)
d.new_region("spacer_layer", mt.AlGaAs)
d.new_region("spacer_dot", mt.AlGaAs)
d.new_region("two_deg", mt.GaAs)
d.new_region("two_deg_dot", mt.GaAs)
d.new_region("substrate", mt.GaAs)
d.new_region("substrate_dot", mt.GaAs)

マテリアルを設定したときは、ヘテロ界面を横切ってバンドを配置することが重要です。デフォルトでは、QTCAD はバンドアライメントにアンダーソンの法則を使用します。しかし、アンダーソンの法則は定性的にのみ正しいことが知られています。GaAs/AlGaAs ヘテロ界面では、弊社の原子論的シミュレーションコード RESCU を用いてより正確なバンドアライメントパラメータを計算しています（こちらをご確認ください）。このバンドアライメントモデルは次のように有効化します。

d.align_bands(mt.GaAs)

前と同じように、系の境界条件を設定します。ここで、シミュレーションドメインの最下部の表面（Fig. 2.1.2 の基板の底）にオーミック境界条件を使用します。また、すべての上部ゲートにショットキー境界を使用し、印加ポテンシャルとショットキー障壁を引数に取ります。

d.new_ohmic_bnd("back_gate")

barrier = 0.834*ct.e
d.new_schottky_bnd("top_gate_1", -0.5, barrier)
d.new_schottky_bnd("top_gate_2", -0.5, barrier)
d.new_schottky_bnd("top_gate_3", -0.5, barrier)
d.new_schottky_bnd("bottom_gate_1", -0.5, barrier)
d.new_schottky_bnd("bottom_gate_2", -0.5, barrier)
d.new_schottky_bnd("bottom_gate_3", -0.5, barrier)

次に、ポアソンソルバーをインスタンス化し、実行します。

solver_params = SolverParams({"tol": 1e-3, "maxiter": 100})
solver = Solver(d, solver_params=solver_params)
solver.solve()

ここで、ポアソンソルバーのパラメータを設定するのに使用する SolverParams オブジェクトを定義します。また、自己無撞着ソルバーの公差（引数 tol）を \(10^{-3}\textrm{ V}\) に、反復の最大回数（引数 maxiter）を \(100\) に設定します。これは、自己無撞着の繰り返しは2つの成功した反復の静電ポテンシャルの最大差が \(1\textrm{ mV}\) よりも小さいときに終了することを意味し、反復の最大回数に達した場合は、警告メッセージと共に強制的に停止します。Solver クラスを定義しているそれぞれのモジュールが関連する SolverParams クラスを持っていることに注意してください。ここでは、明らかなように poisson モジュールの SolverParams クラスを使用しています。

2.4. 後処理

シミュレーションが完了すると、結果の可視化や定性的もしくは定量的な解析を実行することができます。

QTCAD では、主に2つの可視化方法があります。

QTCAD の analysis モジュール
ParaView

analysis モジュールでは、プロット、ラインカット、スライス、その他可視化ツールを QTCAD のスクリプトから直接実行できます。analysis モジュールは 2D プロットでは Matplotlib、3D プロットでは PyVista を利用しています。

ParaViewでは、シミュレーションの結果を .vtu ファイルとして保存でき、オープンソースでマルチプラットフォームの 3D データ解析および可視化アプリケーショの ParaView で読み込むことができます。

ParaView は非常に強力で analysis モジュールと比べてかなり多機能なので、重要なデータ解析にはこちらをお勧めします。しかしながら、簡単なプロットや整合性の確認においては、QTCAD API のみでプロットできる analysis モジュールが便利なこともあります。こちらはほとんどのチュートリアルで実施されています。

ここでは、例1（ナノワイヤー）で両手法をどのように使用するかを簡単に示します。例2でも同じコマンドが使用できます。

2.4.1. `analysis` モジュールを用いた後処理

始めに、analysis モジュールをインポートします。

from qtcad.device import analysis

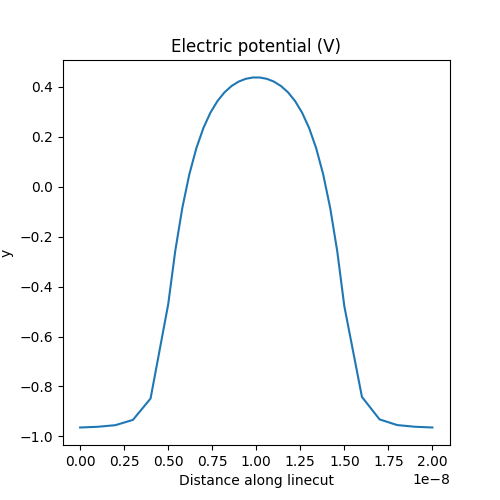
このとき、\(z\) 軸（円柱の対称軸）に沿ってラインカットの静電ポテンシャルをプロットします。

analysis.plot_linecut(mesh,d.phi,(0,0,0),(0,0,20e-9),
   title='Electric potential (V)')

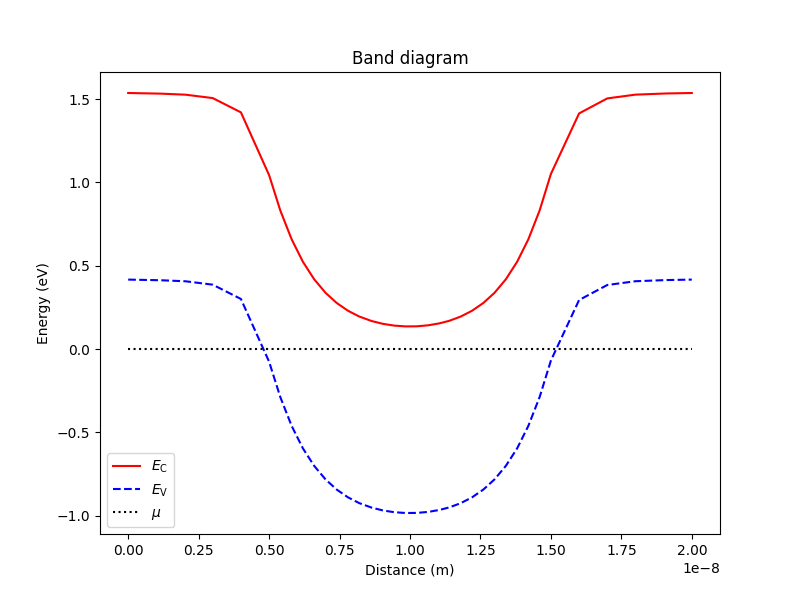
同じラインカットの沿ったバンドダイアグラムもプロットできます。

最後に、デバイスの垂直なスライスに沿った 3D 密度プロットを可視化することもできます。

analysis.plot_slices(mesh,d.p/1e6,title='p (cm^-3)')

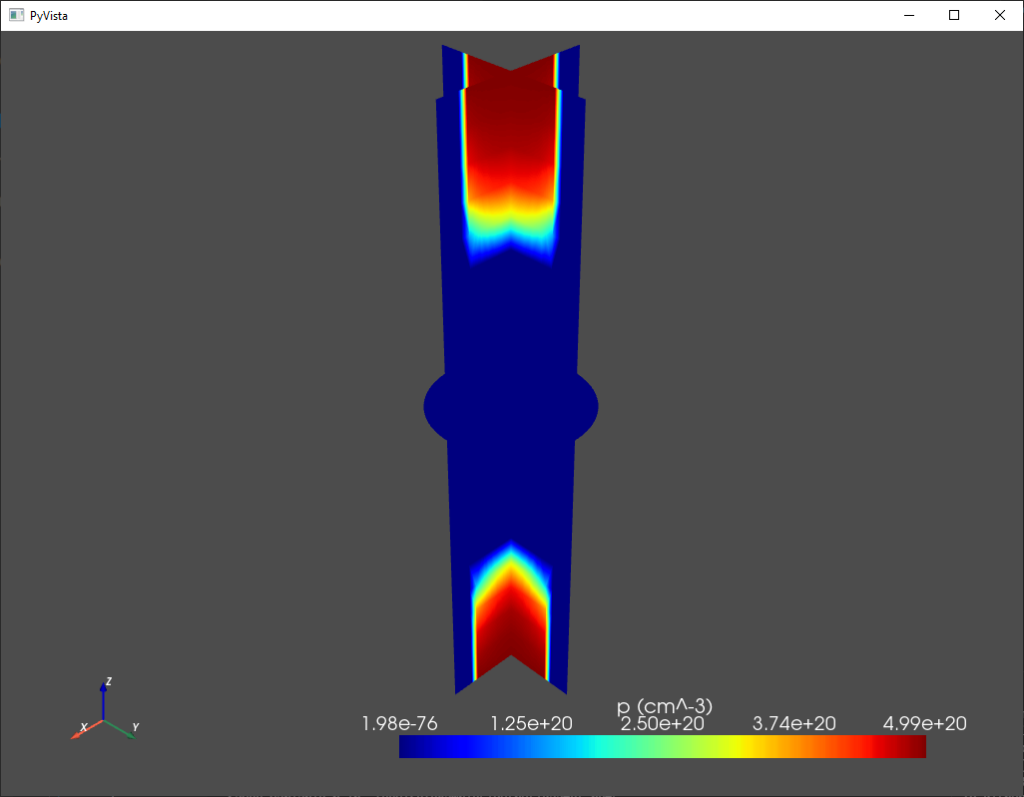
デフォルトでは、垂直なスライスはそれぞれのカーテシアン方向に沿ったシミュレーションドメインの中間にあります。このスライスの位置は plot_slices 関数の 'x', 'y', 'z' キーワード引数で変更できます。より発展的なデータの可視化には、ParaView をお勧めします。

2.4.2. ParaView を用いた後処理

ParaView の後処理を行うには、始めに .vtu 形式で可視化する物理量を保存する必要があります。

始めに io モジュールをインポートして、ファイルの保存と読み込みを有効にします。

from qtcad.device import io

次に、可視化したいすべての変数を含むディクショナリーを作成します。

vars_dict = {"n": d.n/1e6, "p": d.p/1e6, "phi": d.phi,
   "EC": d.cond_band_edge()/ct.e, "EV": d.vlnce_band_edge()/ct.e}

ディクショナリーのキーは変数名に対応し、出力ファイルは ParaView に読み込まれます。加えて、SI 単位系の \(\textrm{cm}^{-3}\) に変換するために \(10^{6}\) で密度を割っています。また、ParaView でプロットする際に、ジュールの代わりに eV を使用するために電気素量で伝導帯端と価電子帯端を割っています。

path_vtu = script_dir / "nanowire.vtu"
io.save(path_vtu, vars_dict, mesh)

vars_dict ディクショナリーの中身はメッシュと共に保存されます。

io モジュールのパスとして認識させるために、.vtu 拡張子を使用します。.vtu ファイルを保存すると、ParaView の高度なプロット機能を使用することができます。ParaView のより詳細な情報は ParaView を用いた QTCAD 物理量の可視化や直接 ParaView のウェブサイトをご確認ください。

2.5. コード構造とワークフロー

結論として、QTCAD シミュレーションのワークフローは以下のようにまとめられます。

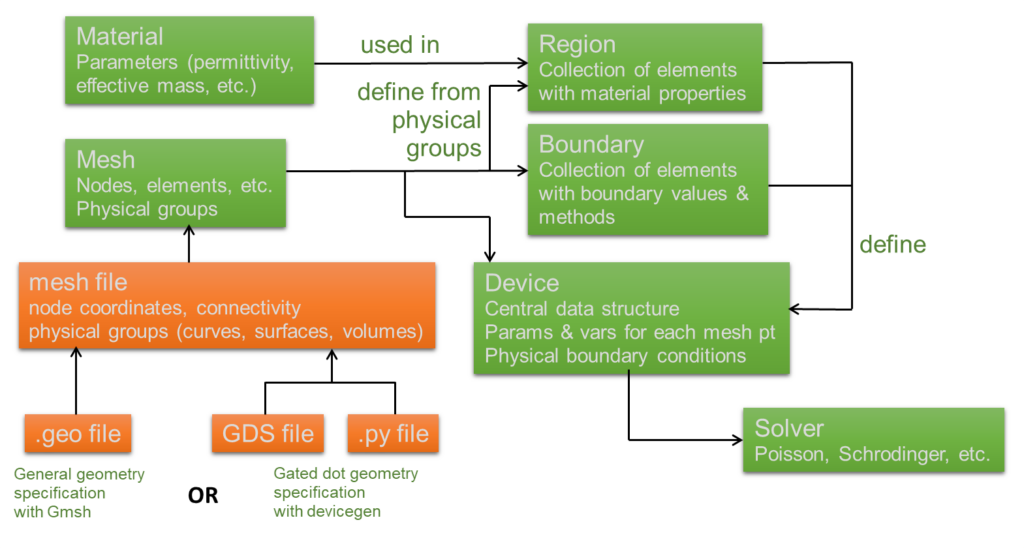
オレンジの四角はNanoacademic 製品ではない外部の機能で、緑の四角は内部のモジュールやクラスを示しています。また、これらの緑の四角は有限要素シミュレーション用の Python API をサポートしています。