PeakFit チュートリアル
PeakFit チュートリアル 隠れたピークのフィッティング
- PeakFit の起動
- 隠れたピークを持つデータ
- SAMPLE.XLS ファイルのインポート
- 残差 (Residuals) による自動フィッティング
- 振幅の閾値設定
- 隠れた残差ピークの追加
- フィッティングのアップデート
- 2次導関数を用いた自動フィッティング
- フィッティングの設定
- 制約条件 (Constraint)
- 数値フィッティング
- 正規分布の誤差
- 畳み込みによる自動フィッティング
- グラフ上での調整
1．PeakFit の起動
PeakFit のアイコンまたはスタートメニューのショートカットをクリックして起動させます。
2．隠れたピークを持つデータ
このチュートリアルでは、ノイズの乗ったサンプルデータを使用して説明します。データには全部で 15 のピークがあり、そのうち 4つはピークがあるようには見えない隠れたピークです。このデータは、x が 1.0 から 8.5 の間に 0.5 間隔でピークが配置されています。ただし、例外として x=4.5 の位置にはピークはありません。ノイズの乗ったデータをシミュレートするために、5％ のランダムなガウスノイズを適用します。
3．SAMPLE.XLS ファイルのインポート
PeakFit のすべてのサンプルデータは、1枚の Excel ワークシート SAMPLE.XLS に用意されています。データセット毎にシートやページが分けてあります。まず最初のシートをインポートします。
1.File メニューの Import オプションまたは最初のツールバーアイコン 
をクリックします。ファイルの種類を Excel にして sample.xls をインポートします。
2.変数 x に A!A を、変数 Y に A!B 列を指定します。PeakFit は Excel 風のシートまたページの指定方法を採用しています。
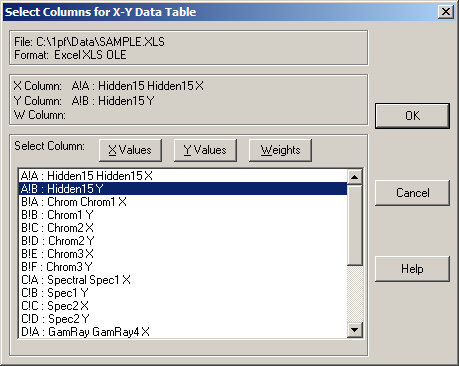
3.OK ボタンをクリックして確定します。次にタイトルを設定するダイアログが表示されます。ここでは OK ボタンをクリックして、スプレッドシートのタイトルをそのまま採用します。
4．残差 (Residuals) による自動フィッティング
1.AutoFit メニューの AutoFit Peaks I Residuals オプションを選択するか、山印にローマ数字の 1 が描かれたツールバーボタン 
をクリックします。
サンプルデータにはかなりのノイズが乗っているため、デフォルト設定の平滑化レベルと振幅の閾値は十分ではありません。最初に 100 個のガウス関数のピークが表われます。
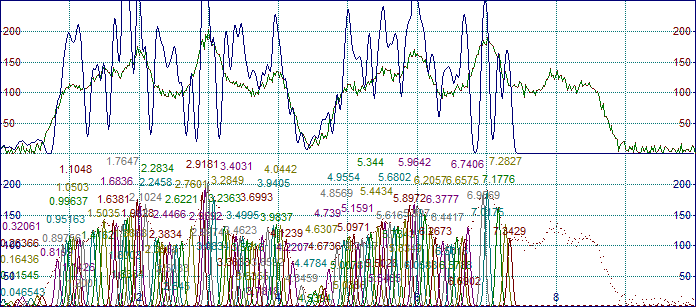
2.平滑化 (Smoothing) レベル（Sm%）の隣にある AI エキスパートボタン 
をクリックします。
PeakFit には、最適な平滑化レベルを求めるアルゴリズムが搭載されています。このデータセットの場合、Savitzky-Golay 平滑化ウィンドウは約 5％ に設定されているでしょう。
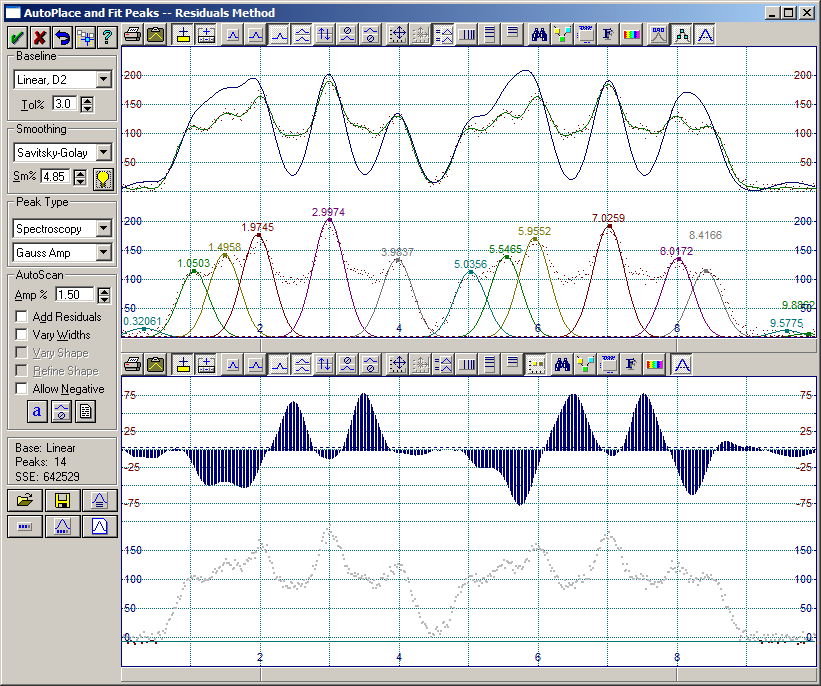
グラフの上側エリアにある上プロットには、3つの要素が表示されています。すなわち、元データからベースライン推定値を引いた値、平滑化されたデータ、そしてすべてのピークを合成して作られたカーブです。下プロットは、個々のピークを表しています。
グラフの下側エリアにある上プロットは、残差すなわち平滑化されたデータと合成カーブの y 値差分です。下プロットは、自動ベースラインフィッティングの切換えポイントと元データです。
5．振幅の閾値設定
データの両端にあるノイズから、2つのピークが表われていることに注意して下さい。
1.これを消去するために Amp%（振幅の閾値）を 8% に設定します。
直接数値を入力しても、スピンボタンあるいは右クリックして表示されたポップアップメニューを使って 8％ と入力することもできます。振幅の閾値は、プロット中では点線で表示されています。
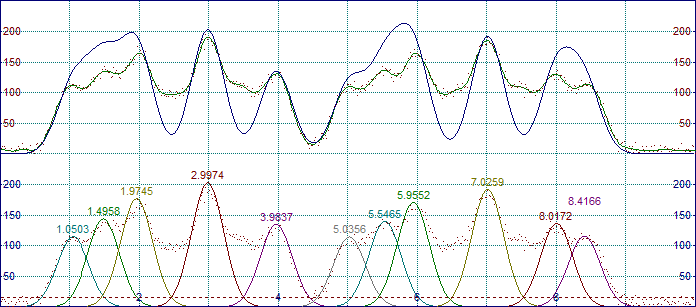
6．隠れた残差ピークの追加
この時点で、11 個のピークが発見できました。残差グラフは、閾値 8％ の上に非常にはっきりと 4つのピークが隠れていることを示しています。
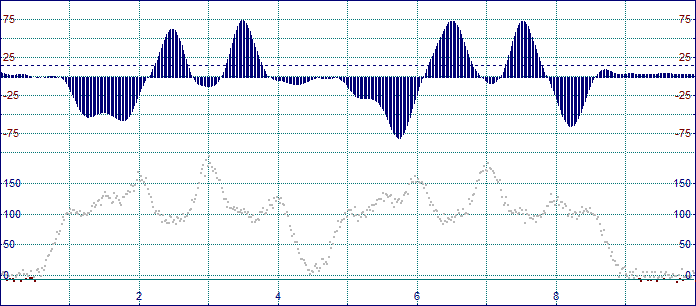
1.この 4つのピークを全体の中に自動で加えるために、Add Residuals ボックスをクリックします。
すると、15個のピークが表示されます。
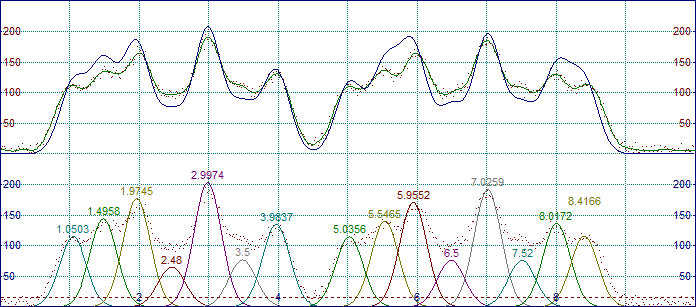
このデータセットでは、デフォルトのリニアベースライン、ガウス関数のピーク、固定幅の設定を使用しました。Vary Widths をオフに設定すると、ピークの幅は 1 となります。
7．フィッティングのアップデート
フィッティングをアップデートします。すなわち、全体の評価関数がよくなるようにフィッティングを繰り返します。
1.コントロールパネル下部にある Full Peak Fit with Graphical Update ボタン 
をクリックします。
繰り返しが表示されます。この図では r2 値が 0.99087 になるまで 9 回フィッティングが繰り返されています。
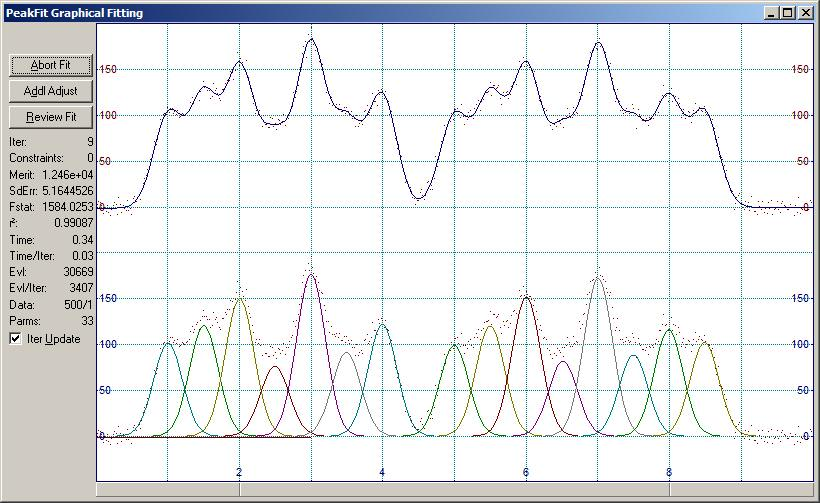
2.Review Fit をクリックしてレポートを表示します。
PeakFit のレポートは、デスクトップ形式になっています。メインのピークフィッティングのグラフのほか残差グラフ、計算値レポート、データレポートなど、必要なものがすべて表示されます。ここでは、それらのオプションのいくつかを見てみましょう。
フィッティングされたデータポイントは、標準偏差によって色分けされています。背景が黒のデフォルトカラー設定では、赤のポイントは 3σ の外、黄色が 2σ の外になります。
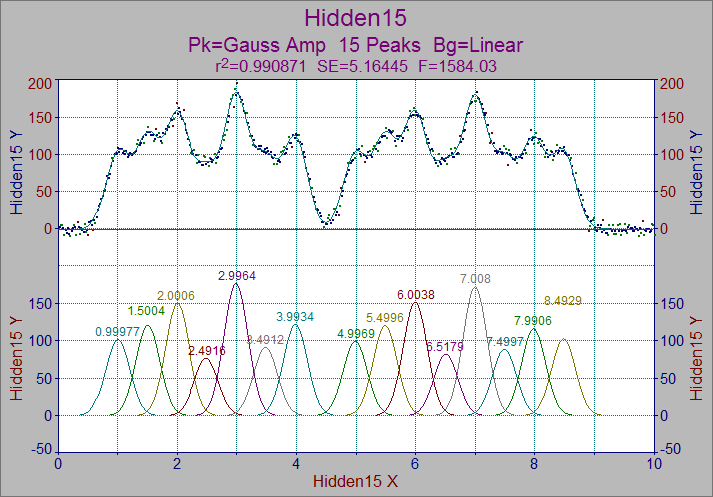
3.ツールバーの右側にある Select Function Labels ボタン 
をクリックします。
4.ラベルとして Area Parameter を選択します。
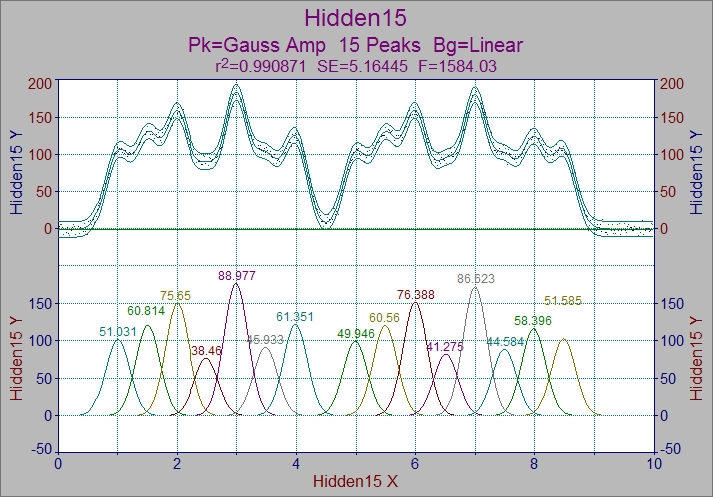
ガウス関数でフィッティングを行いましたが、フィッティングパラメータから解析領域を計算することができます。すなわち各ピークの面積が表示されます。
5.ツールバーの右側にある Show Confidence/Prediction Intervals ボタン 
をクリックします。フィッティング曲線の 95％信頼区間が表示されます。
Set Confidence/Prediction Intervals, % Confidence ボタン 
を使って、信頼区間と予測区間の表示／非表示設定と90／95／99％信頼区間の選択ができます。
6.表示区間をチェックした後、Show Confidence/Prediction Intervals ボタン をクリックすると設定が切り替わります。
ピークフィッティングでは、数値データは非常に重要です。PeakFit は、そのレポートを表示してくれます。
7.Numeric ボタンをクリックします。
Fitted Parameters
r2 Coef Det DF Adj r2 Fit Std Err F-value
0.99087103 0.99022455 5.16445263 1584.02528
Peak Type a0 a1 a2
1 Gauss Amp 101.350053 0.99977381 0.20087369
2 Gauss Amp 120.777814 1.50036843 0.20087369
3 Gauss Amp 150.244205 2.00059637 0.20087369
4 Gauss Amp 76.3834430 2.49163548 0.20087369
5 Gauss Amp 176.712313 2.99643241 0.20087369
6 Gauss Amp 91.2243268 3.49117978 0.20087369
7 Gauss Amp 121.844896 3.99335264 0.20087369
8 Gauss Amp 99.1953657 4.99687327 0.20087369
9 Gauss Amp 120.274614 5.49962035 0.20087369
10 Gauss Amp 151.709148 6.00378274 0.20087369
11 Gauss Amp 81.9743916 6.51785997 0.20087369
12 Gauss Amp 172.036096 7.00799405 0.20087369
13 Gauss Amp 88.5446586 7.49967219 0.20087369
14 Gauss Amp 115.977346 7.99063147 0.20087369
15 Gauss Amp 102.449403 8.49286836 0.20087369
B Linear Bg -1.1308483 0.08609085
Fitted Parameters セクションには、すべてのピークに関する統計データが表示されます。
Measured Values
Peak Type Amplitude Center FWHM Asym50 FW Base Asym10
1 Gauss Amp 101.350053 0.99977381 0.47302139 1.00000000 0.94685080 1.00000000
2 Gauss Amp 120.777814 1.50036843 0.47302139 1.00000000 0.94685080 1.00000000
3 Gauss Amp 150.244205 2.00059638 0.47302139 0.99999994 0.94685080 0.99999996
4 Gauss Amp 76.3834430 2.49163547 0.47302139 1.00000004 0.94685080 1.00000002
5 Gauss Amp 176.712313 2.99643241 0.47302139 1.00000001 0.94685080 1.00000001
6 Gauss Amp 91.2243268 3.49117978 0.47302139 1.00000000 0.94685080 1.00000000
7 Gauss Amp 121.844896 3.99335264 0.47302139 1.00000003 0.94685080 1.00000002
8 Gauss Amp 99.1953657 4.99687329 0.47302139 0.99999988 0.94685080 0.99999993
9 Gauss Amp 120.274614 5.49962035 0.47302139 1.00000000 0.94685080 1.00000001
10 Gauss Amp 151.709148 6.00378274 0.47302139 0.99999999 0.94685080 1.00000000
11 Gauss Amp 81.9743916 6.51785997 0.47302139 1.00000000 0.94685080 1.00000000
12 Gauss Amp 172.036096 7.00799404 0.47302139 1.00000004 0.94685080 1.00000002
13 Gauss Amp 88.5446586 7.49967219 0.47302139 1.00000000 0.94685080 1.00000000
14 Gauss Amp 115.977346 7.99063147 0.47302139 1.00000007 0.94685080 1.00000003
15 Gauss Amp 102.449403 8.49286836 0.47302139 1.00000000 0.94685080 1.00000000
Peak Type Anlytc Area % Area Int Area % Area Centroid Moment2
1 Gauss Amp 51.0313391 5.72373428 51.0313117 5.72373138 0.99977436 0.04034970
2 Gauss Amp 60.8135210 6.82091517 60.8135210 6.82091538 1.50036843 0.04035024
3 Gauss Amp 75.6503105 8.48502672 75.6503105 8.48502698 2.00059637 0.04035024
4 Gauss Amp 38.4602600 4.31374745 38.4602600 4.31374758 2.49163548 0.04035024
5 Gauss Amp 88.9774175 9.97981053 88.9774175 9.97981083 2.99643241 0.04035024
6 Gauss Amp 45.9328775 5.15188491 45.9328775 5.15188507 3.49117978 0.04035024
7 Gauss Amp 61.3508139 6.88117857 61.3508139 6.88117878 3.99335264 0.04035024
8 Gauss Amp 49.9464205 5.60204855 49.9464205 5.60204872 4.99687327 0.04035024
9 Gauss Amp 60.5601521 6.79249702 60.5601521 6.79249723 5.49962035 0.04035024
10 Gauss Amp 76.3879326 8.56775927 76.3879326 8.56775953 6.00378274 0.04035024
11 Gauss Amp 41.2753902 4.62949572 41.2753902 4.62949587 6.51785997 0.04035024
12 Gauss Amp 86.6228693 9.71572166 86.6228693 9.71572196 7.00799405 0.04035024
13 Gauss Amp 44.5836226 5.00055091 44.5836226 5.00055107 7.49967219 0.04035024
14 Gauss Amp 58.3964107 6.54980927 58.3964107 6.54980947 7.99063147 0.04035024
15 Gauss Amp 51.5848791 5.78581997 51.5848791 5.78582015 8.49286836 0.04035024
Total 891.574217 100.000000 891.574189 100.000000
Measured Values セクションには、各ピークのプロパティが表示されます。順番に振幅、中央値、半半値幅、半値非対称性、ピーク底部の全幅推定値、10％での非対称性です。そのつぎの表は、推定面積、X最小／最大値間の面積、1次および 2次モーメントです。
Parameter Statistics
Peak 1 Gauss Amp
Parm Value Std Error t-value 95% Confidence Limits P>|t|
Amp 101.350053 1.77558396 57.0798425 97.8609294 104.839176 0.00000
Ctr 0.99977381 0.00506103 197.543354 0.98982859 1.00971904 0.00000
Wid 0.20087369 0.00119183 168.542173 0.19853167 0.20321570 0.00000
Peak 2 Gauss Amp
Parm Value Std Error t-value 95% Confidence Limits P>|t|
Amp 120.777814 1.87410471 64.4456060 117.095091 124.460536 0.00000
Ctr 1.50036843 0.00570802 262.852866 1.48915186 1.51158501 0.00000
Wid 0.20087369 0.00119183 168.542173 0.19853167 0.20321570 0.00000
Peak 3 Gauss Amp
Parm Value Std Error t-value 95% Confidence Limits P>|t|
Amp 150.244205 1.87528190 80.1181970 146.559169 153.929240 0.00000
Ctr 2.00059637 0.00495961 403.377433 1.99085045 2.01034230 0.00000
Wid 0.20087369 0.00119183 168.542173 0.19853167 0.20321570 0.00000
Peak 4 Gauss Amp
Parm Value Std Error t-value 95% Confidence Limits P>|t|
Amp 76.3834430 1.91610147 39.8639864 72.6181948 80.1486911 0.00000
Ctr 2.49163548 0.00976476 255.166068 2.47244717 2.51082379 0.00000
Wid 0.20087369 0.00119183 168.542173 0.19853167 0.20321570 0.00000
Peak 5 Gauss Amp
Parm Value Std Error t-value 95% Confidence Limits P>|t|
Amp 176.712313 1.80993172 97.6347953 173.155694 180.268931 0.00000
Ctr 2.99643241 0.00413044 725.451006 2.98831586 3.00454896 0.00000
Wid 0.20087369 0.00119183 168.542173 0.19853167 0.20321570 0.00000
Peak 6 Gauss Amp
Parm Value Std Error t-value 95% Confidence Limits P>|t|
Amp 91.2243268 1.84041666 49.5672143 87.6078036 94.8408500 0.00000
Ctr 3.49117978 0.00753689 463.212403 3.47636937 3.50599019 0.00000
Wid 0.20087369 0.00119183 168.542173 0.19853167 0.20321570 0.00000
Peak 7 Gauss Amp
Parm Value Std Error t-value 95% Confidence Limits P>|t|
Amp 121.844896 1.66637381 73.1197858 118.570377 125.119415 0.00000
Ctr 3.99335264 0.00403720 989.138615 3.98541931 4.00128598 0.00000
Wid 0.20087369 0.00119183 168.542173 0.19853167 0.20321570 0.00000
Peak 8 Gauss Amp
Parm Value Std Error t-value 95% Confidence Limits P>|t|
Amp 99.1953657 1.64780414 60.1985171 95.9573371 102.433394 0.00000
Ctr 4.99687327 0.00495603 1008.24147 4.98713440 5.00661215 0.00000
Wid 0.20087369 0.00119183 168.542173 0.19853167 0.20321570 0.00000
Peak 9 Gauss Amp
Parm Value Std Error t-value 95% Confidence Limits P>|t|
Amp 120.274614 1.75036101 68.7141757 116.835055 123.714173 0.00000
Ctr 5.49962035 0.00554121 992.494622 5.48873156 5.51050914 0.00000
Wid 0.20087369 0.00119183 168.542173 0.19853167 0.20321570 0.00000
Peak 10 Gauss Amp
Parm Value Std Error t-value 95% Confidence Limits P>|t|
Amp 151.709148 1.73873455 87.2526218 148.292436 155.125860 0.00000
Ctr 6.00378274 0.00457343 1312.75156 5.99479568 6.01276980 0.00000
Wid 0.20087369 0.00119183 168.542173 0.19853167 0.20321570 0.00000
Peak 11 Gauss Amp
Parm Value Std Error t-value 95% Confidence Limits P>|t|
Amp 81.9743916 1.85692454 44.1452465 78.3254295 85.6233537 0.00000
Ctr 6.51785997 0.00892161 730.570310 6.50032851 6.53539143 0.00000
Wid 0.20087369 0.00119183 168.542173 0.19853167 0.20321570 0.00000
Peak 12 Gauss Amp
Parm Value Std Error t-value 95% Confidence Limits P>|t|
Amp 172.036096 1.82456277 94.2889434 168.450727 175.621466 0.00000
Ctr 7.00799405 0.00450819 1554.50368 6.99913520 7.01685289 0.00000
Wid 0.20087369 0.00119183 168.542173 0.19853167 0.20321570 0.00000
Peak 13 Gauss Amp
Parm Value Std Error t-value 95% Confidence Limits P>|t|
Amp 88.5446586 1.89762209 46.6608495 84.8157235 92.2735938 0.00000
Ctr 7.49967219 0.00869268 862.757644 7.48259059 7.51675379 0.00000
Wid 0.20087369 0.00119183 168.542173 0.19853167 0.20321570 0.00000
Peak 14 Gauss Amp
Parm Value Std Error t-value 95% Confidence Limits P>|t|
Amp 115.977346 1.80989280 64.0796772 112.420804 119.533889 0.00000
Ctr 7.99063147 0.00605167 1320.40183 7.97873961 8.00252334 0.00000
Wid 0.20087369 0.00119183 168.542173 0.19853167 0.20321570 0.00000
Peak 15 Gauss Amp
Parm Value Std Error t-value 95% Confidence Limits P>|t|
Amp 102.449403 1.68544868 60.7846467 99.1374004 105.761405 0.00000
Ctr 8.49286836 0.00486634 1745.22662 8.48330572 8.50243100 0.00000
Wid 0.20087369 0.00119183 168.542173 0.19853167 0.20321570 0.00000
Baseline Linear Bg
Parm Value Std Error t-value 95% Confidence Limits P>|t|
a0 -1.1308483 0.99060944 -1.1415682 -3.0774521 0.81575550 0.25422
a1 0.08609085 0.12892738 0.66774683 -0.1672588 0.33944047 0.50463
Parameter Statistics セクションには、統計データが記されています。デフォルト設定の場合は、95％信頼区間のパラメータが表示されます。確率はオプションで、統計的にゼロではないパラメータが表示されます。このフィッティングの場合、バックグランドのパラメータは p=0.05 以上ですので、有意性検定には通常の範囲が使用されます。確率は、関係ないピークも含むモデル、統計的な意味をもたないピークを持つモデルの判断に使用されます。
Chromatographic Analysis Peak Type Nmoment NGauss FW Base Asym10 Resolution 1 Gauss Amp 24.7721472 24.7717937 0.94685080 1.00000000 2 Gauss Amp 55.7891485 55.7891541 0.94685080 1.00000000 0.52869430 3 Gauss Amp 99.1911328 99.1911434 0.94685080 0.99999996 0.52830704 4 Gauss Amp 153.859001 153.859016 0.94685080 1.00000002 0.51860240 5 Gauss Amp 222.516831 222.516853 0.94685080 1.00000001 0.53313250 6 Gauss Amp 302.063550 302.063581 0.94685080 1.00000000 0.52251883 7 Gauss Amp 395.211181 395.211220 0.94685080 1.00000002 0.53036113 8 Gauss Amp 618.800373 618.800438 0.94685080 0.99999993 1.05985087 9 Gauss Amp 749.582290 749.582365 0.94685080 1.00000001 0.53096757 10 Gauss Amp 893.313366 893.313455 0.94685080 1.00000000 0.53246234 11 Gauss Amp 1052.84381 1052.84391 0.94685080 1.00000000 0.54293372 12 Gauss Amp 1217.14227 1217.14239 0.94685080 1.00000002 0.51764657 13 Gauss Amp 1393.92195 1393.92209 0.94685080 1.00000000 0.51927732 14 Gauss Amp 1582.39936 1582.39952 0.94685080 1.00000003 0.51851810 15 Gauss Amp 1787.56845 1787.56863 0.94685080 1.00000000 0.53042876
Chromatographic Analysis セクションは、ピーク底部の全幅推定値や 10％ での非対称性、隣り合うピーク同士の距離などと同じように、モーメントおよびガウス関数に基づいていいます。
Overlap Areas Peak Type Peak 1 Peak 2 Peak 3 Peak 4 Peak 5 Peak 6 1 Gauss Amp 51.0313117 11.8343019 0.78910348 0.00905249 4.5065e-05 2.7089e-08 2 Gauss Amp 11.8343019 60.8135210 14.4198009 0.65594567 0.01441377 3.8139e-05 3 Gauss Amp 0.78910348 14.4198009 75.6503105 11.6865533 1.08119255 0.01218085 4 Gauss Amp 0.00905249 0.65594567 11.6865533 38.4602600 11.8213825 0.53967880 5 Gauss Amp 4.5065e-05 0.01441377 1.08119255 11.8213825 88.9774175 13.6509232 6 Gauss Amp 2.7089e-08 3.8139e-05 0.01218085 0.53967880 13.6509232 45.9328775 7 Gauss Amp 5.1674e-12 3.3335e-08 4.796e-05 0.00899588 0.96455508 11.1724976 8 Gauss Amp 1.2823e-21 1.7775e-16 5.3932e-12 1.9689e-08 4.2464e-05 0.00854201 9 Gauss Amp 2.2491e-27 1.4606e-21 2.0655e-16 3.3927e-12 3.406e-08 3.0342e-05 10 Gauss Amp 8.1374e-34 2.4943e-27 1.658e-21 1.2384e-16 5.868e-12 2.3651e-08 11 Gauss Amp 2.867e-41 4.2852e-34 1.3841e-27 4.8719e-22 1.1281e-16 2.1461e-12 12 Gauss Amp 9.573e-49 6.493e-41 9.4927e-34 1.4662e-27 1.5521e-21 1.3004e-16 13 Gauss Amp 3.3798e-57 1.0462e-48 6.9639e-41 4.7599e-34 2.3153e-27 8.6409e-22 14 Gauss Amp 4.4159e-66 6.2318e-57 1.8872e-48 5.6987e-41 1.2755e-33 2.1186e-27 15 Gauss Amp 6.3281e-76 4.2186e-66 6.0233e-57 8.3277e-49 8.8923e-41 6.8212e-34 Peak Type Peak 7 Peak 8 Peak 9 Peak 10 Peak 11 Peak 12 1 Gauss Amp 5.1674e-12 1.2823e-21 2.2491e-27 8.1374e-34 2.867e-41 9.573e-49 2 Gauss Amp 3.3335e-08 1.7775e-16 1.4606e-21 2.4943e-27 4.2852e-34 6.493e-41 3 Gauss Amp 4.796e-05 5.3932e-12 2.0655e-16 1.658e-21 1.3841e-27 9.4927e-34 4 Gauss Amp 0.00899588 1.9689e-08 3.3927e-12 1.2384e-16 4.8719e-22 1.4662e-27 5 Gauss Amp 0.96455508 4.2464e-05 3.406e-08 5.868e-12 1.1281e-16 1.5521e-21 6 Gauss Amp 11.1724976 0.00854201 3.0342e-05 2.3651e-08 2.1461e-12 1.3004e-16 7 Gauss Amp 61.3508139 0.69111425 0.01080932 3.839e-05 1.6616e-08 4.5174e-12 8 Gauss Amp 0.69111425 49.9464205 11.5723415 0.75134845 0.00695107 3.6515e-05 9 Gauss Amp 0.01080932 11.5723415 60.5601521 14.2130937 0.56165294 0.01256557 10 Gauss Amp 3.839e-05 0.75134845 14.2130937 76.3879326 11.0730036 1.01110315 11 Gauss Amp 1.6616e-08 0.00695107 0.56165294 11.0730036 41.2753902 12.9451578 12 Gauss Amp 4.5174e-12 3.6515e-05 0.01256557 1.01110315 12.9451578 86.6228693 13 Gauss Amp 1.3594e-16 2.204e-08 3.3302e-05 0.01144140 0.62329518 13.4391174 14 Gauss Amp 1.5135e-21 4.9708e-12 3.3484e-08 5.0703e-05 0.01208778 1.02496555 15 Gauss Amp 2.2972e-27 1.6556e-16 5.1941e-12 3.6419e-08 4.0739e-05 0.01460661 Peak Type Peak 13 Peak 14 Peak 15 1 Gauss Amp 3.3798e-57 4.4159e-66 6.3281e-76 2 Gauss Amp 1.0462e-48 6.2318e-57 4.2186e-66 3 Gauss Amp 6.9639e-41 1.8872e-48 6.0233e-57 4 Gauss Amp 4.7599e-34 5.6987e-41 8.3277e-49 5 Gauss Amp 2.3153e-27 1.2755e-33 8.8923e-41
Overlap Areas セクションは、特定のピーク同士が重なり合う面積％です。
Analysis of Variance r2 Coef Det DF Adj r2 Fit Std Err 0.99087103 0.99022455 5.16445263 Source Sum of Squares DF Mean Square F Regr 1351950.2 32 42248.443 1584.0253 Error 12455.624 467 26.671571 Total 1364405.8 499
Analysis of Variance セクションは、フィッティングの ANOVA を表します。たくさんのあるいは少なめのピークを比較するとき、F 統計量が役に立ちます。大きな F 統計量モデルは、非常に有効です。
Details of Fit Set Convergence State Iterations Minimization Extent 1E-6 Converged 9 Least Squares 1/1 Curvature Matrix Constraints Violated Sparse-Roots 25.0000-5.00000-50.0000- None - None 0
Details of Fit セクションは、フィッティングの概要について記しています。
数値レポートは、編集、印刷、ファイル保存、クリップボードへのコピーが行えます。Options メニューをクリックすると、各種レポートの表示／非表示を設定することができます。
次のフィッティングの結果を使って、その他のオプションを見てみましょう。
8.Numeric ボタンを押すか、直接ウィンドウを操作して数値レポートを閉じます。OK ボタンをクリックして Review Fit ウィンドウを閉じます。これで現在の設定も保存されます（設定内容は PK.CFG ファイルに保存されます）。Cancel ボタンをクリックした場合は、設定は保存されません。
8．2次導関数を用いた自動フィッティング
1.AutoFit Peaks II Second Derivative オプションまたは山印にローマ数字 2 が描かれたツールバーボタン 
をクリックします。
サンプルのデータセットがもつ多くのノイズによって、デフォルトの平滑化レベルと振幅の閾値では十分ではありません。PeakFit のもつ最大 100 ピークの制限は、あっというまに超えてしまいます。2次導関数による平滑化の結果は、下側グラフの上部プロットになります。
2.平滑化レベル（Sm%）の隣にある AI Expert ボタン をクリックします。AI Expert による平滑化レベルは、滑らかな 2次導関数曲線とデータを最上部にプロットします。
3.ベースライン付近に現れたノイズを消去するために、Amp% の値を 10% に設定します。
2次導関数は、ピークを最小値とします。稀にオリジナルデータで局所最大値ではないピークが、2次導関数による平滑化曲線では最小値とされる場合があります。
ここで、15 のピークが直接表示されていることに注意して下さい。2次導関数は、11 の局所最大値と 4つの隠れたピークをいっぺんに見つけ出しています。
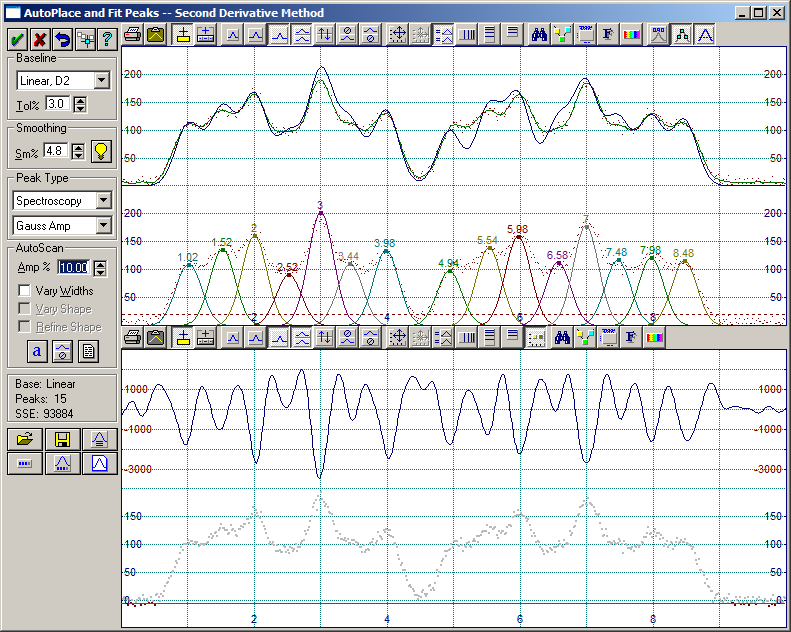
9．フィッティングの設定
フィッティングを開始する前に、その設定を確認しておきましょう。
1.Modify Peak Fit Preferences ボタン をクリックすると、オプション設定が表示されます。
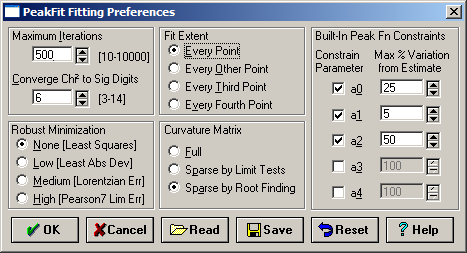
2.パラメータ a0、a1、a2 は、それぞれデフォルトで 25%、5%、50%に設定されています。
10．制約条件 (Constraint)
制約条件は相対値です。そして、最初のピーク位置にのみ適用されます（フィッティングが始まるとパラメータは変更されます）。制約条件が厳しすぎるか、あるいは最初の計算がこのパーセントをはみ出してしまう場合、フィッティングは制約条件内だけに制限されます。最適なフィッティングを行うには、このプロセスを何度も繰り返します。
11．数値フィッティング
このデータセットに対して、数値をフィッティングします。これで何の不都合もないときは、高速にフィッティングが行えます。組み込み関数に制約条件を与える方法では、結果を得るまでに時間がかかりますが、ほぼ最適な状態が得られます。
1.Fast Peak Fit with Numerical Update ボタン 
をクリックします。
フィッティングは収束するまで50回繰り返され、制約条件は 0〜1 の間で、インジケータとなるパラメータは 1つです。
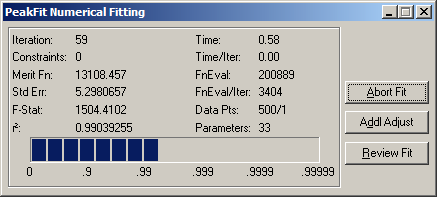
最終の r2 値は、残差によるフィッティングが 0.99087 だったの対して 0.99039 です。これは、パラメータの 1つが制約条件外に出るため、ほぼ最適な結果といえるでしょう。
2.Addl Adjust ボタンをクリックし、さらに Fast Peak Fit with Numerical Update ボタンをクリックしてフィッティングを再開します。
本例では、制約条件は最初のフィッティングから推定されます。なぜならこの方が正確で、制約条件のない場合が発生しても残差による方法と結果が一致するためです。
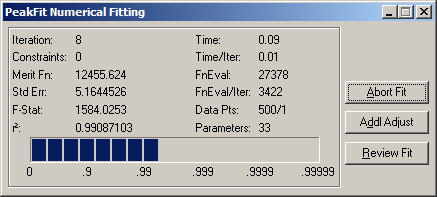
制約条件を広げたり無視することで、1回のフィッティングで最適な結果が得られる場合もあります。この場合、1つ以上のパラメータが制約条件なしあるいは小さな条件で非現実的な値をもち、間違ったフィッティングとなる危険性もあります。もっともよいのは、PeakFit のデフォルト設定の制約条件を用いてフィッティングを続けることです。もしフィッティング途中で非現実的な数値のピークが発生したら、制約条件をより厳しくします。最適な結果を得るためには、ピークの数値補正を行うことです。数値補正のマニュアル操作は、畳み込み（Deconvolution）法のところで述べます。
3.フィッティングが終了したら Review Fit をクリックします。
4.グラフを印刷したい場合は、ツールバーの中の Print ボタン 
をクリックします。
自動的に印刷プレビューが表示され、事前にフォントのサイズを設定する必要があります。
12．正規分布の誤差
最小2乗法によるフィッティングの場合、パラメータの標準誤差と信頼区間は正規誤差によって判別されます。これは、すなわち残差はガウス分布であることを意味しています。
1.標準残差プロットは Residuals をクリックすると表示されます。
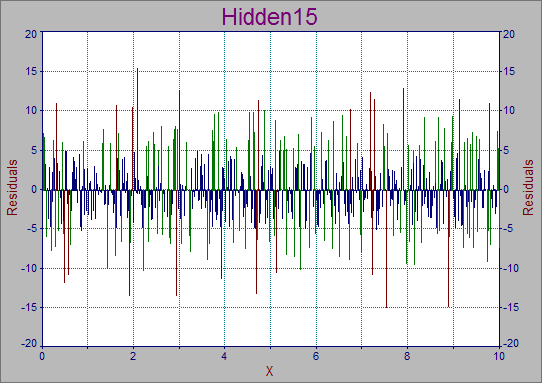
2.残差のヒストグラムを見るには、Display Residuals Distribution ボタン 
をクリックします。ガウス分布であることがわかります。
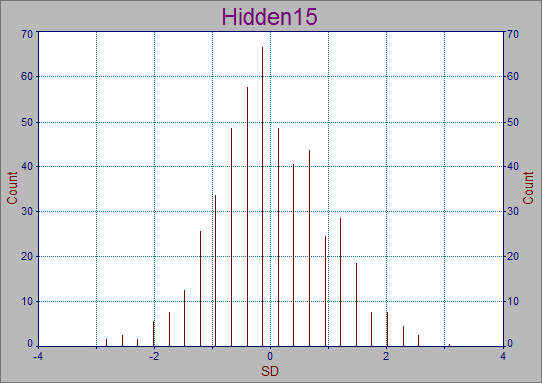
3.正規性を確かめるための境界線をみるには、Display Residuals in Stabilized Normal Probability Plot ボタン 
をクリックします。
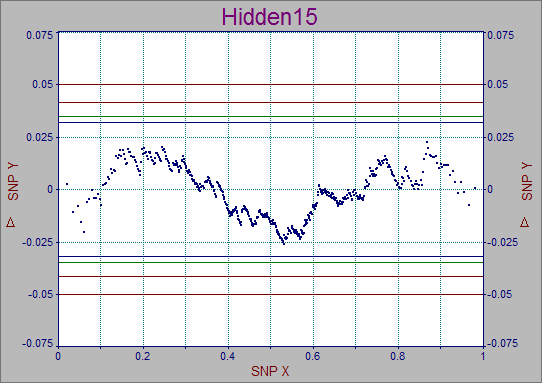
データ両サイドの4本の境界線は、90／95／99／99.9% 区間を表しています。99%区間は、100 ポイントのうち 1pポイントだけこの区間からはずれるということを表します。このフィッティングでは、すべての値が 90％の区間に収まっています。
4.残差ウィンドウを直接または Residuals ボタンをクリックして閉じます。OK ボタンを押してウィンドウを閉じると、設定が保存されます。
13．畳み込みによる自動フィッティング
1.AutoFit メニューの AutoFit Peaks III Deconvolution オプション、またはツールバーにある山印とローマ数字 3 のボタン 
をクリックします。
データをガウス型応答関数で畳み込んだとき、ピークの幅は狭く振幅が大きくなります。畳み込みは、ピークが隠れていたような局所最大値を見つけてくれます。畳み込んだデータは下側グラフの上部プロットになります。畳み込みは、応答関数の幅に非常に影響し（通常、最小のピーク幅よりさらに狭い）、フーリエノイズフィルタのレベルになります。
ガウス関数の畳み込みは、対象形のピークを持つデータ、とりわけガウス分布に近いデータに効果的です。すなわち、歪みをもつクロマトグラフやローレンツ型の曲線に適しています。
PeakFitは、最初の応答関数の幅の計算とデフォルトのノイズフィルタによって、ベースラインノイズである小さなピークと、目的とする15のピークを発見しています。
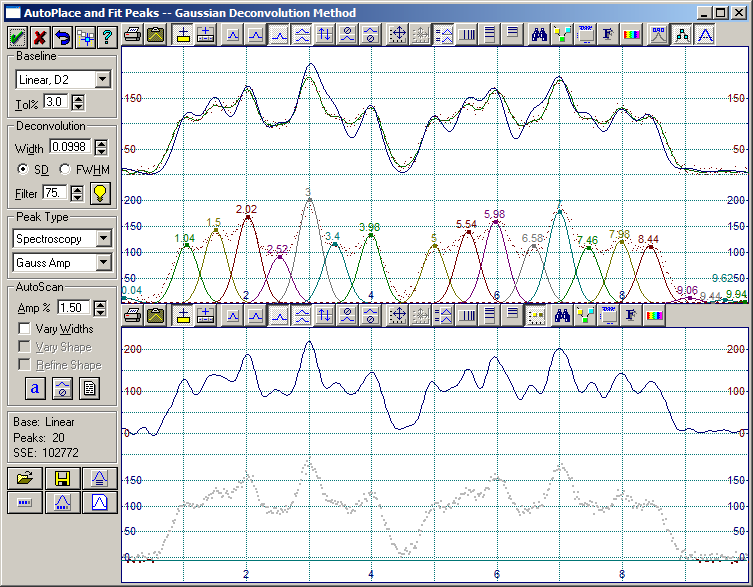
2.Filter レベルの隣にある AI Expert ボタンをクリックします。わずかな変化ですが、畳み込みデータには重要な変更が加えられます。
3.Amp% の値を 8% にして、ベースライン近辺のノイズであるピークを除去します。
11 の局所最大ピークと 4つの隠れたピークは、非常にはっきりと表示されています。
14．グラフ上での調整
パラメータの数値設定と同じように、自動設定ではなくグラフ上でマニュアル設定をすることもできます。
最初に振幅と中央値を示すアンカーポイントが表示されています。
1.ピークは、アンカーポイントをマウスの左クリックをし、ドラッグすることで位置とピークの高さを変えることができます。ドラッグをせずに左クリックを行うと、ピークの表示を ON／OFF するスイッチになります。この段階では、移動も表示 OFF にもしないで下さい。
ピークのない位置で左クリックをすると、新しくピークが追加されます。
2.マウスをピークの谷に置き（約 4.5、150 の位置）、マウスの左クリックを行うとピークが追加されます。
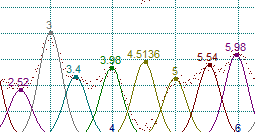
3.半値アンカーを使って1つ以上のピーク幅を修正
アンカーポイント上でマウスの右クリックをすると、ポップアップダイアログが表示されます。他のピークを選択すると、切り替わります。このダイアログを使って、ピークを削除したり、異なる関数を適用したりパラメータ値を修正したりすることができます。ロック（lockのチェックマーク）されたパラメータは、現在値に固定されフィッティングされません。共有（shareのチェックマーク）されたパラメータは、この位置で他のパラメータと値を共有します。
4.追加されたピークを右クリックします。
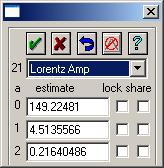
5.ピークを Lorentz Amp モデルに変更します。グラフがアップデートされ、パラメータの値も変更されます。
6.ピークを削除するには、Delete Peak アイコン 
をクリックします。
7.自動スキャンの設定を元に戻すには、Reset AutoScan ボタン 
をクリックします。ボタンは、コントロールパネルの上部にあります。
8.コントロールパネル下部にある Full Peak Fit with Graphical Update ボタン をクリックします。
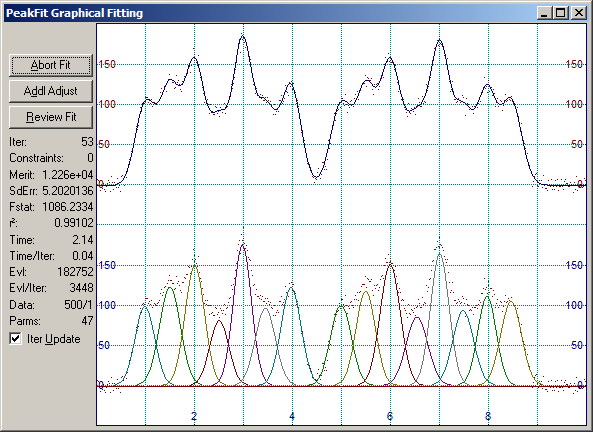
このチュートリアルで述べたように、制約条件に基づいてピークの幅が変更されます。この例では、パラメータの1つが制約条件まで到達しています。最適なフィッティングとするには、再度パラメータの値を変えてフィッティングを繰り返します。
9.Addl Adjust をクリックして Full Peak Fit with Graphical Update を選択します。
10.最適なフィッティングとなったかどうかは、もう一度フィッティングを行って確かめます。
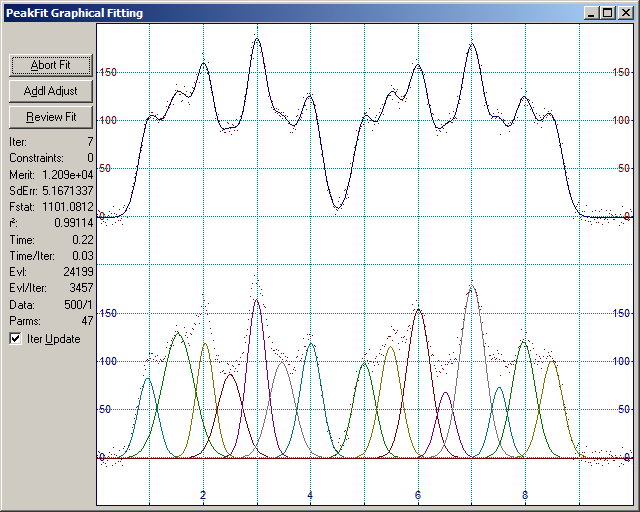
0.99114 の r2 値は、幅を固定してフィッティングしたときの値（0.99087）より高いことに注意して下さい。最小2乗法によるフィッティングは、15 のピークそれぞれに異なる幅を割り当てました。しかし、これは本当によいフィッティングなのでしょうか？ この幅を変えたフィッティングの F 統計量は、1101です。幅を固定した場合の F統計量は 1584 です。
11.Review Fit をクリックするとフィッティング結果が別のウィンドウにまとめられます。
ツールバーにある Copy ボタン 
をクリックすると、グラフをクリップボードまたはメタファイル、ビットマップなどにコピーすることができます。数値データは、スプレッドシートにコピーすることができます。
Review ダイアログにある Data オプションは、ポイント毎に推定値、残差、信頼区間、信頼限界を表示します。
12.Data ボタンをクリックして、データを見て下さい。
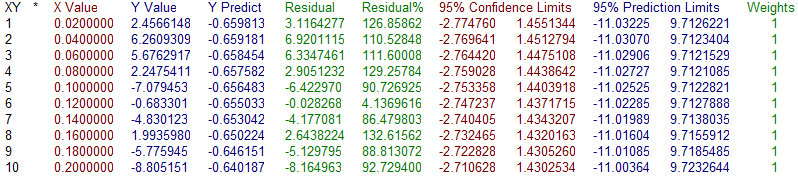
13.Data ボタンをもう一度クリックするか、直接ウィンドウを閉じて戻ります。
Eval オプションをクリックすると、フィッティングモデル同士を評価することができます。関数の評価に加え、1次および 2次導関数、累積および部分面積、フィッティングモデルの情報テーブル作成することができます。
14.Eval をクリックして、関数のタイプ、導関数、面積など、モデルの評価を行うことができます。これを使って 2種類の波形を計算し、比較することができます。またモデルの情報テーブルを作成することができます。
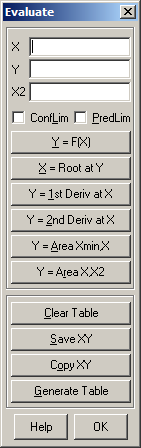
Export オプションを使って、元データと計算値、ピークなどを含んだ ASCII、Excel, Lotus、Quattro、SigmaPlot 形式ファイルを作成することができます。X 値の範囲と増分を設定し、自由にモデルを作成することができます。
15.実際にファイルを出力するには、Export ボタンをクリックし、ファイルの種類を選択してOK ボタンを押し、ファイル名を入力します。
16.OK ボタンをクリックしてウィンドウを閉じ、さらに OK（緑のチェックマーク）ボタンを押すと、現在の AutoFit オプションが保存されます。PeakFit を終了するには、メインウィンドウを閉じるか、 File メニューにある Exit コマンドをクリックします。