データ解析機能
回帰分析 (Curve Fitting)
回帰分析は Igor Pro の最も優れた解析機能のひとつです。
線形および一般的非線形回帰分析、一般 的な回帰組み込み関数、組み込み関数に対する自動初期値推定、多様なユーザー定義関数による回帰分析、格子状または多重列データとして独立変数をいくつも含む関数による回帰分析、波形または XYウェーブの部分領域への回帰分析、誤差の推定、重み付けのサポートなど様々な機能があります。
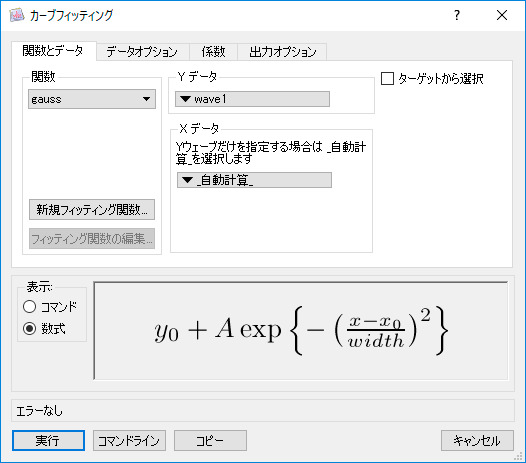
- 組み込み回帰関数
組み込み回帰関数には線形、多項式、サイン、指数、二重指数、ガウス、ローレンツ、ヒルの微分方程式、シグモイド、ログノーマル、ガウス 2D (2次元ガウスピーク)、多項式 2D (2次元多項式) があります。
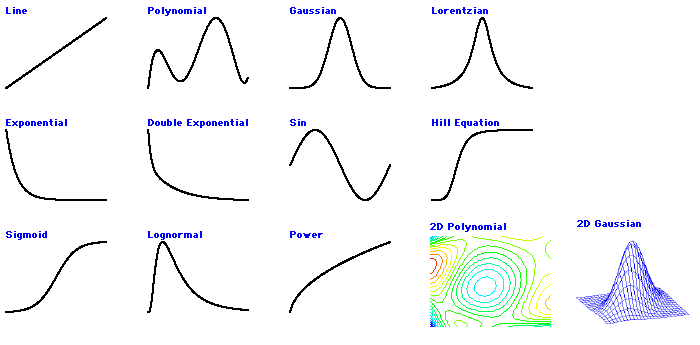
- gauss : ガウス曲線による回帰
- lor : ローレンツによる回帰
- exp_XOffset : 減衰指数曲線による回帰
- dblexp_XOffset : 2つの減衰指数曲線による回帰
- exp : 減衰指数曲線
- dblexp : 減衰指数曲線の和
- sin : シヌソイドによる回帰
- line : 直線による回帰
- poly n : n 項か次数 n-1 を伴う多項式による回帰
- HillEquation : Hill の方程式、S 字関数による回帰
- sigmoid : Hill の方程式と異なる形状をもつ S 字関数による回帰
- power : 累乗法による回帰
- lognormal : ログノーマルのピーク形状を回帰
- gauss2D : 2次元のガウス曲線を回帰
- poly2D n : 2次元における次数nの多項式による回帰
→関連:Igor Pro の定義済み組み込み関数
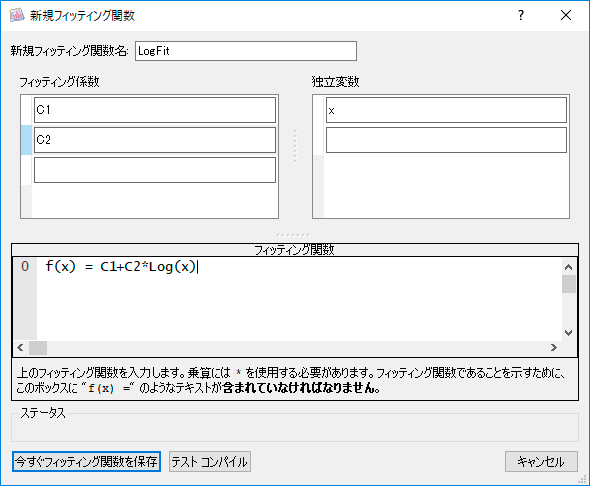
- ユーザー定義関数
ダイアログにユーザーが定義した回帰式を入力してユーザー定義関数を作成できます。
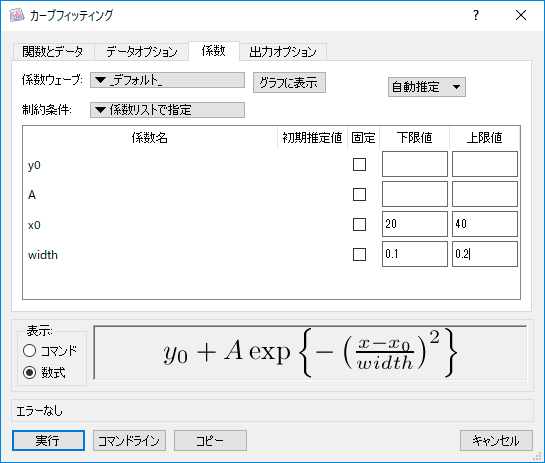
- 制限付き回帰
回帰分析ダイアログの「係数」タブにある制限付き回帰を可能にするメニュー。制限セクションに値を入力し、オーバーフロなどのエラーによる回帰の終了を防ぎます。
- 外部関数 (XFUNC)
外部関数 (XFUNC) は C または C++ で記述されています。XFUNC を作成するには、オプションの「Igor XOP Toolkit」および C/C++ コンパイラが必要です。WaveMetrics や他のユーザーから入手した XFUNC を使用する場合には、この Toolkit は必要ありません。
ピークの測定 (Peak Analysis)
ピーク測定の要は FindPeak コマンドです。このコマンドを使用してユーザー独自のピーク測定プロシージャを構築することもできます。また、WaveMetrics によって用意されているプロシージャを使用することもできます。
- ピークの検出 (Peak Finding)
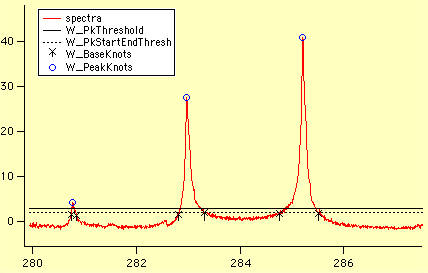
- BaseLine Removal
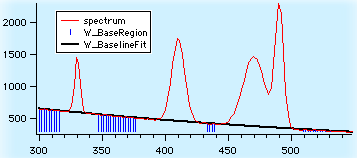
Multi-peak Fitting
Multi-peak fitting は、ピークタイプのデータを解析する場合に役に立つパッケージです。分光法やクロマトグラフィー、質量分析などから得られたデータに使用できます。Multi-peak fitting は、以下のような機能を含みます:
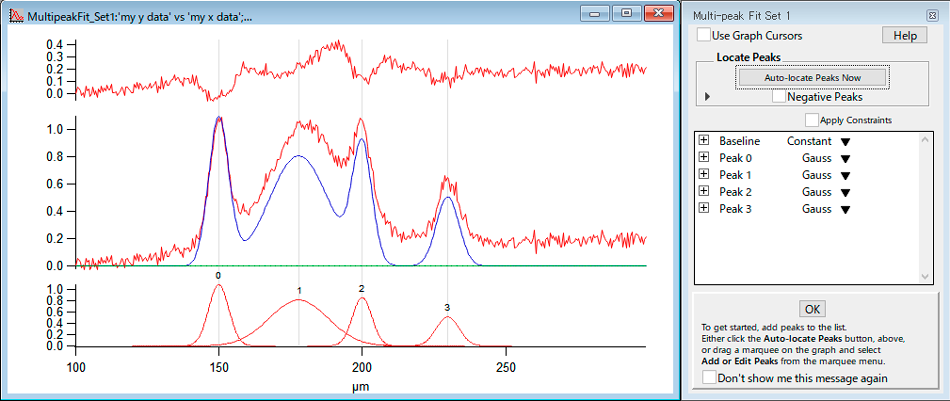
※Multi-peak Fit 2 の具体的な操作法につきましては、Multi-peak Fit ガイド ツアーをご覧ください。
- Gaussian、Lorenzian、Voigt、および、指数関数的に修正した Gaussian を含む、様々な異なるピーク形状
- 複数の重なり合ったピークをフィッティングする機能
- データセットの分析時に、異なるピーク形状を混合して使用する機能
- ピークの位置や高さ、幅の初期推定を生成する自動ピーク検出
- 正または負のピークとしてピークを扱う機能
- ベースラインまたはバックグラウンド関数の選択
- 手動でピーク検出を行う、または、自動検出されたピークのパラメータを変更するためのインタラクティブなエディター
- すべての処理をコントロールするインターフェイス
- ユーザ独自のプラグイン ピーク関数およびベースライン関数を記入可能にするモジュール アーキテクチャ
- ユーザ独自のコードから基本機能を使用することを可能にするプログラマ インターフェイス
信号処理 (Signal Processing)
信号処理 (Signal Processing) は、取得した生の時系列データを解析したり補正するために変換する科 学技術的手法です。例えば、スペクトル解析 (FFT 等を使用) やデジタルフィルタリングを使用して取得したデータを補正するような場合が含まれます。Igor は、非常に長い時系列データ (又は「ウェーブフォーム」) にも対応しているという点と、 豊富な組み込み信号処理コマンドをシンプルなダイアログを通じて利用できる点で、信号処理に使用するソフトウェアとしては最適なものです。また、Igor のプログラム言語を使えば、Igor のもつフーリエ変換等のパワーを活用することであらゆる種類のカスタム信号処理アルゴリズムを実装できます。
- フーリエ変換
Igor では高速フーリエ変換 (FFT) アルゴリズムを使用して、離散フーリエ変換 (DFT) の計算を行っています。FFT 操作関数は、信号の振幅と位相を検出するなどの大きな処理内の 1 ステップとして Igor プロシージャから呼出されます。Igor の FFT では素因数分解多次元アルゴリズムを使用しています。素因数分解を行うことによって、ほぼ任意の数のデータポイントを使用することができます。
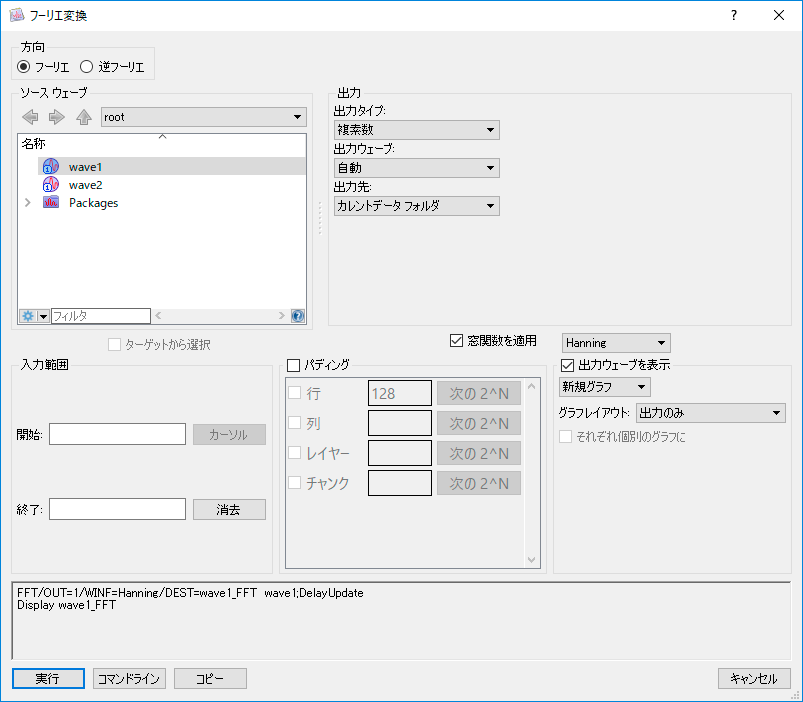
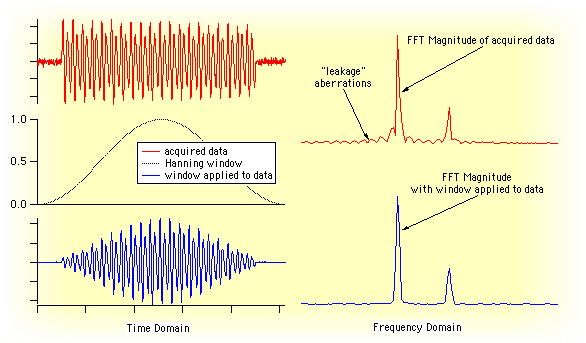
- スペクトルウィンドウ
FFT 計算は、データが何度も反復して入力されるとの仮定に基づいています。これは、データの初期値と最終値が異なる場合に重要な問題となります。この不連続性は、FFT 計算によって得られるスペクトルに狂いを生じさせます。データの末端をスムーズに接続するウィンドウィングにより、これらの狂いが取り除かれます。
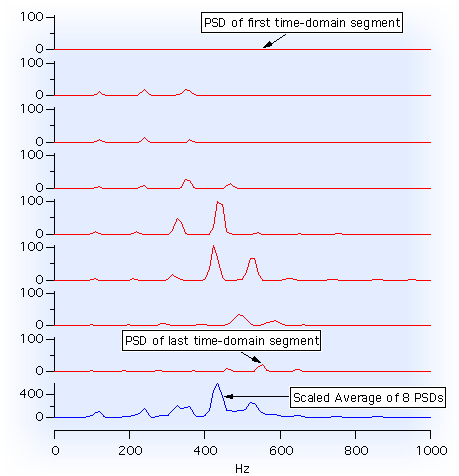
- パワースペクトル
「パワースペクトル」は、「どの周波数が信号のパワーを含んでいるのか?」という問いに答えを出します。答えは、周波数の関数としてパワー値の分布の形式であらわされます。この場合、「パワー」は、2信号の平均として考慮されます。周波数の領域では、FFT の振幅の2乗となります。パワースペクトルでは、全ての信号が一度に計算されます。言い換えると、時間信号の断片のピリオドグラムはすべて「パワースペクトル密度」の形式で平均化されます。
- Hilbert 変換
Hilbert 変換は、入力信号の位相を90度転換した時間領域信号を計算します。一次元の適用には、変調信号のエンベロープの計算および underdamped な線形・非線形システムでみられる幾何級数的に減衰する正弦曲線 (シヌソイド) の減衰率の測定が含まれます。
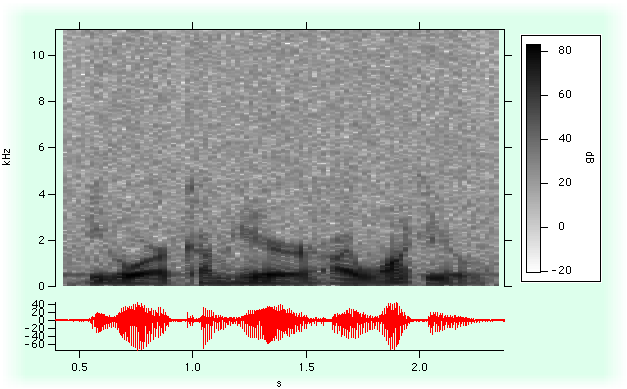
- 時間周波数解析
ある信号のフーリエスペクトル (又はパワースペクトル) を計算するとき、フーリエ変換に含まれるすべての位相情報はまとめて整理されてしまいます。信号にふくまれている周波数を調べることはできますが、その周波数が信号のどの部分に出現するかはわかりません。この問題の解決策のひとつに「短時間フーリエ変換」と呼ばれる方法があります。この方法では、スライドする一時ウィンドウを使用してフーリエスペクトルを計算します。ウィンドウの幅を調整することで、結果のスペクトルの時間分解能を決定することができます。
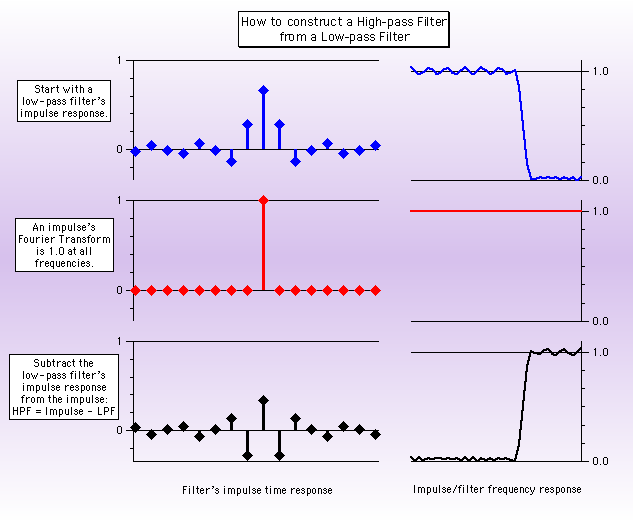
- デジタルフィルタリング
デジタルフィルタは、データが既にデジタル化されている場合に使用する本質的なツールです。データにデジタルフィルタを適用する理由には次のようなものがあります:不要な信号成分 (ノイズ) の削除。必要な信号成分の補正。特定の信号の検出。線形システムのシミュレーション (与えられた入力信号に対する出力信号の計算およびシステムの「変換関数」) 。デジタルフィルタには一般に FIR (Finite Impulse Response:有限インパルス応答) と IIR (Infinite Impulse Response:無限インパルス応答) フィルタの2種類があります。Igor は、主として Smooth 又は SmoothCustom コマンドによる時間領域畳み込みを利用した IFR デジタルフィルタリングを実装しています。SmoothCustom を使用した FIR フィルタ係数の設計は、Igor Filter Design Laboratory を利用すると便利です。IIR デジタルフィルタの設計とデータへの適用も IFDL で可能です。
- スムージング
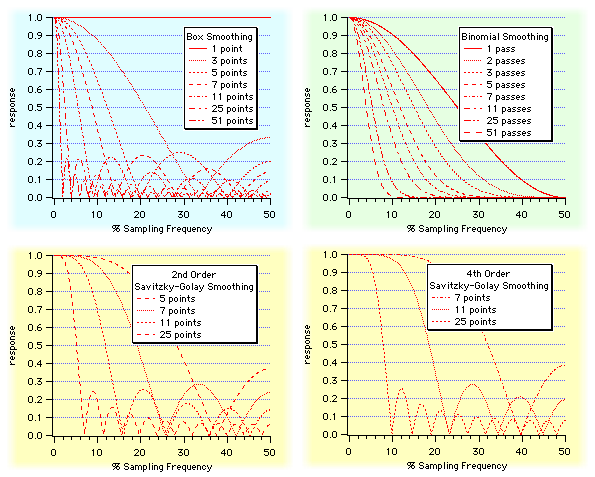
スムージングはデータのばらつきをなくすために使用するフィルタリング処理です。ノイズを消すために使用することもあります。Smooth 操作関数にはいくつかのスムージングアルゴリズムが内蔵されています。また、ユーザー独自のスムージング係数を使用することもできます。
- 2項スムージング
- Savitzky-Golay スムージング
- ボックススムージング
- カスタムスムージング係数
- 末端効果
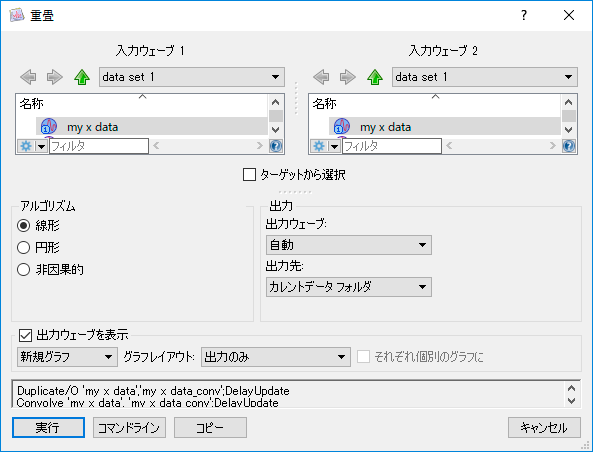
- 畳み込み (Convolution)
畳み込みを使用することで入力信号に対する線形システムの応答を計算できます。線形システムはそのインパルス応答によって定義されます。入力信号とインパルス応答の畳み込みが出力信号応答です。畳み込みは周波数領域におけるフィルタリングの時間領域での同等物です。Igor では Convolve 操作関数を使用して一般的な畳み込みが実装されています。
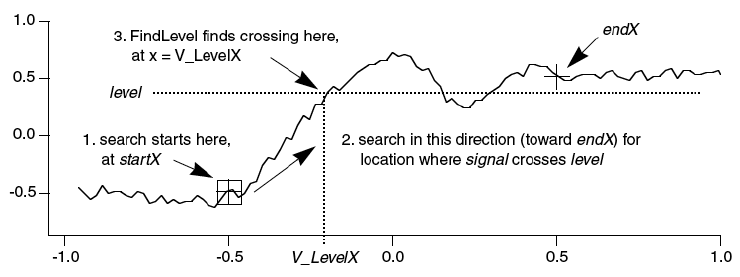
- レベルの検出
レベルの検出とは、与えられた Y 値を通る、または、与えられた Y 値に達するデータの X 座標を調べるプロセスです。これは「逆補間」と呼ばれることもあります。つまり、レベルの検出とは、「与えられた Y レベルに対応する X 値は何か」という質問に答えることです。この質問に対する Igor の答えには2種類あります。 そのひとつは Y データが単調に増減する Y 値のリストであると想定した場合の答えです。この場合は、Y 値に対応する X 値はひとつしかありません。検索の位置と方向は問題ではありませんから、このような場合には二分探索が最も適しています。もうひとつは、Y データが不規則に変化すると想定した場合の答です。この場合は、Y レベルを通る X 値が複数存在することがあります。返される X 値は、データの探求を開始する位置と方向によって異なります。
統計解析
Igor には、統計解析のための豊富な操作関数、関数、パッケージが装備されています。
1. 統計的検定
| StatsAngularDistanceTest | サンプルデータと 2 つもしくは複数のウェーブにそれぞれ含まれたサンプルの基準方向との間の角距離のノンパラメトリック検定を行います。 |
| StatsANOVA1Test | 一元配置の分散分析を行います。 |
| StatsANOVA2NRTest | 繰り返しのある二元配置分散分析を行います。 |
| StatsANOVA2RMTest | 繰り返しのない二元配置分散分析を行います。 |
| StatsChiTest | カイ二乗検定を行います。 |
| StatsCircularCorrelationTest | angular-angular または angular-liner の相関のパラメトリックまたはノンパラメトリック検定を行います。 |
| StatsCircularMeans | 多数の circular data の平均値の平均を計算します。 |
| StatsCircularMoments | 円形統計学的モーメントを計算します。 |
| StatsCircularTwoSampleTest | 角度の二次解析を行います。 |
| StatsCochranTest | Cochran の Q 検定を行います。 |
| StatsDunnettTest | ダネット検定を行います。 |
| StatsFriedmanTest | フリードマン検定を行います。 |
| StatsFTest | F 検定を行います。 |
| StatsHodgesAjneTest | Hodges-Ajne ノンパラメトリック検定を行います。 |
| StatsJBTest | Jarque-Bera 検定を行います。 |
| StatsKendallTauTest | ノンパラメトリック Mann-Kendall 検定を行います。 |
| StatsKSTest | Kolmogorov-Smirnov 検定を行います。 |
| StatsKWTest | ノンパラメトリック Kruskal-Wallis 検定を行います。 |
| StatsLinearCorrelationTest | wave の線形相関の検定を行います。 |
| StatsLinearRegression | wave の線形回帰分析を行います。 |
| StatsMultiCorrelationTest | 複数の相関係数に対して様々な検定を行います。(multiple comparisons with a control, multiple contrasts test and a Tukey-type multi comparison testing among the correlation coefficients) |
| StatsNPMCTest | ノンパラメトリックな多重比較検定を行います。(Dunn-Holland-Wolfe 検定、Student-Newman-Keuls 検定、Tukey-type (Nemenyi) multiple comparison 検定) |
| StatsNPNominalSRTest | ノンパラメトリックな一連の乱数検定を行います。 |
| StatsRankCorrelationTest | スピアマンの順位相関係数の有意性検定を行います。 |
| StatsResample | ブートストラップ法によりリサンプリングを行います。 |
| StatsScheffeTest | Scheffe 検定を行います。 |
| StatsSRTest | パラメトリックまたはノンパラメトリックな一連の乱数検定を行います。 |
| StatsTTest | 2 種類の T 検定を行います。1. 特定の値と分布平均の比較 2. wave 1 と wave 2 に格納された分布間の比較 |
| StatsTukeyTest | Tukey (HSD) / Newmann-Keels 検定を行います。 |
| StatsVariancesTest | Bartlett または Levene 検定を行います。 |
| StatsWatsonUSquaredTest | Watson のノンパラメトリック 2 標本 U 二乗検定を行います。 |
| StatsWatsonWilliamsTest | Watson-Williams 検定を行います。 |
| StatsWheelerWatsonTest | ノンパラメトリック Wheeler – Watson 検定を行います。 |
| StatsWilcoxonRankTest | ウィルコクソン・マン・ホイットニー検定を行います。 |
| StatsWRCorrelationTest | 重み付け順位相関検定を行います。 |
2. ノイズ関数
| 関数 | 分布 |
|---|---|
| binomialNoise | 二項分布 |
| enoise | 一様分布 |
| expnoise | 指数分布 |
| gammaNoise | ガンマ分布 |
| gnoise | ガウス分布 |
| hyperGNoise | 超幾何分布 |
| logNormalNoise | 対数正規分布 |
| poissonNoise | ポアソン分布 |
| StatsVonMisesNoise | Von Mises 分布 |
| wnoise | Two-parameter ワイブル分布 |
3. 確率分布関数
| Function | Distribution |
|---|---|
| StatsBetaPDF | ベータ分布 |
| StatsBinomialPDF | 二項分布 |
| StatsCauchyPDF | コーシー分布 |
| StatsChiPDF | カイ二乗分布 |
| StatsDExpPDF | 二重指数分布 |
| StatsErlangPDF | アーラン分布 |
| StatsErrorPDF | 誤差分布 |
| StatsEValuePDF | 極値分布 (type I, Gumbel) |
| StatsExpPDF | 指数分布 |
| StatsFPDF | F 分布 |
| StatsGammaPDF | ガンマ分布 |
| StatsGeometricPDF | 幾何分布 |
| StatsHyperGPDF | 超幾何分布 |
| StatsLogNormalPDF | 対数正規分布 |
| StatsMaxwellPDF | マクスウェル分布 |
| StatsNBinomialPDF | 負の二項分布 |
| StatsNCChiPDF | 非心カイ二乗分布 |
| StatsNCFPDF | 非心 F 分布 |
| StatsNCTPDF | 非心スチューデントの t 分布 |
| StatsNormalPDF | 正規分布 (Gaussian) |
| StatsParetoPDF | パレート分布 |
| StatsPoissonPDF | ポアソン分布 |
| StatsPowerPDF | べき分布 |
| StatsRayleighPDF | レーリー分布 |
| StatsRectangularPDF | 一様分布 |
| StatsStudentPDF | スチューデントの t 分布 |
| StatsTriangularPDF | 三角分布 |
| StatsVonMisesPDF | von-Mises 分布 |
| StatsWaldPDF | ワルド分布 |
| StatsWeibullPDF | ワイブル分布 |
4. 累積分布関数
| Function | Distribution |
|---|---|
| StatsBetaCDF | ベータ分布 |
| StatsBinomialCDF | 二項分布 |
| StatsCauchyCDF | コーシー分布 |
| StatsChiCDF | カイ二乗分布 |
| StatsCMSSDCDF | C (隣接間の差の二乗の平均) |
| StatsDExpCDF | 二重指数分布 |
| StatsErlangCDF | アーラン分布 |
| StatsEValueCDF | 極値分布 (type I, Gumbel) |
| StatsExpCDF | 指数分布 |
| StatsFCDF | F 分布 |
| StatsFriedmanCDF | フリードマン分布 |
| StatsGammaCDF | ガンマ分布 |
| StatsGeometricCDF | 幾何分布 |
| StatsHyperGCDF | 超幾何分布 |
| StatsKuiperCDF | カイパー分布 |
| StatsLogisticCDF | ロジスティック分布 |
| StatsLogNormalCDF | 対数正規分布 |
| StatsMaxwellCDF | マクスウェル分布 |
| StatsMooreCDF | Moore 分布 |
| StatsNBinomialCDF | 負の二項分布 |
| StatsNCFCDF | 非心 F 分布 |
| StatsNCTCDF | 非心スチューデントの t 分布 |
| StatsNormalCDF | 正規分布 (Gaussian) |
| StatsParetoCDF | パレート分布 |
| StatsPoissonCDF | ポアソン分布 |
| StatsPowerCDF | べき分布 |
| StatsQCDF | Q 分布 |
| StatsRayleighCDF | レーリー分布 |
| StatsRectangularCDF | 矩形分布 |
| StatsRunsCDF | Up and Down Runs |
| StatsSpearmanRhoCDF | スピアマンのρ分布 |
| StatsStudentCDF | スチューデントの t 分布 |
| StatsTopDownCDF | Top-down |
| StatsTriangularCDF | 三角分布 |
| StatsUSquaredCDF | ワトソンの U 二乗分布 |
| StatsVonMisesCDF | von-Mises 分布 |
| StatsWaldCDF | ワルド分布 |
| StatsWeibullCDF | ワイブル分布 |
5. 逆累積分布関数
| 関数 | 分布 |
|---|---|
| StatsInvBetaCDF | ベータ分布 |
| StatsInvBinomialCDF | 二項分布 |
| StatsInvCauchyCDF | コーシー分布 |
| StatsInvChiCDF | カイ二乗分布 |
| StatsInvCMSSDCDF | C (隣接間の差の二乗の平均) |
| StatsInvDExpCDF | 二重指数分布 |
| StatsInvEValueCDF | 極値分布 (type I, Gumbel) |
| StatsInvExpCDF | 指数分布 |
| StatsInvFCDF | F 分布 |
| StatsInvFriedmanCDF | フリードマン分布 |
| StatsInvGammaCDF | ガンマ分布 |
| StatsInvGeometricCDF | 幾何分布 |
| StatsInvKuiperCDF | カイパー分布 |
| StatsInvLogisticCDF | ロジスティック分布 |
| StatsInvLogNormalCDF | 対数正規分布 |
| StatsInvMaxwellCDF | マクスウェル分布 |
| StatsInvMooreCDF | Moore 分布 |
| StatsInvNBinomialCDF | 負の二項分布 |
| StatsInvNCFCDF | 非心 F 分布 |
| StatsInvNormalCDF | 正規分布 (Gaussian) |
| StatsInvParetoCDF | パレート分布 |
| StatsInvPoissonCDF | ポアソン分布 |
| StatsInvPowerCDF | べき分布 |
| StatsInvQCDF | Q 分布 |
| StatsInvQpCDF | 修正 Q 分布 |
| StatsInvRayleighCDF | レーリー分布 |
| StatsInvRectangularCDF | 矩形分布 |
| StatsInvSpearmanCDF | スピアマンのρ分布 |
| StatsInvStudentCDF | スチューデントの t 分布 |
| StatsInvTopDownCDF | Top-down 分布 |
| StatsInvTriangularCDF | 三角分布 |
| StatsInvUSquaredCDF | ワトソンの U 二乗分布 |
| StatsInvVonMisesCDF | von-Mises 分布 |
| StatsInvWeibullCDF | ワイブル分布 |
6. 一般的な目的のための操作および関数
| binomial | 二項係数を返します |
| binomialln | 二項係数の自然対数を返します |
| erf | 誤差関数 (error function) を返します |
| erfc | 余誤差関数を返します |
| inverseErf | 逆誤差関数を返します |
| inverseErfc | 逆余誤差関数を返します |
| Sort | 1 元配列をソートします |
| StatsCircularMoments | 角データの統計性を計算します |
| StatsCorrelation | ピアソンの相関係数を計算します |
| StatsMedian | 数値 wave のメディアン (中央値) を返します |
| StatsPermute | インプットエレメントの順番を変えます |
| StatsQuantiles | パーセンタイル (分位点) などを計算します |
| StatsResample | リサンプリング — ブートストラップ法 |
| StatsTrimmedMean | 分布の両端を取り除いた後、平均値を返します |
| WaveStats | 数値データの基本統計量を計算します |
7. 手法とパッケージ
| プロット関数 | |
|---|---|
| statsAutoCorrPlot() | ウェーブの自己相関をプロットします。 |
| statsBoxPlot() | ボックスプロットを作成します。 |
| statsPlotHistogram() | シンプルなヒストグラムプロットを作成します。 |
| statsPlotLag() | ラグプロットを作成します。 |
| statsProbPlot() | 確率プロットを作成します。 |
| WM_PlotBiHistogram() | bi-histogram プロットを作成します。 |
| 便利な関数 | |
|---|---|
| WM_2MeanConfidenceIntervals() | ふたつの母平均の信頼限界を計算します。 |
| WM_BernoulliCdf() | ベルヌーイ CDF を返します。 |
| WM_CIforPooledMean() | 統合平均の信頼区間を計算します。 |
| WM_CompareCorrelations() | ふたつの相関係数を比較します。 |
| WM_EstimateMinDetectableDiff() | ひとつのサンプルにおける最小検出差を計算します。 |
| WM_EstimateReqSampleSize() | 標本分散から必要なサンプルサイズを推定します。 |
| WM_EstimateReqSampleSize2() | 標本分散および検出力から必要なサンプルサイズを推定します。 |
| WM_EstimateSampleSizeForDif() | 平均間の特定の差を検出するために必要なサンプルサイズを計算します。 |
| WM_GetANOVA1Power() | 固定効果一元配置分散分析の検出力を計算します。 |
| WM_GetGeometricAverage() | 幾何平均を計算します。 |
| WM_GetHarmonicMean() | 調和平均を計算します。 |
| WM_GetPooledMean() | 同じ平均をもつ母集団のふたつの分散の統合平均を計算します。 |
| WM_GetPooledVariance() | ふたつ母集団の合併分散を計算します。 |
| WM_MCPointOnRegressionLines() | ふたつの線上の 2 点間の差を検定します。 |
| WM_MeanConfidenceInterval() | 平均値の回りの信頼区間を計算します。 |
| WM_OneTailStudentA() | スチューデント A の片側の結果を返します。 |
| WM_OneTailStudentT() | スチューデント T の片側の結果を返します。 |
| WM_RankForTies() | データに順位付けして、同順位の可能性を説明します。 |
| WM_RankLetterGradesWithTies() | 文字を順位づけします。 |
| WM_RegressionInversePrediction() | 線形回帰の逆予測を計算します。 |
| WM_VarianceConfidenceInterval() | 母分散の信頼区間を計算します。 |
| WM_WilcoxonPairedRanks() | ウィルコクソンの順位和検定における正または負の順位を計算します。 |
Wavemetrics 社サイト:「Statistical Analysis in Igor」
関数の解析
Igor Pro には、個々のデータポイントを操作するばかりではなく、関数について操作する機能も備わっています。
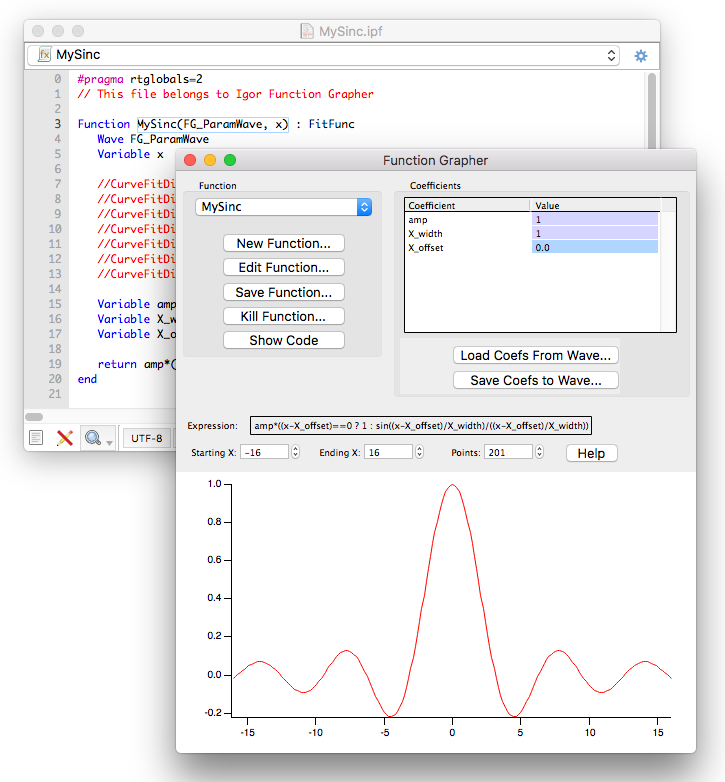
- 関数のプロット (Plotting of functions)
Igor を使うと簡単に関数のグラフを作成できます。 簡単な式の場合は、コマンドライン上で算術式を入力します。Igor のプログラミング言語を利用すると、 任意の複雑な非線形関数をユーザー定義関数として表現でき、これをグラフの作成に利用できます。
- 微分方程式 (Differential Equations)
常微分方程式の含まれる初期値問題の数値解を、IntegrateODE 操作関数を使用して計算することができます。ユーザー定義関数を作成して連立微分方程式を実装することも可能です。作成した微分方程式の解は、初期条件から前方 (あるいは後方) に順次解を求めていくか、独立変数を増加させて計算されます。
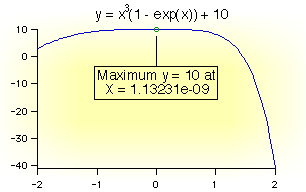
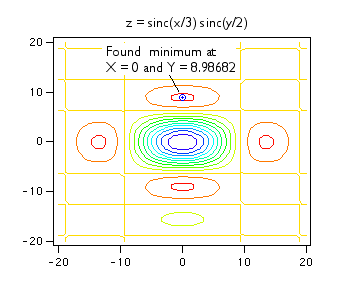
- 最適化 (Optimization)
関数の極大値又は極小値を求めるには Optimeze 操作関数を使用します。関数がある X 値をもち、そのときの Y 値がその近傍のすべての Y 値より小さい場合、この Y 値を極小値とみなします。
- 関数の根 (Function Roots)
Igor には、非線形関数、連立非線形関数、または実数係数を伴う多項式の根またはゼロを求める機能が用意されています。この機能は、FindRoots 操作関数を使用してコマンドライン上で実行します。
- 関数の積分 (Integration of Functions)
integrate1D 関数を使用して、ユーザー定義関数の数値積分を行うことができます。Integrate1D 関数は、台形、Romberg、ガウス求積の 3 種類の積分法をサポートしています。Integrate1D は、複素関数も処理できます。
