練習問題 (A Quick Warmup)
イントロダクション
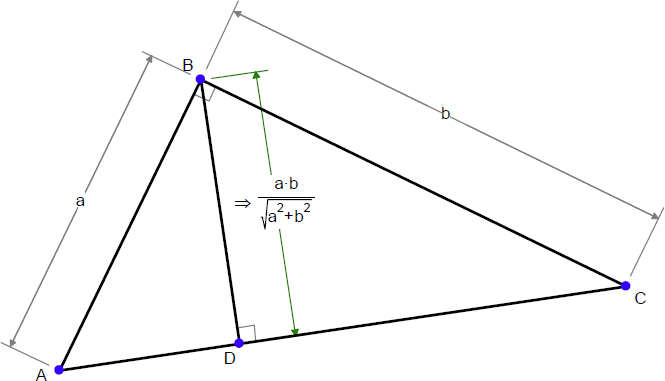
Geometry Expressions では、幾何学的図形から代数的表現を自動的に作成することができます。例えば、以下に示す図は、直角三角形の短い２辺の長さをそれぞれ a および b と指定したものです。このシステムで三角形の高さを数式で求めると以下のようになります
幾何学的演算を行うシステムが果たして幾何学の授業に役立つと言えるでしょうか？私ならイエスと答えるでしょう。この記事では、その答えが正当であることを実例を示しながら裏付けていきたいと思います。
1981年当時、私は研究助手としての生計を支えるのに数学の家庭教師を行っていました。その中の生徒の一人に、 “City and Guild” の電気工学の試験を勉強している人がいました。その試験の内容は、10年経ってもまったく変わっておらず、中には掛け算とべき乗の計算を対数表を使って行う問題も残っていました。私と同世代か年長の数学者なら、１より小さい数字が並んだ対数表を用いたこの一種独特の計算法を記憶している方もおられるでしょう。1982年には安価な小型電卓が出回るようになり、対数表を使った計算はまったく必要なくなりましたが、試験には依然としてこの問題が残されていました。対数表と逆対数表を使って調べていたのが、電卓の対数関数の取り扱いに変わったものの、生徒はこうした計算方法を引き続き学ぶ必要があったわけです。
テクノロジーは忌避するよりもむしろ積極的に取り入れるべきだと、私は考えています。
ウォーミングアップ
この記事の主要部分は、Geometry Expressions を使って具体的な幾何学的問題 (内接円と外接円) を検討していくものです。
ウォーミングアップとして、Geometry Expressions がいかに創造的数学の一過程となり得るかを示すいくつかの簡単な例題を検討することにしましょう。
例 1 ：一連の高さ
サンプルデータ：
それでは、イントロダクションで示した図を詳しく見てゆくことにしましょう
例１として、図形の作成方法について少し踏み込んで紹介します
使用するのは、３つのツールバーです。すなわち、描画ツールバーで図形を作成し、条件ツールバーで長さと角度を指定し、演算ツールバーで図形の高さを計測します。
まずはじめに、線分ツールを使用して図形を描画します：
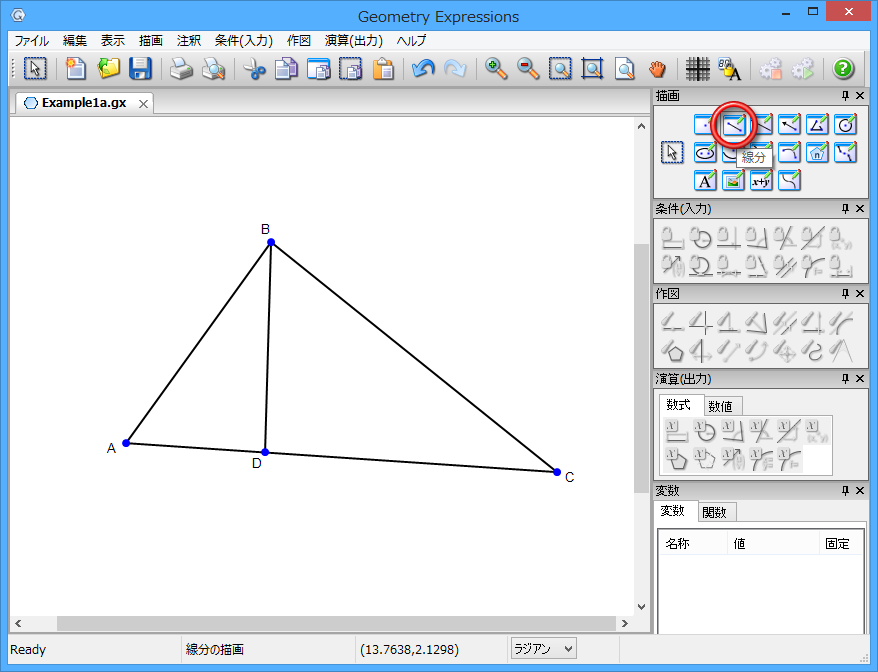
次に、垂直の条件を2箇所と、直線 AB と CD に対して距離/長さの条件を追加します：
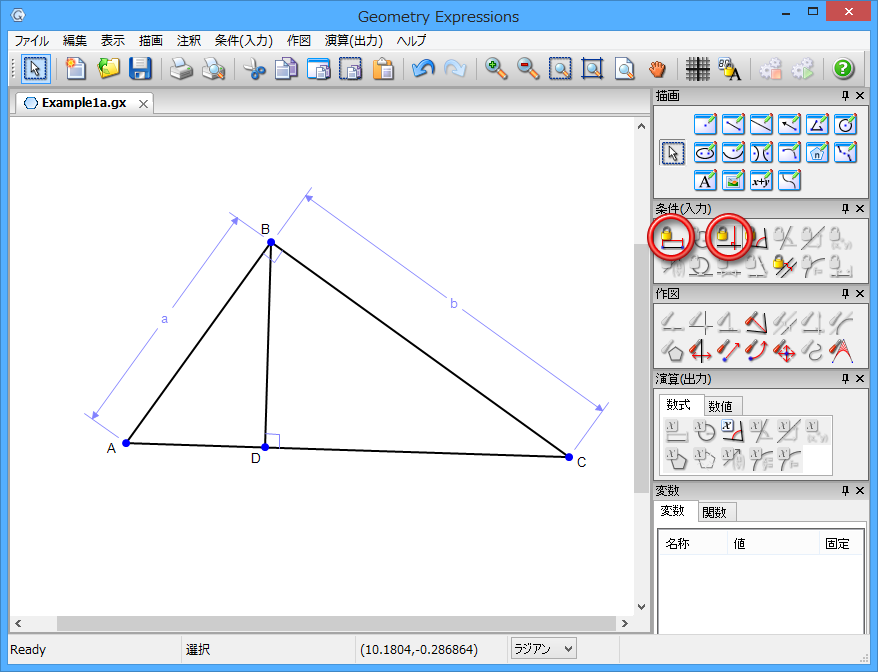
最後に、BD の長さを求めます。BD を選択したら、演算の数式にある距離/長さボタンをクリックします。
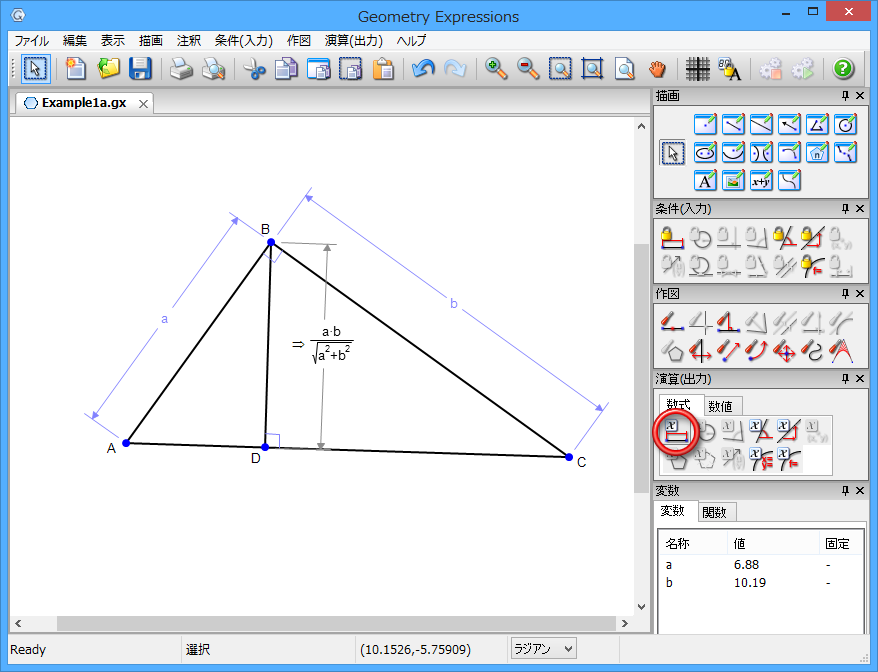
この高さの式が正しいことを証明できるでしょうか？（高さと三角形の面積の関係について考えてみましょう。）
次に、AD の長さを調べてみましょう：
|AD|/|BD| の比は幾つになるでしょうか？これによって、三角形 ABD と三角形 ABC の関係について何が分かるでしょうか？この関係を別な方法で定めることができるでしょうか？ (角度を考えてください) それによって、AD の式を証明できるでしょうか？
CD の長さは幾つになりますか？CD/BD の比は幾つになりますか？
三角形 ABD と BCD の関係はどうなるでしょうか？２つの三角形の斜辺の比は幾つになるでしょうか？
次に、ABD と BCD の内接円を作成してみましょう。(これらを作成するには、まずはじめに円を作成し、その後、円と三角形の該当する辺との間に、それぞれ、接線の条件を適用します。)
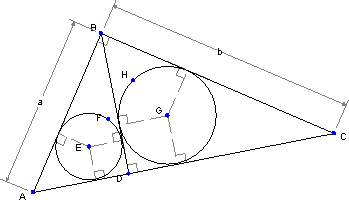
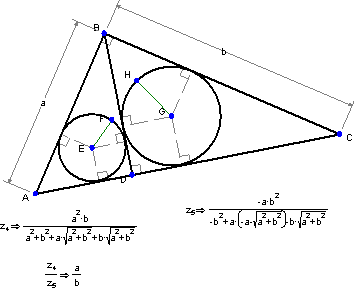
２つの内接円の半径の比は幾つになりますか？
この比は a/b であることが分かります。驚きではありませんか？
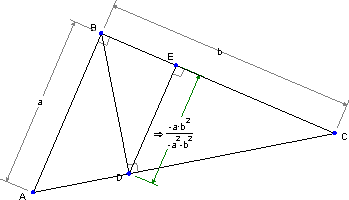
最初の図形に戻って、別の高さを作図してみましょう。
|DE|/|AB| の比は幾つになりますか？|DE| の式を証明できるでしょうか？
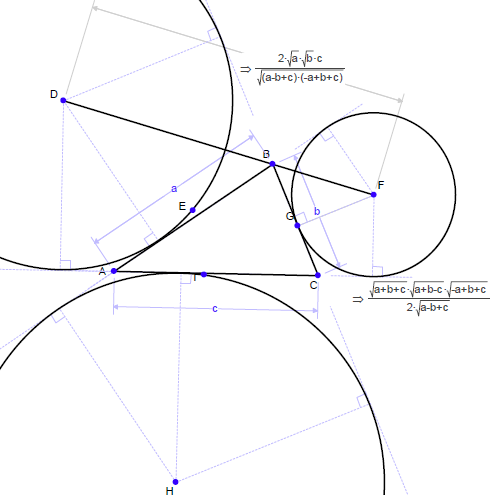
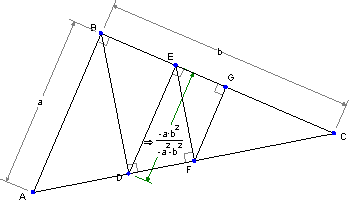
以下の図から、FG の長さを予測できるでしょうか？
例 2 ：角と円の関係
サンプルデータ：
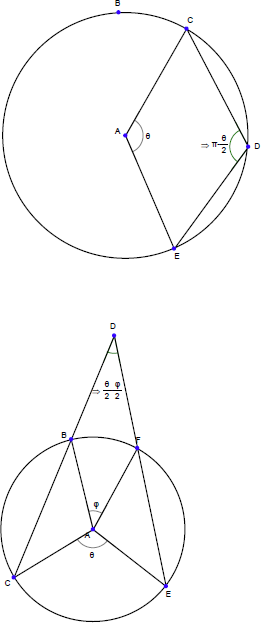
弦が円の中心角 θ をなすとき、その円周角はいくつになりますか？
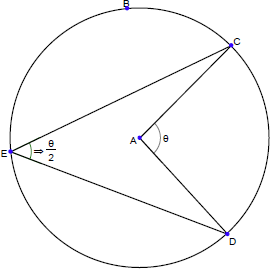
この結果を証明できるでしょうか？（ヒント：以下の図を使って、角度を埋めて行きます）
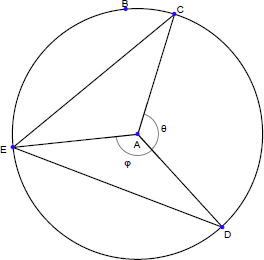
一連の図を示します。これを使って証明を組み立てることができますか？
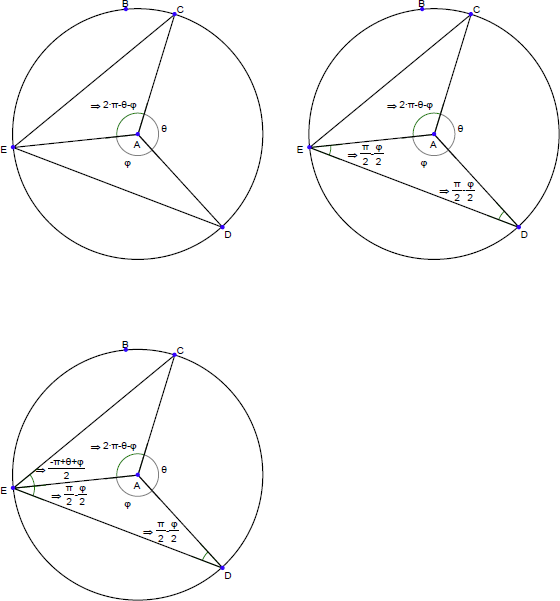
同様のアプローチに従って、以下の結果を証明してください：
例 3 ：三角測量
サンプルデータ：
Geometry Expressions には、主に幾何学的問題で登場する数式を操作するために特別に用意された独自の代数システムが装備されています。しかし、幾何学表現の分析を更に踏み込んで進めるには、より完備された代数システムにそれらをコピーして行います。Geometry Expressions では、数式を表示したり計算することができる様々なアプリケーションのインプットデータとして広く利用できる MathML 形式で数式をエクスポートすることができます。
この練習問題では、代数システムにコピーすることで分析を達成する事例を検討することにします。
三角測量を実行するコンピュータープログラムを記述するとします：三角形の底辺の長さと、底辺から頂点に向かう２つの角度が与えられると、プログラムはその頂点の座標を求めます。必要な数式は以下のように Geometry Expressions で生成されます：
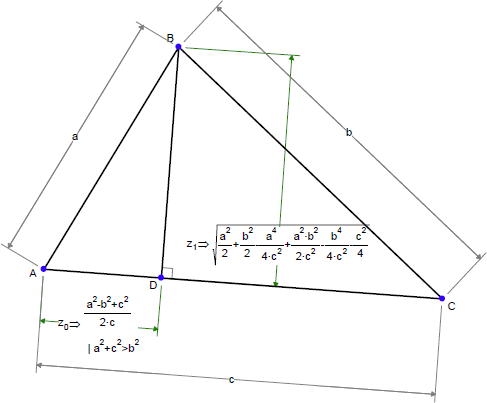
我々がコンピュータープログラムで知りたいのは、計算で求められる量の誤差が測定量 a および b の誤差と比例しているかということです。
a の誤差 δa による z0 の誤差は近似的に以下のようにあらわせます：
これは、z1 の誤差についても同様です。
量 
は、誤差の拡大鏡と考えることができます。
式 z0 を選択すると、その内容を代数システム (Maple、Mathematica など MathML を取り込むことができるよう設計されている任意のシステム) にコピー＆ペーストすることができます。ここでは、 Casio ClassPad Manager を使うことにします。代数システムに移ったら、a について微分を行い、誤差の拡大鏡に関する式を求めます：
z0 の誤差の拡大鏡は、a/c と単純な比になります。z1 に関する拡大鏡は、やや複雑なものになります。平方根の内部にある項を因数分解すると、その内容が明確になります：
a
a=b+c、または、b=a+c、c=a+b のとき、誤差項の分母がゼロなることがわかります。
幾何学的にこれらの条件を説明することができるでしょうか？
誤差項全体を幾何学的に説明することができるでしょうか？ヒント：分母と三角形の面積を比較します。分子を図の AD の距離と比較します。その長さがより厳密に分子と比例する距離を図中に作成できますか？
次のような問題も考えてもいいでしょう：三角測量に最適な形状とはどのようなものですか？問題を簡単にするために、三角形を二等辺三角形、かつ、a=b=x と仮定しましょう。また、底辺の長さは 1 であると仮定します。
これらの関数をグラフ化すると、x の値が大きいときに最初のドミネイトが、x の値が小さいときに第２のドミネイトがあるの観察できます。
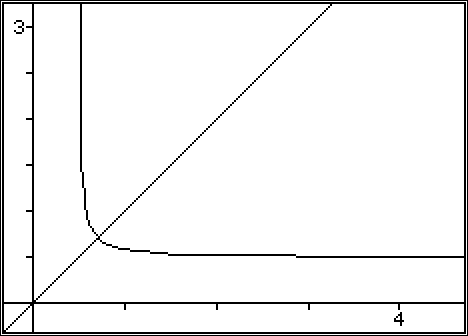
x の最適な値は、この２つが等しくなるときです：
このときの三角形の角度は幾つになりますか？
例 4 ：正三角形に外接する四角形
サンプルデータ：
Ross Honsberger 著 Mathematical Gems の 19-21 ページ (およびその他各所) には、次の定理があります：正三角形の角の１つが正方形の角の１つと重なるようにし、残りの２つの角はその対辺上になるよう、正方形の中に正三角形を描きます。これにより直角三角形が３つできます。このとき次の定理が導かれます：
いちばん大きな直角三角形の面積は、小さな２つの三角形の面積の和である。
Geometry Expressions を使って、互いに結びついた線分を選択して多角形を作図し、その後、その多角形の面積を測定することで、実際にこれらの面積を測定することができます。
以下の図は、上記定理の三角形の各面積を示すものです。
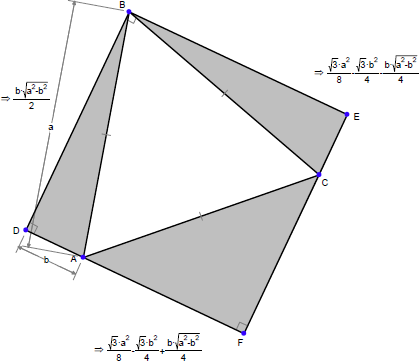
この図から定理を証明することができるでしょうか？
この図が正しいことを証明することができるでしょうか？
例 5 ：三角形の各辺の長さの三等分線に囲まれた六角形の面積
サンプルデータ：
三角形の頂点からその対辺を三等分する点に線をのばし、これらを交叉させると、影を付けた六角形ができます。
この面積は三角形 ABC の面積とどのような関係になるでしょうか？
この内容を証明できるでしょうか？
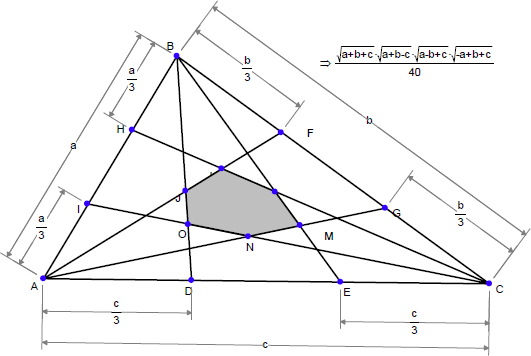
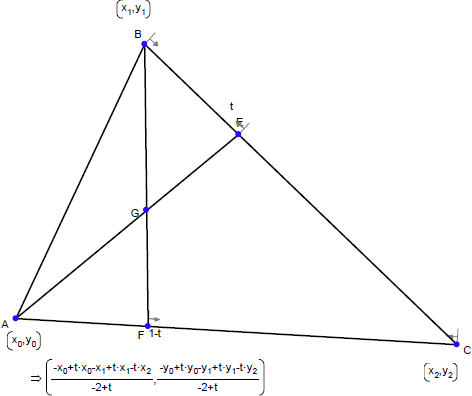
ひとつの方法は、E を AB 上の比例点 t、D を AC 上の比例点 t とする CE と BD の交点の位置をあらわす式を使うことです。t の値には 1/3 と 2/3 をそれぞれ使用して六角形の各点を求めます。
この情報を使って六角形の面積を証明することができますか？
この座標を証明することができますか？
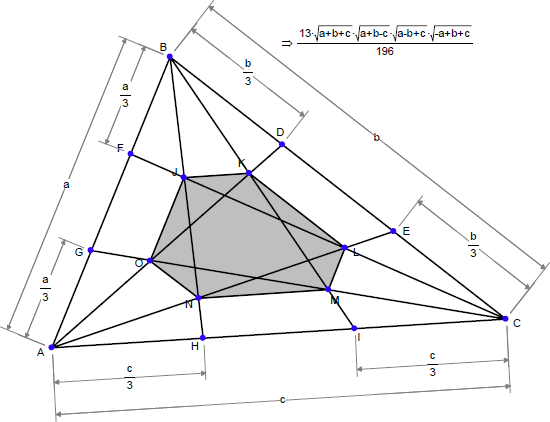
もうひとつの六角形の面積についてはいかがでしょうか？
内接円、外接円、および、関連事項の考察
引き続き、事例を続けることにしましょう。いずれも、内接円、外接円、傍接円、および、三角形の面積をテーマとするものです。
例 6 ：外接円の半径
サンプルデータ：
三角形の各辺の長さを a, b, c とするとき、その面積と外接円の半径を測定してください。
面積と半径はどのような関係になるでしょうか？
三角形が２つの辺とその間に挟まれた角で定義される場合、その面積はどうなるでしょうか？
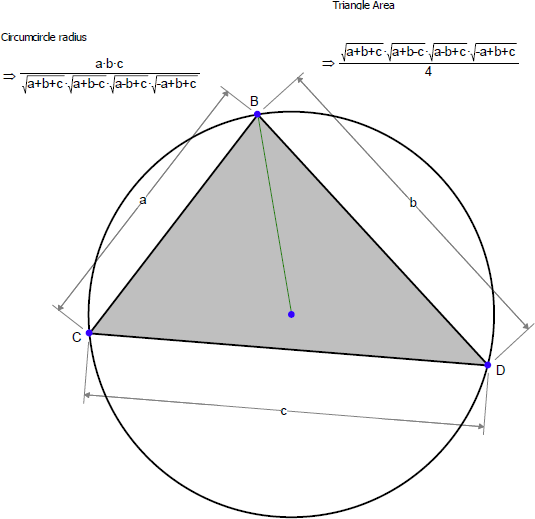
ここから、外接円の半径の式を角度を使って求めなさい：
Geometry Expressions では以下のようになっているはずです：
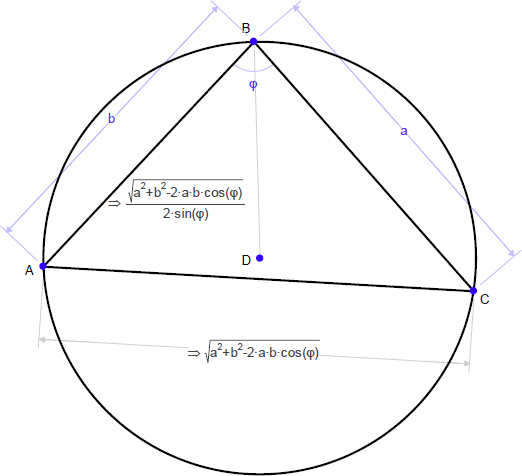
この式が Geometry Expressions を使わずに真であることを証明できるでしょうか？
ヒント：以下の図で |BC| の式を求めます。
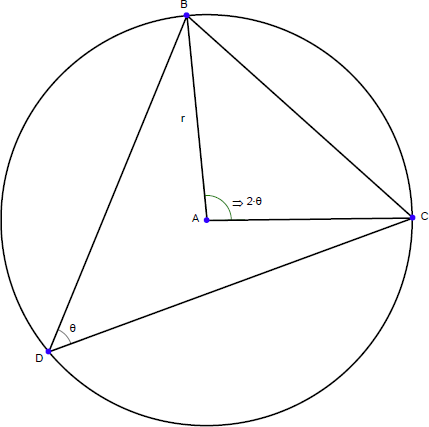
外接円の半径を R とし、三角形の角を A, B, C とし、その対辺の長さを a, b, c とします。この時点で、以下を証明できるはずです：
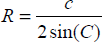
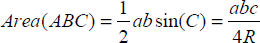
ゆえに
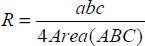
次に、R に関する最初の式を a, b, c を使って証明するのに必要なことは、Geometry Expressions で作成した三角形の面積の式を証明するだけです (さもなくば、証明なしに受け入れます)。
何の根拠もなしに、ものごとを受け入れようとは思いませんよね。
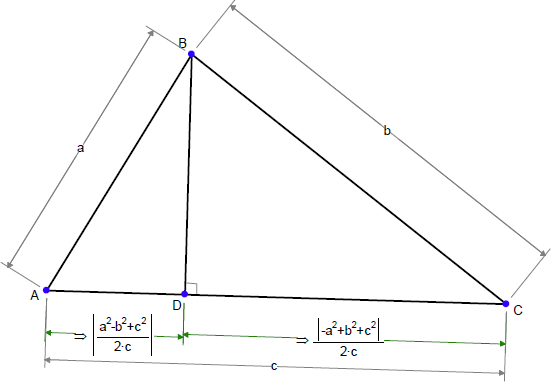
左図は、|AD| と |CD| の値を示したものです。
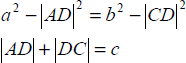
AD の式をお持ちの代数システムにコピーします。
次に、高さの二乗の式を作成します。これに c の二乗を掛けて、4 で割ることで、面積の二乗の式が作成されます：
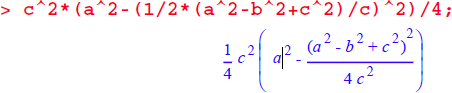
代数的な操作をこれに加えることで、次式が得られます。
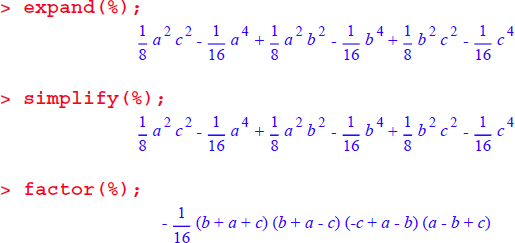
最後の練習問題として、三角形の頂点の座標を使って外接円の中心 (重心座標) を検討することにしましょう。
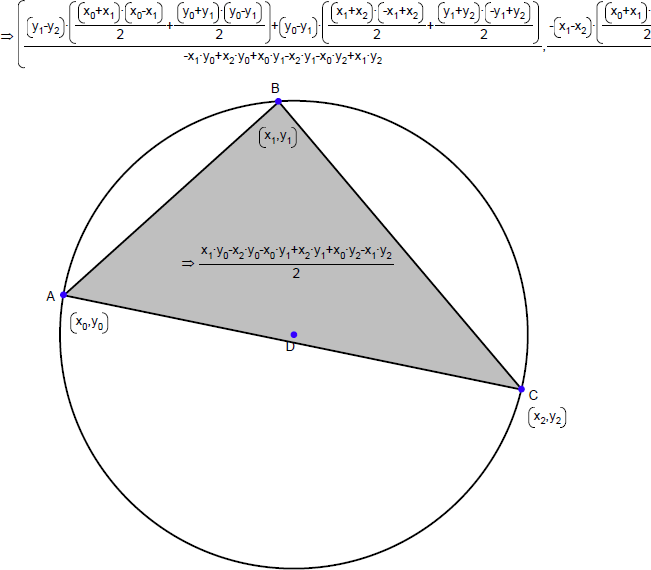
この式は、非常に複雑ですが、幾つかの要素に分解できます。式の中に面積が埋め込まれているのにお気づきでしょうか？
この内容をベクトルを使ってもっと簡単にあらわすことができますか？
例 7 ：内接円の半径
サンプルデータ：
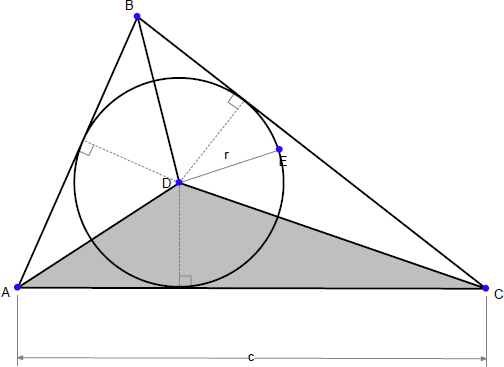
次に示すのは、内接円の半径の式です（良く知られた三角形の面積の公式も一緒に並べてあります）。
内接円の半径を面積を使ってあらわすことができますか？
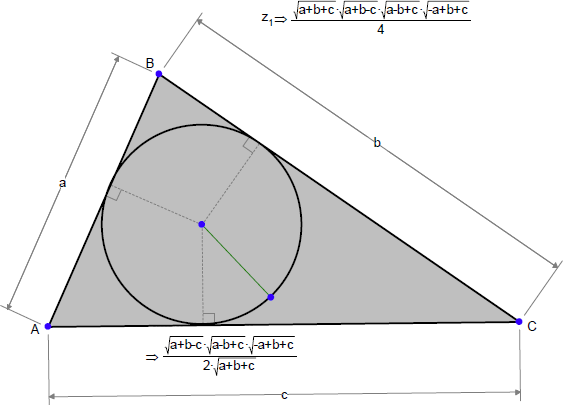
次に、この内容を Geometry Expressions を使わずに証明することができますか？
ヒント：三角形の影の付いた部分の面積を考えてください。
例 8 ：重心座標における内接円
サンプルデータ：
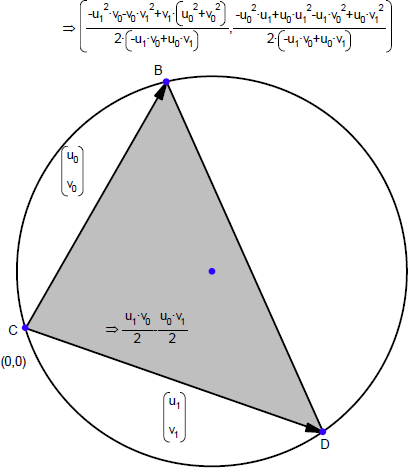
a=|BC|, b=|AC|, c=|AB| とし、A, B, C を点 A, B, C の位置ベクトルとするとき、内接円の中心は次式であらわすことができます：
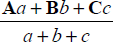
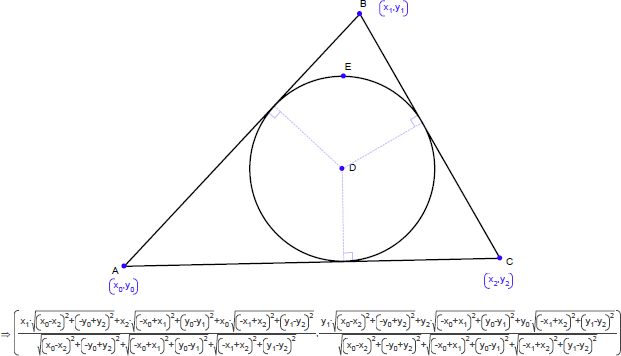
重心座標 (r, s, 1-r-s) を使って点を作成し、その点と三角形の３つの辺で定義される３つの三角形の面積を調べます（パラメータ値 r と s を r+s<1 を満たすように固定して、その点を三角形内部に配置してください）。
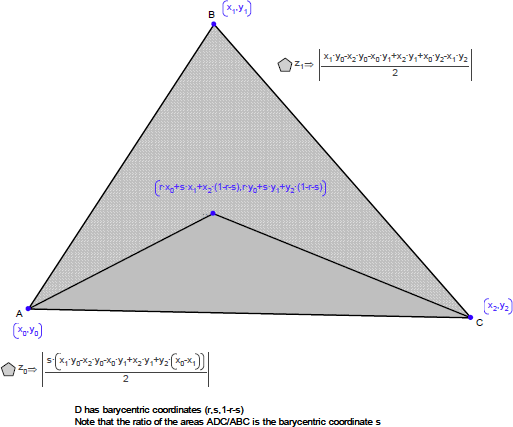
この面積と元の三角形の面積の比はいくつになるでしょうか？
この関係を使用して内心の重心座標の式を証明することができるでしょうか？
この関係を使用して、三角形の辺の長さで外心の重心座標をあらわすことができるでしょうか？
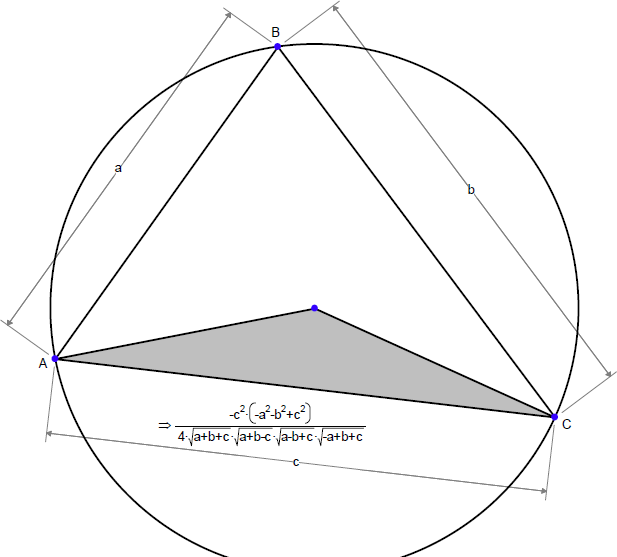
例 9：内接円と接する点は直線をどのように分割するか
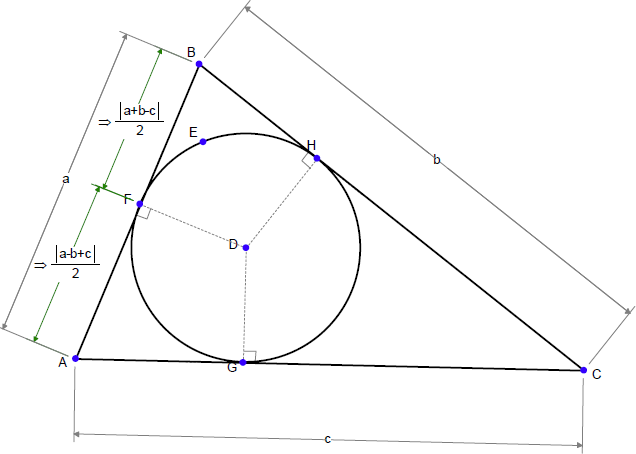
例 10 ：傍接円
サンプルデータ：
三角形の３つの傍接円は、三角形の３つの辺に接しますが、いずれも三角形の外側にあります：
この半径と三角形の面積との間の比はいくつですか？
三角形 ABF, ACF, BCF の面積を使って、この結果を証明することができるでしょうか？
残り２つの傍接円の半径は幾つになるでしょうか？
３つの傍接円と内接円の半径の積は幾つになるでしょうか？
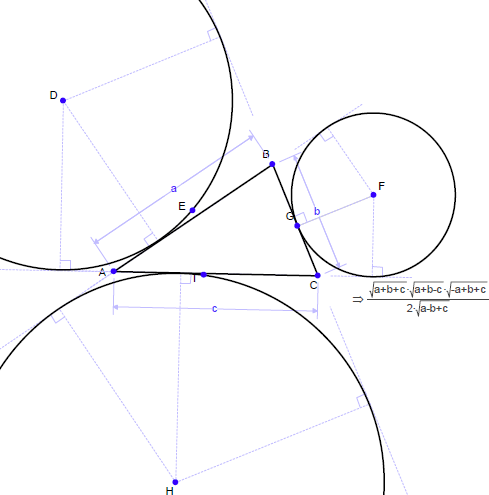
傍接円の２つの中心をつなげて三角形を調べてみます：
B が DF 上にあることを証明することができますか？（対称性を考えます）
その長さを証明することができますか？
