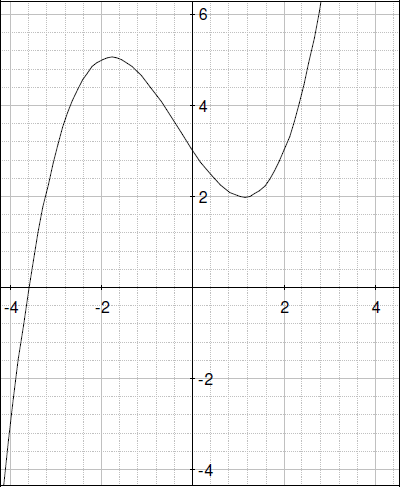
関数の垂直移動
代数2:計算の前段階(学習時間:50~80分)
| 学習目標 | このレッスンでは、関数に定数を加えた時の影響を理解するための基本的なアプローチを紹介します。 |
| 数学的目標 | ・関数に定数を加えた結果が垂直移動であることを理解します。 ・方程式の変化がグラフに与える影響、逆に垂直移動に関するかを理解します。 ・関数 y =x 2, y =1/x, y = sin (x) のグラフの形状といくつかの重要な特性を復習します。 |
| 技術目標 | 動かしながら調べるために、Geometry Expressions の関数機能と変数ツールを使うことに慣れていきます。 |
| 数学の前提知識 | ・関数というものが何で、次の3つの関数を理解している必要があります:
y =x 2, y =1/x, y = sin (x) ・正弦関数で使う弧度法(ラジアン)が十分に身についていなければなりません。 ・関数の表記を理解している必要があります:y=f (x) |
| 技術の前提知識 | Geometry Expressions の基本的な知識が必要です。これは、「単位円入門」のレッスン等で学習することができます。 |
| 準備するもの | ・学生1名、もしくは1組のペアの学生に対し、Geometry Expressions が動作するコンピューター1台 ・色鉛筆(あれば) |
概要 (教師用)
このユニットでは、3つの関数(親関数は y = x2, y =1/x, y = sin(x))を通じて、関数の変形を見ていきます。ここでは、視覚的に垂直移動を調べ、関数に定数をシンボリックに加算することで関係を分析します。垂直移動の理解は生徒にとっては簡単なので、各関数についての他の特性も見ることができ、同時にソフトウエアにも慣れることができます。対話的なソフトウエアの使用により、生徒は自分自身で容易に概念を理解することができると思われます。教師の役割は生徒を促し、脇道にそれないようにすることです。学生には、正確にパターンを理解したという確証が必要かもしれません。次に進む前に、特に漸近線と質問3の方程式を生徒が理解したということを確認したいと思うでしょう。
2つめのパートは、Geometry Expressions なしで行う必要がありますので、別の紙にコピーして生徒に渡し、生徒をコンピューターから離れさせます。ソフトエウアは考え方を発展させるすばらしい道具ですが、それをいつでも使うことを許せば、生徒が理解の欠如を隠す手段となります。彼らが自分で学習する概念を使用できること、また、コンピューターソフトだけでなく、数学を学ぶということが重要です。しかしながら、ソフトウエアはそれが可能です。そして後半では、ダイナミックなモデリング等のために、かなり広範囲に使われます。
色鉛筆は、グラフの変化を色分けするのに役に立ちます。これは、生徒が容易に理解できるためと、チェック/成績付けを容易にするために、推奨します。 クラスによっては、このレッスンは何度も繰り返す必要がある可能性もありますので、特定の生徒のグループに対しては、適宜、内容を修正したり、短くしたりする必要があります。
垂直移動・パートA
1. この時点で、アニメーションツールを使って見せても構いません。
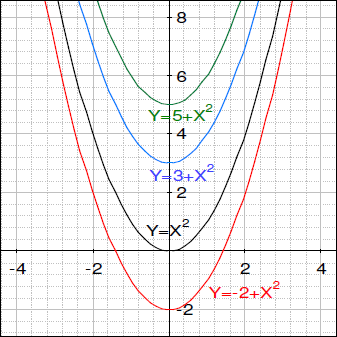
2. 答えはわずかに変化するかもしれません。グラフは、関数に加算される単位の数によって上がっていきます(垂直移動)。
それが負の数である場合、グラフは下へ移動していきます。
3.
A)
B) 原点を通る垂直線。
原点を通る水平線。
C) Y = 0; X = 0
これらを移動する前に、漸近線とその方程式について、生徒の理解を確認することが重要です。
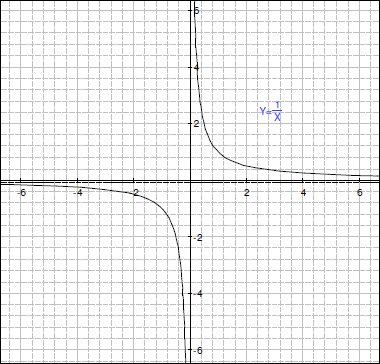
4.
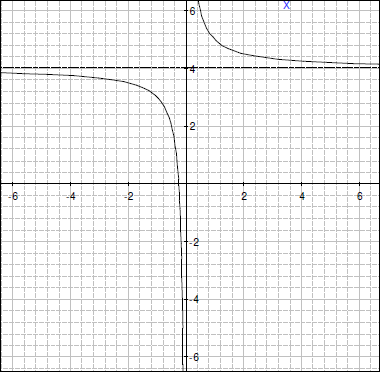
A) 2単位上にグラフを移しました(垂直移動)。
B) Y = 2
X = 0
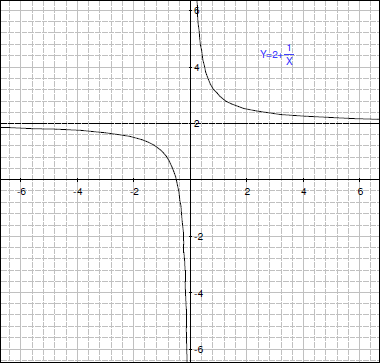
5.
A) 4単位上にグラフを移しました(垂直移動)。
B) Y = 4
X = 0
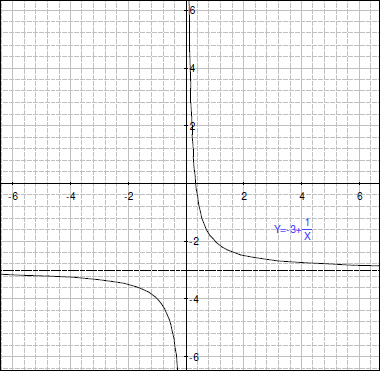
6.
A) 3単位下にグラフを移しました(垂直移動)。
B) Y = -3
X = 0
7.
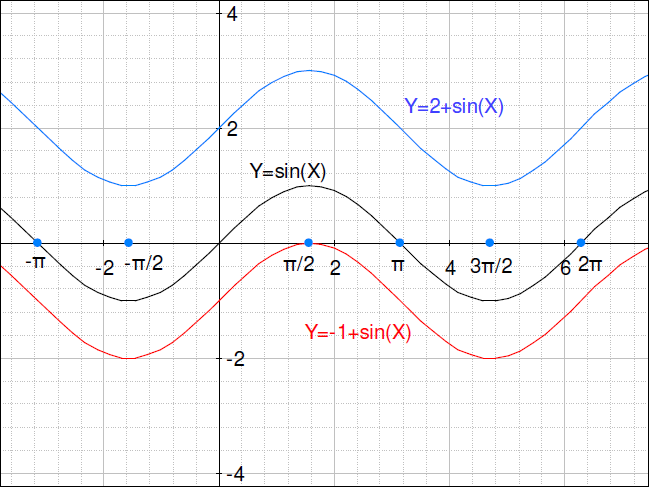
8. 関数に加算された数は、その数だけ垂直に関数を移動します。正数はグラフを上に、負数はグラフを下にスライドさせます。
教師が行うモデリング
自習のためにコンピューターから離れている生徒に、ホワイトボードなどで垂直移動を説明したいと思うかもしれません。一般的な問題は、学生が全体の図形を非常にラフに描くかもしれないということです。彼らが特定の点を見て各y値の移動量を追加する必要がある、という事実をモデル化して説明してください。特に、参照点として相対的な最大値と最小値を特定する例を与えて、曲線をモデル化することもできます。
垂直移動・パートB:自習
1-2)
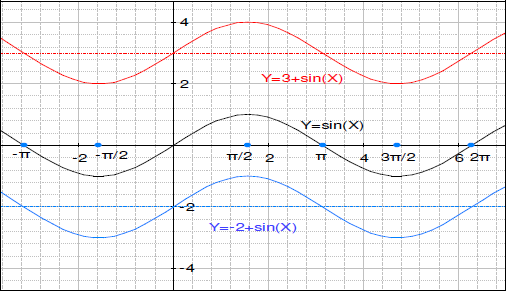
3-5)
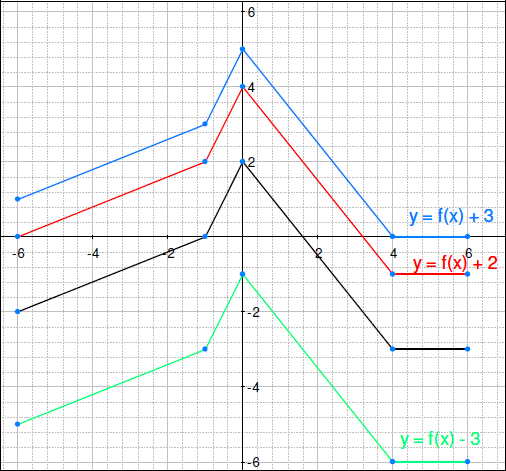
6-7)
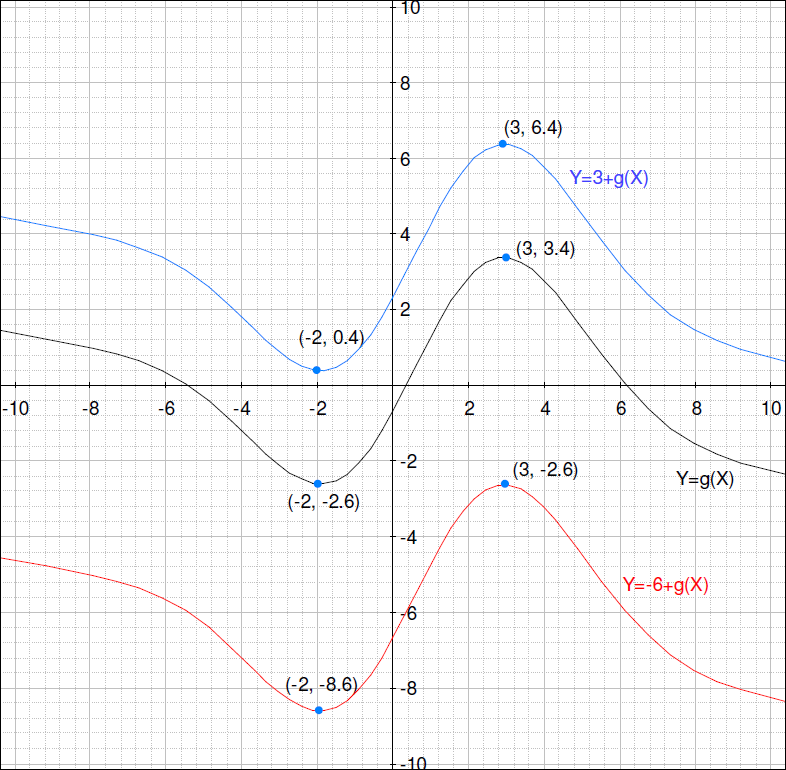
8)
j(x) = h(x) + 3
h(x) = j(x) + -3
9)
m(x) = k(x) + 3
k(x) = m(x) – 3
※ 次ページ以降が学生に配布する部分です。
垂直移動・パートA(生徒に配布する部分です。)
![]()
関数 y = x2 は、関数族の親で、そのグラフは放物線と呼ばれる形をしています。頂点、または最大値または最小値が放物線のキーポイントです。
1.以下のグラフを書き、定数を加えると、関数にどのようなことが起こるか、という大きなパターンを調査し、以下の質問に答えましょう。
Geometry Expressions の描画ツールの関数 ![]() を使って、
を使って、y = x^2 + c と入力します。この際、乗数を表現するために * 、指数を表現するために ^ を使う必要があります。次に、変数ツールパネルを使って c をハイライトして適当な数字を入力します。曲線をクリック、上下にドラッグ、また変数ツールパネルで c をハイライトしてスクロールバーをドラッグすることで、変数のより広い範囲でのグラフの変化を見ることができます。
| A) y=x2 | B) y=x2+3 |
| C) y=x2+5 | D) y=x2-2 |
2.そこに定数を加算したとき、グラフにどのようなことが起こりますか?負の数の場合 も含めて考えてください。
![]()
関数 y =1/x は関数族の親関数で、そのグラフは双曲線と呼ばれています。グラフは2本の漸近線を持っています。漸近線はグラフに近づきますが、決して接することのない線です。
3.
A) 以下に y =1/x を描きましょう。定規を使い、漸近線は点線で描きます。
B) 2つの漸近線の位置について説明してください。
原点を通る水平線。
C) 漸近線のそれぞれの方程式は:
Y =
X =
Geometry Expressions を使って y = 1 / x をグラフで示してください。以下に、この関数のグラフを作るため、いくつかの値を c に割り当てます。それぞれの場合において、”c” の値がグラフに与える影響を説明し、漸近線の方程式を記述してみましょう。さらに変数ツールパネルで c を選択し、いくつかの違う値がどのようにグラフに影響を与えるかを見ているために、スクロールバーをドラッグしてみましょう。
4. y =1/x +2
A) 値 “c” の影響は?
B) 漸近線の方程式

5. y =1/x +4
A) 値 “c” の影響は?
B) 漸近線の方程式

6. y =1/x –3
A) 値 “c” の影響は?
B) 漸近線の方程式

![]()
このユニットで調査する三番目の関数族は y = Sin (x) です。この関数は、パターンが一定の間隔で繰り返される周期関数であることを忘れてはいけません。正弦関数の場合、期間は 2π、または約 6.28 です。さらに、最大値 1、最小値 -1 で、直線 y =0(x 軸)中心軸を横切って振れます。
7.
A) y = sin (x) を描きましょう。
これまでの記憶を使って描くか、Geometry Expressions を使って描きます。
Geometry Expressions を使って、 y = sin (x) をグラフで示してください。プログラムをアジランモードに設定してください (編集/環境設定/計算/計算/角度モード→ラジアン)。指定された関数のグラフを作成するためには、c に異なる値を割り当てます(Geometry Expressions 上のグラフは π や 2π などのラベルは付いていないかもしれません)。どの場合も、中心軸は点線で描いてください。また、c の影響を調べるために、もう一度変数ツールパネルでスクロールバーを動かしてみましょう。
B) y=sin(x)+2
C) y=sin(x)-1
8.Geometry Expressions では、描画ツールの関数を使って y = f (x) のグラフを描きます。これは一般的な任意の関数です。ここでは y = f (x) + c のグラフです。c の値を変えるためには、変数ツールウインドウを使います。そこに定数を加算したとき、グラフにどのようなことが起こりますか?負の数の場合も含めて考えてください。
垂直移動・パートB(生徒に配布する部分です)
次の問題は、コンピューターや電卓を使わずに行わなければなりません。パート A を参照しながら進めてください。それぞれの問題では、目盛に注意し、特定のキーポイントを明示してください―あいまいなスケッチをしてはいけません。
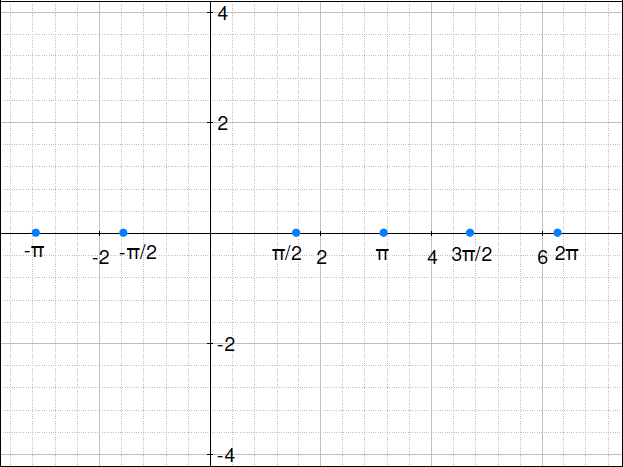
1.関数 y = sin (x) のグラフがあります。同じ軸で、y = sin (x) + 3 のグラフを描いてください。
2.上記の軸で、y = sin (x) – 2 を描いてください。そのグラフにラベルを付けるか、色分けしてください。
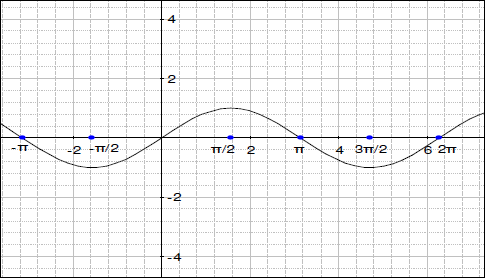
3. y =f (x) のグラフがあります。同じ軸で、y =f (x) + 2 のグラフを描いてください。グラフにラベルを付けるか、色分けしてください。
4.次に y =f (x) + 3 のグラフを描いてください。
5.次に、y =f (x) – 3 のグラフを描いてください。
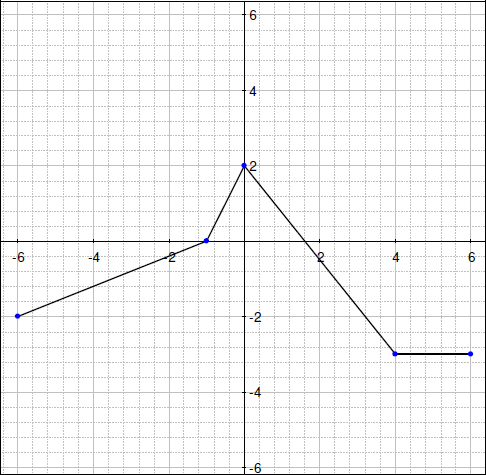
6. 関数 y = g (x) のグラフがあります。同じ軸で、y = g (x) + 3 のグラフを描いてください。
7.次に、上の方眼に y = g (x) – 6 のグラフを描いてください。グラフにラベルを付けるか、色分けしてください。
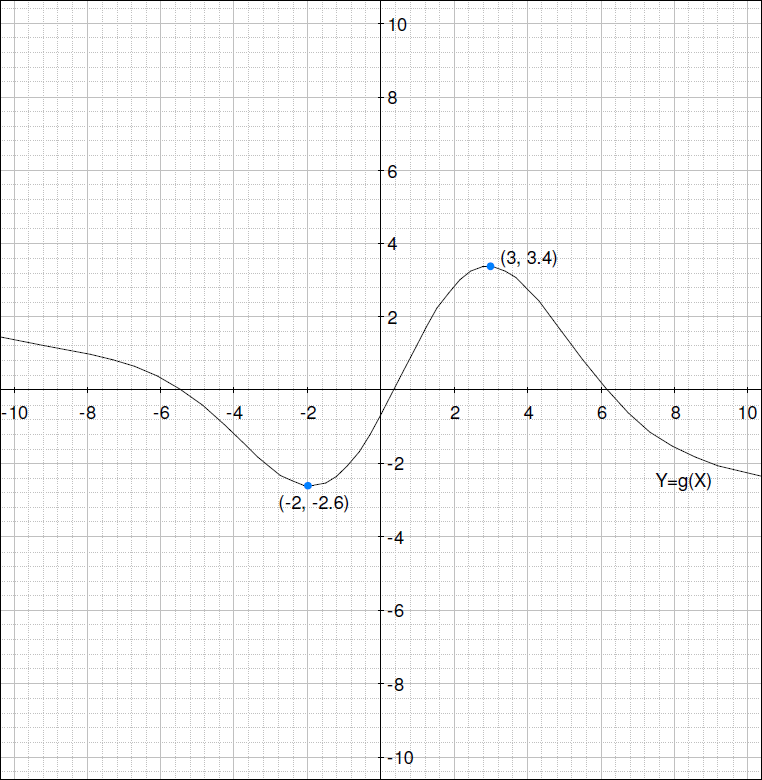
8.下に、お互いシンプルな関係性のある2つの関数 h (x) と j (x) のグラフがあります。1つは垂直移動です。下記の式の空欄を埋めて、その2つの関係性を書き出してみてください。
j(x) = h(x) + ______
h(x) = j(x) + ______
y=h(x)
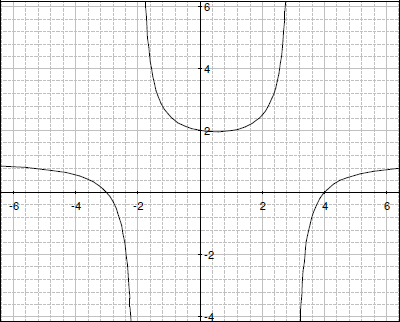
y=j(x)
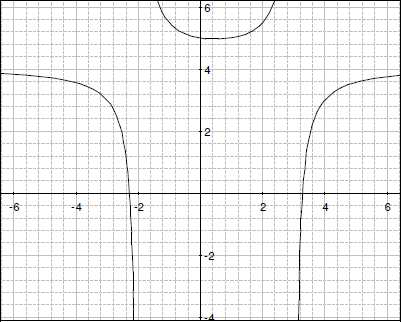
9.下に、お互いシンプルな関係性のある2つの関数 k (x) と m (x) のグラフがあります。2つの方程式を書いて、2つの方法で関係を書き出してみてください。
m(x) =
k(x) =
y=k(x)
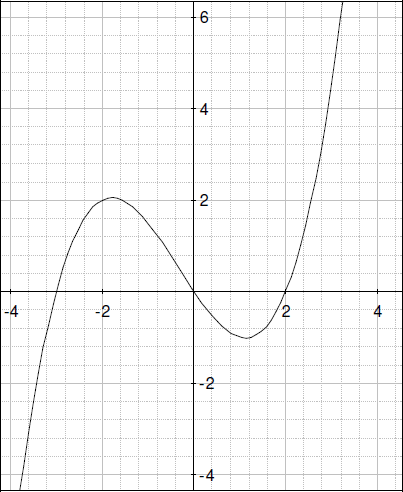
y=m(x)