基礎代数学から代数幾何学へ
基礎代数学から代数幾何学へ
このドキュメントでは、Geometry Expressions を使って、建物の面積のような簡単な問題から動的作図に至る高度なテーマをご紹介します。
(1)数式による入力と出力
(2)作図と条件
(3)微分
(4)軌跡と包絡線
(5)サンプル集
(6)動的作図
(1)数式による入力と出力
1. 三角形の面積
![]() サンプルデータ:
サンプルデータ:
以下に示す左上の図は、底辺が 6、高さが 4 の三角形です。この面積を学生に求めさせます。その結果、答えは 12 と返ってきます。この点を学生が動かすと、状況は動的に変化します。図形の変化に伴って領域も変化するわけです。しかし、入力内容と出力結果はいずれも数値です。数学的に証明される結果は何もありません。Geometry Expressions なら数学的証明を簡単に行うことができます。しかし、Geometry Expressions にできることはこれだけにとどまりません。
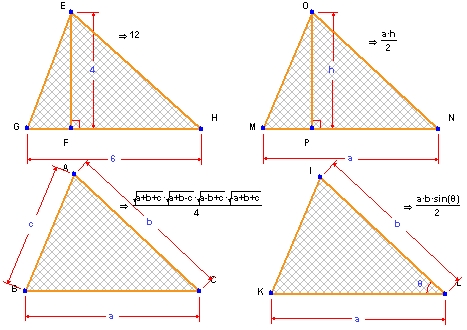
右上の図は、底辺の値に “a” を、高さに “h” を学生が入力したものです。この条件で面積を求めると、結果は a・h/2 と返ってきます。長さと角度について異なる内容 (数学用語で言えば異なる独立変数) を学生が入力すれば、返ってくる式も異なるものになります。もちろん、入力内容は、数値をとることもあれば、数式をとることもあります。従って、すべてが数値のものからすべてが数式のものまで、完全なフレキシビリティがあります。
2 建物の面積
![]() サンプルデータ:
サンプルデータ:
ここに紹介する面積の簡単な事例は、シカゴ大学学校数学プロジェクトの『代数学』 (Scott, Foresman) からの引用です。この中で生徒は、ある区画の端から特定の最小距離だけ離れたところに建物を配置するとき、その最大の大きさを求めるよう質問されます。この問題は Geometry Expressions を使うことで、以下に示すように簡単に行うことができます。
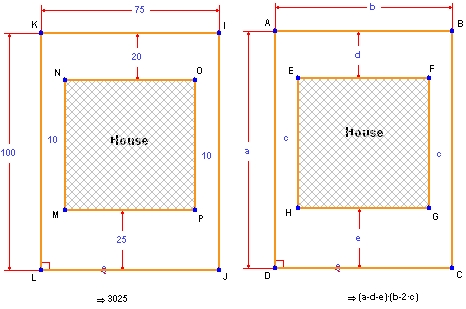
なお、Geometry Expressions で距離を記号として入力することは、ご覧のとおり数値を入力するのと何ら変わらずに簡単に行うことができる点に注目してください。入力が済んだら、建物の最大の面積を数式で求めることができます。
(2)作図と条件
3. 内接円の作図と条件の設定
4. 共通接線
3. 内接円の作図と条件の設定
Geometry Expressions では、作図と条件の両方がサポートされます。以下の図は、これら2つのアプローチの違いを分かりやすく説明する簡単な例を示したものです。上の図は、はじめに角の二等分線を2つ描画して内接円を作成します。その後、これら2つの直線の交点に点を配置し、この点を円の中心とします。そして、作成した円をその周囲が三角形の辺と接するところまでドラッグするか、点 G と一辺までの距離を数値的に測定し、得られた値を円の半径に設定します。以上の工程を経て求める円が作図されます。作図によるアプローチは、内接円とは何かをはじめて学ぶ人にとっては非常に役立つ手段です。しかし、内容が分かってくると、こうした作業が面倒に感じられるようになります。2つめの例は、円を描画したあと、その円と三角形の1辺を選択し、円と三角形の辺が接するように条件をあたえたものです (各辺について順番に繰り返す)。これだけで出来上がりです!
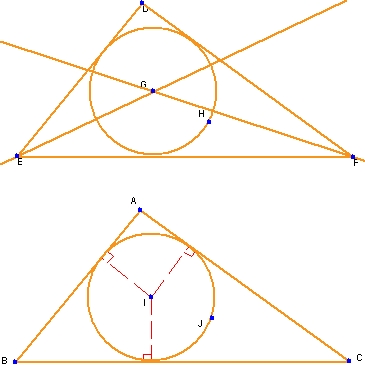
4. 共通接線
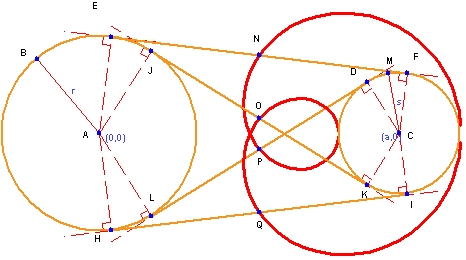
この例で検討するのは、2つの円の共通接線の中点の軌跡です。作成された図は一見非常に複雑なものに見えますが、Geometry Expressions なら作図と条件をうまく組み合わせることで非常に簡単に作成することができます。2つの円を描画したら、半径の条件に “r” と “s” をそれぞれ設定します。次に4つの共通接線を作成します。直線を単純に引き、2つの円それぞれに接するよう条件を与えます。次に、作図機能を使って、各直線に4つの中点を作成します。最後に、各中点を選択し、半径 r の変化に伴ってできる軌跡を求めます。
Geometry Expressions では、数値と数式のいずれも表現することができますので、公式をチェックするのに使うことも、定理を証明するのに使うこともできます。図形から期待されるアニメーション機能も備わっているので包絡線や軌跡を作図したり、あるいは、作成された曲線の実際の方程式を求めるといったユニークな機能を取り入れることもできます。ユーザーは、図形の作図と各種条件付けの両方を利用できるので、アプリケーションの多様性をフルに発揮させることができます。
(3)微分
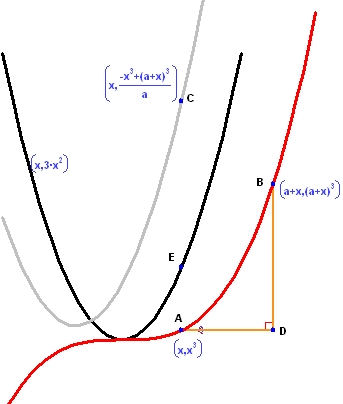
5. 3次関数の微分
関数 f(x) を x3 とします。2つの点の座標を (x,f(x)) と (x+a,f(x+a)) とし、Δy と Δx を示す直角三角形を描画します。作成したグラフは関数 f(x) (赤線) とその導関数 3x2 です。灰色であらわされている関数は (f(x+a) – f(x))/a です。ここで、パラメータ a を動かすと、Δy と Δx 、および、灰色のグラフの両方が変化するのを確認できます。パラメータ a の値を小さくするほど、灰色のグラフが黒のグラフに近づいてゆくのを確認できるはずです。すなわち、a がゼロに向かう極限を考える場合、点 B は点 A に向かって移動し、灰色のグラフ (導関数の近似式) は黒のグラフ (実際の導関数) に向かって移動することを、これであらわすことができます。
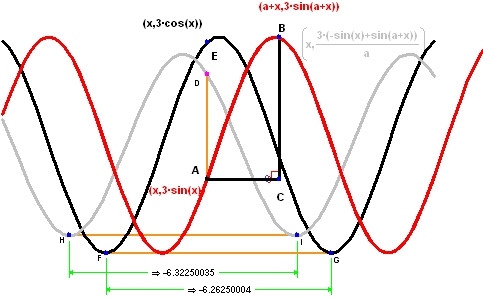
6. 正弦関数の微分
微分を極限で説明するもうひとつの例として、関数 3sin(x) を取り上げます。前回の例と同様に、関数 3sin(x) の導関数 (3cos(x)) とその近似式 (灰色で表示) を描画します。ここでも、パラメータ a をゼロに向けて動かしてゆくと、灰色の曲線が実際の導関数 (黒の曲線) に向かって移動します。初歩の学生にとって、この導関数の近似式は元の関数を縮尺し、平行移動しただけにしか見えないかもしれませんが、実際はそうではありません。このことを証明するために、各グラフで連続してあらわれる最小値間の距離が同一ではないということをハイライトで表示してあります。
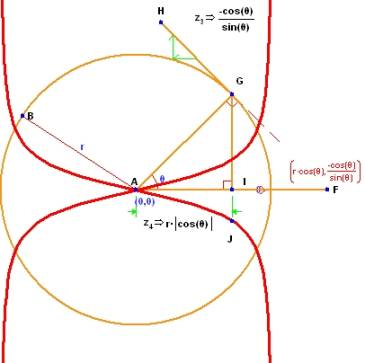
7. 円と傾き
微分に関する最後の例として、1つの円を示し、曲線に対する接線の傾きを使って導関数を説明します。AG と水平線 AF のなす角を θ とします。線分 GH を描画し、それが円の接線となる条件を与えます。次に、この直線の傾きを演算し、–cos(θ)/sin(θ) を求めます。最後に、この傾きのグラフを θ の関数として描画します。θ が変化するにつれて、点 G がこの円を移動し、点 J がその傾きの値を示します。
(4)軌跡と包絡線
8. ちょっと変わった円の軌跡
9. ちょっと変わった円の軌跡と包絡線
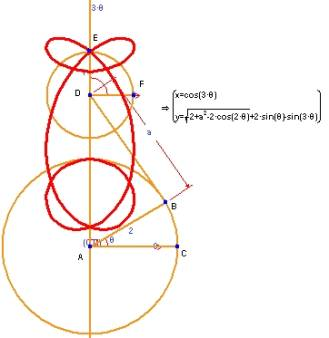
8. ちょっと変わった円の軌跡
この例では、中心を A とする半径 2 の円周上に点 B を配置します。AB と水平線 AC がなす角を θ とします。θ をこのアニメーションのパラメータとします。点 D が A を通過する垂直線上に配置されるよう条件を与え、BD の距離を a とします。D を中心とする単位円の円周上に点 E を配置し、DE と水平線 DF がなす角を 3θ とします。これにより、θ の変化に応じて、点 D は垂直線を上下にスライドし、点 E は単位円の周囲を点 B が中心を A とする円の周囲を回転する 3倍の速さで回転することになります。赤で示したのは、点 E が描く軌跡です。なお、この軌跡に加えて、Geometry Expressions でそのパラメトリック方程式を θ と a を使って求めている点も注目してください。
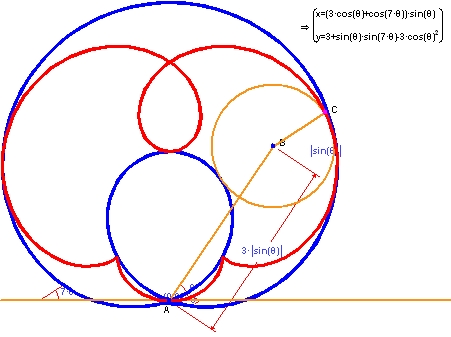
9. ちょっと変わった円の軌跡と包絡線
この図では、点 B を中心とする円の周囲に点 C を配置しています。ただし、AB と水平線がなす角を θ とし、AB の長さを 3 sinθ、円の半径を sinθ としている点に注意してください。これにより、θ の変化に応じて、円の半径と点 A との距離の両方が変化することになります。赤の曲線は点 C の軌跡、青の曲線はこの円の包絡線です。なお、ここでは赤の曲線のパラメトリック方程式を求め、その数式が出力されている点についても注目してください。
(5)サンプル集
10. スライドベクトル
11. 関数の鏡映操作
12. 三角形の面積
13. 建物の面積
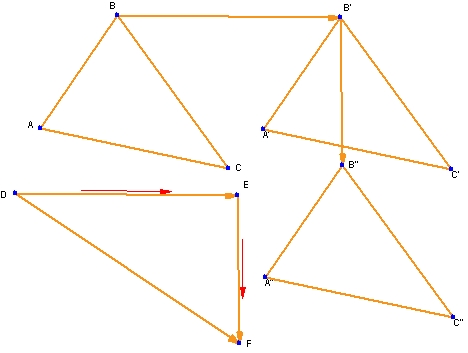
10. スライドベクトル
この例も、シカゴ大学学校数学プロジェクトの『代数学』 (Scott, Foresman) からの引用です。この教科書では、この問題を座標を使って解いています。Geometry Expressions でも座標を使うことはできますが、その必要はありません。以下の図では、三角形 ABC の位置をスライドベクトル BB’ で定義した別の位置にスライドさせ、その後、B” にスライドさせています。この2つのスライドベクトルを追加することで、DF によって定義される単一のスライドの効果を調べることができます。
以下に示す3つの例は、シカゴ大学学校数学プロジェクトの『高等代数学 (Advanced Algebra)』 (Scott, Foresman) からの引用です。
11. 関数の鏡映操作
この図は、直線 y = x を軸とする曲線 y=x2 の鏡映を示すものです。Geometry Expressions では、鏡映、併進、および、伸縮操作を実行することができます。
12. 直角三角形の連続作成
この例は、教科書では、以下の図に示す三角形が最初の2つのみ示され、辺 BC の値には “3” が指定されています。出題されている問いは DC の長さを求めることです。三角形をさらに作成してゆくと状況は複雑になり、特定の数値を使用することでパターンが分からなくなってしまうでしょう。Geometry Expressions では、数式の使用が可能であることに加え、この流れで更に幾つかの三角形をシンプルで迅速に描画することができます。n 番目の斜辺が (n+1)1/2 であることは、これにより容易に理解できます。
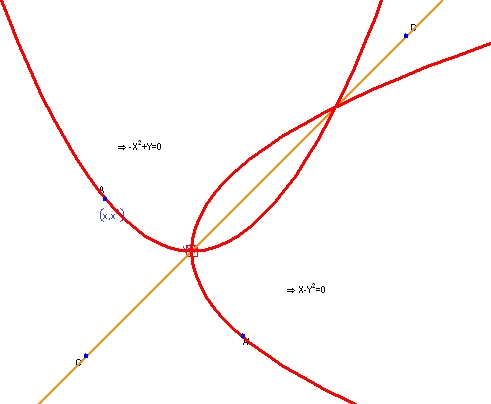
13. 双曲線
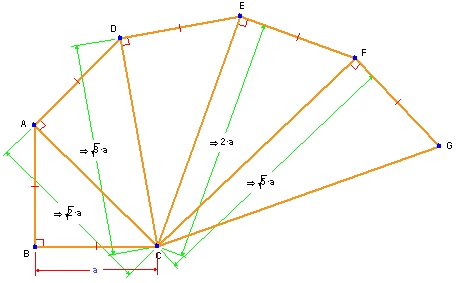
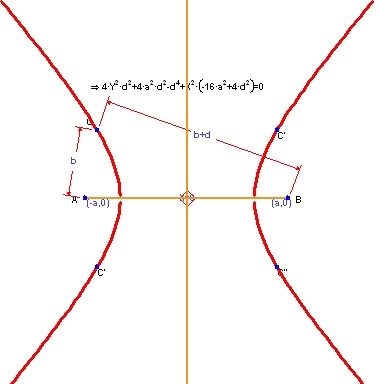
この例は、円錐の断面を元に作成したもので、その中でも、固定された2つの点からの距離の差が一定となるような2つの点の軌跡として定義された双曲線をあらわすものです。以下の図は、固定する2つの点を A および B とし、変動する点を C としたものです。CA と CB の距離の差を一定の値 d とします。Geometry Expressions を使えば (他の動的幾何システムとは異なり)、これらの距離を数式であらわすことができます。システムによってその軌跡 (双曲線) を作成できるだけでなく、その方程式を求めることもできます。
(6)動的作図
14. 周波数、振幅など
15. 区分関数
16. 区分近似
17. 有理4次式
18. 円錐曲線の軌跡
19. 円錐曲線の包絡線
20. 円の極限
14. 周波数、振幅など
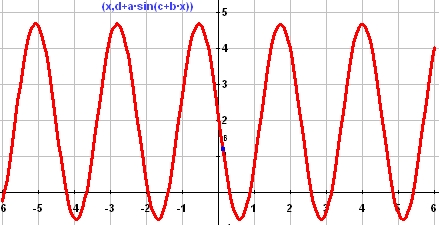
これは、関数 a*sin(b*x+c) + d を示したものです。振幅、周波数、位相シフト、オフセットなど、学生がこのパラメータのいずれかを動的に変更すると、それに応じて変化する内容を即座にグラフ上で確認することができます。
15. 区分関数
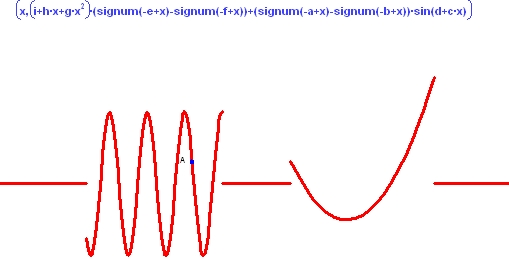
区分関数の研究にこのアプリケーションを利用することもできます。
以下の図で、2つの窓とその2つの関数の係数が数式である点に注目してください。これらはいずれも動的に変更できます。これにより、ユーザーは、ある窓の関数の属性をそれ以外の窓の関数とは区別して変更することができます。
16. 区分近似
この例では、特定の窓における正弦関数に最もあてはまる近似となるように2次式の係数を動的に変更します。この作業が完了したら、学生はその後、窓の幅を広げてゆき、こうした近似が非常に限定された範囲にしかうまく行かないことを、言わば劇的な形で理解します。
17. 有理4次式
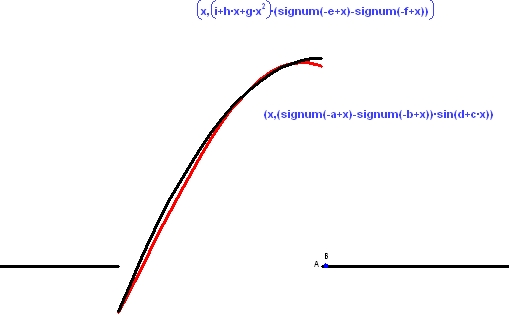
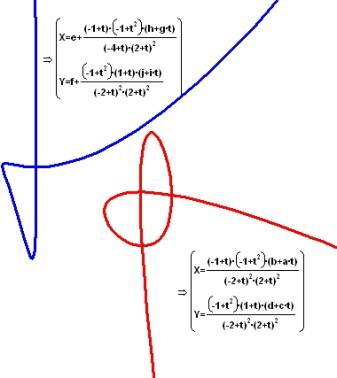
代数曲線を学ぶ上で重要な問題のひとつに、ある曲線が有理式であらわせるか否か、すなわち、有理関数を使ってパラメータ化することのできる曲線の決定があります。この問題で重要な点は、曲線における重複点の概念 (例:ループとカスプ(尖端)の関係) です。代数曲線が有理式であらわせることと、それが有する特異点の数と種類の間には密接な関係があります。しかし、この関係は単純ではありません。例えば、3つの重複点をもつ4次式は必ず有理式になりますが、重複点の数がそれより少ない4次式でも有理式になるものがあります。これは、学生にとって可視化することがきわめて役に立つ絶好の問題です。
上の図で赤の曲線と青の曲線はいずれも有理4次式です。座標がシフトしている点を除けばパラメータ化された式はどちらも同じだからです。2つの曲線の間にある表示上の違い (実平面上で赤の曲線には3つの重複点があるのに対して、青の曲線には重複点が1つしかない) は、係数 a, b, c, d, g, h, i, および j の選択が違うだけです。
18. 円錐曲線の軌跡
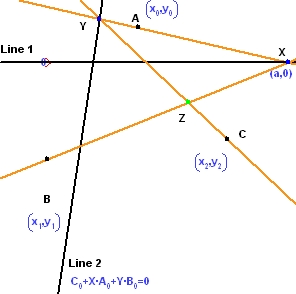
可視化するのは非常に困難ですが、Geometry Expressions を使うことできわめて分かりやすくなる幾何学問題をもうひとつ紹介します。2つの直線上の2つの点を対応させてできる2つの範囲からできる円錐曲線の軌跡です。この状況を示したのが、以下の2つの図です。
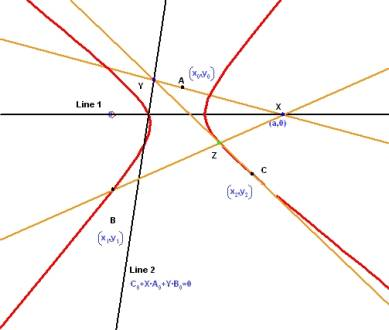
まずはじめに3つの点 A, B, C と、2つの直線 Line1 と Line2 を作成します。作図の手順は以下の通りです:
- 直線 1 の上に任意の点 X を配置します。最初の直線は水平になるよう作成し、配置した点の座標は (a,0) を選択します。こうして与えられたパラメータ a が軌跡の作成に使用されることになります。
- 次に、X と与えられた3つの点の1つ目 A によって定まる直線を定義します。
- この直線と与えられた2つ目の直線 (Line2) により、唯一の点 Y が定まります。
- 変動点 X と与えられた2つ目の点 B により直線 XB が定まります。
- 点 Y と与えられた3つ目の点 C により唯一の直線 YC が定まります。
- 直線 XB と YC により、以下にグリーンで示した唯一の点 Z が定まります。
X を Line 1 に沿って動かすと、それに応じて Z も移動します。はっきりとは分かりませんが、以下に示すように Z によって円錐曲線がトレースされています。
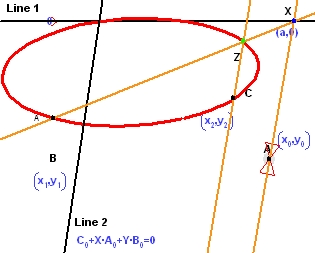
ここでパラメータ a の値を動的に変化させると、点 Z が円錐曲線をトレースするのを確認できます。さらに、この特定の円錐曲線は、最初の3つの点と2つの直線の位置によって定められます。Geometry Expressions では、ユーザー自身がこれらの点や直線を動かすことで、円錐曲線の軌跡全体を動的に変化させることができます。以下の図は、点 A を別の位置にドラッグしたもので、A の移動に応じて円錐曲線が双曲線から楕円に変化しています。
19. 円錐曲線の包絡線
![]() サンプルデータ:
サンプルデータ:
前の例は、2つの直線上の2点を対応させてできる2つの範囲の射影的属性に依存するものです。対応する二重作図の属性が投射的であるということは、2点を通る2つの対応する直線束についての結果も二重になることになります。こうして作成された後者の円錐曲線は、1点でトレースされた円錐曲線の軌跡ではなく、円錐曲線の接線の包絡線になります。
以下の図はこうした状態を示すもので、前の例で紹介した二重作図を以下に示します。
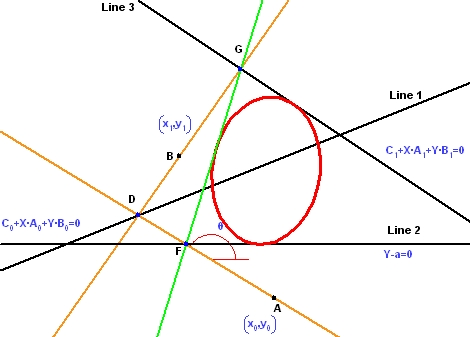
3つの直線 (黒で表示) と2つの点 A と B があるとします。
- 最初の点 (A) を通る任意の直線を作成します (直線 AD と水平線のなす角を θ とします。このθ が包絡線を作成するパラメータとなります)。
- 作成した直線と最初に与えられた直線から点 D が定まります。
- 点 D と与えられた2つ目の点 (B) により直線 DB が定まります。
- 変動直線 AD と与えられた2つ目の直線により点 F が定まります。
- 直線 DB と与えられた3つ目の直線により点 G が定まります。
- 点 F と G により直線 FG (グリーンで表示) が定まります。
θ が変化すると、この直線も動きます。これらの直線の包絡線は以下の赤で示す円錐曲線となります。この円錐曲線は、前の例で最初の3つの点と2つの直線で定められたものと同様、最初の3つの直線と2つの点によって定まります。これらの直線と点が変わると、円錐曲線の包絡線全体も変わります。
20. 円の極限
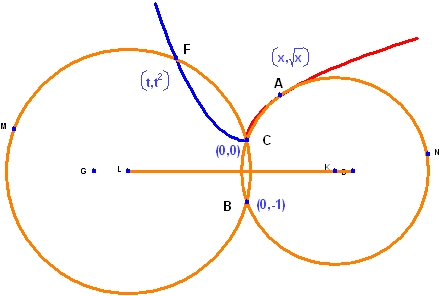
円のひとつを A, B, C で定義し、もうひとつの円を B, C, F で定義します。A を曲線 y=√x 上の点とし、F を曲線 y = x2 上の点とします。点 F と A をそれぞれ独立して変化させることができるように、ここでは、2つ目の曲線のパラメータに t を使用しています [Geometry Expressions では、直交座標系の変数に大文字の X と Y が使用されます。ここでは、小文字の x を A を通過する曲線のパラメータとして使用しています]。
ここで、x と t がゼロに近づくにつれて、A と F は C に重なる点に注意してください。ゼロの位置までくると、2つの円の定義が消滅します。どちらの円も区別できない3点では定義していませんが、果たして、この極限における2つの円は、本当に矛盾なく定義されているのでしょうか?
パラメータ x をゼロに近づけてゆくと、それに対応する円が大きくなってゆくあることが分かります。
t をゼロに近づけてゆくと、点 B, C, F によって定義される円はそれに応じて小さくなります。
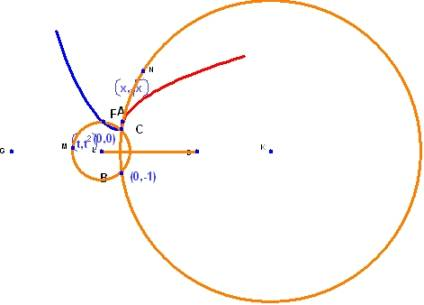
ここで何が起こっているのかを良く理解するために、Geometry Expressions で2つの円の方程式を求めてみましょう。
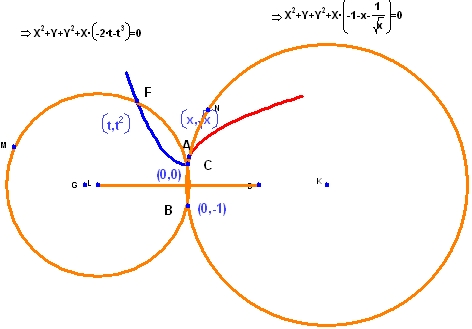
ここで、t をゼロに近づければ、F を通過する円が中心を (0,1/2) とする円に近づくことが分かります。一方、x をゼロに近づける場合は、A を通過する円が Y 軸に近づくのが分かります。