折り重ねを用いる一部実施要因計画
1.はじめに
実験プログラムの初期の段階で、その全体像を一度に描き出そうとするあまり、既知の因子をすべて盛り込んだひとつの包括的な実験を、計画したくなる誘惑に駆られる人がいるかもしれません。
しかし、これを計画するには重要な因子が何であり、その最適水準が何であるかを完全に特定し得ることが前提となります。これよりも危険性がずっと低く効率的な代わりになるアプローチがあります。
それは、規模の小さな実験を逐次的に構成していく方法です。小規模な実験を複数行い、その都度結果を評価することを通じて、次にどのような実験を計画すべきかが、自ずと明らかになってきます。途中で除外される因子もあるでしょう。逆に追加される因子もあるでしょう。そして、求める水準は少しずつ最適な範囲に近づきます。
逐次的な実験の構成要素を用意するには、実験を細かく分割するのがよい選択です。
実験の分割には、Plackett‐Burman 計画法を使用する方も多いですが、このチュートリアルでは標準的な2水準アプローチ、すなわち、Design‐Expert® に用意された “Min Run”(最小試行)オプションを使用します。いずれのアプローチを採用するにせよ、分解能の低いこのような計画から導き出される効果をどのように解釈していいか分からず困惑する人がいるかもしれません。
特に問題となるのは、主効果がもっともらしい2因子の交互作用でエイリアス(別名)化される場合です。もしそのような問題が起こる場合、折り重ねを計画し、実験を追加試行することによって、交絡の削除を期待できます。この技法は、元の計画行列に新たな部分行列を付け足すものです。
これから議論する折り重ね計画でできるのは次のことです
- 主効果から2因子交互作用による影響を排除する
- 主効果とその2因子交互作用を、他の主効果と2因子交互作用から非エイリアス化する
Design‐Expert の “Foldover” 機能は、どちらの折り重ねタイプでも、必要な計画ポイントを自動的に追加します。
2.飽和計画の例
ランス・レッグストロングは、早春自転車競技大会に備えて自転車の最終調整を行います。大会が開催されるまでに残された期間は1週間です。
彼は4分の1マイルのトラックを 8周だけ走行して、7つの因子を検定することにしました。以下に示すのはランスが作成した計画表で、Design‐Expert のデフォルトの factorial タブに用意された “2‐Level Factorial” 計画ビルダーでセットアップ可能です。
この計画は、因子が “saturated”、すなわち、与えられた数の試行に対してこれ以上因子を追加できない状態にあります(この事例の着想は、Statistics for Experimenters, 2nd Edition(Wiley, 2005)by Box, Hunter and Hunter(“BHH”)から来ています。BHH は第6.5章で、取り扱う因子が少ないため結果は以下に示すものとは異なりますが、これと非常に似た研究を報告しています)。
| 「テレビの調子が悪くてうまく映らない場合、ある場所をキックすれば、少なくとも当分の間は問題が解消することがよくあると思います。しかし、長期的解決策を講じるには、この不具合の起こる真の理由を突き止める必要があります。一般に、問題は一時的に解消されるか、抜本的に解決されるかのいずれかです。解消と解決の両方を仲立ちするのが実験計画法 DOE です。」 ‐‐ Box, Hunter and Hunter. |
| Std | Run | A: Seat | B: Tires psi | C: Handle Bars | D: Helmet Brand | E: Gear | F: Wheel covers | G: Generator | Time 1/4 mile secs |
|---|---|---|---|---|---|---|---|---|---|
| 1 | 2 | Up | 40 | Up | Windy | Low | Off | Off | 77 |
| 2 | 1 | Down | 40 | Up | Atlas | High | Off | On | 74 |
| 3 | 4 | Up | 50 | Up | Atlas | Low | On | On | 82 |
| 4 | 7 | Down | 50 | Up | Windy | High | On | Off | 47 |
| 5 | 6 | Up | 40 | Down | Windy | High | On | On | 72 |
| 6 | 3 | Down | 40 | Down | Atlas | Low | On | Off | 77 |
| 7 | 8 | Up | 50 | Down | Atlas | High | Off | Off | 48 |
| 8 | 5 | Down | 50 | Down | Windy | Low | Off | On | 83 |
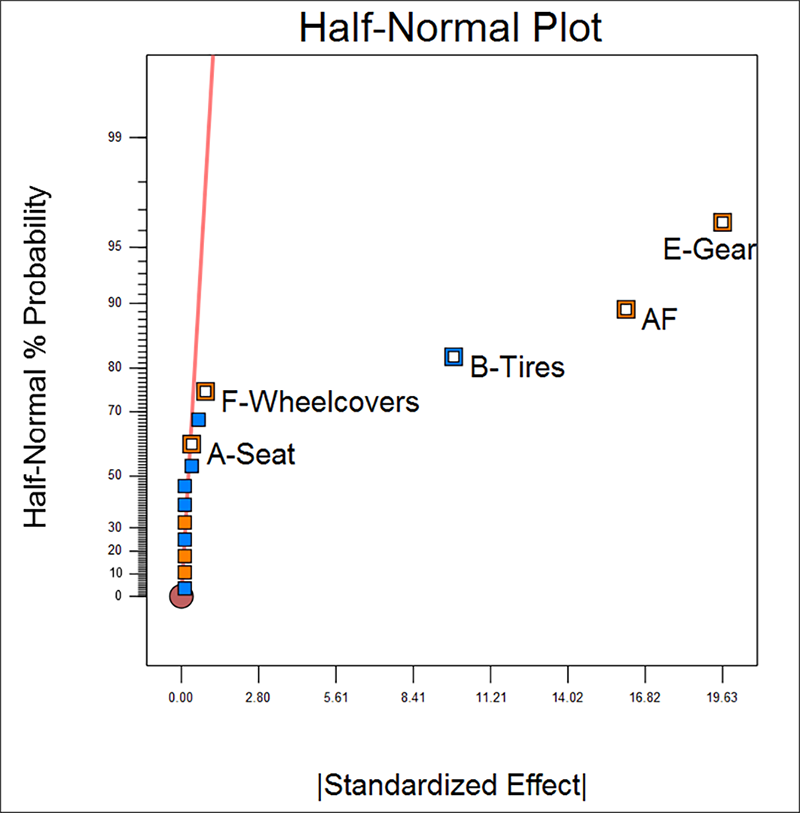
以下の評価結果を見てすぐにお分かりいただけるように、これは主効果のすべてが2因子交互作用と交絡する分解能 III 計画のひとつです(分解能が低い計画であるという注意をユーザーに喚起するため、Design‐Expert の計画ビルダーでこれらは赤のフラグで表示されます)。
ランスは分解能 V またはそれ以上の実験を実行したいと考えます。これなら、主効果とその交互作用を明確に評価できるからです。残念なことに、Stat‐Ease 社の統計学者によって考案された “min‐run Res V” 計画(別名 “MR5”)を使えば、試行回数が最低でも30回は必要となります。しかし、大会までに残された期間はわずかしかありません。試行数 30 回は多すぎます。ランスはしばらく考えて、中間の分解能 IV 計画(現在、Design‐ Expert に黄色で警告されている計画)を選択しようとしますが、それでも16回の試行が必要なので、8回の試行だけで実行できる分解能の低い分解能 III を実行することに決めました。

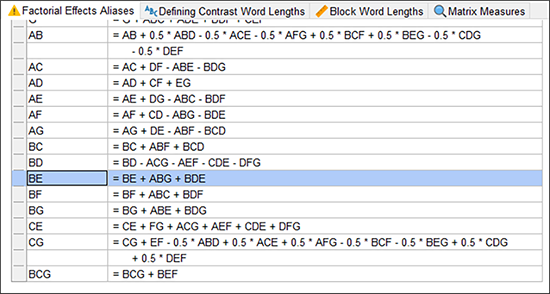
データ入力の時間を節約しましょう。“Help” -> “Tutorial Data” -> “Biker” をクリックして、実験結果を読み込みます。データを一通り眺めたら、左側にある “Evaluation” ノードをクリックして、計画のエイリアス構造を点検してください。試行数の少ないこの計画では、 Design‐Expert は主効果の順序に対する応答しかモデル化できないと判断している点に注意してください。プログラムは 3FI 以上の項は無視する設定がなされているので、2因子交互作用(2FI)までのエイリアス化を表す結果が生成されることになります。
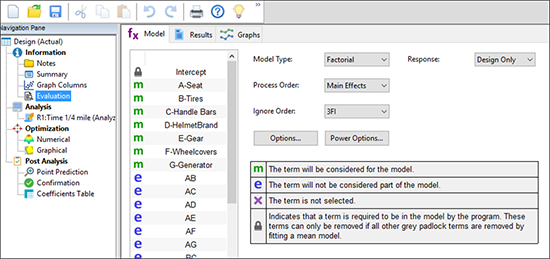
それでは、データウィンドウの上部にある “Results” ボタンを押してから、“Aliases”タブを選択して、この事例における分解能 III 計画の試行のみに関する影響が表示されます。
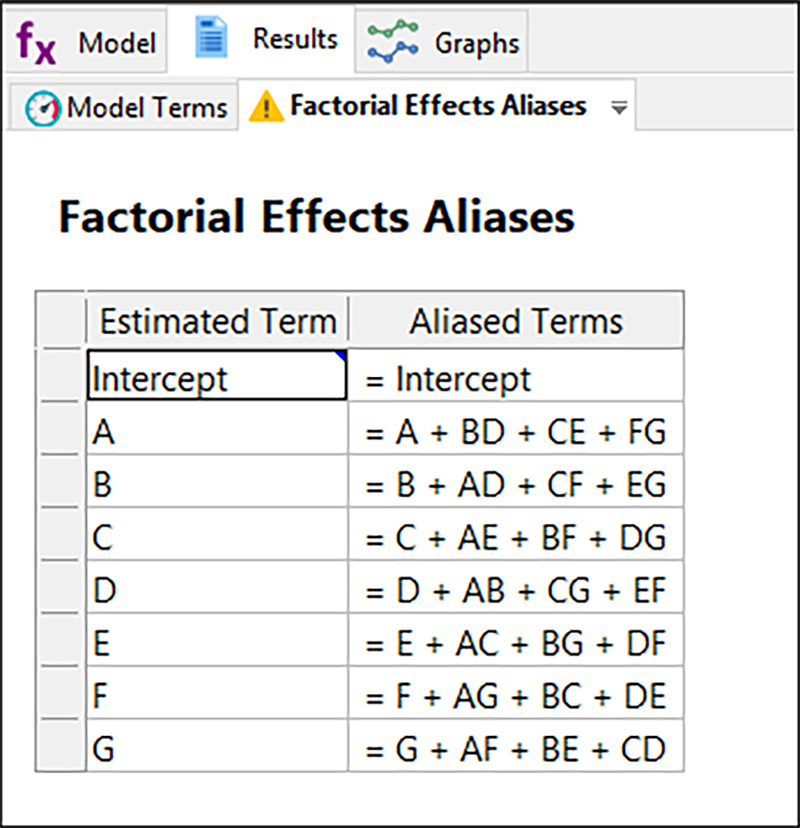
表示された計画は全体の 1/16 番目です。従って、以降の効果もそれぞれ他の 15 の効果でエイリアス化されることになりますが、その殆どは画面を不必要に占有してしまうため、デフォルトでは無視するよう設定されています。この出力結果は、いずれの主効果も3つの2因子交互作用と交絡することを表しています。
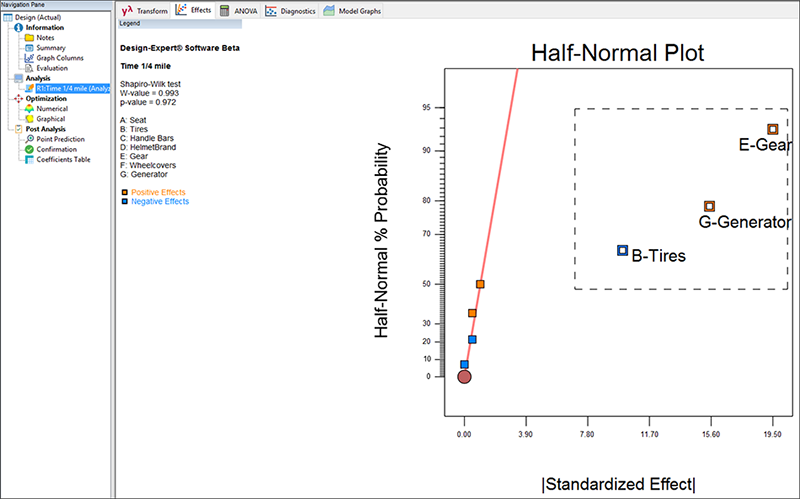
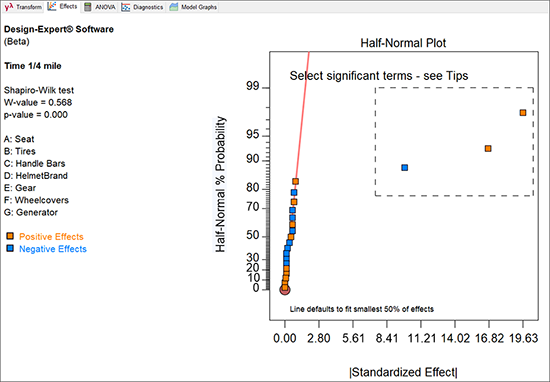
評価レポートの残りの内容については、ここでは触れません。左側の Analysis ブランチにある “Time 1/4 mile” ノードをクリックして、画面ウィンドウ上部の “Effects” をクリックしてください。最大効果を右から順番に3つクリックしてください(以下の図のようにマウスで範囲を選択しても同じです)。
次のパレート図において、表示されたチャート上の最大のバー(E)を右クリックすれば、以下のようにそのエイリアスが表示されます。
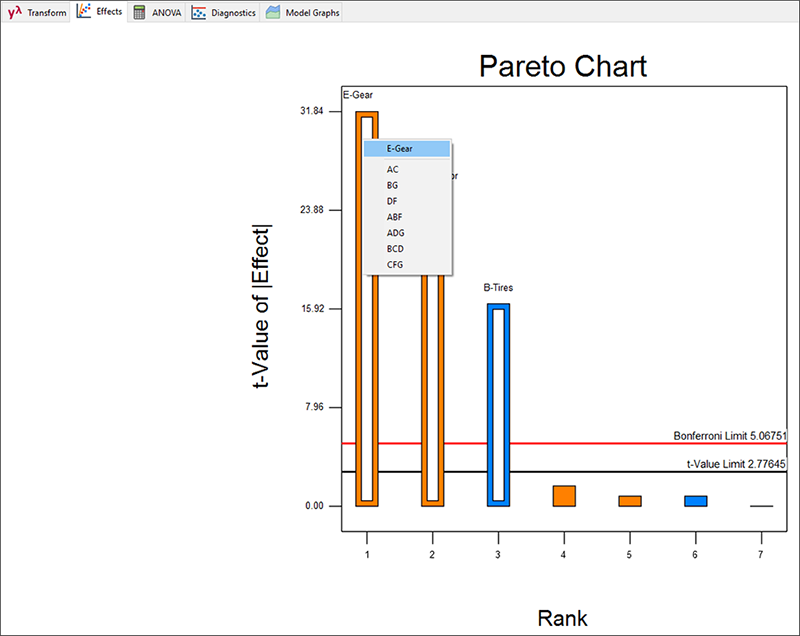
因子 B(タイヤ)、E(ギア)、G(発電機)は、明らかに有意です。“ANOVA” をクリックして、これを統計的に検定してみましょう。ANOVA 画面が現れる前に、この計画がエイリアス化されていることを思い起こさせる以下の警告ダイアログが表示されます。
この内容は既に計画の評価段階で承知していますので、“No” をクリックして続行してください(オプション:Yes をクリックした場合は、前の画面に戻ってリストが表示されます。内容を確認したら ANOVA ボタンをクリックしてください)。
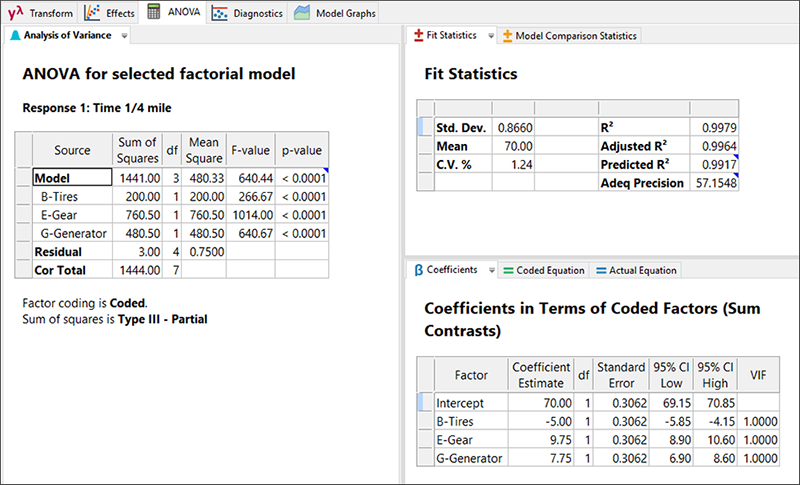
ランスは、実験データをうまく当てはめることができました。因子 B の係数が負の値であることから、タイヤの固さが固いほどトラックの走行にかかる時間は落ちるようです。また他方で、因子 E と G の係数が正の値を示していることから、ギアを高くし、発電機をオフにしておいた方が、速度が出ることがわかります。一見したところ、このアプローチは全体として非常に科学的で決定的であるかのように見えます。実際、ランスはこの実験結果に基づいて自転車を最終調整した結果、レースに出場して優勝したのですから!
しかし、ランスの友人(であり個人的なコーチでもある)シェリル・ソングバードは、この結論が誤りであることに気が付きます。彼女が指摘するのは、この計画の主効果はいずれも2因子交互作用と交絡している点です。真に有意な要因は、交絡する交互作用のどれか一つである可能性もあるわけです。「この件をクリアするまでは、少なくとも、もう1回実験する必要があるね」とシェリルは言います。ランスは「それはいい考えだ」とうんざりしながら答えました。自転車の理想的なセッティングに関する疑念が残ったままであることが分かり、これでおちおち休むことはできないと気付いたからです。
3.完全な折り重ね計画
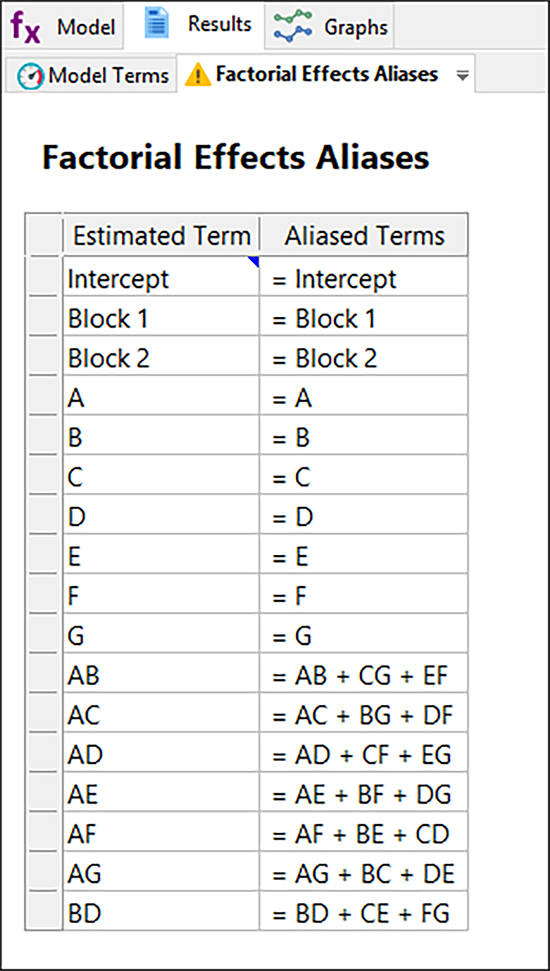
ランスが最初に行った分解能 III 計画の交互作用で生じた主効果の「もつれ」を解くにあたり、試行の “foldover” を利用することができます。これはオリジナルの8回の実験で得られた信号を、丸ごと反転させるものです。反転によって得られた試行ブロックをオリジナルの試行ブロックと一緒にすることで、分解能 IV 計画が出来上がります。これにより、すべての主効果は、2因子交互作用(2FI’s)の絡みから開放され自由な状態となります。ただし、2因子交互作用(2FI’s)についてはいずれも、依然として互いに交絡したままです。
それでは、折り重ね計画の新規試行を作成してみましょう。“Design” ノードをクリックし、メニューから “Design Tools” -> “Augment Design” -> “Augment” を選択してください。
これを選択すると、以下のダイアログが表示されます。
Design‐Expert のデフォルトで提示される増補オプション Foldover はこれで良いので、“OK” をクリックして進んでください。次に、どの因子を折り重ねに採用するかのリストがプログラムに表示されます。Design‐Expert デフォルトは、すべての因子が選択されるよう設定されています。これは完全な折り重ねを表します。因子の選択は、因子を右クリックするか、因子をダブルクリックすることで指定または解除することができます。
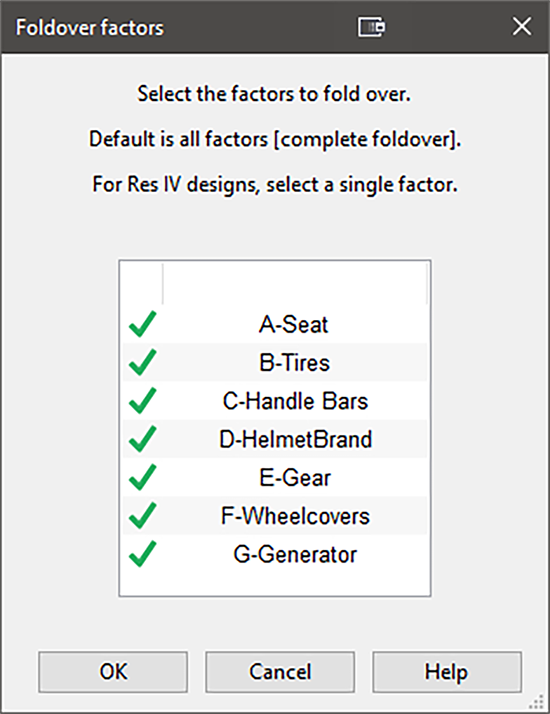
この事例では、すべての因子を折り重ねにするのが最良の選択ですので、“OK” をクリックして次に進んでください。以下の警告がプログラムに表示されます(どちらかと言えば提案ですが)。
“Yes” をクリックすると別の警告が表示されます。
“Yes” をクリックしてください。この警告では評価のためには欠損データを伴う応答を選択することがリマインドされます。データを伴う行のみが評価されます。すべてのデータを評価するには、Response を “Desing Only” にしたままで “Results” を押すと増補された計画の評価結果が示されます- 結果は良好です!
分解能 III 計画の完全な折り重ねで、分解能 IV 計画になりました。その証拠に、主効果が今度は3因子交互作用のみでエイリアス化されています。ただし、3因子交互作用は殆ど起こりそうにないため、デフォルトでは無視するよう設定されています。このようなことがなぜ起こるのかは、Montgomery 著のテキスト『Design and Analysis of Experiments』を参照してください。ところで、実験の試行回数を2倍にすると検出力も増加します。このことを評価したい場合は、Results を再計算する前に Model 画面に戻り、Order を Main effects に変更してください。変更したら “Terms (Power)” ボタンを押してください。
それでは、メインの Design ノードに戻って、メニューから “View” -> “Display Columns” -> “Sort” -> “Std Order” -> “Ascending” を選択してください(Tip: 任意の列をソートするには、そのヘッダーを右クリックすると簡単に実行できます)。ブロック2の各試行が、ブロック1と試行と比べてどのように反転しているかをよくご覧ください。例えば、ブロック1の Seat(因子1)は Up, Down, … と続いたのに対して、ブロック2では、down, up, … と続いています。すべてが逆に並んでいます。
ランスの行った追加試行の結果は、以下の表のようになりました。
| Std | Blk | A: Seat | B: Tires psi | C: Handle Bars | D: Helmet Brand | E: Gear | F: Wheel covers | G: Gener-ator | Time 1/4 mile secs |
|---|---|---|---|---|---|---|---|---|---|
| 9 | 2 | Down | 50 | Down | Atlas | High | On | On | 57 |
| 10 | 2 | Up | 50 | Down | Windy | Low | On | Off | 93 |
| 11 | 2 | Down | 40 | Down | Windy | High | Off | Off | 84 |
| 12 | 2 | Up | 40 | Down | Atlas | Low | Off | On | 87 |
| 13 | 2 | Down | 50 | Up | Atlas | Low | Off | Off | 94 |
| 14 | 2 | Up | 50 | Up | Windy | High | Off | On | 57 |
| 15 | 2 | Down | 40 | Up | Windy | Low | On | On | 86 |
| 16 | 2 | Up | 40 | Up | Atlas | High | On | Off | 83 |
ランスと一緒に以下を続けることにしましょう。Response 1 列の折り重ねブロック(Block 2)にある8回の試行に、彼の記録した上記のタイムを以下のように入力してください。まず始めに、計画の行列を標準順序(Std Order)でソートしているか、必ず確認してください。入力する因子と応答は必ず一致させる必要があります。そうしなければ、この分析は無意味になります。

“Time 1/4 mile” ノードをクリックして、“Effects” プロットを表示してください。最大効果を右から順番に3つクリックしてください(以下の図のようにマウスで範囲を選択しても同じです)。
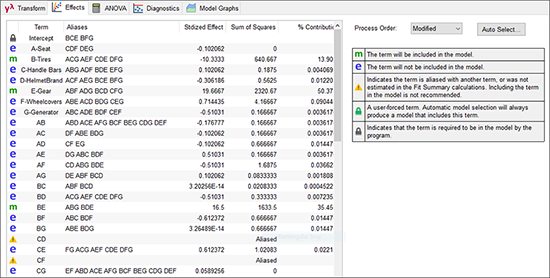
効果 G であると見なしていたものが、今回は AF としてプロットに表示されています。しかし、注意してこの計画の評価を思い出してください。この折り重ね計画においては、AF は BE と CD と共にエイリアス化されています(このことを確認するには、前に戻ってスクリーンショットを見直すか、画面上の Evaluation を押して Report をご覧ください。あるいは、こちらの方がよりお勧めの方法ですが、半正規プロット上にある AF を上図に示すように右クリックしてみてください)。Design‐Expert では、AF のみが選択されていますが、これは、すべてのエイリアス項のうちアルファベット順でもっとも上にくるものだけが表示されるようになっているからです。
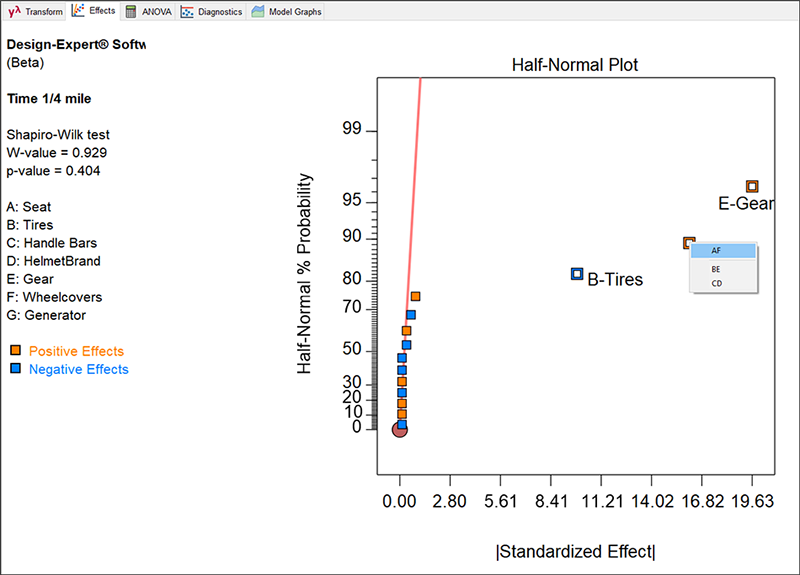
ランスとシェリルは、自分たちの主題に関する経験的知識から、シート位置とホイールカバーとの交互作用 AF は現実には起こり得ないことを知っています。また、ハンドルバーの位置とヘルメットメーカーとの交互作用 CD も存在しないはずです。彼らは、タイヤの空気圧とギアとの交互作用 BE のみが現実的に起こり得る交互作用であることを確信します。とはいうものの、デフォルトで AF の2因子交互作用を持つこのモデルの ANOVA を調べてみることにしましょう。
ソフトウェアは、モデルの階層構造に関する以下の警告を表示します。
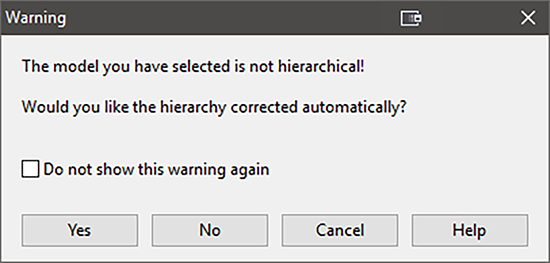
交互作用 AF を選択したため、その親因子である A と F を必ずモデルに含めて階層構造を成立させる必要があります。これによって、モデルは数学的に完全な状態になります。“Yes” をクリックして、モデルの階層構造を是正してください。
新たに追加した2つのモデル項 A と F は、効果がゼロに近い重要でない多数の集団に属することに注目してください。ここから、2つのいずれかまたは両方とも統計的にあまり有意ではないと思う人がいるかもしれません。しかし、この2つの項を含めることがここでは重要なのです。
もう一度 “ANOVA” ボタンをクリックして先に進めます。今度は、“This design contains aliased terms. Do you want to switch to the View, Alias list…?”(この計画にはエイリアス項が含まれています。Alias list に表示を切り替えますか?)と警告が表示されます。“No” をクリックして次に進めてください(この Alias List には、後から戻ることができますので、ここでは心配しないでください)。
ANOVA の結果は良好です(因子 A は有意ではありませんが、モデル内の階層構造を裏で支えます)。
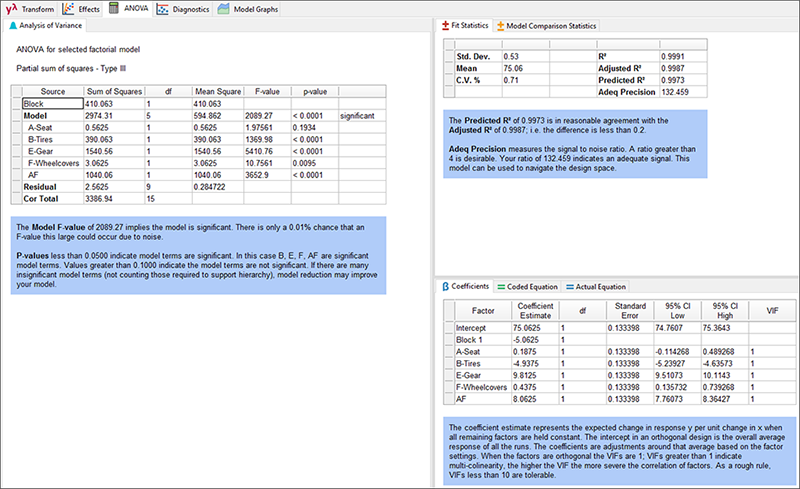
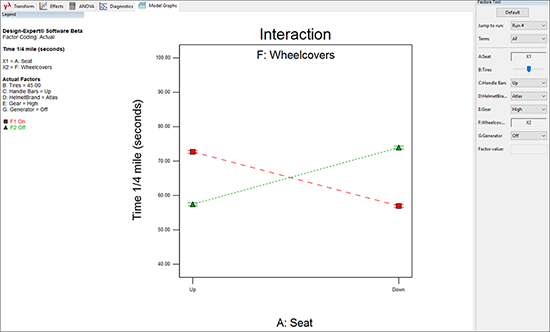
“Diagnostics” をクリックしてください。問題は特に見つからないはずです。次に、“Model Graphs” をクリックして、交互作用 AF のプロットを表示させてください。A も F も主効果としては応答に目立った変化をもたらさないため、交互作用のグラフは以下のようにクロスします。
ランスとシェリルは、シート位置とホイールカバーによるこの交互作用が実際には起こり得ないことを経験から知っています。従って、グラフに表示されている内容は、必ずしも適切なものではないことに留意してください。
4.エイリアス化された交互作用の調査
ランスは、AF と共にエイリアス化されたその他の、より妥当性のある、交互作用を調査することにしました。実際にコンピュータを操作しながら、ランスと同じ作業を確認していきましょう。ランスは、“Effects” タブをクリックして前に戻り、 “Numeric” タブを選択して、このウインドウを最大化します。
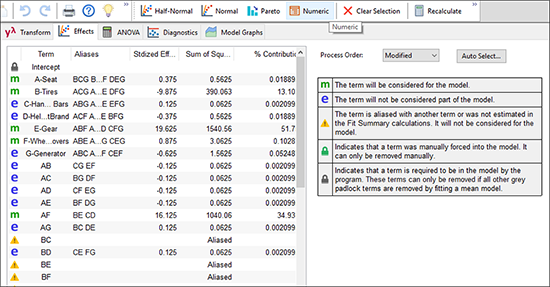
彼は、項 AF にマウスを移動し、左下にあるように、右クリックした後、BE を選択しました。結果は次のスクリーンショットのようになります。
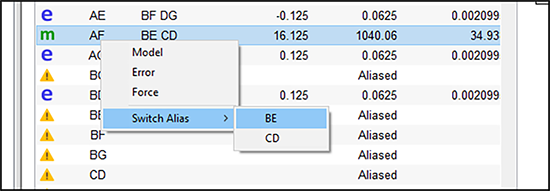
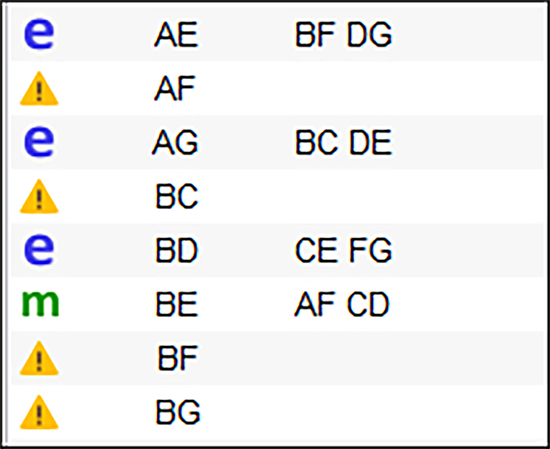
この操作は、リバーシブル(反転可能)であることに注意してください。すなわち、BE から AF に戻すことも同じ操作で変更できるということです。しかしここでは、本題に戻って、ランスは “Pareto” タブを選択します。効果 A と F は、交互作用 AF の階層構造の成立を支えるという点において前のモデルと同じです。
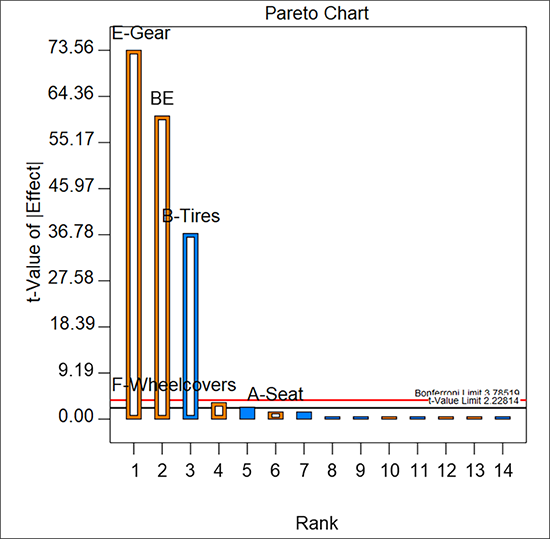
現在、交互作用 AF は BE に置き換わっています。2つの主効果 A, F が有意でないことはグラフから明らかですので、“F”(ランク4位)と “A”(6位)のラベルの付いたバーをクリックして、痕跡物としての価値しかないこれら二つのモデル項を無効にしてください。効果 B、E、BE をひとつのファミリーとして簡素化するこのやり方に注目してください。つまり、このモデルは各々が独立して有意となるすべての項で、階層構造を成立させたと言えます。原則として、簡素化モデル(統計学的に言えば「parsimonious:節約」)は、それよりも多数の項を必要とするものに支えられるべきものです。特にこのことは、前に作成した親因子のない AF を使った例のように、それ自身では有意でない親の項をもつモデルに関しても当てはまります。
次に、ランスは交互作用 BE を表示します。“Model Graphs” ボタンをクリックして、これをご確認ください(エイリアスの交互作用を表示するアドバイスが表示されたら “No” をクリックしてください)。
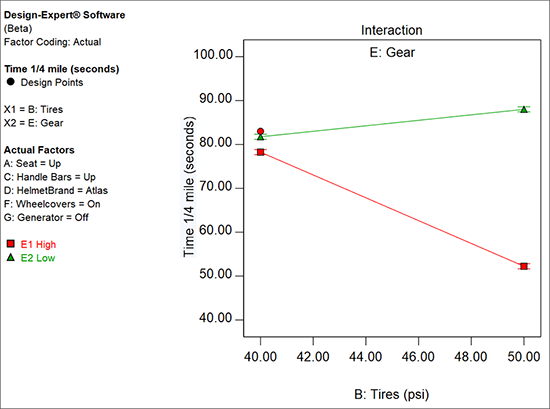
ランスはこちらの方が遥かに納得のいくものであると考えます。
Design‐Expert のグラフ上に赤いポイントが表示される点に注意してください。これは、実測値のひとつで、ある条件が揃わない限り表示されないものです。ポイントをクリックして、この条件の内容を確認してみましょう。
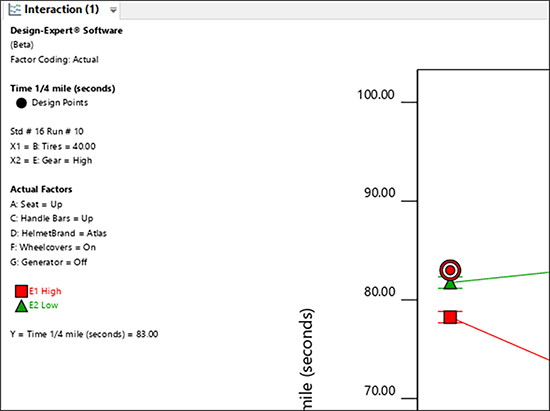
グラフの左側にその内容を確認できます。
このポイントにおけるタイヤ圧(B: Tires)は 40 psi 、ギア(E: gear)設定は High となっています。その上には、試行番号(Run #:無作為化により実際の番号とは異なります)と、計測タイム 83 秒を確認できます。
このグラフには表示されていませんが、因子は一般にデフォルトで指定された平均水準をとります。
本件の場合は因子がカテゴリ型であるため、その因子の低水準がソフトウェアの判断によって(赤のスライドバーが左側に)選択されています。
この内容は、標準の順番(Std Order)でソートした折り重ねの最終行と一致します(注記:実際の試行番号 Run # は、無作為化によりグラフの左側に表示された内容とは異なる場合があります)。
結果を高低両水準の平均値として表示させたい場合は、Factors Tool のリスト矢印をクリックして、以下のように “Average” を選択してください(因子 A:Seat、C:Handle Bars、D:Helmet Brand、F:Wheelcovers、G:Generator については既に設定済みです)。
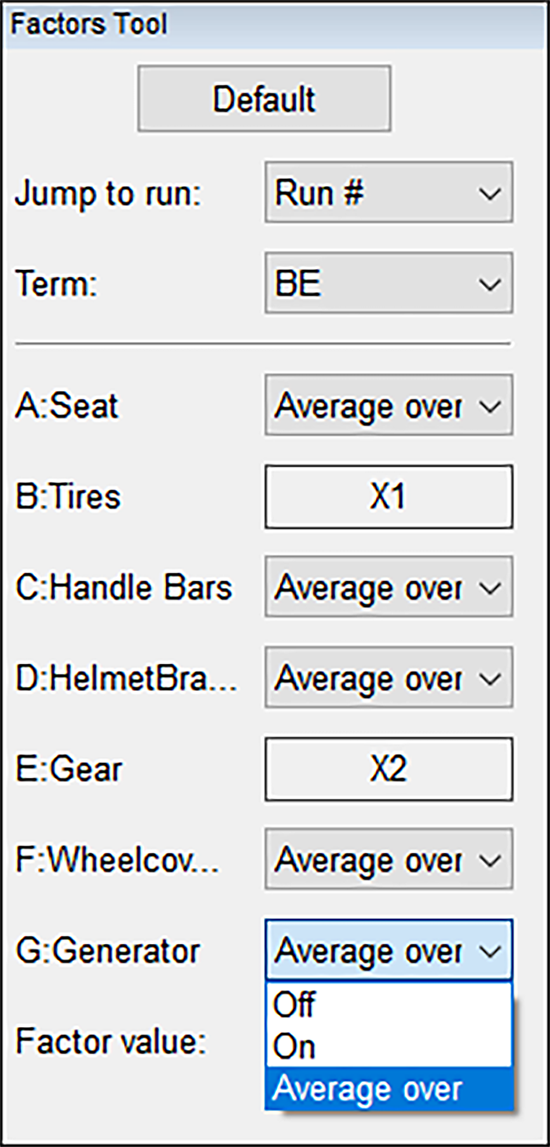
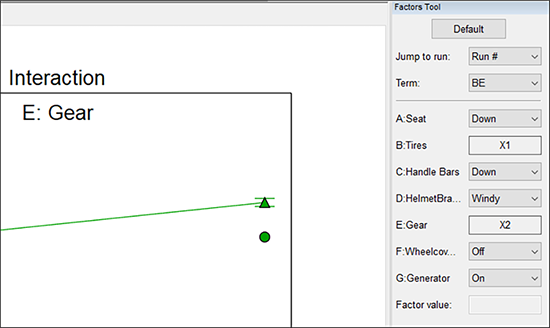
平均値としてのシートの高さは実際に測定された水準ではないので、グラフに表示されていたポイントは非表示になる点に注目してください。交互作用プロットをオリジナルの設定に戻すには、Factors Tool にある “Default” をクリックしてください。元の設定に戻ったら、他の設定も試してみましょう。実際に実験が行われた条件が他にも見つかるでしょうか。なお、理論的に可能な 128(27)通りの組み合わせのうち、折り重ねを使って増えた試行は全部で16回に過ぎないことを思い出してください。従って、もしそれらがグラフ上にあったとしても、それほど多くはなないはずです。例えば、Factors Tool で因子を以下のように(Generator を高水準に)設定すると、別の実測ポイント(緑の円)のひとつが見つかります。
ランスは、すべての成分を一通り見渡すために、C(ハンドルバー)と D(ヘルメットメーカー)が互いに作用しあうとは思えないのですが、交互作用 AF の二番目のエイリアス:CD の効果も調べることにしました。交互作用プロットで得られた結果は全く違ったものでした。意外な結果です!もしお時間があれば、実際に確認してみてください。“Effects” ボタンに戻って、“Alias List” を選択したら、右クリックメニューを使って BE を CD に置き換えます(階層構造にするため、後から因子 C と D をモデルに組み入れる必要があります)。自転車乗りとしての経験的知識が、ランスに思い切った判断を下させました。彼は BE こそが真の効果であり、CD ではないことを頭から決めてかかったのです。
さて、作業内容を保存する良い機会になりました。メニューから “File” -> “Save As” を選択して、例えば「Biker2」などと別名を入力して、ファイルを保存してください。
ランスは、これまでに得られた驚きの結果に触発されて、自転車メーカーにレーサー用の初期設定をどのように変更したらいいかを提言する手紙を書く準備を意気揚々と始めます。しかし、ランスの友人で個人的コーチでもあるシェリルは、2因子交互作用のエイリアス化により、タイヤ圧とギア設定による影響の合成については、依然として立証したことにはならないことを指摘し、「交互作用 BE の効果を確かめるには、三回目の実験を行う必要があるね」と訓戒を込めて忠告します。ランスは「そうするしかないでしょうね」と腹を括ります。
5.1因子の半折り重ね
「実験をあと8回行えば、仮説を証明できるぞ」とシェリルは宣言します。ランスはため息がちに「やりましょう」と答え、「では具体的にどうやったらいいの?」と返します。
「それはね」とシェリルは答えます。「最初にやった2つの実験ブロックと同じポイントを、因子 B についてのみパターンを反転させて試行しましょう。これで、因子 B とその2因子交互作用は、その他の2因子交互作用の影響を受けずに自由になります」。
ランスはこれに反論し、「しかし、そうなると実験をあと16回行うことになりませんか」と食い下がります。「ちょっとまって」とシェリルは続けます「以前、Stat‐Ease 社の記事で『How To Save Runs, Yet Reveal Breakthrough Interactions, By Doing Only A Semifoldover On Medium‐Resolution Screening Designs (試行回数を減らしながら、交互作用の問題を打開するには、半折り重ねを中分解能のスクリーニング計画で実行するしかない)』というのを読んだことがあります(参照:semifold.pdf )。
そこには、折り重ねの半分を実行するだけで、2FI を非エイリアス化するという目的を達成できる方法が詳しく書かれていました。結局ランスはトラックをあと8周走るよう言いくるめられたのでした。
試行をさらに追加作成するには、Design‐Expert の “Design” ノードに戻り、メニューから “Design Tools” -> “Augment Design” -> “Augment” を選択します。今度は “Semifold” を実行するようプログラムに忠告が表示されます。
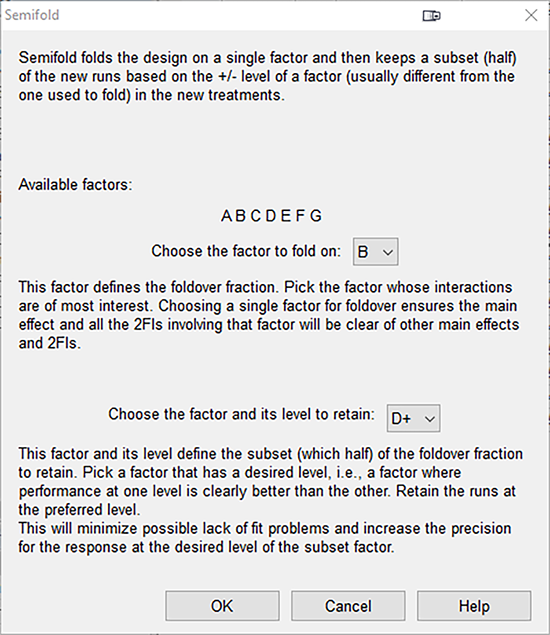
“OK” を押すと、これからランスが走ることになる第3ブロックの試行として、どの試行を追加するかを定義するダイアログボックスが表示されます。Choose the factor to fold on フィールドに “B” を指定してください。ランスとシェリルは、次の質問「Choose the factor and its level to retain」に少し頭を悩ませますが、直ちに “D+” 、すなわち、ヘルメットメーカー Windy を選択します。この因子は間違いなく応答に影響を及ぼさないと判断したからです(また、シェリルはこのブランドのヘルメットをランスがかぶっているのを見るのが好きなのです!)。
ダイアログの “OK” をクリックして、計画評価への移行を了解する “Yes” をクリックしてください。欠損データに関する警告が表示されたら、もう一回 “Yes” をクリックします。現在、Evaluation の開始画面が表示されているはずです。“Results” をクリックして、新たに追加されたエイリアス構造を確認してください。画面を下にスクロールさせて、2FI を表示し、BE が今度は3因子交互作用のみでエイリアス化されていることに注意を払ってください。
例えば AB のように、他の効果が小数点になってエイリアス化されている効果があることに注目してください。これは計画全体を非直交にするために起こる半折り重ねの副産物で、効果をこれ以上独立して評価することはできないことを表しています。後で、このデータを Design‐Expert で分析する際、このことを警告するダイアログが表示されることになります。
メインの “Design” をクリックして、増補された試行を確認してください。Std 列のヘッダーをダブルクリックして、その並びを標準の順序に戻します。
ランスが第3ブロックの実験で試行した結果は以下の表で確認できます。
| Std | Blk | A: Seat | B: Tires psi | C: Handle Bars | D: Helmet Brand | E: Gear | F: Wheel covers | G: Gener-ator | Time 1/4 mile secs |
|---|---|---|---|---|---|---|---|---|---|
| 17 | 3 | Up | 50 | Up | Windy | Low | Off | Off | 98 |
| 18 | 3 | Down | 40 | Up | Windy | High | On | Off | 88 |
| 19 | 3 | Up | 50 | Down | Windy | High | On | On | 61 |
| 20 | 3 | Down | 40 | Down | Windy | Low | Off | On | 92 |
| 21 | 3 | Up | 40 | Down | Windy | Low | On | Off | 91 |
| 22 | 3 | Down | 50 | Down | Windy | High | Off | Off | 60 |
| 23 | 3 | Up | 40 | Up | Windy | High | Off | On | 90 |
| 24 | 3 | Down | 50 | Up | Windy | Low | On | On | 97 |
空の応答フィールドに上記と同じタイムを入力してください。入力したら、すべて正しく入力されているか、再度内容を確認してください。確認が済んだら、Analysis の “Time 1/4 Mile” ノードに移動して、“Effects” ボタンをクリックしてください。この計画が直交(orthogonal)でないことを警告する以下のダイアログが表示されます(前に少し説明したものです)。
“OK” を押したら、最大効果を右から順番に3つクリックしてください(以下の図のようにマウスで範囲を選択しても同じです)。有意となるのは B、E、および、交互作用 BE であることが分かるはずです。
再計算による効果の変化は非常にわずかに過ぎないので、その変化を見落としてしまうかも知れません。
“ANOVA” をクリックすると、“This design contains aliased terms”(この計画にはエイリアス項が含まれています)という警告ダイアログが再び表示されます。“Yes” をクリックして、エイリアスのリストを表示させてください。結果は前回よりも遥かに良好です:モデル(M)項は、この応答に影響を及ぼすことが殆どありそうにない高次の交互作用のみでエイリアス化されています。
もう一度 “ANOVA” をクリックして内容を確認したら、“Diagnostics” に移動してすべてのグラフを調べてください。次に、 “Model Graphs” をクリックします。交互作用 BE のプロットの見た目は前回と同様です。実際に確認してみてください。次に、少し視点を変えて物事を見ることにしましょう。Factors Tool の “E: Gear” を右クリックして、これを “X1 axis” に指定してください。BE ではなく EB のプロットが表示されるはずです。別の言葉で言い換えれば、軸が反転したということです。グラフの直線が点線になっている点に注目してください。Gear がカテゴリ型因子(High または Low)であることをこれであらわしているのです。前の BE プロットにおいては、B(タイヤ圧)が高低両極の間の任意の水準に適合できる数値型因子であったため、その直線は実線であらわされていました。
6.結論
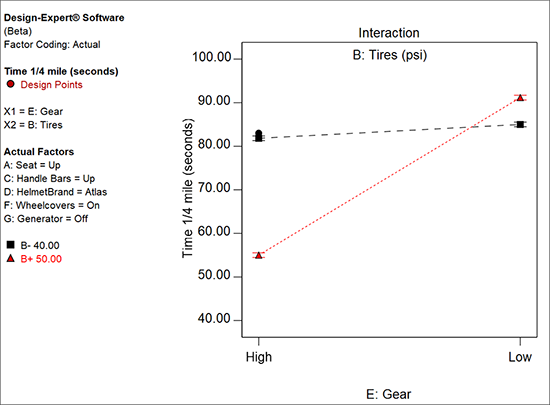
「よい計画のお陰で、実験が上手くいきました!」ランスは大声で叫びました。「ギアを低くした場合は、タイヤ圧がどうあろうと大した問題はありませんが、ギアを高くした場合は、タイヤ圧を高くするほどタイムが伸びることが分かります。」
「同様に、」とシェリルは次のように言います。「タイヤ圧が低い場合は、ギアをどちらにしても実際に大差はないですが、タイヤ圧が高い場合は、ギアを高くする方が良いとも言えます。」
「どっちでもいいよ。」と、ランスはぼやきます。
「あとひとつ気付いたことがあります。」とシェリルは次のように指摘します。「8回の試行の各平均タイムは、回を重ねる毎に増加しています。最初の実験では 70秒だったものが、2回目には 80秒、そして、最後の走行ではほぼ 85 秒にまで落ちています。疲労が重なったと見て間違いありません。このブロック効果を取り出すと良いですね。そうしなければ、思わぬ方向に結論が導かれてしまう可能性があります。」
ランスはこれに同意して「実験計画法って最高ですね。」と言いました。
この事例でランスは、Design‐Expert ソフトウェアから提示された折り重ね技術を使用して、飽和した計画を注意深く拡張させることで、彼が着手した7つの因子から有意な因子を素早く見つけ出し、それらの交互作用を突き止めました。最終的に彼が実施した実験は、3つのブロックに分解される合計24回の試行で済みました。本来であれば、すべての主効果と2因子交互作用が他の主効果や2因子交互作用から制約を受けない分解能 V 計画によるアプローチで分析に着手すべきだったでしょうが、MR5 計画(これは Stat-Ease 社によってのみ提供されます!)を用いたこのアプローチでは、実験を少なくとも 30回は行わなければなりません。古典的な2水準一部実施計画(27‐1)を普通に使ったとしたら、これよりも更に多い64回の試行が必要です。そして、忘れないでいただきたいのは、ランス・レッグストロングが実際に8回走行して得た最初の実験結果がなければ、新春自転車競技大会で現に優勝することもできなかっただろうということです。
この事例でランスは、飽和した分解能 III 計画を用いて勝利の組み合わせを見出しました。従って、彼は実験計画法で当座の問題を解消できたことになります。しかし、彼の友人で個人的コーチでもあるシェリル・ソングバードの後押しがなければ、ランスは折り重ねに必要な追跡実験を成し遂げることも、そして、速度向上に寄与する正確な原因を突き止めることもできなかったでしょう。実験計画法 (DOE) による問題の抜本的解決に、彼女は一役買ったわけです。

