ロジスティック回帰分析における混合成分
1.はじめに
化合物の混合物を分離するプロセスは、クロマトグラフィーと呼ばれます。超高速液体クロマトグラフィー(UHPLC)は、市販のクロマトグラフィー技術において一般的ですが、超高圧を使用するため非常に高価な装置が必要です。
あなたが、ポリマーカラムの開発に取り組んでいる研究者の一人だとしましょう。現在、UHPLCと同等の効率を出すために同様な細孔及び骨格を持ちながらも、低圧力及びはるかな低コストで機能するカラムを開発しています。
問題点:
- 配合によって、完全に固体のポリマー(「均質」カラムと呼びます)が常に作成されるとは限りません。
- 細孔同士は常にくっつき合っていることに注意してください。つまり、分離される化合物はカラムを通って流れません。
最初のステップ:
水、モノマー、及び界面活性剤を混ぜ合わせた際の特性が、目標のカラム(均質で流動性のある)の開発にどのように影響するのかモデル化するために、計画を立て実験をしましょう。
2.実験の計画
カラムの開発に使用されるエマルジョンは、水、モノマー、界面活性剤、および開始剤の混合物です。
- モノマーと水は2つの非混和性の流体であり、界面活性剤は2つの流体の表面張力を低下させる化学薬品です。
- モノマーとは最終的にモノリスの固体構造になるものであり、混合物中の水滴は重合反応中に細孔に置き換わります。この考えは、水が小さな液滴でモノマー全体に十分に分散しているような混合物を作成することです。
研究者は、文献と経験に基づいて混合物成分の条件を決定しましたが、それでもいくらか恣意的な条件になっています。
| Component | Component | Upper Bound | |
|---|---|---|---|
| A | Water | 70 | 86 |
| B | Monomer | 10 | 25 |
| C | Surfactant | 2 | 8 |
| D | Initiator* | 0.02 | 0.25 |
| E | Salt | 0.8 | 0.8 |
| Total = | 100 wt % |
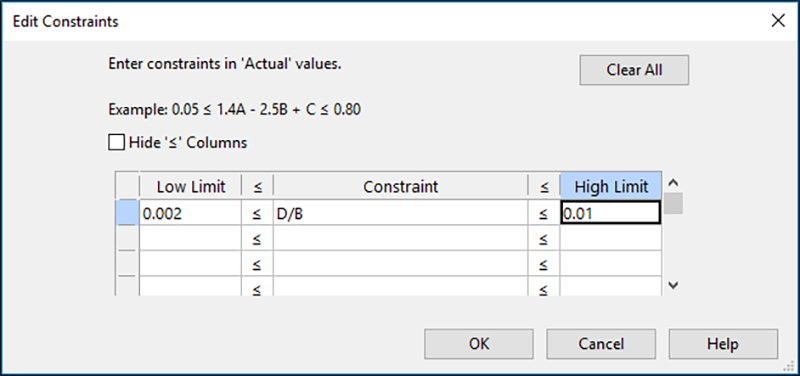
*開始剤はモノマーの0.2%からモノマーの1.0%まで変化します。(0.002≤D/B≤0.01)
バイナリ応答があると、計画の設計方法が変わります。
- 2つの補完的な結果を伴う応答のモデルを推定するには、連続数値応答のモデル化に必要な計画よりも大きな計画が必要です。
- ロジスティック回帰は、独立した入力因子を持つことに左右されます。この制約された混合物の共線性には、より大きな計画が必要です。
- バイナリ応答の場合、スペースを埋める計画を使用することをお勧めします。
- バイナリ応答の場合、複製は必要ありません。
バイナリ応答のため、Design-Expertによって提供される最適な計画のデフォルト設計を変更する必要があります。
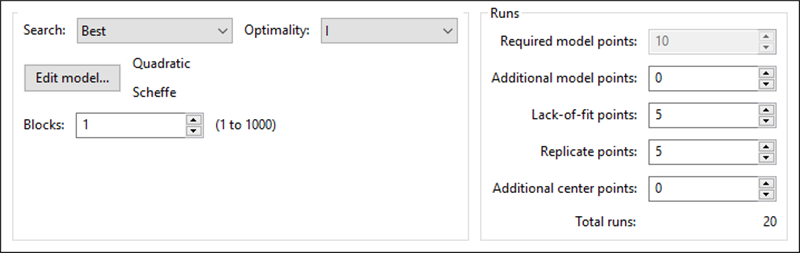
次のように変更します。
- 共線性を克服するために“Additional model points”を追加します。
- スペースを埋めるために“Lack-of-fit points”を追加します。
- “Replicate points”をゼロに減らします。
ここから実際に計画を設計していきましょう。
1) 5成分の最適混合物の計画を選択し、成分と水準を入力します。
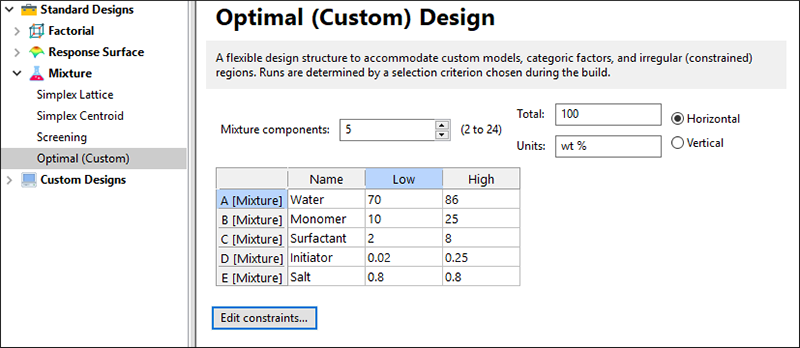
“Edit constraints… ” をクリックして、“Initiator/Monomer”の比率の条件を入力します。
“OK ”、“Next”の順にクリックし進みます。
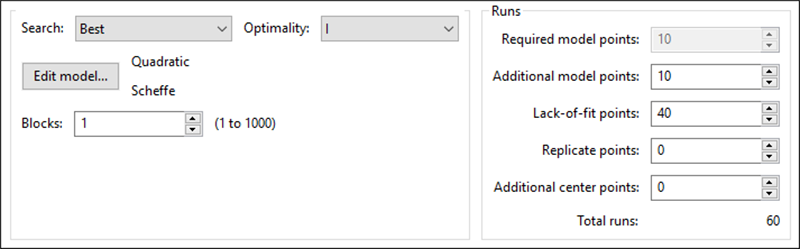
Additional model pointsに「10」、Lack-of-fit pointsに「40」、そしてReplicate pointsに「0」を入力してください。
“Next” をクリックしてください。
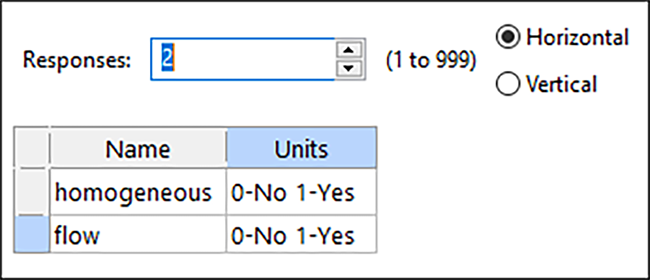
Responsesに「2」と入力します。
“Finish” をクリックしてください。
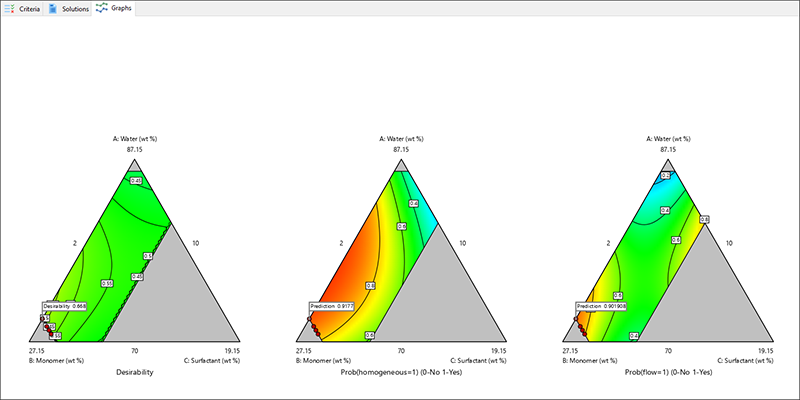
3.結果の分析
新しく応答データを入力する代わりに、“Help” -> “Tutorial Data” メニューから “Polymer Column” を選択することにより、既存のデータを含む計画をロードできます。
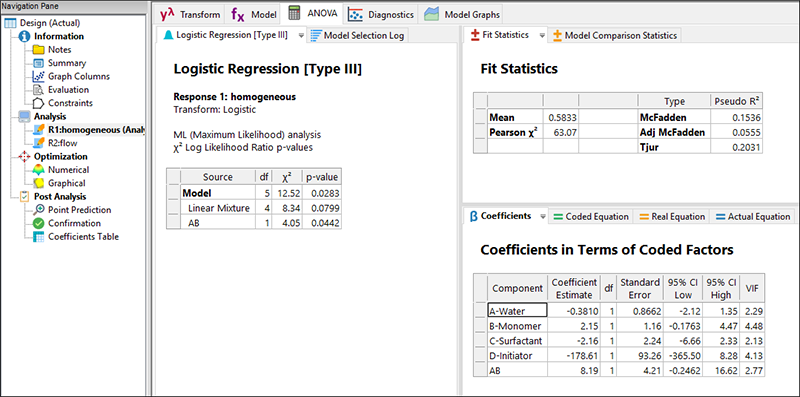
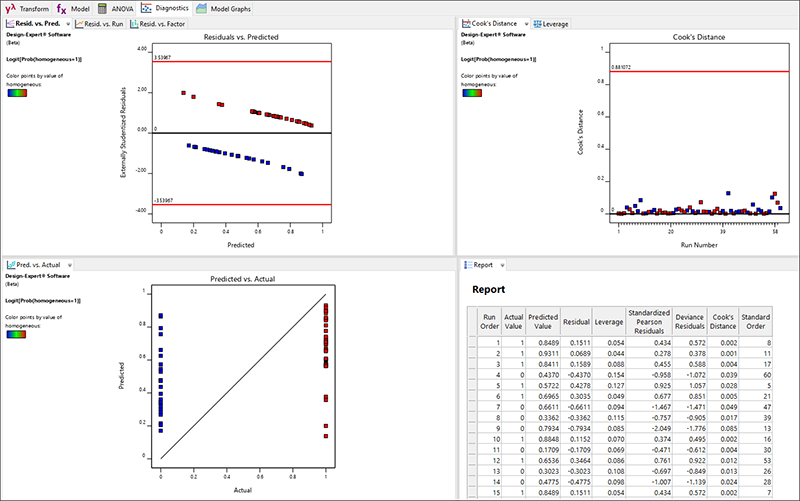
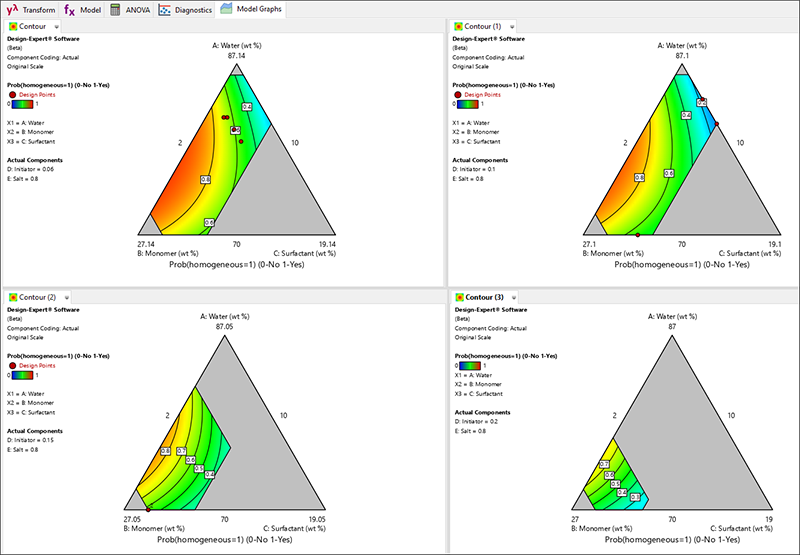
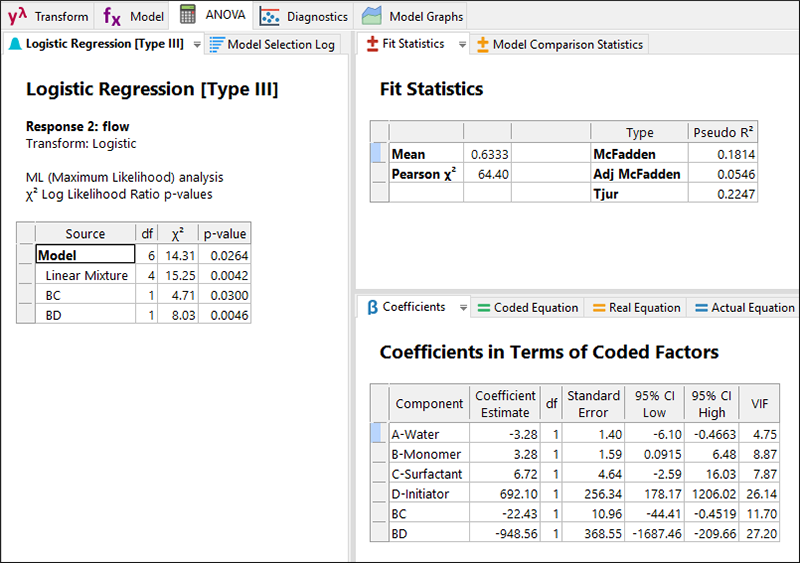
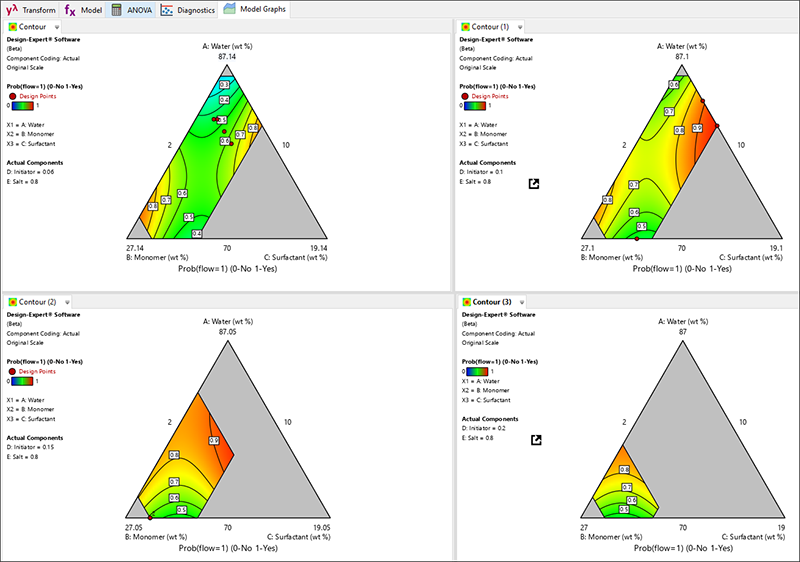
均質(homogeneous)と流動性(flow)はどちらもバイナリ応答です。均質である(1)またはそうでない(0)、流動性がある(1)またはなし(0)として、ロジスティック回帰を使用して分析します。
| ※ 注意 Model タブにおいて “Quadratic” を選択して縮小してみてください。また、AICc criterion において “Backward” を選択してください。 |