RSM に対するヒストリカルデータの適応 (Part 1:基礎編)
1.はじめに
このチュートリアルでは、応答曲面法(RSM)のために用意された Design-Expert® ソフトウェアの回帰ツールを、過去に蓄積したデータに適用する方法を学びます。適切に計画された実験を実施できるのであれば、このような偶然変数を使って実験を行うのはお勧めしません。しかし、どうしてもそれをせざるを得ないのであれば、Design-Expert で予測モデルの構築と応答のグラフ化を簡単に実現できるので、これを活用してください。なお、ここでは、これまでに紹介されたチュートリアルを既にご覧になり、プログラムの多くの機能を習得されているものとして話を進めさせていただきます。少なくとも、『一元配置実験』チュートリアルの基礎編と上級編の両方は、このチュートリアルを始める前に是非ご覧いただくようお願いします。
このチュートリアルで使用する以下に示すヒストリカルデータは、米労働統計局の James Longley によるものです(An Appraisal of Least Squares Programs for the Electronic Computer from the Point of View of the User, Journal of the American Statistical Association, 62(1967): 819-841)。このデータは、RSM Simplified (Mark J. Anderson and Patrick J. Whitcomb, Productivity, Inc., New York, 2005: Chapter 2) でも触れていますが、回帰モデリングに関して興味深い問題を提起します。
| Run # | A: Prices (1954 =100) | B: GNP | C: Unemp. | D: Military Armed Forces | E: Pop. People >14 | F: Time Year | Employ. Total |
|---|---|---|---|---|---|---|---|
| 1 | 83 | 234289 | 2356 | 1590 | 107608 | 1947 | 60323 |
| 2 | 88.5 | 259426 | 2325 | 1456 | 108632 | 1948 | 61122 |
| 3 | 88.2 | 258054 | 3682 | 1616 | 109773 | 1949 | 60171 |
| 4 | 89.5 | 284599 | 3351 | 1650 | 110929 | 1950 | 61187 |
| 5 | 96.2 | 328975 | 2099 | 3099 | 112075 | 1951 | 63221 |
| 6 | 98.1 | 346999 | 1932 | 3594 | 113270 | 1952 | 63639 |
| 7 | 99 | 365385 | 1870 | 3547 | 115094 | 1953 | 64989 |
| 8 | 100 | 363112 | 3578 | 3350 | 116219 | 1954 | 63761 |
| 9 | 101.2 | 397469 | 2904 | 3048 | 117388 | 1955 | 66019 |
| 10 | 104.6 | 419180 | 2822 | 2857 | 118734 | 1956 | 67857 |
| 11 | 108.4 | 442769 | 2936 | 2798 | 120445 | 1957 | 68169 |
| 12 | 110.8 | 444546 | 4681 | 2637 | 121950 | 1958 | 66513 |
| 13 | 112.6 | 482704 | 3813 | 2552 | 123366 | 1959 | 68655 |
| 14 | 114.2 | 502601 | 3931 | 2514 | 125368 | 1960 | 69564 |
| 15 | 115.7 | 518173 | 4806 | 2572 | 127852 | 1961 | 69331 |
| 16 | 116.9 | 554894 | 4007 | 2827 | 130081 | 1962 | 70551 |
このデータ分析を通じて、将来の雇用を景気先行指数 (上記テーブルでラベル A ~ F の付いた因子) の関数として予測することは可能かどうかを調べます。ちなみに Longley が目指したものは、これとは違うものでした。彼が1967年頃考えていたのは、相関関係の高い入力データによって生じる丸め誤差に関する回帰ソフトウェアのテストでした。この困難な目標を、果たして Design-Expert で達成できるでしょうか?様子を見ていきましょう!
それでは、この “experiment” を設定することから着手しましょう(引用符を付けてあるのは、本来の意味の実験とは異なり、どちらかと言えば、偶発的状況におかれたデータの事後的分析であることを強調するためです)。
2.実験の計画
Design-Expert のアイコンをクリックしてください。恐らく、デスクトップ上にあると思います。入力時間を節約するために、データを初めから入力せず、以前に保存した計画を復元します。“Help” -> “Tutorial Data” をクリックして、“Employment” を選択してください。
この計画を復元(どのように作成されたか確認)するには、ツールバーに左側にある空白のアイコン(![]() )を押します。
)を押します。
Design-Expert のダイアログで “Use previous design info?” (前回使用した計画情報を使用しますか?) と表示されたら、“Yes” をクリックしてください。
変更を保存するように求められたら、“No” をクリックします。これで、Custom Designs タブと Historical Data オプションを利用して、この計画がどのように作成されたのか確認できます。
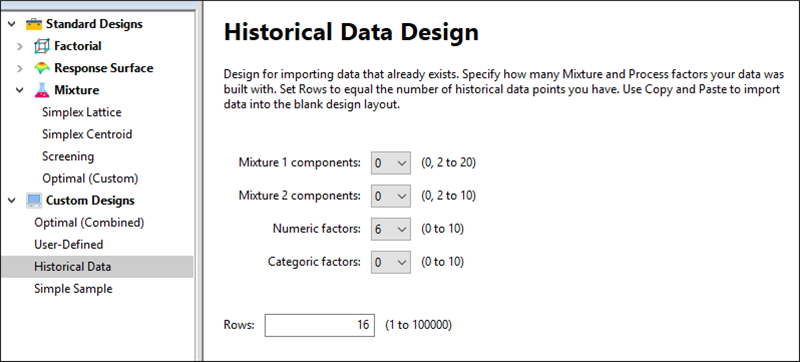
次に進む前に、計画割付表で入力またはコピー&ペーストしたい行数を Design-Expert で指定する必要があります。この事例の場合、Rows の値は 16 になります。
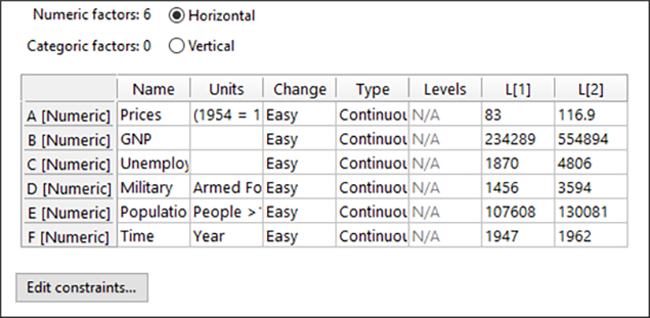
“Next” を押して、因子を表示します。入力した6つの数値型因子のそれぞれについて、名称、単位、および最小(Min)から最大(Max)までの範囲がどのようになっているかご確認ください。“Next” を押して、画面上のすべての入力を受け入れます。
これで、応答の詳細を確認することができます – この場合、応答は1つだけです。
“Finish” をクリックして、試行順に並べられて表示される計画割付表をご確認ください。
データを貼り付ける際の注意点
この時点で、因子水準と実験の結果得られた応答に関する全てのデータを一行ずつ入力していくことも可能です(ご心配なく:このチュートリアルでデータ入力はしません)。しかし、大抵のデータは、スプレッドシード形式であらかじめ用意されていると思います。もしそのようなデータであれば、マウスで範囲を指定してクリップボードにコピーしたあと、Edit -> Paste(または、マウスを右クリックして以下のように Paste を選択)を実行するだけで、Design-Expert の計画割付表に貼り付けることが可能です(以下に示すように、データを貼り付ける前に対象となる全てのセルの一行目を必ずマウスで選択状態にしておいてください)。
空白の実行シートの左上のセルをクリックしただけでは、ひとつの値しか貼り付けることができません。
3.結果の分析
通常ならこの時点で作業内容を保存するところですが、この作業は既に完了していますので、あらかじめ用意されたファイルを単純に開くことにしましょう。“Help” -> “Tutorial Data” をクリックし、“Employment” を選択します。これまでに作業した内容を保存するダイアログが表示されますが、ここでは “No” をクリックして受け入れないでください。
(この事例ではNoを選択)
分析に取り掛かる前に、あらかじめ警告しておきます。これから、最小二乗回帰と分散分析(ANOVA)に関連する統計値を、嫌というほど目の当たりにすることになります。予備知識を持たないままそうなった場合、参考書として RSM Simplified を用意し、いつでも参照できるようにしておいてください。RSM 分析のための統計学については、「Modern DOE for Process Optimization」というタイトルの Stat-Ease 社が開催しているワークショップに参加してください。
Analysis ブランチ下の “Employment” ノードをクリックしてください。応答値を数学的に変換する Transform 画面が Design-Expert に表示されます。しかし、プログラムに表示された注釈にあるように、この事例の応答範囲は非常に狭いため、いずれの変換を適用したとしてもそれによって得られるメリットは僅かに過ぎません。

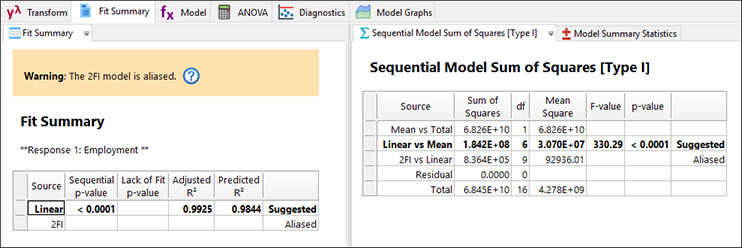
“Fit Summary” タブをクリックします。モデルの各次数が、平均から順に Design-Expert によって評価されます。この事例では線形が実行できる最良の選択です。それより次数の高いモデルはエイリアスになります。
“Model” をクリックして、次に進んでください。
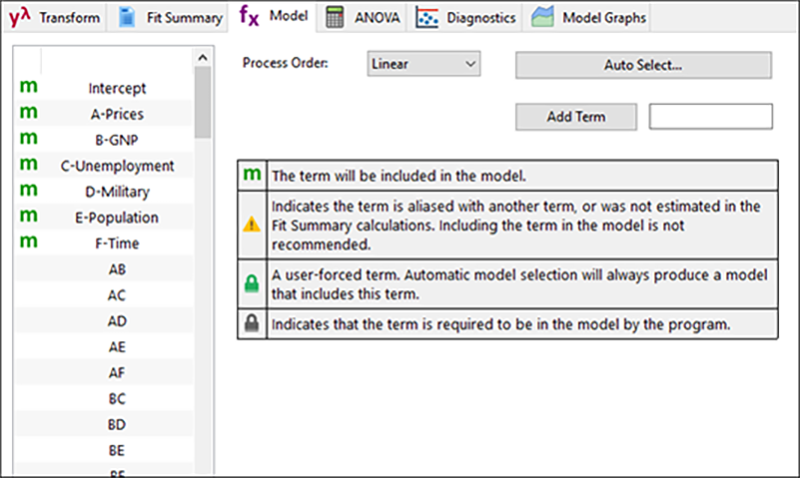
設定内容はいずれも Design-Expert で推奨されたものです。2因子交互作用の多くはエイリアスによって評価対象とされていない点に注目しましょう。感嘆符(![]() )のある黄色い三角形で表されます。驚かないで(このデータはまさに大量の蒸気のように空虚になるからです)、ANOVA(分散分析)ボタンをクリックしてください。
)のある黄色い三角形で表されます。驚かないで(このデータはまさに大量の蒸気のように空虚になるからです)、ANOVA(分散分析)ボタンをクリックしてください。
なお、モデル全体は有意であっても、中には有意でない項も存在する点に注意しましょう。
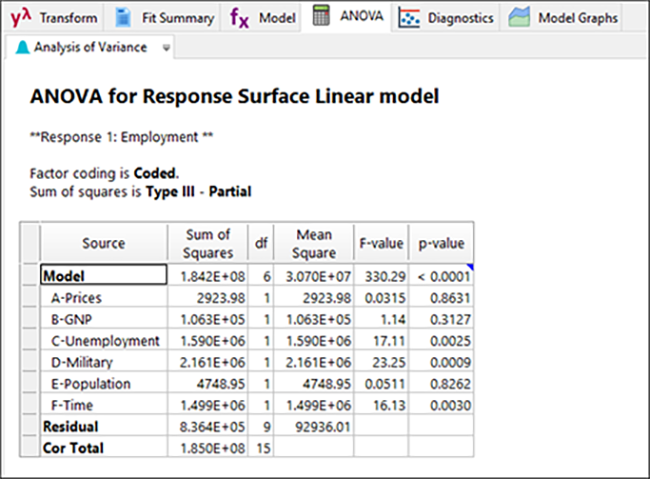
| ※ Design-Expert が実行する分散分析の方法に関する統計学的補足説明 既にお気づきのことと存じますが、この ANOVA には Type III – Partial というラベルが付いています。デフォルトで指定された ANOVA を実行するこのアプローチは、ヒストリカルデータのような非直交配列からなるデータを分析する際、各項の平方和(SS)の合計がモデル全体より少なくなります。各項の SS の合計がモデル全体の SS と等しくなるようにしたい場合は、Edit -> Preferences から Math を選択し、デフォルトの指定を Sequential(Type I)に変更してください。しかし、これを指定すると、第一の項を優先的にモデルに組み入れようとするため、あまり推奨できません。例えば、この事例の場合、偏平方和(Type III – DX のデフォルト)による応答(雇用の合計)に関する ANOVA では、上記に示すように、因子 A の prob>F p-value が 0.8631(F=0.031)と計算されます。結果は有意ではありません。逐次的平方和(Type I)で ANOVA を再計算してみると、p 値は <0.0001(F=1876)に変わります。一見したところ、有意性が高くなったように見えますが、これは、この項(因子 A の主効果)が最初に当てはめられることによるものに過ぎません。この結果は正しくないことが、お分かりいただけると思います。 |
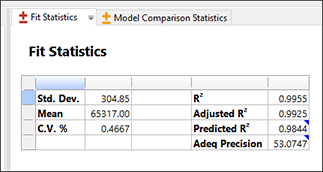
因子 A(Prices)は、デフォルトの ANOVA(偏平方和)の結果で示されているように、全体の中で最も有意性が低いと仮定して、これを除外したらどうなるか見てみることにしましょう。しかし、そのまえに、Fit Statistics ペインに移動して、モデルを減らす前と後で何が起こるかを比較できるようにします。
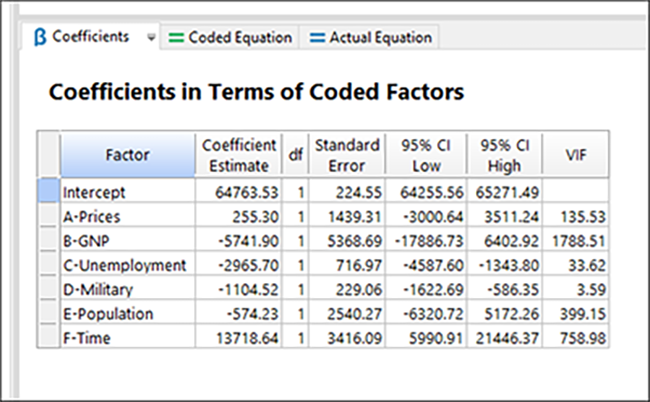
“Coefficients” もクリックして、係数の推定値も確認しておきましょう。
VIF(分散膨張因子:variance inflation factor)の値がとても高い点に注目してください。理想的な VIF 値(配列が直交している場合)は 1 ですが、10 より低い場合は原則として許容されます。因子 B(GNP)のように VIF が 1000 を超えると、モデル係数に重度の多重共線性があることを示します(これは悪いことです!)。次回のチュートリアル(パート2)では、これと同じく Longley データを取り扱いますが、この問題と計画を評価するために、Design-Expert によって出力される他の統計値について更に深く踏み込みます。ここでは、VIF のいずれかの結果を右クリックして文脈依存型の Help にアクセスするか、メインメニューの Help からこの統計値について検索してみてください。詳細な情報が見つかるはずです。
もう一度 “Model” をクリックしましょう。“A-Prices” をダブルクリックして、“![]() ”(モデル)指定を削除し、項を除外します。
”(モデル)指定を削除し、項を除外します。
この段階で、ANOVA に戻り、有意性が二番目に低い項を見つけ出したらそれを除外し、以下同様の操作を繰り返すことができます。しかし、Design-Expert では、この逆行的な除外プロセスを自動的に実行させることができます。そのやり方を次に紹介しましょう。まず、Process Order の指定を “Linear” にリセットします。
次に “Autoselect…” ボタンをクリックします。その後、Selection を “Backward” に、Criterion を “p-value” に変更します。
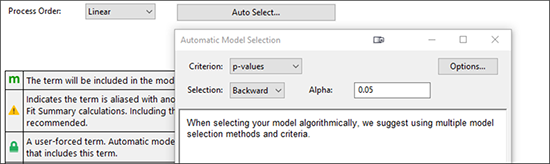
“Alpha out” と書かれたフィールドが新たに表示されます。プログラムのデフォルトの指定では、危険水準(統計学ではこれをギリシア文字のアルファで表記します)が 0.1(p 値によって判定)を超えるまで、有意性が最も低い項を順番に削除していきます。デフォルトの指定をもう少し手堅くしましょう。Alpha out の値を「0.05」に変更します。
“Start” をクリックして、どうなるか確認してください。
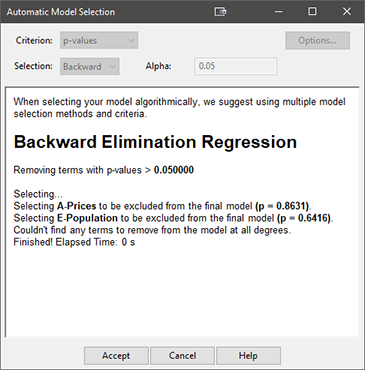
自動選択の内容が逐次的に表示されます。必要があれば、上にスクロールしてその内容を確認することができます。ただし、この場合は先に進んでどのモデルが残ったか、そして、ユーザーフレンドリーな “selecting log” をチェックして、行われた内容を確認します。Start ボタンが Accept ボタンに変わるので、これをクリックしてから ANOVA をクリックして、結果のモデルを表示します。
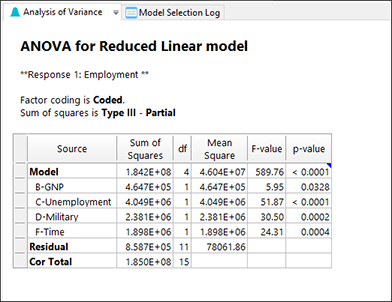
手動で行ったものと同じモデルが残りましたが、こちらの方がはるかに簡単です。ここに至るまでのサマリーを確認することもできます。“Model Selection Log” ペインをクリックしてください。
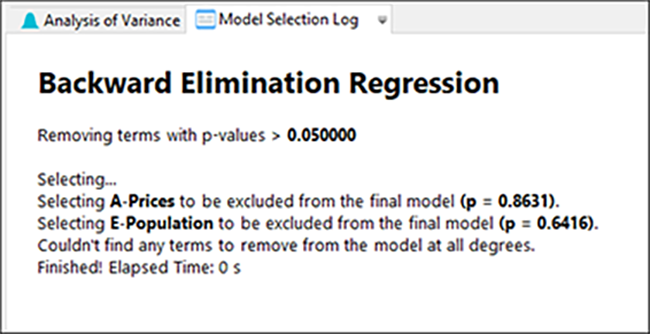
プログラムは予想した通り、初めに A を削除し、その次に E を削除しました。以上で終わりです。以下の ANOVA 表を見て、A、E 以外の全ての項が有意になった点に注意しましょう(注記:レポート内で Model に “significant” と表示されていない場合は、View メニューから Annotated ANOVA を選択して注釈表示を有効にしてください)。
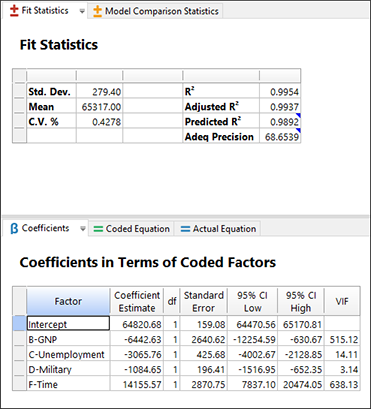
既にお気付きかも知れませんが、モデル全体において、因子 B の p-value は上記に示した値よりもずっと高くなっています。この不安定性は、ヒストリカルデータをベースとするモデルにおいては良く起こることです。“Fit Statistics” ペインと “Coefficients” ペインに移動します。
それでは次に、別の回帰アプローチを試してみることにしましょう。一番上の項(全ての項が選択された多項式にある状態)から順に取り崩していくのではなく 、今度は、モデルを基礎(平均)から作り上げていく方法です。“Model” ボタンをクリックしたら、Process Order を “Linear” にリセットし、“Auto Select…” ボタンをクリックしてください。今回は Criterion として “p-values” を選び、Selection は “Forward” のままにします。この Forward アプローチと、先に実行した Backward とを比較する上で公正を期すために、Alpha の値を「0.05」に変更します。
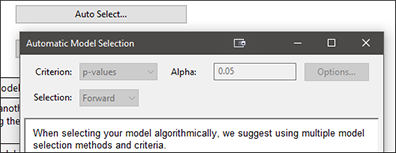
(最初にモデルを元のプロセス次数に戻すことをお忘れなく!)
プログラムに表示されたテキスト(When reducing your model…)の内容に、注意してください。この事例のような共線性の高い因子集合では、このアプローチではうまく機能しないこともあるからです。Start を押してから、“ANOVA” をクリックして現在の状況を確認してみましょう。
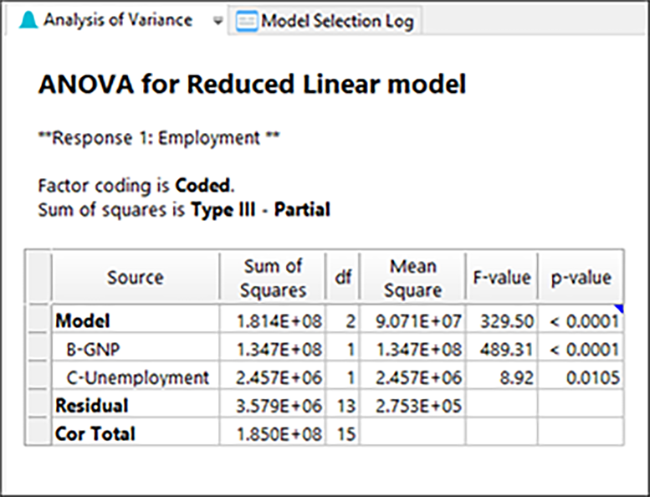
驚くことに最も有意な単一因子として、因子 B が初めに表示されています。その次に因子 C が来ています。以上で終わりです!二番目に有意な因子が有意性を表す alpha-in の閾値 p<0.05 を満たしていないのは明らかです。
“Fit Statistics” ペインに移動します。
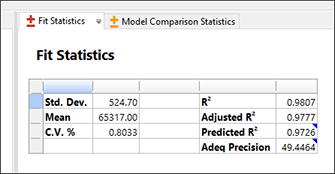
単純になったこのモデルでは、R-squared の尺度でいずれも非常に高い値を示していますが、後方回帰で得られたモデルの値に比べると僅かに劣っています。
最後に “Model” に戻って、Process Order を “Linear” にリセットします。それから “Auto select…” に移動して、Design-Expert によってモデルの最後に示された Selection オプション: “Stepwise” を試してください(基準には必ず p-value を選択するようにしてください)。AIC とBIC は、今後チュートリアルで使用する新しいモデル基準なので注意してください。
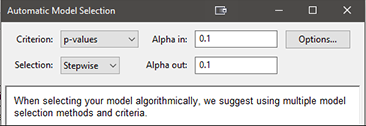
現在画面に Alpha in と Alpha out の両方が表示されていることから推測できるように、ステップワイズアルゴリズムは、基本的に前方選択の要素と同じですが、正確な判定を行うために後方の要素が一部付け加えられています。詳細については、プログラムの Help を検索してください。ただし、ある項が Alpha in の検定を(前方回帰を介して)通過したとしても、その後 (更に項が追加された後) Alpha out の検定 (後方選択) によって処分される場合があること考慮してください。これに違和感がある方は、因子 B の p-value がどのように変化してきたか振り返ってください。この前方選択の手法によって何が起こるのか確認するには、“Start”、“Accept”、“ANOVA” の順に再度押してください。結果は、Alpha in と Alpha out の設定内容によって変わります(デフォルトで用意された値はいずれも 0.1000)。デフォルトでは、この手法により Backward 選択と同じモデルが選択されます。
Forward と Stepwise(基本的に Forward を改良したもの)の両アプローチで表示されるメッセージからもお分かりの通り、自動的な選択法を使用するとすれば、Backward アプローチを選択することになります。そもそも分析に関わる人は、懸案となっている事項の専門家であるか、あるいは、そのような人物といつでも連絡を取れる人であるのが理想です。マニュアルによる手法でモデルの縮小に取り組むことができるのは、まさにそのような人です。その場合、統計結果だけでなく、システムに関する深い知識を有する人が持つ常識的な見解が、誤った判断を防止するフィルタとなるでしょう。
Longley のデータセットを探索するチュートリアルのパート1は以上で終わりです。パート2では、Design-Expert の診断機能にある興味深い残りの分析について、さらに深く掘り下げます。また、Design Evaluation にある高度なツールを使って、どのような情報が収集できるかについても確認します。
