一元配置実験 (Part1:基礎編)
1.はじめに
このチュートリアルでは、Design-Expert® ソフトウェアを用いて一般的な多水準カテゴリーにおける一元配置実験を計画します。このタイプの計画は、次のようなカテゴリー型処理の単純比較を行うのにとても役立ちます
- 一番の供給源はどこか
- 選ぶべき素材はどのタイプか
- 書類の処理の手順を変更したときに何が起きるか
お急ぎの方は、枠で囲んだセクションをスキップしてください。時間をかけてゆっくり学習したい方は、この補足事項をお読みください。
| ※ 応答曲面法について:時間のように連続した因子(その水準を任意の数値に調整可能) を使って実験をしたい場合は、応答曲面法(RSM)の使用を検討してください。これについては、後ほどチュートリアルにて説明しています。 |
この事例で使用するのは、Stat-Ease 社のボウリング・チームが作成したデータです。Pat、Mark、Shari の3人のボウラーが選手枠の最後の1つをめぐって競ったものです。彼らはそれぞれ6ゲームずつボウリングをプレイしましたが、プレイする順番については適正な実験を遂行するために無作為順としました。結果は次とおりです。
| Game | Pat | Mark | Shari |
|---|---|---|---|
| 1 | 160 | 165 | 166 |
| 2 | 150 | 180 | 158 |
| 3 | 140 | 170 | 145 |
| 4 | 167 | 185 | 161 |
| 5 | 157 | 195 | 151 |
| 6 | 148 | 175 | 156 |
| Mean | 153.7 | 178.3 | 156.2 |
チームのキャプテンは、単純に平均スコアの最も高い選手を選ぶだけでは実験の正しい評価ができないことを良く承知しています。キャプテンに要求されるのは、各選手の平均スコアに各ゲームの個別変動がもたらす有意差が存在するかを調べることです。Mark のスコアが最も高いのは偶然の可能性があるかも知れないからです。
この1因子の事例は、単純比較の実験計画(DOE)を実際に利用するための入門に最適です。Design‐Expert ソフトウェアに用意された便利な機能の多くをここで習得できます。
| ※ その他の参考資料について:この演習に示されている機能の全ての説明は、この後のチュートリアルでもその殆どを追って紹介していく予定ですので、ここでは割愛させていただきます。その他の機能や出力結果につきましては、HELP にて詳しく説明されています。メインメニューにある Help をクリックするか、マウスの右クリックや F1 キーによって、文脈に依存した内容のヘルプを表示させることができます。 |
2.実験の計画
Design‐Expert のアイコンをダブルクリックして、プログラムを起動ください。
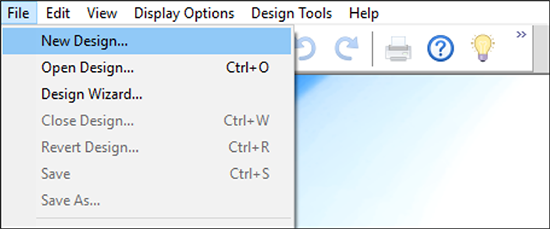
メインメニューの “File” をクリックして “New Design” を選択するか、ツールバーの ![]() アイコンをクリックしてください。
アイコンをクリックしてください。
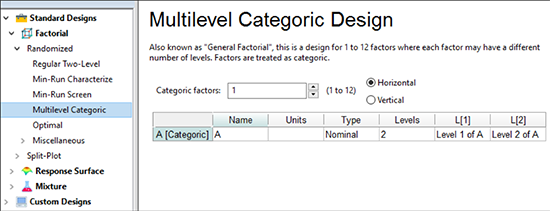
画面左側のツリーに、デザインオプションが表示されます。 Factorial カテゴリーはデフォルトで表示されます。このチュートリアルでは、 “Multilevel Categoric” を選択します。
| ※ 因子を変更するのが難しい場合について:因子のいずれかを制御するのが非常に難しい場合、つまり無作為の水準で簡単に試行できない場合は、 Split-Plot の Multilevel Categoric 計画を検討してください。 ただし、無作為化に制限をかけると、それだけ実験の検出力(Power)に大きな影響が及びますので、なるべく全ての因子が試行の度に偶然による支配で変化するよう工夫してください (Design-Expert のデフォルトでは、試行順を無作為化して計画が配置されるよう設定されています)。 |
計画パラメーターの入力
因子数は、デフォルトで指定された “1” のままにします。
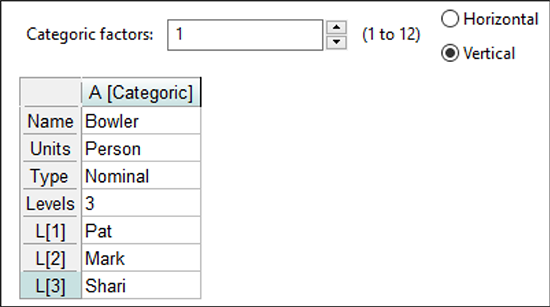
因子の Name には「Bowler」と入力します。Tabキーを使って Units フィールドに移動したら「Person」と入力してください。
Tabキーで Type に移動します。
Typeはデフォルトの「Nominal」のままとし、TabキーでLevelsフィールドに移動し、「3」を入力します。
L[1]~ L[3] の名前として、「Pat」、「Mark」、「Shari」と入力します。
| ※ スクリーンチップスについて:因子タイプのオプションに関する詳細な説明を調べたい場合は、ツールバーの電球アイコン ( |
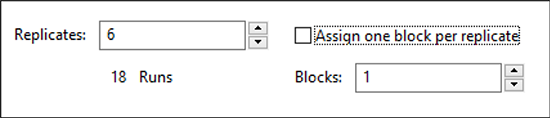
Replicates フィールドに「6」と入力します(各ボウラーが 6ゲームずつプレイします)。TabキーでAssign one block per replicateフィールドに移動しますが、チェックは付けないままにします
“Next”をクリックしてください。簡単なことから始めましょう。 Responses の数はデフォルトの “1” のままにします。Nameのボックスをクリックし、 「Score」 と入力します。 Tab キーで Units フィールドに移動し、 「Pins」 と入力します。
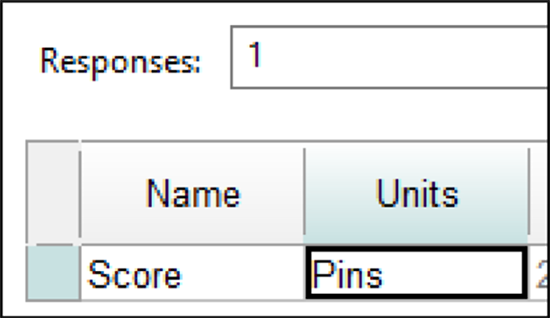
この段階で、残りのフィールドは空白のまま飛ばして、次に進めても構いません。しかし、ここで計画した実験の Power を調べてみることは良いことです。この事例の場合、ボウリングチームのキャプテンは、各ボウラーの平均値を比較して 20 ピンより小さければ差はないものと考えていますので、以下に示すように、Diff. to detect Delta (“Signal”) のフィールドに値「20」を入力しましょう。次に、 Est. Std. Dev. Sigma (“Noise”) の値には 「10 」 と入力してください(これは、典型的なボウラーのバラツキとして過去のリーグ記録を元に導き出された値です)。以上を元に Design-Expert は、Signal/Noise Ratio S/N 比を2と計算します(20 を 10 で割った結果です)。
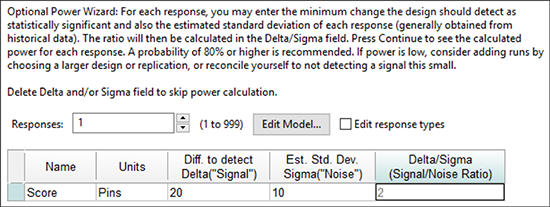
“Next” をクリックすると Power (検出力) の結果が表示されます。期待する差(20ピン)を見分けられる確率が 80% 以上と表示されます。
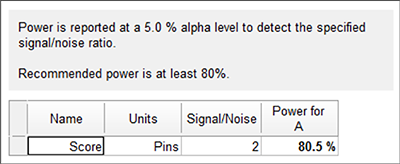
Finish をクリックして、Design‐Expert で計画を作成し、計画割付表(Design Layout)ウィンドウに進みます。
※ インターフェースについて:次に進む前に、Design‐Expert に装備された独自のツリー構造インターフェースを見ておきましょう。ここで、実験の計画と分析を行い、結果の最適化を行います。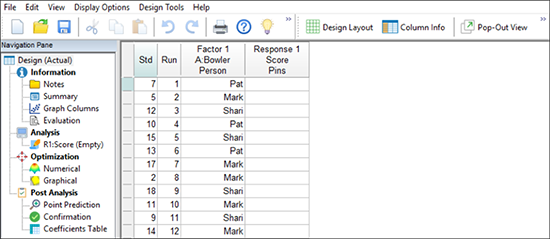 この一連のチュートリアルや、処理の最適化のための応答曲面法などさらに高度な機能に進む中で、いくつかのツリー構造を見ていくことになります。 |
計画の保存
計画の設定が終わったら、“ File” -> “Save As” を選んでファイルに保存することができます。*.dxpx 形式で保存されるデータファイルに保存します (このチュートリアルでは Bowling という名前を推奨します) 。
“Save”をクリックします。
3.応答データの入力
実際に実験を行う場合は、外に出て実測データを収集することになります。ここではプログラムを “File” -> “Exit” で一旦終了させ、これを仮に行うことにしましょう。保存を促されるので、“Yes”をクリックします。Design-Expert を再起動し、“OPEN DESIGN”を選び、 (または、ツールバーの![]() アイコンをクリックします) 、前に保存したデータファイル (
アイコンをクリックします) 、前に保存したデータファイル (Bowling.dxpx) を開きます。画面には表形式でランダムに配置されたデータが表示されるはずです。この例では、ボウリング選手を一致させるために適切な順でデータを入力する必要があります。これを行うには、列ヘッダー Factor 1 (A: Bowler) を右クリックし “Sort Ascending” を選択します。
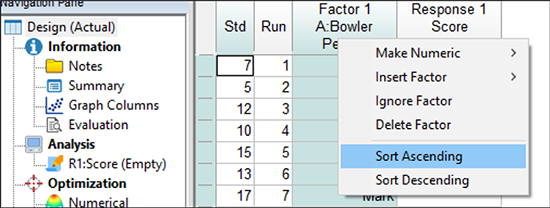
| ※ クイックソートについて: 列ヘッダーをダブルクリックしてもソートできます。 |
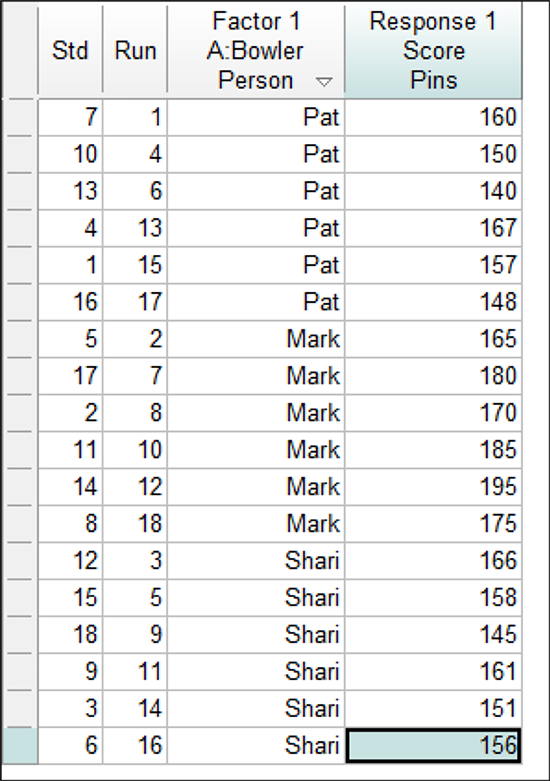
最初のページにあるテーブルを元に応答値を入力してください。または、以下のスクリーンショットを使用しても構いません。計画割付表ウィンドウは、試行順を除いて、次のようになっているはずです。
実際に実験を行う場合、試行と応答の入力は無作為順で行うようにしてください。標準の順番は、予め用意された計画データを簡単に入力する用途以外には使用しないでください。
| ※ 実際の試行順どおりにすることの利点: 数字こだわる方であれば、手元の試行番号を上記と同じ内容に置き換え(上書き)、ボウラーが実際にゲームを行った順番と一致させることができます。ボウリングを6ゲーム行うことは大変ですが、それだけボウラーの真剣さが結果に表れます。しかし、6ゲームの間に短時間の休憩をランダムに挟んでいれば、学習カーブ(進むにつれてうまくなる)や疲れ(時間とともに疲労する)のような時間の経過に依存する影響が排除されます。 |
メニューから“File” -> “Save”を選んで、データを保存します (またはツールバーの ![]() をクリックします)。これでデータが台無しになってしまったときでも、バックアップがあります。このバックアップは重要です。これから計画割付表内で多くのメリットがある機能を試していくためです。
をクリックします)。これでデータが台無しになってしまったときでも、バックアップがあります。このバックアップは重要です。これから計画割付表内で多くのメリットがある機能を試していくためです。
例えば、計テーブルの左上のセルを右クリックします。 この操作で表示を変更することができます。 試しに “Comments” を選択してください。
上記のComments列に、8ゲーム実施した後、ボウリングのレーンの運営者がワックスをかけたという注意書き 「Lane re-oiled」 (レーンオイルの掛け直し) を追加しました。Pat のスコアを見ると、その効果は明らかに無視できるものでした。
| ※ 列サイズの変更について: 必要に応じてこれを試してください。コメントの内容が表示幅を越えるときは、ヘッダーの右の境界にカーソルを持って行くと矢印に変わるので、その状態でダブルクリックすると幅が自動的に調整されます。 |
ボウリングの結果をよりよく把握するために、 Response 1 列のヘッダーを右クリックし、“Sort Ascending”を選ぶことで、昇順に並べ替えます。
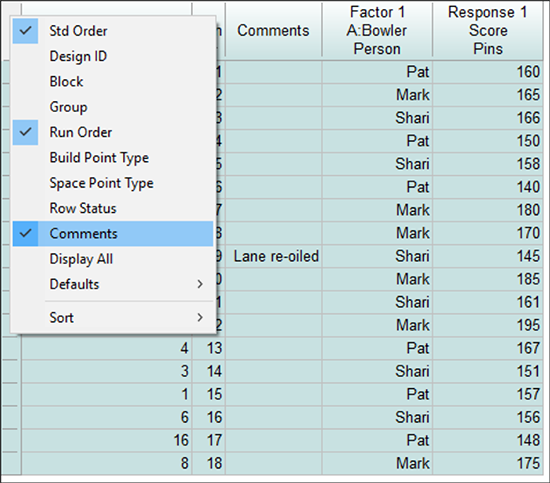
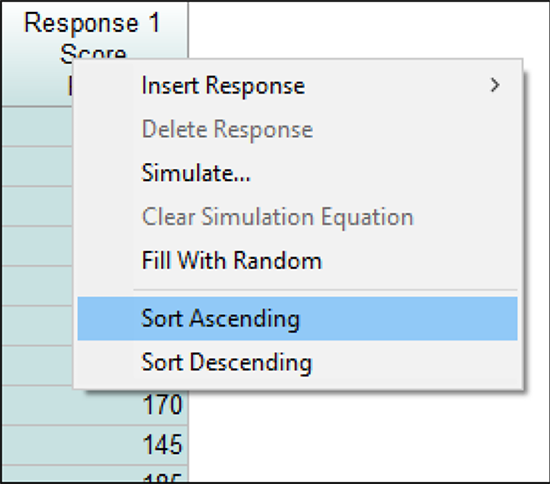
ソートが役に立つ機能であることは分かったと思います。ソートは応答列だけでなく、因子列でも動作します。この例では、ほぼすべてのゲームで Mark が最高のスコアを取ったことが一目でわかります。
4.結果の分析
それでは、データの分析を始めましょう。画面左側のプログラムのツリーから Analysis の “Score” ノードをクリックします。 Transform オプションがメインウィンドウのツールバーに表示されます。これらのボタンを左から右に順にクリックしながら以降の分析を進めていくことになります。作業はとても簡単です。 Transform 画面には、応答の値を変換する機能が用意されています。これにより分析の統計的特性を向上させることができます。
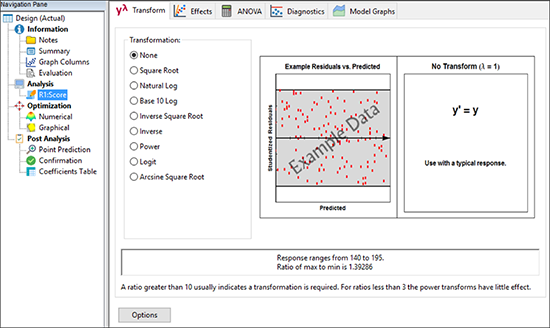
| ※ 変換 (Transformation) の詳細について: 変換の理論的背景を知りたい場合は、まず TIPS を開いてみてください。詳細が必要な場合は、メインメニューの Help コマンドにアクセスして、検索タブで 「transformations」 と入力してください。 |
今回のデータについては、変換を必要としないため、“Effects” タブをクリックして、デフォルトの None のまま先に進みます。
分析の検証
必然的に、チュートリアルは少し統計的な話になります。理解が難しい場合は、回帰に関する基本的な説明会に参加することをお勧めします。さらに良いのは、Stat-Ease社のDOEワークショップに参加することです。
Design-Expert には、因子 A (Bowler) に関する統計誤差 (statistical error)、すなわち、グリーンの三角形が一列に並んで表示されている正常変動と比較して、突発的な効果を強調する非常に特殊なプロットがポップアップされます。
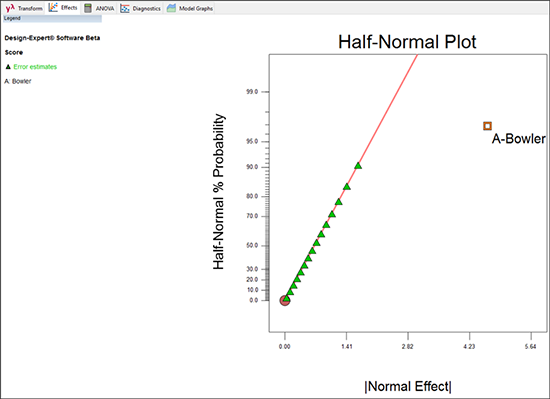
これは、良い結果です。生データの結果から明らかな内容が裏づけされます。まさに、ボールを投げた人物こそが重要なのです。
| ※ 半正規化プロットについて: 効果の半正規化プロットについてさらに知りたい場合は「2水準完全実施要因計画」チュートリアルを参照してください。 |
より詳細な統計結果を表示するには、 “ANOVA”(Analysis of Variance)タブに移動します。表の右端に、結果が有意であることが示されています。
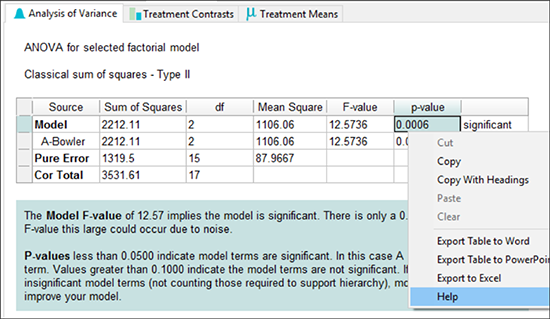
※ ANOVA レポートについて:画面上部のメニューから “View” -> “Show Annotation” を選んで、このオプションのチェック (0.0006 に関する TIPS を表示します (ポップアップメニューの一番下の “Help” を選択します) 。簡単なキー操作で豊富な情報が表示されるので、利用してください。 |
画面の右側の “Fit Statistics” を見て、様々な統計サマリーを確認してください。
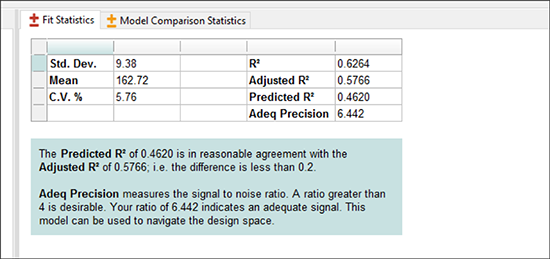
| ※ Post-ANOVA 統計について: これらのサマリー注釈には確認すべき内容が表示され、値を右クリック(または F1 キーを押す)してオンラインヘルプを表示することができます。たいていの場合、特定の統計情報についての役に立つアドバイスを読むことができます。 |
Fit Statistics の下に “Coefficients” ペインがあり、クリックすると次に示すような出力が表示されます。
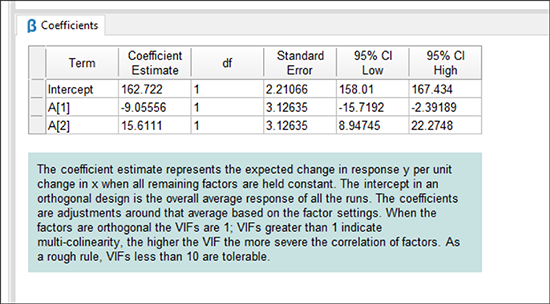
ここでは、各モデル項の係数の算出結果や信頼区間(CI)など統計の詳細を確認できます。1因子を比較するこのような単純な実験では、3人のボウラー全体の単純な平均スコアが切片となります。3人のボウラーに対する予測モデルなのに、A1 と A2 の2つの項しかないのはどうしてか、と不思議に思われる方がいるかもしれません。全体の平均と A3 以外の2人のボウラーの平均値が分かれば、最後のモデル項 A3 はおのずと予測することができるため、これは余分なものとなるのです。
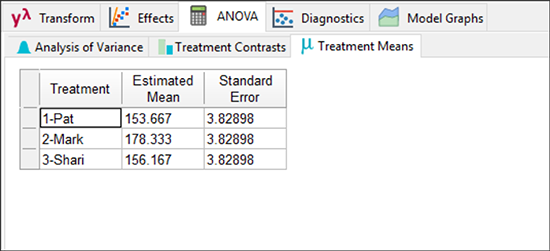
次に、この画面内の次のセクション “Treatment Means” タブに進みましょう。
ここには、3人のボウラーそれぞれの平均が示されています。次に “Treatment Contrasts” タブをクリックすることで、一対毎に t-検定を使って(pair‐wise t‐tests)比較されます。
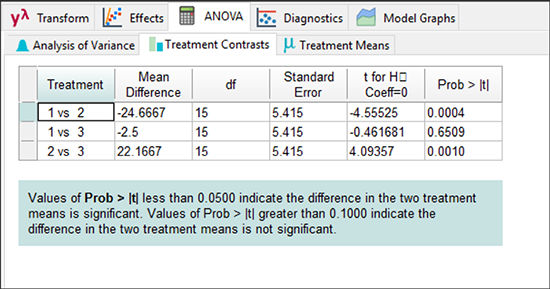
この処理の比較から次のような結論を導くことができます:
- Pat と Mark (1 vs 2) を比較すると、その違いは有意である (24.67 ピンも悪い!)
- Pat と Shari (1 vs 3) の平均 2.5 ピン差は、有意でない(あるいは、ボウリングチームのキャプテンはこれを重要とはみなさない。計画の検出力 (Power) 指定で、最低限の関心は 20 ピン差であったことを思い出してください)
- Mark と Shari (2 vs 3) を比較すると、その違いは有意である (22.17 ピンも良い!)
残差を分析
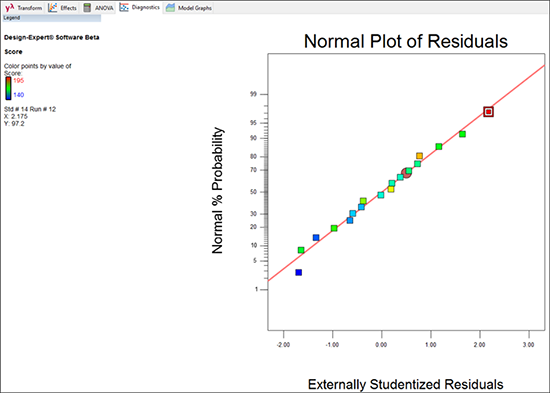
“Diagnostics ” タブをクリックすると、診断プロットが表示されます。レイアウトツールバーで、残差の通常のプロットを最大化するために単一の分割アイコンを選択してください。

このプロットはラインが直線となり、ラインから外れる異常値が一切ないのが理想的です。
| ※ 鉛筆検定について: 手元に鉛筆(あるいはまっすぐなものであれば何でも)があれば、それをグラフにあててみてください。全ての点がだいたい覆われているでしょうか?この事例の場合、答えは Yes となります(正規性を調べる鉛筆検定はこれでクリアです)。赤の細いラインとそのピボット・ポイント(中央の赤い丸)は、マウスをドラッグすることで位置を変更することができます(マウスポインタをライン上に移動して、左ボタンを押しながらマウスを動かします)。ただし、ラインの位置をあえて変更するのはお薦めしません。基本的にプログラムが自動的に理想的な位置にラインを配置してくれるからです。ラインの位置を元に戻したい場合は、マウスの左ボタンをグラフ上でダブルクリックするだけでリセットできます。 |
各点は応答の水準に応じて、色分けされている点に注目してください:青色が最も低い値で、赤が最も高い値です。この例では、赤い点は Mark が最高の 195 ピンを記録したゲームです。ここで、Pat と Shari は、Mark が 195 ピンを獲得したこのゲームは極端に高すぎるので捨てるべきだと考えています。この言い分は正当でしょうか?この赤い点をクリックして、それだけを強調表示させた状態のまま、Diagnostics Tool(Diagnostics タブの上にある青いレイアウトアイコンから、一度に表示されるグラフの数を選択)を使って、残りのグラフを見ていくことにしましょう。
195 のゲームをハイライト)※ Diagnostics ツールのドロップダウンリストについて: Diagnostics Tool ではデフォルトで “Studentized” にチェックが入っている点に注意してください。これは、オリジナルの単位(この事例ではボウリングの「ピン」)でレポートされた残差の生データを、標準偏差に基づく無次元数に変換するものです。尺度は、プラスとマイナスになります。スチューデント化の詳細はヘルプをご覧ください。Diagnostics Tool の下に表示されたロックダウンリスト内の選択を外せば残差の生データを表示することができます。実際にお試しください! 表示する残差の選択肢 ただし、試行に大きなレバレッジ(また統計用語が出てきたので、ヘルプを参照してください)がある場合は、残差をスチューデント化しなければ有効な診断グラフを得ることはできません。例えば、この事例で仮に Pat と Shari が Mark のハイスコア・ゲームを巧みに排除できたとすれば(実際はそうなりませんので、ご心配なく!)、Pat と Shari の各 6 ゲームのレバレッジはそれぞれ 0.167(1/6)であるのに対して、1ゲーム分排除された Mark の5ゲームのレバレッジはそれぞれ 0.2(1/5)となってしまいます。レバレッジにこうした不均衡が生じることのないよう、スチューデント化機能を常にオン(デフォルト指定のまま)にしておくことをお薦めします。そのため、現在 Residuals を選択している場合はデフォルトで表示される元の選択に戻してください。*P.S. デフォルト設定における残差の表示は “外的に(externally)” 行われているという側面もあります。詳細は、「2水準完全実施要因計画」チュートリアルを参照してください。とりあえず今は統計的残差にさらに大きな検出力を提供するためにプログラムはこの形式を選択するということのみの知識で十分です。これにより、さらに Mark のハイスコアに注目せずにはいられなくなります。 |
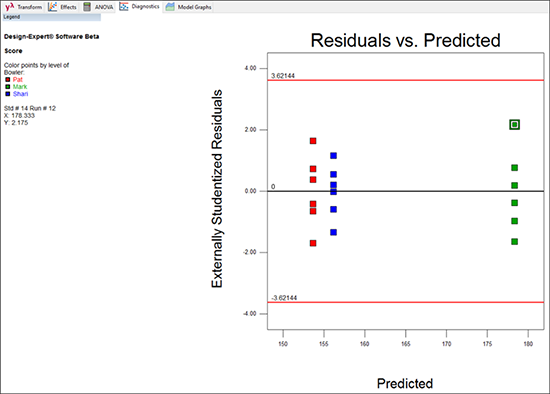
次に、“Resid. vs. Pred.” タブを選択して、個々のゲームの残差と応答モデルによって予測されたグラフを見てみましょう。
| ※ 真偽の怪しい話について:“residuals” は、恐らく統計学者によって “error” と呼ばれるようになったのでしょうが、品質管理の人々は、これによって生じる誤解が多いことに不満を抱いています。 |
どの残差がどのボウラーであるかを区別しやすくするには、診断ツールの Color By オプションのメニューから “Bowler” を選択します。
スチューデント化された残差は、その予測値とは無関係の大きさになります。言い換えると、スチューデント化された残差の縦方向の幅は各ボウラー間でほぼ等しくなるということです。この事例のプロットを見ると、問題は特になさそうです。Mark のゲームだけ全体として右に離れていますが、これについては驚く必要はありません。最高スコア(強調表示している点)を排除せよという申し立てがありましたが、下から上への縦方向の変動幅は、他の2人のものと比べて特別に突出しているわけではありません。
次に、 “Resid. vs. Run” タブのグラフを見てみましょう(注意:実際のグラフは無作為化により異なる場合があります)
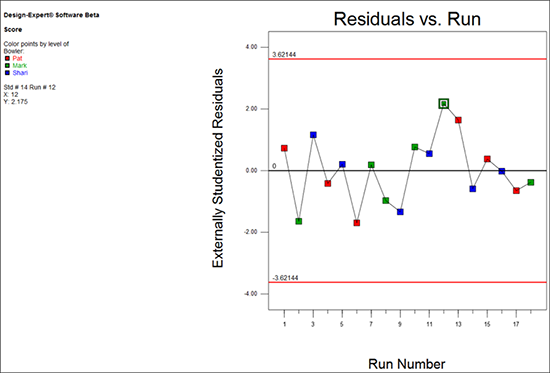
このグラフでは、ボウリング場の状況(例えば、レーンのワックス塗り直し)、ボウラーの疲労、その他の時間と共に変化する隠れた変数によってもたらされる傾向が読み取れると思います。
| ※ 可能性のあるトレンドの影響について: この事例に関しては、特に問題はなさそうです。仮に極端な変動が上下に確認されたとしても、この実験の試行は完全に無作為化されているため、結果にバイアスがかかることは殆どないはずです。実験が制御されない変数によって妨害されるのを確実に防ぐには、常に無作為化を行うよう心がけてください! |
この場合さらに重要なのは、すべての点が(95 パーセントの信頼水準で計算された)範囲内におさまっていることです。 Mark の最高スコアのゲームの突出は、一般に想定される変動に過ぎないということです。従って、これを特に不適格であると見なす理由はありません。
5.平均とデータ・プロットの表示
分析の順序に並んだツールバーから “Model Graphs” タブを選択してください。応答の全データと、処理(因子)毎の各水準の平均値がプロットとして表示されます。このプロットでは、因子毎の各水準を平均したデータとその効果、および、応答の幅を一目で見ることができます。このとき Y 軸は、実際のデータに合わせて自動的に 140 から 10 ピンおきに 200 まで縮尺されている点に注目してください。
この効果プロットの四角い点は、因子水準(A: Bowler)毎の予測応答をあらわします。縦方向に伸びる I 型のバーは、処理毎の 95% LSD(最小有意差)区間をあらわします。Mark の LSD バーは、Pat や Shari の LSD バーと水平方向に移動しても重なりませんので、少なくとも 95% の信頼度で、Mark の平均は他の二人のボウラーの平均よりも高いことが有意であると言えます。
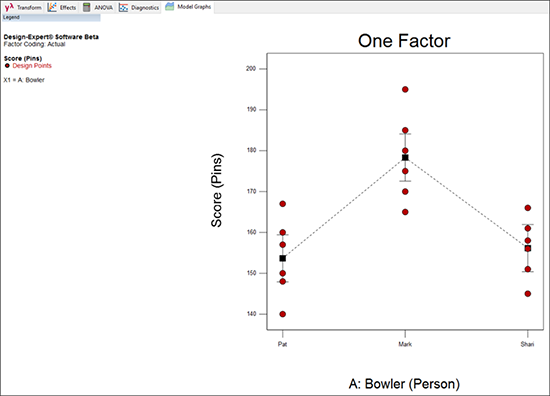
| ※ モデルグラフにおける個々の比較について: LSD バー中央の平均を表すボックスのいずれかをクリックすると、対比較がグラフィカルに表示されます。強調表示した点の予測平均を、通る水平線が描画されます。水平線と交わる任意の垂直バーは、選択した点と有意差がない予測平均を表します。また、凡例には、どれが有意差のある平均かをテーブルで表示されます。なお、表示される対検定は両側検定ですが、解釈しやすくするように、表示されるのはその間隔の半分となります。 |
Pat と Shari の LSD バーについては、水平方向に移動すると重なり合いますので、二人のうちどちらが優れているかは何とも判断できません。二人ともボウリングのマイナーリーグで修行したあと、一年後に改めて試合を開き、能力に有意な差が見られるかを試すのがよさそうです。一方、Mark はこの試合で記録した高い平均スコアから、自分が Stat‐Ease のボウリングチームの期待に応える選手にふさわしいことを正々堂々と宣言することができます。
今回はここまでにしておきましょう。“File” -> “Save”(または保存アイコン![]() をクリック)で結果を保存してください。ここで “Exit” を選択して Design‐Expert を 一旦終了しても良いですし、このまま次のチュートリアル(一元配置実験(Part 2:上級編)に進んでも構いません。Part2では更に踏み込んだ機能を紹介します。
をクリック)で結果を保存してください。ここで “Exit” を選択して Design‐Expert を 一旦終了しても良いですし、このまま次のチュートリアル(一元配置実験(Part 2:上級編)に進んでも構いません。Part2では更に踏み込んだ機能を紹介します。

