
Q-Chem:技術革新の原動力
Q-Chem は、分子の構造、反応性、振動、電子および NMR スペクトルを正確に予測するための非経験的 (ab initio) 量子化学計算の統合パッケージです。ラップトップまたはデスクトップ、クラスター、またはスーパーコンピューターセンター上の Linux、macOS または Windows で実行することができます。
開発元:Q-CHEM, Inc.
機能一覧
密度汎関数理論
LDA、GGA、メタ GGA、GGA とメタ GGA のハイブリッド、Range-Separated ハイブリッド、ダブルハイブリッド汎関数をサポートしています。基底状態および時間依存 DFT による励起状態について、一点エネルギー、構造最適化、振動計算、その他多くの特性を評価することができます。
電子相関
Møller-Plesset 摂動論や結合クラスター法 (Coupled-Cluster Methods) など、電子相関効果を扱うための最新ツールが用意されています。強い相関のある系に対しては CASSCF、結合クラスター価電子結合 (CCVB)、Selected CI、RAS-CI、Spin-Flip、V2-RDM 法などの特殊な手法が使用できます。
励起状態法
CIS、TD-DFT、NOCI、EOM-CC、ADC といったさまざまな電子励起状態の研究手法が使用できます。これらの手法はさまざまな電子状態をカバーしており、分光学的特徴、電荷とエネルギーの移動、および非断熱ダイナミクスのシミュレーションを可能にします。さらに、波動関数解析モジュールを使用することで、励起状態に関するより深い洞察を得ることができます。
溶媒和と埋め込み
SM8、COSMO、C-PCM などの陰溶媒モデルから、陽溶媒効果を取り扱う有効フラグメントポテンシャル法 (EFP) まで、さまざまな溶媒和系のモデリングソリューションを提供します。さらに、QM/MM や密度埋め込みなどのさまざまな埋め込み手法や、CHARMM および GROMACS へのインターフェースが用意されています。
分光モデリング
さまざまな種類のスペクトルをモデリングするためのツールを利用できます。IR およびラマン分光法、UV-vis 分光法、X 線分光法、光電子分光法、NMR 分光法、非線形分光法 (2 光子吸収法など) を使用することができます。 分光学的特徴は、TDDFT から EOM-CC や ADC 法まで、多くの異なるレベルの理論を用いて研究することができます。
分子間相互作用
ALMO に基づく EDA により、全相互作用エネルギーを物理的に意味のある項に分解し、分子間および結合間相互作用の本質を明らかにすることができます。また、対称性適応摂動論 (SAPT) およびその拡張多体系版 (XSAPT) による分子間相互作用の計算と解析も可能です。
化学反応
幾何学的最適化、ポテンシャルエネルギー曲面スキャン、遷移状態探索、固有反応座標追跡などの手法を提供し、化学反応性、熱化学、化学反応速度論の研究に理想的なツールです。
分子動力学法
NVE および NVT サーマルサンプリングを含む第一原理分子動力学 (AIMD: ab initio molecular dynamics) と、準古典的分子動力学 (QMD: quasi-classical molecular dynamics) を実行することができます。これらのアプローチにより、振動スペクトルや第一原理経路積分を生成することができます。また、非断熱系を効果的に扱うための Tully の最少スイッチ表面ホッピング (FSSH) アプローチも実装されています。
Q-Cloud:クラウドで Q-Chem を実行
Q-Cloud では、Amazon Web Services を通じてクラウド上で Q-Chem の計算を実行することができます。事前に構築されたイメージと使いやすいコマンドラインインターフェイスを提供しているため、すぐに計算を開始することができます。
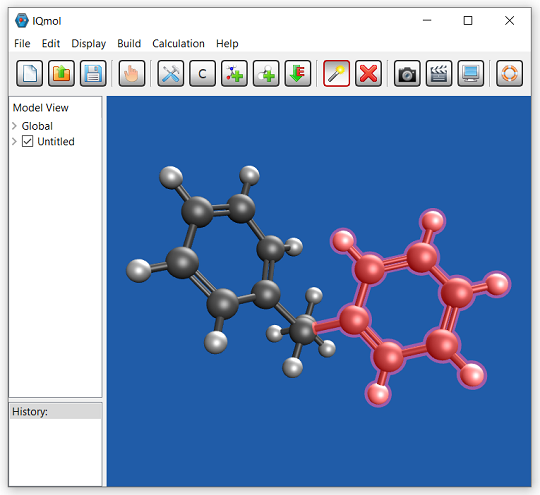
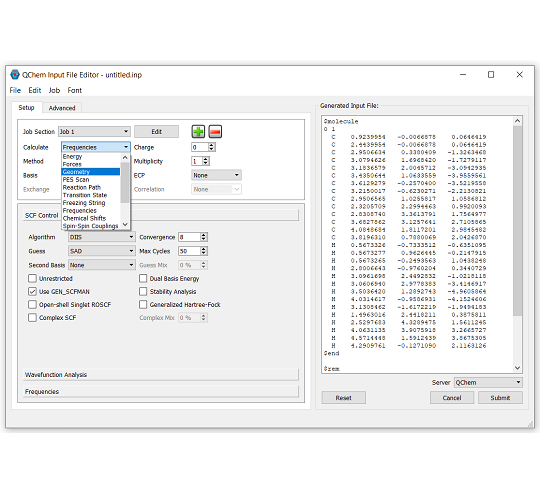
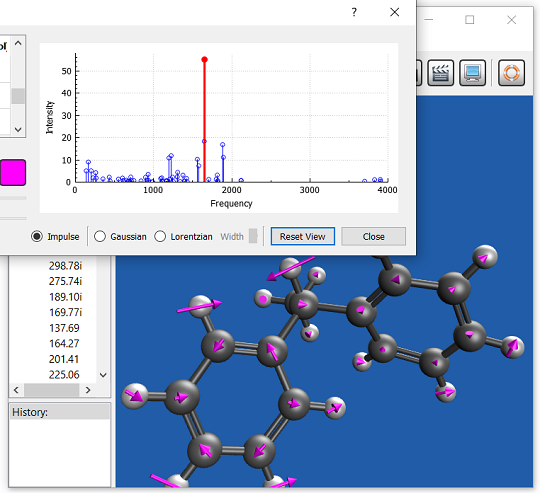
IQmol:Q-Chem 用グラフィカルユーザーインターフェース
IQmol は、オープンソースのフリーな分子エディタおよび可視化パッケージです。分子エディタ、表面生成 (軌道、密度)、アニメーション (振動モード、反応経路) など、さまざまな機能を提供します。IQmol を使用してサーバー上で小規模の Q-Chem の計算を無料で実行したり、IQmol と Q-Chem のローカルインストールをインターフェースで接続することができます。
リリースログ
- v 6.4 で追加された機能
- v 6.3 で追加された機能
- v 6.2 で追加された機能
- v 6.1 で追加された機能
- v 6.0 で追加された機能
- v 5.4 で追加された機能
- v 5.3 で追加された機能
- v 5.2 で追加された機能
- v 5.1 で追加された機能
- v 5.0 で追加された機能
動作環境
OS:x86 64 ビットシステム (Intel、AMD) 上で動作する Linux、macOS、Windows
- Linux
最新の Linux ディストリビューション:RHEL, CentOS, SuSE, Debian, Ubuntu, … - macOS
El Capitan (10.11) 以降
Monterey (12.x), Ventura (13.x), Sonoma (14.x), Sequoia (15.x) を含む
Intel チップ搭載の macOS は、Q-Chem 6.3 以降のバージョンではサポートされません。 - Windows (64-bit)
Windows 8, 10, 11
メモリ:2 GB (CPU コアあたり)
HDD:1.4 GB (インストール時) + スクラッチディスク
インストール時に収集されるライセンスデータ (マシン固有) を Q-Chem 社にメール送信し、 ライセンスキーを発行・入手する必要があります。
ライセンス
ライセンスタイプ
1. Single Research Group ライセンス
1 つの研究グループ内でのみ使用可能。研究責任者 1 名とそのグループメンバーを対象とします。
- Single Seat: 32 コアのノードロックライセンス。32 コア以下のマシン 1 台にインストール可能。
- Cluster: 256 コアのノードロックライセンス。OS 問わず、複数のマシンにインストール可能。マシンの合計コア数は最大 256 コアまで。
- Unlimited: コア数無制限。ノードロックおよび FlexNet ライセンスキーを提供。
Q-Chem ライセンスのコア数は、Q-Chem がインストールされるワークステーションまたはクラスタの CPU コア数以上をご指定ください。
2. Multiple Research Group ライセンス
異なる部門または 1 つの部門から最大 3 つの関連グループで使用可能。コア数無制限で、ノードロックライセンスと FlexNet ライセンスの両方が利用できます。
3. Site ライセンス
1 つのサイトまたはキャンパス内のすべての研究グループを対象とします。
QMP (Q-Chem Membership Program) (年間保守)
Q-Chem は毎年新しいバージョンをリリースしています。ライセンスご購入時に QMP にご加入いただくと、QMP 期間内にリリースされる最新バージョンが提供されます。QMP は後から加入することはできません。
QMP に加入されていない場合は、アップグレードのご購入により最新バージョンをご利用いただけます。
Q-Chem 6.4 へアップグレード可能なバージョンは 6.0, 6.1, 6.2, 6.3 です。 5.4 以前のバージョンをお持ちの場合は、新規でのご購入となります。
トライアル
デモ版の有効期間は 2 ヶ月です。製品版と同じ機能をご利用いただけます。
デモ版お申込み
製品価格
製品価格はお見積りフォームよりお問合せください。
製品補足情報欄に、ご希望のライセンスタイプ (Single Research Group / Multiple Research Group / Site) をご記入ください。
Single Research Group ライセンスをご希望の場合はコア数 (Single Seat / Cluster / Unlimited) もご指定ください。
アップグレードのお見積もりをご希望の場合は、現在お持ちの製品名、バージョン、シリアル (Order number) を必ずご記入ください。
お見積り・ご購入
サポート
インストールガイド
インストール時に収集されるライセンスデータ (マシン固有) を Q-Chem 社にメール送信し、ライセンスキーを発行・入手する必要があります。
マニュアル
- Q-Chem User’s Manual (開発元:英語)
