Boys 法と ER 法による非断熱状態の局所化
Boys and Edmiston-Ruedenberg Localized Diabatization
- 開発者: Joseph Subotnik, Ryan Steele, Neil Shenvi, Alex Sodt
Ryan Steele
 |
|
Neil Shenvi
 |
|
Alex Sodt
 |
|
Joe Subotnik
 |
|
電子移動またはエネルギー移動の速度予測では、安定した非断熱状態の計算が重要となります。この手法では、非断熱カップリング値を計算し、マーカス理論の速度式に導入しています。Boys 法と Edmiston-Ruedenberg 法による局所化は、非断熱状態を系-溶媒の相互作用の物理モデルから説明できるユニークなツールです。フラグメントの定義やその他のパラメータ化は必要ありません。post CIS/TD-DFT 計算にこの機能を適用してください。非断熱励起状態から非対角要素をもつ非断熱ハミルトニアンを作成できます。
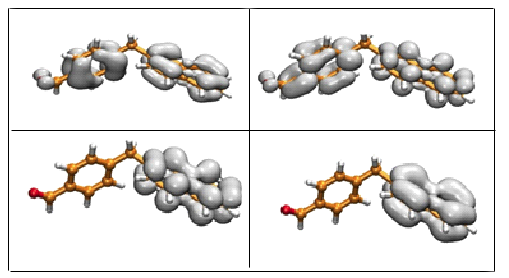
この図は、交点(crossing point)付近における、非断熱および断熱状態での1電子の増加密度および減少密度を示します。非断熱の図で励起子 (exciton) の局所化する様子をご確認ください。
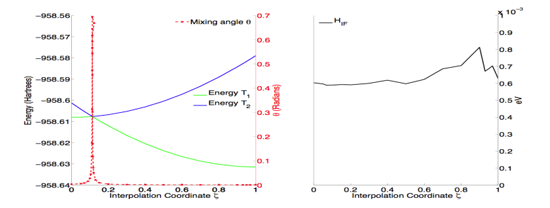
上図は、有名な Closs らが測定した分子の非断熱カップリングを原子核構造の関数として示しています。この非断熱カップリングは核座標の関数としては変化せず、マーカス理論を前提とするいわゆるコンドン近似が正しいことを示します。左側は交差回避 (avoided crossing) をとる断熱的見地から同じ電子状態を説明したものです。
論文:
- J. Subotnik, S. Yeganhe, R. Cave, and M. Ratner, “Constructing diabatic states from adiabatic states: Extending generalized Mulliken-Hush to multiple charge centers with Boys localization” J. Chem. Phys., 129, 244101 (2008)
- J. Subotnik, R. Cave, R. Steele, N. Shenvi, “The initial and final states of electron and energy transfer processes: Diabatization as motivated by system-solvent interactions” J. Chem. Phys., 130, 234102, (2008)
- J. Subotnik, J. Vura-Weis, A. Sodt, M. Ratner, “Predicting Accurate Electronic Excitation Transfer Rates via Marcus Theory with Boys or Edmiston-Ruedenberg Localized Diabatization” J. Phys. Chem. A, 114, 8665, (2010)
- J. Vura-Weis, M. Newton, M. Wasielewski, J. Subotnik, "Characterizing the Locality of Diabatic States for Electronic Excitation Transfer By Decomposing the Diabatic Coupling” J. Phys. Chem C 2010, 114, 20449-20460
Q-Chem 4.0 マニュアル:
計算例