豊富な解析機能を誇るグラフ作成ソフトウェア
Igor Proは、科学者やエンジニアのための非常に強力で拡張性の高いグラフ作成、データ解析、画像処理、およびプログラミングツールです。
科学的および工学的データの実験や、出版品質のグラフおよびページレイアウトの作成のためのインタラクティブなソフトウェア環境です。
こだわりに応えるグラフ作成機能
作成したグラフは EPS 等の画像形式で高解像度で出力・印刷することができます。


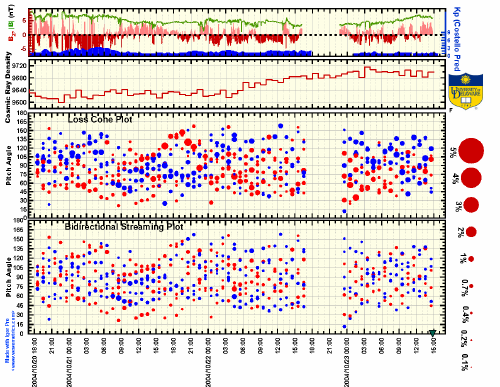
科学・工学分野の豊富な解析機能
回帰分析、フーリエ変換、スムージング、ヒストグラム、スペクトル解析、信号測定、画像解析など多彩な解析を強力に行います。
自由度のある統合科学ソフトウェア
Igor Proを解析処理システムのプラットフォームとして利用することで、”開発工数の削減”と”自由度”を両立したシステム開発が可能です。
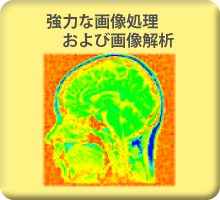
開発事例(1) DataBase連携 –データ処理・保管と保全管理–
【特徴】
- データ処理のフローを独自のルールで定義が可能
- 利用者はDB保存を意識することなく解析業務に集中可能
- DataBase連携を行うことで過去データ検索や精度管理も実現可能(過去集計データからの外れ値判定など)
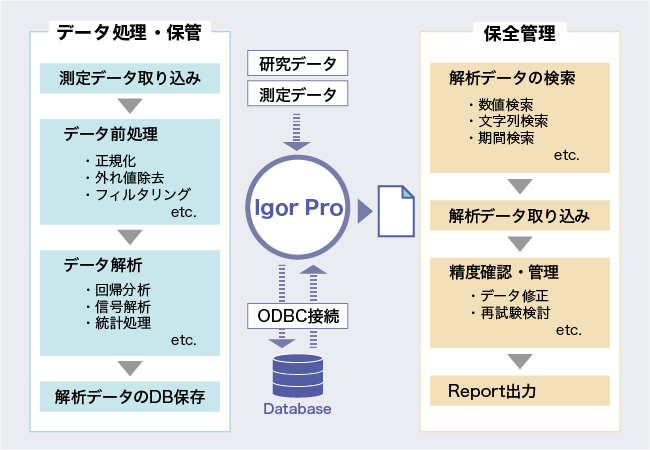
開発事例(2) 自動処理–データ取込から解析処理・出力まで–
【特徴】
- csv形式を始め、jsonなど多様なデータ形式に対応
- Igor Proのバックグラウンドタスク機能を使用することで安定かつ簡単に自動化実装が可能
- ローカルPCで処理したデータをサーバーに保存
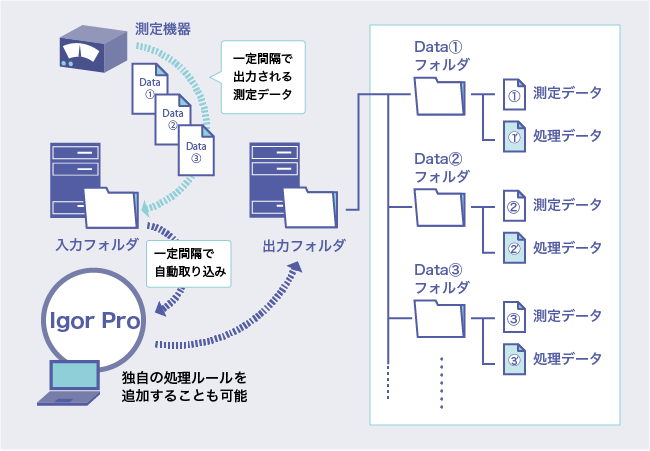
開発事例(3) モニタリングシステム–外部機器やシステムとの相互間のやり取り–
【特徴】
- CおよびC++を利用して、外部機器・システムとの連携が可能
- 測定機器・システムとデータとのやり取りが可能
- 異常値の検出ロジックなどの定義・実装が可能
- 解析に合わせたユーザーインターフェースの作成が可能
高い拡張性
独自の言語によって、ユーザーインターフェイスのカスタマイズや一連の動作の自動化が可能です。以下のオプションの拡張ツールを使えば、その機能をさらに拡張することが可能です。
- XOP Toolkit
C や C++ 言語を用いて Igor Pro の機能拡張(XOP)を開発するための SDK パッケージ - NIDAQ Tools MX
計測機器(National Instruments 社の DAQ デバイス)からダイレクトにデータを収集する機能を追加するパッケージ
開発元:WaveMetrics
機能一覧
ユーザーインターフェイス
Igor Pro は、高い性能ながら操作性の良いソフトウェアです。高度な機能を求めるユーザーのために用意されているプログラミング環境にもポイント&クリック機能が備わっており、上級者はもちろん初めて Igor Pro に触れるユーザーでも手軽に利用することができます。
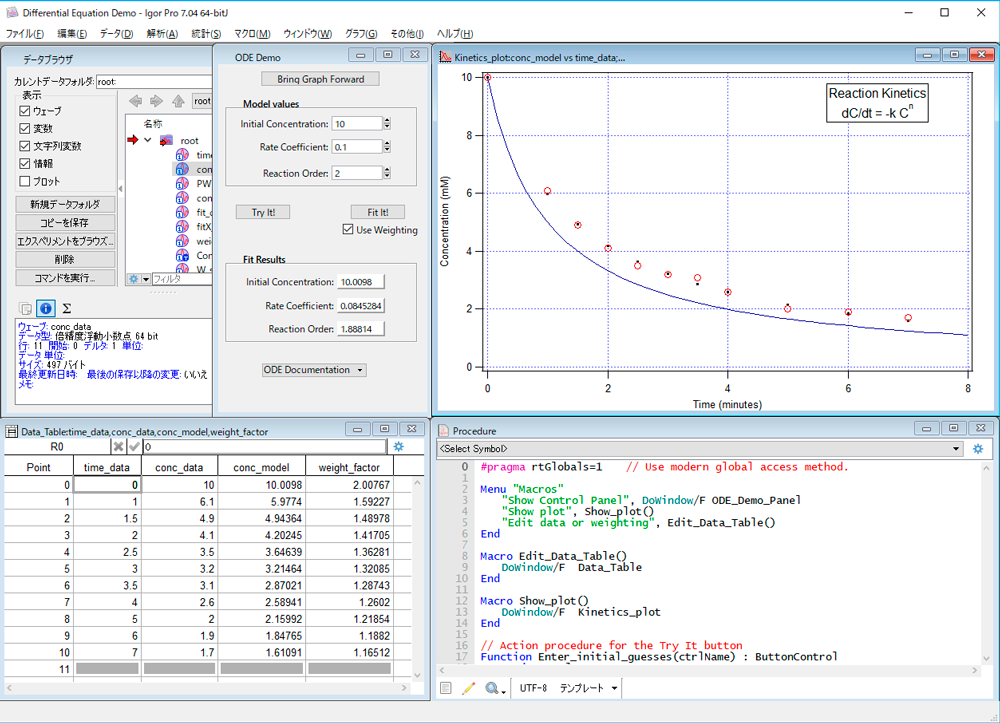
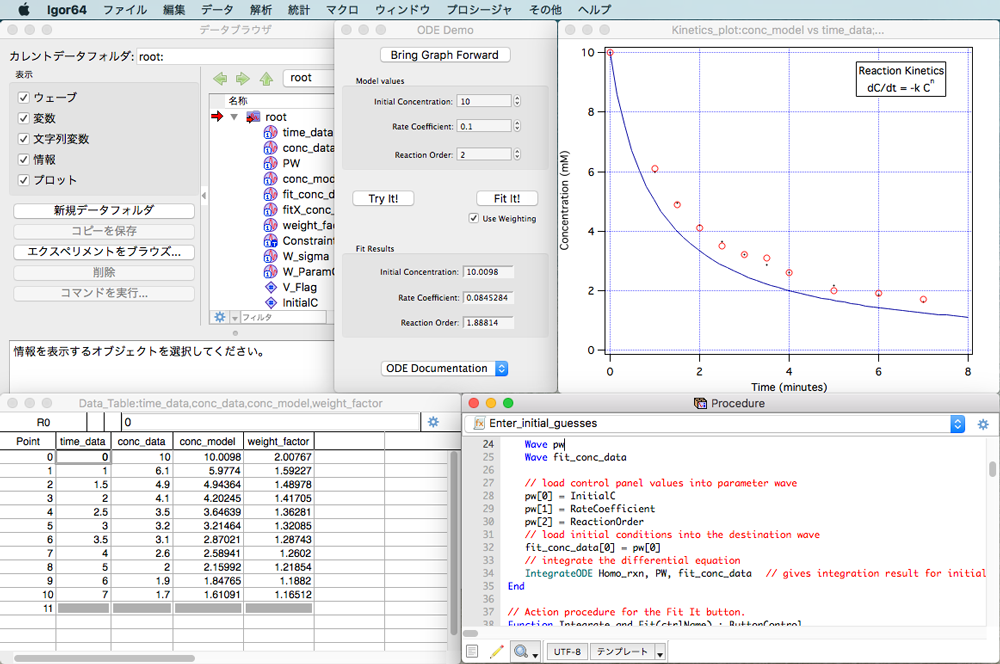
データの操作
テキスト、標準バイナリ、Excel、JCAMP、MatLab データなど、幅広い種類の形式のデータファイルをインポートすることができます。多くの画像ファイル形式の入出力にも対応しており、GPIB やシリアルポートなどのハードウェアデバイスからデータを読み込むことも可能です。任意の数のグラフやテーブルを任意の幅で複数同時に表示できます。文字列データ、内部 8 形式の数値データ、および4次元までのデータに対応しており、例えば100,000 ポイントを超える大規模なデータでも高速に処理します。
- データアクセス
- データインポート
- データの探索
- データの保存
充実したグラフ作成機能
Igor Pro の最も基本的な機能は、科学・技術向けグラフの作成です。作成するグラフのトレース、軸、等高線プロット、イメージ、注釈の数に制限はありません。グラフを他のグラフに埋め込んだり、複数のグラフやテーブル、注釈、画像を埋め込んだページレイアウトを作成することもできます。各曲線はそれぞれ独自の色、太さ、スタイルに設定でき、曲線上にある各ポイントの線の色、マーカーのサイズ、マーカーの形状 (またはテキスト) は、他のデータの値を利用することもできます。カテゴリープロットとエラーバーにも完全対応しています。グラフは簡単に拡大 (ズームイン) したり、移動 (パン) でき、各データポイントの座標値を返すカーソルがついています。
ページレイアウトウィンドウでは、グラフ、表、文字注釈および画像を扱えます。軸ラベルや注釈では、フォント、文字サイズおよびスタイルを組み合わせて使用できます。
パワフルなドローツールを用いると、ライン、矢印、長方形、ベジエ曲線、およびその他たくさんの図形で、グラフやページレイアウトに注釈を付けることができます。各描画オブジェクトの位置は、座標系で指定することができます。また、スクリーンまたはデータ座標を利用してグラフを呼び出したり、グラフをページレイアウトに追加することもできます。
注釈エディタでは、シンプルな下付き文字や上付き文字を正確かつフレキシブルにレイアウトできます。フォントやサイズの変更に自動的に応答し、動的にデータ値をインクルードするようにデザインされています。
また、Gizmo と Surface Plotter モジュールを使えば、驚くほど美しい 3Dグラフを作成することが可能です。ぜひ、ギャラリーページで “クール” なグラフィックスの数々をご覧ください。
- 2Dグラフ
- ページレイアウト
- テーブル
- ドローツール
- 注釈
- カラーテーブル
- サブウィンドウと埋め込み
- 3Dとボリューム
- グラフィックスのエックスポート
豊富なデータ解析機能
「データ解析」は、生のデータからその意味や重要性を引き出します。つまり、それが「どれだけ多いか?」、「どれくらいの高さか?」、「どのくらいの頻度か?」といった問いに回答を出します。
フーリエ、ウェーブレット、Hough 変換、無制限の独立変数を伴う組み込み関数又はユーザー定義関数への線形/非線形回帰曲線、微分、積分、常微分方程式、畳み込み 、ヒストグラム、スムージング、数学的表現による評価、多くの LAPACK ルーチンを利用した行列演算、信号測定、疎データ又は行列データの等高線化など、 幅広い分野での利用を想定した多彩な解析機能を実装しています。
- カーブフィッティング
- ピーク解析
- 信号処理
- 統計解析
- 関数の解析
画像処理機能
科学研究に利用される画像解析アプリケーションの全ての機能が備わっており、画像の取込から表示および処理のための理想的なツールです。 画像のフィルタリング、操作、粒子解析および、定量化のためのパワフルな画像処理操作関数が数多く搭載されています。
- 画像の取り込み
- ROI
- 画像変換
- カラースペースの変換
- 2値化
- Localized Filters
- エッジ検出
- 形態的操作
- 画像解析
プログラミング機能
Igor Pro にはすべての機能が体系化された強力なプログラミング言語が装備されています。これを使うことでデータのインポート、ファイルのインプット/アウトプット、データの取込、グラフ作成、図形の描画、印刷、その他ユーザーが求めるすべての操作を自動化できます。また、プログラムにはボタン、チェックボックス、ポップアップメニューといったメニュー機能や、パラメータをセットしたり結果を表示するためのコントロールを備えたコントロールパネルを作成することができます。問題あるコードを効率的に解決する構文 (シンタクス) の色分け機能とシンボリックデバッガでプログラミング作業を支援します。
- 180以上の組み込み関数と340以上の操作関数
- シンボリックデバッガ
- ユーザー定義可能な数学および文字列関数
- Igor Pro のすべての機能をプログラム可能
- 外部スクリプティングシステムによりコントロール可能
- プロシージャにおける構文の色づけ
- 統合されたヘルプとドキュメント
- 複数のプログラムソースを隔てた検索が可能
- カスタムインターフェイスの例
オプション製品
Igor XOP Toolkit は、C 言語プログラマーが Igor Pro の機能を拡張するためのパッケージです。 データ解析やデータ収集などのための操作関数、関数、メニュー、ダイアログおよびウィンドウを追加することができます。
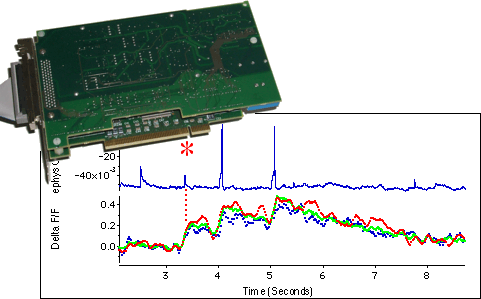
NIDAQ Tools MX は、Igor Pro にダイレクトにデータを収集させるための機能を追加するパッケージです。NIDAQ Tools は、National Instruments 社製の “multifunction data acquisition” ボードの多くをサポートしています。また、NI 社の NI-DAQmx ソフトウェアに対応するデータ収集デバイスの多くをサポートします。
古いバージョンの NIDAQ Tools コードやレガシーハードウェア(Windows 98 、OS 9 の Macintosh)との互換性のため、古いバージョンの NIDAQ Tools も提供されています。
多くのソフトウェア、ハードウェアメーカーが IGOR Pro 向けの、あるいは IGOR Pro と連携して使用できる製品を発売しています。詳しくはこちらをご参照ください。
アップデート情報
各アップデート情報は こちら をご確認ください
動作環境
Igor Pro 10 動作環境
Windows システム要件
IWindows 10 (ビルド 1809 以降) または Windows 11
64 bit アプリケーションのみ
Intel/AMD CPU 対応
macOS システム要件
Igor Pro 10 は、Windows 仮想環境下を除き、macOS では動作しません。
Igor Pro 10 は、macOS では動作しません (Windows 仮想環境下を除く)。
Igor Pro 10 を購入すると、macOS 対応の旧バージョンのライセンスキーをリクエストすることができます。
詳しくは営業部 (soft.sales@hulinks.co.jp) までお問い合わせください。
ライセンス
Igor Pro には、使用可能範囲が異なる 2 種類のライセンスがあります。いずれのライセンスにおいても機能的な違いはありません。
シングルユーザライセンス
シングルユーザライセンスは、1 ライセンスにつき 1 台のコンピュータにインストールして使用することができます。
ライセンス保有者個人が専属で使用する場合に限り、ライセンス保有者個人が所有する自宅のコンピュータやノート PC など、2 台目のコンピュータにインストールすることができますが、2 台同時に使用することは禁止されています。
マルチユーザライセンス
3 user 以上のグループ~サイトで、複数のユーザーが複数のマシンで Igor Pro を同時に使用することができます。
インストールする台数に制限はありませんが、同時に起動できるのは購入時に指定されたユーザー数までです。(Igor Pro の起動数の管理方法は、ユーザーに委ねられています。)
トライアル
デモ版お申込み
- デモ版は 30 日間製品版と同じ機能を使用することができます。30 日を過ぎますと、以下の点が制限されます。
- ファイルの保存ができなくなります。
- クリップボードにコピーした内容は他のアプリケーションにはペーストできなくなります。
- 印刷時に IGOR に関連した語句は重ねうちされ、結果的に製品版より印刷速度が遅くなります。
最新更新プログラム
WaveMetrics 社 Current Software Versions ページでダウンロードできます。
| Igor Pro の実行中に更新を確認するには、Igor の「ヘルプ」メニューから「Igor Pro の更新」を選択します。 Igor Pro は起動時に自動的に更新を確認できます。 自動更新チェックは、[その他設定]ダイアログの[更新]カテゴリで無効にできます。このダイアログではベータ版の確認も可能です。 |
製品価格
※ 価格、アップグレード価格、オプション製品についてはお見積りフォームからお問い合わせください。
| ライセンス | 製品 |
|---|---|
| 年間 | Igor Pro 年間 シングルユーザライセンス |
| Igor Pro 年間 シングルユーザライセンス 教育用 | |
| Igor Pro 年間 学生用 | |
| 無期限 | Igor Pro 10 シングルユーザライセンス |
| Igor Pro 10 シングルユーザライセンス 教育用 | |
| Igor Pro 10 マルチユーザライセンス (3 user 以上から) | |
| Igor Pro 10 マルチユーザライセンス 教育用 (3 user 以上から) | |
| アップグレード | Igor Pro 10 シングルユーザライセンス アップグレード |
| Igor Pro 10 シングルユーザライセンス 教育用 アップグレード | |
| Igor Pro 10 マルチユーザライセンス アップグレード | |
| Igor Pro 10 マルチユーザライセンス 教育用 アップグレード |
| ご購入の際は、ユーザー情報 (日本語・英語・e-mail アドレス) が必要です。 Igor Pro 10 は、Windows 仮想環境下を除き、macOS では動作しません。Igor Pro 10 を購入すると、旧バージョン (Mac 対応版など) のライセンスキーをリクエストすることができます。 オペレーティングシステムの言語が日本語の場合、Igor Pro 10 のインターフェイスの言語は自動的に日本語に切り替わります。英語にする場合は「その他の設定」ダイアログで変更できます。 |
教育用/学生用 価格について
以下に当てはまる方には、特別価格が適用されます。機能は、通常価格のものと変わりません。
- 教育用価格
教育機関、および、教育機関に所属し教育・研究目的で購入される方に適用される価格です。
ご購入の際は、ユーザー情報(日本語・英語・e-mail アドレス)が必要です。
| ※教育用価格が適用される機関 ・国公立および私立の幼稚園、小学校、中学校、高等学校、大学(短大含む)、大学院、高等専門学校、盲学校、ろう学校、看護学校、養護学校。また文部科学省以外の中央・地方官庁の管轄する大学校(防衛大学、水産大学校、海上保安大学校など)、短期大学校、学校(消防学校、職業訓練校、警察学校など)。 ・国立研究開発法人などの研究機関、文部省が設置した、研究所、博物館、天文台、大学共同利用機関等は一般用の扱いとなります。 |
- 学生用価格
学生が個人の資金で購入し、個人使用を目的とする場合に適用される価格です。
(研究室での使用や校費で購入の場合は、教育用価格が適用になります。)
(博士研究員は学生用ライセンスを購入する資格がありません。)
ご購入の際は、ユーザー情報(日本語・英語・e-mail アドレス)と「学生証のコピー」が必要です。
| ・学生用は年間ライセンスのみです。アップグレードはできません。購入後の払い戻しはできません。 ・学生用は個人向けライセンスとなりますので、譲渡はできません (ユーザー変更して第三者が使用することはできません)。 ・「学生個人が所有するコンピュータ 1 台」にインストールすることができますが、研究室や所属機関が所有するコンピュータへのインストールは固く禁じられています。 |
Igor Pro オプション製品
| ・オプション製品を購入するためには、Igor Pro(別売)が必要です。 ・オプション製品には、教育用価格・学生用価格はありません。 |
お見積り・ご購入
※ ご購入の際は、ユーザー情報 (日本語・英語・e-mail アドレス) が必要です。
※ アップグレードの価格・お見積りは 【現在お持ちの製品名、バージョン、シリアル又はライセンス番号】を必ずご記入ください。
サポート
サポート情報
- Igor Pro テクニカルサポート情報はこちら
- IgorExchange
Igor Pro ユーザーのフォーラム。簡単なコード(スニペット)からプロジェクトまで IGOR に関する幅広い情報を交換します。 - Igor Mailing List
Igor Pro のメーリングリスト。WaveMetrics の最新情報もここに配信されます。
Igor Pro 個別相談会
1989 年の製品誕生以来多くの研究者にご愛顧いただいている数値データ解析/可視化ソフトウェア Igor Pro。弊社では現在、Igor Pro の概要と基本的な操作セミナー「はじめての Igor Pro ~基本の「基」~」を定期的に開催しておりますが、この度は、お客様の個別の使用状況でのご不明な点やご不便な点についてお話を伺い、解決案を導き出す為の「個別相談会」を開催いたします。お気軽にお申し込みください。
| 例えば… ・「はじめての Igor Pro」を受講したが、実際にどの様に使用していけば良いか相談したい。 ・新しい業務でも Igor Proを活用したいが、グラフ化や解析方法で相談をしたい。 ・ユーザ定義の関数による回帰分析を行いたいが、うまくいかない。 ・プログラミングによる自動化・効率化が出来ないか。 …などなど |
| 形式: | 1 時間の個別相談 (Web) |
|---|---|
| 費用: | 無料 |
| 申込方法: | 本相談会は事前予約制となります。 相談したい内容を以下に送付ください。 soft.support@hulinks.co.jp 日程調整の上、ご返信させていただきます。 |

サポートお問い合わせ
導入事例
IGOR Pro ユーザー事例:

一つのエクスペリメントファイルの中でたくさんのウェーブを扱うことができるので,一連の実験を一つのエクスペリメントファイルで整理できることも便利です。(24/7/10)

このソフト一つで、複雑なデータ統計解析から魅力的な図の作成、大容量データ処理の他にも様々な魅力を兼ね備えています。コマンドウィンドウで解析過程を確認できるので同僚とデータを共有した時の確認等にも便利です。(23/10/12)
構造由来のユニークな物性にフォーカス、高圧環境下で測定されるデータ解析にIgor Proを使用

計測結果と仮説モデルとのフィッティングをほぼリアルタイムで比較表示できるIgorProは、常圧時とは前提や処理するデータ数が大きく異なる超高圧力下でも充分機能し、解析結果の確認もスムーズでとても助かっています。(20/12/18)
超低温域での核磁気共鳴 および 電子スピン共鳴(ミリ波領域) の測定と分析にIgorProを使用

はじめはwaveという考え方に戸惑いましたが、徐々に慣れました。多くのデータが一つのファイルにまとめられるので、PC内のファイルもスッキリです。(18/10/26)
力学物性マッピングによる材料評価にIgor Pro を使用 ナノメートルスケールでの力学物性の分布を直接に可視化

IgorProは「大量データを柔軟にさばける優れたグラフ表示ソフト」であるだけではなく、例えば、使いやすいマルチスレッド関連機能で簡単にマルチコアCPUの恩恵を得られるような、自由度が高くて開発効率に優れたプログラミングができます。(18/10/05)
カロテノイドの光合成における高効率なエネルギー移動とエネルギー変換効率の機構解明による人工光合成デバイス創成の試み

カロテノイドの機能を解明し、高効率なエネルギー移動と変換効率の要因をふまえることで、高効率な人工光合成デバイスの創生に大きく貢献 できると期待しています。(18/08/03)

シミュレーションでは、IGOR Pro に組み込まれているフーリエ変換、ヒストグラムや複素数演算等の充実した関数を利用して、伝送特性の詳細な評価・検証が可能です。(15/09/25)

測定して得られたデータはすべてIGOR Pro で扱っています。 高専の教員なので、研究だけでなく教育にも力を入れています。授業で扱うグラフの作成にも IGOR Pro を使用しています。(14/10/01)

データ整理、高度な解析、グラフ描画、プログラミングが 一体となっていて、ほとんどの場合他のソフトウェアを 使う必要がなく、非常に有効なツールです。(14/10/01)

特に高速フーリエ変換/逆フーリエ変換の機能が強力なので、IGOR マクロ言語を使えばコーディングが非常に楽になるということを実感しました。(12/12/28)

千年に一度といわれる自然災害により、野生動物がどのような影響を受けるのかを明らかにしていこうと考えています。今回の事例は IGOR Pro のユーザで東日本大震災で被災され、復興活動もされた東京大学の佐藤先生に特別編として話を伺いました。(12/07/06)

山本研究員は、衝突クレーター形成実験のデータ解析に IGOR Pro を利用されています。 研究室にご訪問させていただき、お話を伺いました。

MFP3D は、Asylum Research 社の開発した AMF (原子間力顕微鏡: Atomic Force Microscope) です。オフライン状態におけるデータの分析や操作はもちろん、リアルタイムで行う機器の制御およびデータ取り込みの基礎となる部分においても IGOR Pro が利用されています。
NeuroMatic は、電気生理学データの分析用に作成された IGOR Pro の関数がまとめられたパッケージです。
Nclamp パッケージは、電気生理学やフォトメトリー(光度測定)等さまざまな分野におけるデータ取り込みソフトウェアを提供します。
「応用物理学実験」の講座で利用(東京大学工学部)
「応用物理学実験」の講座ではコンピュータを使った大量のデータの収集・解析など の計測の手段として、 さらにはコンピュータを中心とした実験環境そのものの制御・管理などコンピュータ を利用した様々な研究 環境に触れ、研究遂行上必要となるコンピュータの利用法についてのイメージを与え、外部計測機器とPCを 接続した環境を実際に経験させさらにフーリエ変換の概念と利用法を教授されていま す。 この講座にIGOR Proが教材として導入されています。
原子力部門のデータの解析とグラフ化に利用(エンジニアリング開発株式会社 システム設計部)
IGORを原子力部門のデータの解析とグラフ化に使っていますが、非常に高性能で重宝しています。この領域では、いまだに開発言語としてFORTRANをメインで用いているため、エクセルとの連携がうまくとれません。特にデータ出力を行う場合、エクセルではバイナリデータが扱えないので、これまで非常に多くの時間と手間を掛けていました。その点、IGORは大量 のデータを高速に処理に、なおかつバイナリも含めて様々なデータを直接扱うことができるので非常に助かっています。グラフ描画に関しても、複数の線を同時に重ね合わせたり、拡大したりすることができるので分析の際には大いに役に立っています。
またIGORでプログラムを書けるようになるまでに多少時間がかかりましたが、マクロを覚えてしまったので、今まで一晩かかったような作業を数分で実行させることができるようになりました。実験を定型化して複数回処理するような作業ではマクロ機能の有無が大きな差につながると思います。このマクロとの連動は同系列のソフトである、Mathematicaやカレイダグラフ、DeltaGraphなどよりも優れており、ワードやエクセル、VBとの連携も非常に良くとれています。エクセルの代替ソフト以上の機能があり、エクセルと同じ使い方をしてもなおメリットがある点が評価できます。グラフの部分拡大や、データの抽出、注釈の追加など初心者にも嬉しい機能といえます。マニュアルの和訳もなかなか良いできだと思います。
改善してもらいたい点として、他のイラストレータなどのソフトとも連動して動くようになること。このソフトを使いこなせば、かなりの事ができるので、研究者であれば十分な使い勝手だと思います。大学の研究室やシンクタンク、またデータの解析を専門に行うような人、音の振動などを分析する人など十分に活用できるところは多いのではないでしょうか?
信号処理、大量時系列データの処理等に使用(大手電気メーカー 研究所)
グラフのきれいさと、Excelでは扱えないような大量データ(wave)などの扱いが可能なのが良い。 あと、処理が高速なところも良い。
模型実験や実船実験のデータのグラフ化。流体力学計算結果 のグラフ化。論文掲載用のグラフのほとんどに使用。(海洋科学技術センター 海洋技術研究部 田村 兼吉様)
完全に自分の思っている形のグラフが描ける。 データ量が多くても、テキスト形式でも 読み込みが可能なところが良い。
学術雑誌、学会発表用のグラフの作成に利用。(滋賀県立大学工学部 山下 義裕先生)
読み込めるデータ数が多く、図面の仕上がりがきれい。また、レイアウトがきれい。 グラフ上で簡単にデータをx軸やy軸方向にシフトできる。