FlexPDE の主な特徴
想像してみてください。偏微分方程式系を自由に入力し、取り扱う問題領域を併記するだけで、その内容を洗練された有限要素モデルへと容易に変換できるとしたら…。更に、以下の様々な機能を手軽に利用できるとしたら…。
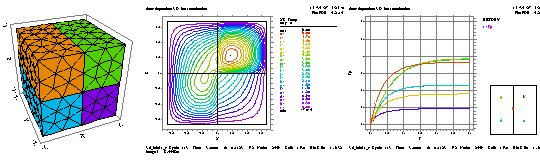
VisIt による FlexPDE データの可視化例
 |
- マルチスレッド機能*
- 自動メッシュ作成
- 任意の複雑さをもつ方程式の取り扱い
- 任意数の連立方程式の取り扱い
- 方程式の集合(セット)*
- 複素数、ベクトル、配列を用いた変数の取り扱い*
- 特定領域内における変数の無効化*
- 非線形方程式ソルバ
- 一次、二次、三次元空間の取り扱い
- 時間依存、定常状態、固有値
- タイムステップの動的制御
- 適応型メッシュの動的微調整
- ALE ( Arbitrary Lagrange/Eulerian ) 法を用いた動的メッシュ再構成手法
- 柔軟で統合的な画像出力
- Tecplot や VisIt 用のデータ出力による高品質な可視化**
夢を語るのはここまでです。FlexPDE を手にすれば、ここに列挙したすべてを叶えることができます。
スクリプトを記述する
 |
|
解析結果を可視化する
 |
|
世界最先端技術を研究する何百もの科学者たちと一緒になり、現在、最も汎用性の高いこの問題解決環境を活用しましょう。
FlexPDE は、他のパッケージの解析処理に必要とされる変換結果を単に渡すだけではありません。FlexPDE は、他のアプリケーションから処理を呼び出すパッケージとしても利用できるよう設計されています。
FlexPDE の機能
- 1次および 2次の偏微分方程式を 2次元、3次元座標で解けます。2次以上の高次についても扱えますが、この場合は、中間変数を用いて、高次微分または偏微分を表現します。
- 定常状態、時間依存、その混合のいずれも扱えます。また、固有値問題も扱えます。
- 任意数の連立方程式を扱えますが (連成問題)、その規模は、走行するマシーン能力に依存します。
- 線形、非線形の両方を扱えます。非線形システムは修正ニュートン・ラフソン法で解いています。
- 異なる物体につき、任意数の領域を定義できます。定義する変数は、物体上で連続とします。微分のジャンプ条件は、偏微分方程式システムの記述で指定できます。
豊富なサンプル例題
- 配布される FlexPDE には標準で 100 以上の例題が含まれています。それらは FlexPDE の多くの学問領域への応用を示したものです。これらの例題の記述文は、標準的なインストール手順でインストールされ、そのディレクトリの「Samples」フォルダにツリー構造で存在します。こうした既存の問題記述文のコピーに変更を加えることが、新しい問題の記述文を作り始めるのに最も効率的な方法です。
- また、配布される FlexPDE の "Backstrom_Books" フォルダにも多くの例題が Gunnar Backstrom 教授の書かれた本から引用されています。その本はアカデミック環境での FlexPDE の利用を示したものです。
資料: