 |
| サイトマップ | |
|
 |
| サイトマップ | |
|
有限要素解析による物理学における場
|
| TITLE {exa021.pde } 'sin(x)*x*cos(x) ' DEFINITIONS Lx=10 Ly=1 {Define extent of (x,y) space } f=sin(x)+x*cos(x) {Function to be plotted } fx=dx(f) {First derivative } fxx=dxx(f) {Second dervative } BOUNDARIES region 'domain' {Region for function } start(-Lx,-Ly) {Draw boundary counter-clockwise } line to (Lx,-Ly) to (Lx,Ly) to (-Lx,Ly) to finish PLOTS elevation(f,fx,fxx) from (-Lx,0) to (Lx,0) END |
title などの文字ストリングは引用符で囲まなくてはならないことに注意してください。{} の中にはコメントが書け、各ラインの目的をメモるのに使えます。また、コメントは FlexPDE の処理対象にはなりません。例えば、第1ライン目に記述ファイルの名前を書いておくと便利です。
本書では、記述ファイル名の数字の最初の桁は章番号を示します。
definitions で使用される数学的記法は、他のプログラミング言語に似ています。* は乗算、^ は「べき」を意味します。FlexPDE では大文字、小文字の区別がなく、f と F は同じ変数になります。
sin(x) などの標準関数も用意されています。更に、偏微分も演算子として用意されています。
∂f/∂x は dx(f) と書けます。高次微分は dx(dx(f)) あるいは dxx(f) 等と書けます。
ここでの関数は、1変数だけですが、(x,y) 空間に領域 (region) を確保する必要があります。これを 20 * 2 とします。boundaries 部では、この領域の形状とサイズを (x,y) 座標で定義し、間を直線で結びます。領域内部が常に左側に来るよう、領域の境界は正方向 (反時計周り) に定義します。
最後に elevation プロットの指定を行っています。これは、曲線を描きます。同一図にいくつかの関数をプロットすることができますが、これが有効なのは、関数値がお互い比較可能な大きさである場合に限られます。関数 f(x,y) の elevation プロットは (x,y) 平面上の線を出力します。これを from...to 文で指定しています。このタイプのプロットは、所与の線上の関数表面の高さを示します。
記述ファイルを読みやすくするため、アイデントを入れたり、自分の好みに合わせてページを設計するのがよいと思います。
エディタ上部の Run をクリックするとプログラムの実行が始まり、下図が直ちに出てきます。
3つの曲線 a, b, c は色で区分され、それは右の表に示されています。表の下にある小さい図は (x,y) 平面上で選択した基準線を示します。曲線は、ゼロ線に対する最小、最大を示しています。
別の関数を上記と同じ方法で調べることもできます。式が上記記述ファイルのものより、更に複雑な場合には、項をグループ化し、必要であれば、2ラインに分けて書くこともできます。FlexPDE は各部分の解析を行うので、継続行である指定はいりません。また、項の間に余分なスペースを入れて読みやすくしても構いません。definitions 部に示すように、1ラインに2つ以上の代入文を書くことができます。分離マークは不要です。
exa021での実験が終了したら、File, Close をクリックして画面をクリアし、次にトライできます。
次に 2変数関数を調べましょう。これが実は、FlexPDE が設計されたきっかけでもあります。新たに記述ファイルを作る場合、2つの方法があります。File, New をクリックして入力するか、既存のファイル (exa021) を Open し、SaveAs をクリックして別名のコピーを作り、これを修正します。今回の内容が、既存ファイルに類似している場合、後者が望ましいことはいうまでもありません。
| TITLE {exa022.pde} ' x^2+2*y^2' SELECT spectral_colors {Values from red to violet} DEFINITIONS Lx=1 Ly=1 f=x^2+2*y^2 grad_f=vector(dx(f),dy(f)) laplace_f=dxx(f)+dyy(f) BOUNDARIES region 'domain' start(-Lx,-Ly) line to (Lx,-Ly) to (Lx,Ly) to (-Lx,Ly) to finish PLOTS grid(x,y) {Triangular mesh} surface(f) {Surface in 3 dimensions} contour(f) {Contour plot of function} contour(f) painted {Color coded in plane} vector(grad_f) as 'Gradient' {Arrow plot with a title} contour(laplace_f) {Test if f(x) is harmonic} END |
このファイルを走行させると、画面上に全てのプロットの縮小バージョンが表示されます。
いずれかの図の内部をダブルクリックすると、図が拡大されます。ここで再度ダブルクリックすると、もとの縮小バージョンに戻ります。
拡大された状態で、右クリックし、Print を選択すると、用紙にプリントできます。PrtScr (print screen) キーを使って図をワープロに貼り付けることもできます。
上記ファイルの最終部分は、grid のプロット(下図)から始まっています。この図は、領域のセルへの分割状況を示しています。FlexPDE は三角形セルの各頂点および各辺の中点での関数値を計算します。これらは参照値であり、これらの中間値や微分を求めるには、多項式 P(x, y) を当てはめて内挿します。通常、grid プロットを行う必要はありません。自動的にステータス・ウインドゥに自動的に示されるからです。
このファイルが出力する2番目の図 (下図) は、関数値を (x,y) 平面上での高さで表現した surface プロットです。色表示もしていますが、低い値を赤、大きな値を紫とする、光の周波数 (エネルギー) 順となっています。これは温度の場合にも適用できます。つまり、金属ははじめ赤から始まり、熱すると白みがかってきます。select で spectral_color を指定しているのは、デフォルトはその逆順であるからです。
曲面上のたとえば、2.00 と 2,10 の間の値をとる全ての点は、同じ色になっています。つまり、2つの色の間の境界線は、プロットの右側のテーブルから読み取れる f(x,y) の値に対応しています。
surface 図は、座標軸に関しある一定角度からみたものですが、図上で右クリックし、Rotate を選択して、「カメラ」を移動させることができます。右の表の上部にある3つの値、カメラ座標 (x,y) および仰角 (度) が視点の現位置を示します。
3番目の図は contour プロット (下図) で、(x,y) 平面上の一群の曲線で構成されています。各曲線はfの一定値に対応しています。これらの関数値は、隣接の表から読み取ることができますし、領域上での最小、最大値も示されています。この図は、surface プロットを上から見たもので、異なる色の間の境界線が等高線になっています。
painted の contour プロット(下図)は、等高線間の空間を色で塗りつぶしたものにすぎません。また、上から見た surface プロットとみなすこともできます。色コードをみれば、関数が表現する表面をすばやく読み取ることができます。
definitions に現れる新しい機能は vector grad_f で、以下のように定義されます。
![]()
ここで、i と j は、x および y 軸に沿う単位長のベクトルです。このベクトルは、成分 dx(f) と dy(f) を使って簡単に表現できます。その結果、勾配場を矢印で表現できます。各矢印は、最大勾配の方向および、大きさ (長さで表現) を示しています。色によっても表示されています。
この場合、全ての矢印は中心から遠ざかる方向にあり、このことは、最小値が原点 (0, 0) にあることを示しています。
最後の図は、∇ 演算子を 2回作用させて得た laplace_f を示しています。
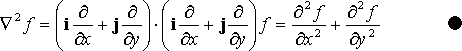
これに対応する contour プロット (ここには示しませんが) には、曲線が全くなく、最大、最小値がほぼ等しく 6.0 に近い値で、小数点第4桁で異なるだけです。これは関数 laplace_f が定数であることを示しています。∇2(f) がゼロでなければ、f(x) は調和関数1p477ではない、ということになります。
これまでに New あるいは SaveAs を使って2つの記述ファイルを作ってきました。既存ファイルを見たり、修正したい場合には、Open を選択して、ファイルを特定できます。
このような方法でもいいのですが、エクスプロアラから FlexPDE を管理する方がもっと便利です。
記述ファイル・フォルダに含まれているファイルはウインドゥの右側に示されていることが解ります。1ラインあたり 1ファイルのリストを得るには、デフォルト・レイアウトで View, Details を選択しておけばいいのです。また、View, FolderOptions, Classic style をクリックし、View の下で Display the full path in title bar を選択しても構いません。
FlexPDE が走行していなくても、ファイルのアイコンをダブルクリックすれば、例えば、exa021 のエディットを行えます。次に exa022 を開始すると、FlexPDE を 2度コールしたことになり、画面下部に各ファイルのボタンが示されます。このため、ファイル間のスイッチが容易になり、特にファイル間でまとまったラインをコピーしたいときに便利です。また、2つの実行結果を比較するときにも便利です。
2つの pde ファイルの他に、始めの名前が同じである2つのグラフイック・ファイル (pg3) があり、色のついたアイコンが表示されています。このようなファイルには得られたプロットが格納されており、アイコンをダブルクリックすると見ることができます。
また、拡張子が log のファイルがありますが、ここには実行に関する情報が格納されています。
これらのファイル・アイコンをダブルクリックしますと、オープン方法を聞いてきます。たとえば全てのウインドゥ・システムに入っている Notepad などを選択します。log ファイルにはそのまま読める文字が入っていますが、そのメッセージを解読する必要は殆どありません。
新規にプログラムを実行するつど、グラフイックスおよび log ファイルが作られ、ファイル数が非常に多くなってきた場合には削除する必要があります。グラフイックス・ファイルは大きくディスクを沢山使用します。
ファイル・ウインドゥ上部に Name, Size, Type, Modified のボタンがあります。これらはフォルダ内容を管理する上で便利です。Name をクリックしますと、ファイル名がアルファベット順に配置されますし、もう一度クリックしますと逆順になります。Size を使用すると即座にどのファイルが大きいか解ります。Type, Modified を使用しますと、リストを便利な形で見ることができ、ファイルの削除を行う場合特に役立ちます。
FlexPDE には Help ボタンがあり、各種コマンドのシンタクスなどの情報を提供してくれます。馴染みのないコマンドに出会ったら、Help を参照してください。印刷されたマニュアルも付属しています。
Lx, Ly の値を変えながら、下記関数を調べてみましょう。
これまでに任意関数のさまざまな側面を示してきました。次に、流体力学で現れる全ての点において速度ベクトルが定義されるようなより現実的な場を見ていくことにします。まず、軸の回りに流体が回転する幾つかの簡単な場合を考察します。この場合、各点における速度 v は半径ベクトルに垂直であり、その大きさは |v|=ωr となります。これらは、下記の行列式でまとめて表現できます。
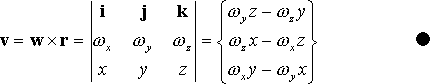
FlexPDE は 2D という限界があるので、(x, y) 平面に限定され、従って上式 3行目の vz はゼロとおくことになります。従って、ωx=ωy=0 が要求され、z 成分のみ残ることになり、これを単に ω とします。
この場合、ω は全領域上で同一になります。ここで示す記述ファイルは、この運動のさまざまな特徴を調べるのを目的としています。円形領域を定義するために、新しいコマンド arc を使用します。これによって 1/4 の円を連続して描けます。definitions 部では特別な微分演算子
div(v) および (∇×v)z を導入しています。後者は、curl(v) の z 成分です。(x, y) 座標でのこれら演算子は以下のように定義されます。
![]()
ここでは、3番目の成分 (z) のみを使用します。
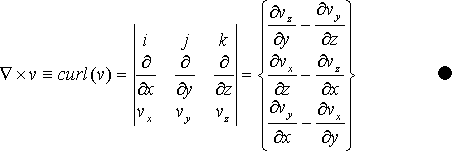
| TITLE {exa031.pde} ' Liquid Rotating as a Disk' SELECT spectral_colors DEFINITIONS {SI units} r1=1.0 rad=sqrt(x^2+y^2) {Radius=square root} omega=1.0 {Angular velocity} vx=-omega*y vy=omega*x {Velocity components} v=vector(vx, vy) {Velocity vector} vm=sqrt(vx^2+vy^2) {Magnitude of v} div_v=dx(vx)+dy(vy) curl_z=dx(vy)-dy(vx) BOUNDARIES region 'domain' start(r1,0) arc to (0,r1) to (-r1,0) to (0,-r1) to finish {Circular arc} PLOTS contour(vx) contour(vy) contour(vm) contour(div_v) contour(curl_z) vector(v) END |
上図は、速度ベクトルのプロットです。発散 div_v は一定で、値がゼロになっています。curl_z もほぼ一定で 2.000 であるため、等高線プロットには何も現れません。これら関数は容易に計算できますし、手計算でも簡単にできますが、FlexPDE ではも更に複雑なベクトル場についても同様のプロットを簡単に行えます。
次に角速度 ω が半径 R につれて変化するような場合を調べてみましょう。このような変化は流体に存在しますが、ここでその詳しい議論はしません。以下の記述ファイルは exa031 をもとに修正したもので、ω=1/R2 としています。
| TITLE {exa032.pde} ' Non-Constant Omega' SELECT spectral_colors DEFINITIONS {SI units} r1=1.0 rad=sqrt(x^2+y^2) omega=1/rad^2 {rad=R} vx=-omega*y vy=omega*x {Velocity} v=vector(vx, vy) vm=sqrt(vx^2+vy^2) {Magnitude} div_v=dx(vx)+dy(vy) curl_z=dx(vy)-dy(vx) BOUNDARIES region 'domain' start(r1,0) arc to (0,r1) to (-r1,0) to (0,-r1) to finish PLOTS contour(vx) contour(vy) contour(abs(vx)) log {Log10 of absolute value} contour(abs(vy)) log contour(div_v) contour(curl_z) contour(vm) log vector(v/vm) {Unit magnitude} END |
殆どの変化は原点近傍で発生しているため、vx と vy の等高線図にはあまり意味がないのは明らかです。
関数値の変化を広い範囲で見るために、修飾子 log を指定して、10 の対数で等高線図のプロットを行っています。vx と vy の大きさの対数プロットは、90 度回転している点を除けば、似通っています。
curl_z のプロットはちょっと変わっています。これは多くの不規則な形状のゼロ等高線で構成されています。表にある他の等高線の値は 10-10 のオーダーになっています。これは exa031 では 2.0 であったものです。数値計算につきものの丸め誤差については、curl_z の値は全領域にわたってゼロになっています。このことは正確な計算によっても容易に確かめることができます。発散 div_v もゼロになっています。
vm の等高線図および正規化したベクトル図 (v/vm) で、各点での速度および方向がわかります。従って、これらのグラフはベクトル場を完全に表現しているといえます。
次に、ω=sin(R) の場合を見てみましょう。exa032 を次のように少し修正すればいいだけです。
| TITLE {exa032a.pde} ' Non-Constant Omega' .......... r1=1.0 rad=sqrt(x^2+y^2) omega=sin(rad) .......... |
この記述ファイルを実行すると、流体は前例と全く同じように回転していますが、curl_z は明らかにゼロではないことがわかります。しかし、発散 div_v の値はほぼゼロになっています。
どのような回転運動が curl_z の非ゼロ値をもたらすのでしょうか? ベクトル解析には以下の定義があります。
![]()
ここで線積分は、(x, y) 平面の領域 S の閉曲線 C に沿って行うものとします。この状況を下図に示します。無視しうる大きさに縮小する領域部分を灰色で示しています。この部分は2つの半径方向部分と2つの回転方向部分で区切られています。ベクトル v は回転方向経路に沿っており、半径方向部分は積分に全く寄与しません。回転方向部分からの寄与は速度 vm に弧長を乗じたものだけで、これら2つの項の符号は逆になっているため、互いに相殺されてしまうこともあります。
exa031 では、外側経路はもっと長く、更に速度ももっと大きくなっていました。これらの強めあう要素は半径に比例するため、その結果、curl_x の値は非ゼロになります。
ω = 1/R2 の場合には、外側経路の速度はより小さくこれが経路長の増加を打ち消し、curl_z がゼロになったわけです。つまり、curl はたまたまゼロになったということです。
次の記述ファイルは、exa031を修正したものですが、まず、曲線 ’inner’ のプロットを行っています。これは円で偏心しています (r0 のため)。この曲線は finish で終わらないため、feature で定義します。見やすくするため、コマンド angle を使用して第2 の円も描きます。
| TITLE {exa031a.pde} ' Liquid Rotating as a Disk' SELECT spectral_colors DEFINITIONS {SI units} r1=1.0 r2=0.3 r0=0.2 rad=sqrt(x^2+y^2) {Radius=square root} omega=1.0 {Angular velocity} vx=-omega*y vy=omega*x {Velocity components} v=vector(vx, vy) {Velocity vector} vm=sqrt(vx^2+vy^2) {Magnitude of v} div_v=dx(vx)+dy(vy) curl_z=dx(vy)-dy(vx) BOUNDARIES region 'domain' start(r1,0) arc to (0,r1) to (-r1,0) to (0,-r1) to finish {Circular arc} feature start 'inner' (r0+r2,0) arc(center=r0,0) angle=360 PLOTS elevation(tangential(v)/(pi*r2^2)) on 'inner' {-> Curl_z} contour(vm/(pi*r1^2)) {-> Average} END |
これによって curl_z の推定を線積分で行えます。このため、v•dl≡vtdl の積分を閉曲線に沿って行う必要があります。vt は閉曲線に接する v の成分です。コマンド tangential は速度成分 vt を選択してくれます。関数の積分は自動的に行われ、小さい円の領域 S として分離しています。積分の計算結果は、下図の一番下のラインに示されています。
(∇×v)z の線積分は、r2 がゼロになるまで行うべきですが、ここに示す簡単な例題ではその必要はありません。曲線の半径を例えば、10 の倍数分ずつ減少させると、三角形がほとんどなくなって、精度の保証ができなくなります。
vm の等高線図では、(x, y) 平面上での積分が自動的に実行されています。これを、領域の面積で除すと、平均値が得られます。
いままでの例題では、速度場の発散はゼロでした。その理由を理解するために、次の積分の定義を考えてみましょう。
![]()
ここで、積分は前ページの図に示すように体積要素 V の表面 S 上で行うものとします。v はこれら表面の法線 n に直角であるため、箱の円筒表面は積分には寄与しません。2つの平面は (x, y) 平面に並行であり、速度は (x, y) 平面内に閉じ込められているため、これら平面上での積分もなんら寄与しません。半径方向の平面に関しては、速度は、半径 R に依存するため、等しく貢献しますが、反対の符号をとります。従って、ω が R のみに依存する場合、発散は必ずゼロになります。
前例では、軸の周りの回転を取り上げ、角速度は半径のみに依存するものとしました。これは流体の一般的な運動の特殊な場合にすぎません。次に、速度成分が R の独立関数であるようなもっと一般的な場について考えましょう。exa032 に以下の定義を加えてみましょう。
| TITLE {exa033.pde} ' More General Velocity Field' SELECT spectral_colors DEFINITIONS {SI units} r1=1.0 rad=sqrt(x^2+y^2) omega=1/rad^2 {rad=R} vx=-rad*tan(rad) vy=exp(rad) {Velocity} ............ |
発散の等高線図は、下図に示すように非ゼロとなります。curl_z も同様です。
しかしながら、速度のベクトル図には回転運動の形跡がなく、curl_z が本当に非ゼロになるのか疑わしく感じます。
本章の例題から得られる教訓は、ベクトル図が示すベクトル場は、curl または div がゼロであるかどうかの判定には十分ではない、ということです。これを明確にするには、微分あるいは積分の定義を適用する必要があります。