
マルチフィジックスの有限要素モデルを偏微分方程式で無制限に記述できる先駆的な問題解決環境
FlexPDE は、熱流動、応力解析、流体力学、化学反応、電磁気学、拡散など様々な物理現象を複合的にモデル化して PDE 問題として取り扱うことができます。数理モデルの構築から数値解法、グラフ表示までをこのソフトウェアツールひとつで実現できます。
応力解析から化学反応速度、更には、ストック・オプションの価格決定に至るまで、実世界を構成する数理モデルは、偏微分方程式によって支配されます。FlexPDE は、各分野に特化した専用アプリケーションではなく、方程式を処理することによって様々な領域にまたがる数学的基礎を取り扱います。この製品がひとつあれば、あらゆる数理モデル問題を解くことができるため、取り扱う問題毎にソフトウェア製品を幾つも買い揃える必要はありません。
FlexPDE の処理システムには以下の機能が装備されています。
- 記述された問題を解析し、
- ガレルキン有限要素法による積分、微分、および、従属関係をシンボルで形成し、
- マトリクスを連成したら、その解を求め、
- 結果をプロットに出力します。
以上のジョブを実行するのに他のソフトウェアを追加する必要はありません。新たな研究分野に取り組みたい場合も「追加モジュール」を購入する必要はありません。
機能一覧
製品概要
想像してみてください。偏微分方程式系を自由に入力し、取り扱う問題領域を併記するだけで、その内容を洗練された有限要素モデルへと容易に変換できるとしたら…。更に、以下の様々な機能を手軽に利用できるとしたら…。
- マルチスレッド機能*
- 自動メッシュ作成
- 任意の複雑さをもつ方程式の取り扱い
- 任意数の連立方程式の取り扱い
- 方程式の集合(セット)*
- 複素数、ベクトル、配列を用いた変数の取り扱い*
- 特定領域内における変数の無効化*
- 非線形方程式ソルバ
- 一次、二次、三次元空間の取り扱い
- 時間依存、定常状態、固有値
- タイムステップの動的制御
- 適応型メッシュの動的微調整
- ALE ( Arbitrary Lagrange/Eulerian ) 法を用いた動的メッシュ再構成手法
- 柔軟で統合的な画像出力
- Tecplot や VisIt 用のデータ出力による高品質な可視化**
*バージョン6の新機能
**(関連製品:SlicerDicer、MayaVi、AcuMesh)

夢を語るのはここまでです。FlexPDE を手にすれば、ここに列挙したすべてを叶えることができます。
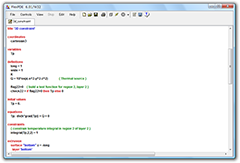
スクリプトを記述する
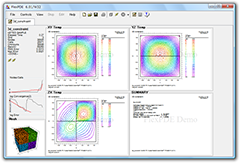
解析結果を可視化する
世界最先端技術を研究する何百もの科学者たちと一緒になり、現在、最も汎用性の高いこの問題解決環境を活用しましょう。
FlexPDE は、他のパッケージの解析処理に必要とされる変換結果を単に渡すだけではありません。FlexPDE は、他のアプリケーションから処理を呼び出すパッケージとしても利用できるよう設計されています。
FlexPDE の機能
- 1次および 2次の偏微分方程式を 2次元、3次元座標で解けます。2次以上の高次についても扱えますが、この場合は、中間変数を用いて、高次微分または偏微分を表現します。
- 定常状態、時間依存、その混合のいずれも扱えます。また、固有値問題も扱えます。
- 任意数の連立方程式を扱えますが (連成問題)、その規模は、走行するマシーン能力に依存します。
- 線形、非線形の両方を扱えます。非線形システムは修正ニュートン・ラフソン法で解いています。
- 異なる物体につき、任意数の領域を定義できます。定義する変数は、物体上で連続とします。微分のジャンプ条件は、偏微分方程式システムの記述で指定できます。
豊富なサンプル例題
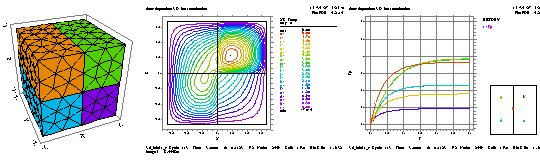
- 配布される FlexPDE には標準で 100 以上の例題が含まれています。それらは FlexPDE の多くの学問領域への応用を示したものです。これらの例題の記述文は、標準的なインストール手順でインストールされ、そのディレクトリの「Samples」フォルダにツリー構造で存在します。こうした既存の問題記述文のコピーに変更を加えることが、新しい問題の記述文を作り始めるのに最も効率的な方法です。
- また、配布される FlexPDE の “Backstrom_Books” フォルダにも多くの例題が Gunnar Backstrom 教授の書かれた本から引用されています。その本はアカデミック環境での FlexPDE の利用を示したものです。
FlexPDE とは?
FlexPDE とは何ですか?
- FlexPDE は、「記述式の有限要素モデル構築と数値解法」のソフトウェアです。
- ユーザーの記述によって、その記述文から偏微分方程式システムを有限要素でモデル化し、そのシステムを解き、そして、その結果をグラフィックや表出力する等の動作を FlexPDE が実行します。
- FlexPDE は、「問題を解く環境」も持っています。
- これは、偏微分方程式システムを解くのに必要な関数、記述文のためのエディター、有限要素メッシュを作成するメッシュ生成、解を求める有限要素解法、そして、結果をプロットするグラフィックシステムの全領域にわたる作業を実行する環境です。
- ユーザーは記述文を編集し、その問題を実行し、その出力を見て、それから修正し、そして繰り返し再実行することができます。しかも、こららすべてが FlexPDE の使用環境を離れることなくできます。
- FlexPDE は、あらかじめ定義された問題領域や方程式のリストを持っている訳ではありません。
- 偏微分方程式の選択はすべてユーザーの自由です。
- FlexPDE の記述言語は「自然」言語です。
- まるでユーザーが仲間に記述して説明するような方法に似た形式で、ユーザーが自分の偏微分方程式システムを数学的に表現し、自分の問題領域の図形を記述できます。
- 例えば、記述文には EQUATIONS 区分があります。そこにラプラスの方程式を記述しようとすると次のようになります:
| Div(grad(u)) = 0 |
-
- 同様にして、その記述文の BOUNDARIES 区分には、2次元の問題領域の幾何学的境界を単にその周囲をあるくように表現します:
| Start(x1,y1) line to (x2,y1) to (x2,y2) to (x1,y2) to finish |
- この記述形式には多くの利点があります。
- この記述文は方程式システムと問題領域を完璧に表現しますので、あたかも固定したアプリケーション・プログラムの場合のように、どんな方程式が解かれているのかの不確実性がありません。
- 新しい変数、新しい方程式、または新しい条件等は任意に追加できますから、違った物理的効果や異なった損失項は表すことが出来ない場合があるといったようなソフトウェアでは決してありません。
- 多くの異なった問題が同じソフトウェアで解くことができますので、問題毎に新しく学ぶというような難題もありません。
- また、このような記述モデルで必然的な影響もあります。
- ユーザーは自分の問題を数学的な形に表すことができなくてはなりません。
- 教育的な環境では、このことは良いことです。それが将に学生が学びたいことなのです。
- 産業的な環境では、特異な知識を持ったユーザーが記述文を作成し、それをもっと技術の未熟な職員が使いまた修正することもできます。そして、こうした応用問題の記述文の集積はそれがどのように為されたかを示すことができます。
どんな人が FlexPDE を使うのですか?
物理学や工学等の多くの問題は様々なレベルで偏微分方程式によって記述されます。このことは、FlexPDE のような記述型解決ソフトウェアが実質的に工学や科学のどの分野にも適用できることを意味します。
- 研究者は多くの分野で FlexPDE を使うことができ、それでもって彼らの実験や機器をモデル化し、予測し、いろいろな効果の重要さを調べることができます。パラメータの種類やその依存性が形式等によって制限されることはありませんし、任意にプログラムすることができます。
- エンジニアは、FlexPDE を用いて設計の最適化研究をし、また、実現性の調査、あるいは概念的解析をするために使用できます。この同じソフトウェアでひとつの設計のあらゆる面をモデル化するのに使用できます。各面での効果を調べる毎に別のツールを必要とはしません。
- アプリケーション・ソフトウェア開発者は、偏微分方程式システムの有限要素モデルを必要とする特定の目的をもつアプリケーション・ソフトウェアのコアとして FlexPDE を使用できます。
- 教育者は、物理学や工学を教えるのに FlexPDE を使うことができます。学問のあらゆる範囲の興味あるシステムを調べるのに、このたったひとつのソフトウェアツールで可能となります。
- 学生は、実際の方程式を見て、領域や条件を変更する毎に変化する結果とやり取りしながら実験ができます。
機能紹介
FlexPDE には何ができるのですか?
FlexPDE は、直交(デカルト)座標系あるいは 2次元軸対称座標系または 3次元直交座標系で、1階または 2階の偏微分方程式システムを解くことができます。
- このシステムは、定常問題でも時間依存問題でもかまいません。あるいは、代わって FlexPDE は固有値問題を解くこともできます。定常状態と時間依存方程式の混在した問題も可能です。
- FlexPDE を実行する計算機の限度にもよりますが、いくつもの連立方程式を解くことができます。
- 方程式は線形でも非線形でもかまいません。非線形システムは変形ニュートン-ラフソン反復法で解かれます。
- どんな数の異なった物質特性の領域も定義できます。
- モデル化される変数は物質の境界を通して連続であると仮定されます。微分に関する不連続(Jump)条件は、その PDE システムの記述文に依存します。
- FlexPDE は極めて使い易く、この特長から教育で使用することが勧められます。しかし、FlexPDE は玩具ではありません。その力を充分に使うことによって、極めて難しい問題でも成功裏に適用することができます。
どのような機能が装備されていますか?
FlexPDE は充分に統合された PDE 解決ソフトウェアで、完全な問題解決システムにいくつかのモジュールを組合せたものです。
- 記述文編集モジュールは、予約語の構文を強調表示し、完全なテキスト編集機能とグラフィック領域の表示機能を持っています。
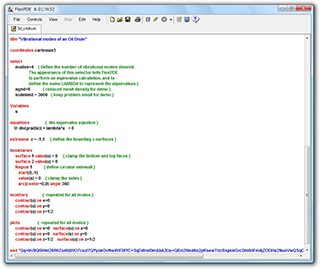
- 記号方程式解析モジュールは、定義されたパラメータとそれらの関連を展開し、空間差分を行い、記号的に部分積分を適用して 2階微分項を無くし、記号的にガラーキン方程式を作成します。次に、こららの方程式を差分化し、ヤコビアン結合行列を作成します。
- メッシュ生成モジュールは、三角形あるいは四面体の有限要素メッシュを2次元あるいは 3次元の問題領域にわたって構築します。2次元では、任意の領域を非構造化三角メッシュで覆います。3次元問題では、任意の 2次元領域が第3 の次元に伸長され、任意の分割面によって区切られます。その結果の 3次元図形は非構造化四面体メッシュで満たされます。

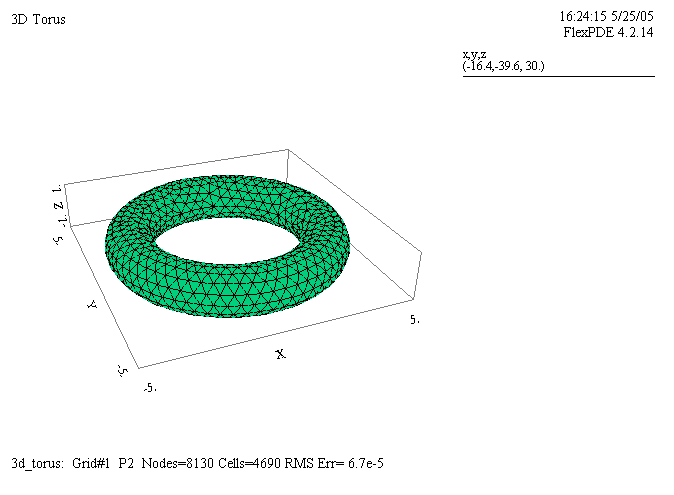
- 有限要素数値解析モジュールは、定常、時間依存あるいは固有値の問題の中から、別に用意された線形または非線形システムの手続きとともに、適当な解決体系を選択します。有限要素基礎関数は 2次か 3次のどちらかです。
- 適応型メッシュ更新モジュールは、現在のメッシュの適合性を計算し、誤差の大きいすべてのメッシュを分割更新します。システムはユーザーが定義した誤差許容値に達するまで、この再メッシュと解の計算を反復します。
- グラフィック出力モジュールは、計算された解に関して、任意の代数的関数を操作し、輪郭線図、面、ベクトルまたは高度なプロットを描きます。
- 画像データの出力 (6種類)
- BMP: Bit Map 画像形式
- EMF: (Windows版のみ) Microsoft Windows Enhanced Metafile
- EPS: Encapsulated PostScript
- PNG: Portable Network Graphics
- PPM: portable pixmap、バイナリの画像形式
- XPM: X PixMap、テキスト(ASCII)の画像ファイル形式
- データ出力モジュールは、簡単な表、完全な有限要素メッシュデータや、CDF あるいは Tecplot 対応のファイルを含む、多くの形式のテキスト出力を書くことができます。
- プロット・データの出力 (4種類)
CFD: netCDF version 3 形式
TABLE: アスキー表形式
TECPLOT: Tecplot用データ
VTK: VTK (Visualization Tool Kit) 形式 - プロット・データの入力 (1種類)
DXF: AutoCAD の DXF形式
- プロット・データの出力 (4種類)
記述文はどのようなものでしょうか?
問題の記述文は読み易いテキストファイルです。そのファイルの内容は、各ヘッダーで区別される一連の区分 (Section) から成ります。基本的な区分は次の通りです:

- TITLE – 問題の題で出力の再の説明ラベルとしても使われます。
- SELECT – FlexPDE の既定動作に対するユーザーの変更を指定。
- VARIABLES – ここに従属変数の名前を書きます。
- DEFINITIONS – 使用するパラメータ、関係式、関数等を定義します。
- EQUATIONS – 変数毎にそれと関係する偏微分方程式を記述します。
- BOUNDARIES – 計算対象の図形はこれを囲むように線分や弧で繋げて、図形領域の周囲を歩くように記述します。
- MONITORS と PLOTS – 希望するグラフィック出力をリストします。CONTOUR、SURFACE、ELEVATION または VECTOR プロットの組合せができます。
- END – これで記述文は完成です。
- コメントは記述文のどこでも記入できます。
- { } 中括弧で囲まれた中はコメントです。
- ! 感嘆符からその行末まではコメントです。
区分による記述文例として、正方形上の簡単な拡散方程式は次のように記述されます。
TITLE ‘Simple diffusion equation’
{ this problem lacks sources and boundary conditions}
VARIABLES
u
DEFINITIONS
K=3 {conductivity}
EQUATIONS
div(k*grad(u))=0
BOUNDARIES
REGION 1
START (0,0)
LINE TO (1,0)
TO (1,1)
TO (0,1)
TO FINISH
PLOTS
CONTOUR (u)
VECTOR (k*grad(u))
END
スクリプトの記述例
作成されるMesh
境界条件とはどういうものでしょうか?
適当な境界条件の指定は、PDE システムを解くうえで決定的なものです。FlexPDE 記述文では、境界条件は境界を記述する過程で表現します。境界条件の主要な型は VALUE と NATURAL です。
- VALUE (または、ディリクレ)境界条件は、その領域の境界上で変数が取らなければならない値を指定します。
- NATURAL (自然) 境界条件は、その領域の境界でのフラックス (flux:流量) を指定します。(NATURAL 境界条件の正確な意味は、その境界条件が指定される PDE に依ります。)
例えば、上記の拡散問題で、上下の辺の境界で固有値を、左右の辺の境界で流量(flux)ゼロの条件を加えると、その部分は次のようになります:
…
BOUNDARIES
REGION 1
START(0,0)
VALUE(u)=0 LINE TO (1,0) { fixed value o bottom }
NATURAL(u)=0 LINE TO (1,1) { insulated right side }
VALUE(u)=1 LINE TO (0,1) { fixed value on top }
NATURAL(u)=0 LINE TO FINISH { insulated left side }
…
VALUE または NATURAL 宣言文は、その宣言が変更されるまで以降の境界部分にも適用されることに注意してください。
インターフェース
FlexPDE のインターフェース
編集ウィンドウ
- これは標準的な NOTEPAD 型の編集ウィンドウで、選択された記述文ファイルの内容を示しています。通常の方法でスクロールや編集ができ、FlexPDE のキーワードは赤色で強調され、コメント部は緑色で、テキスト文字列は青色で表示されます。
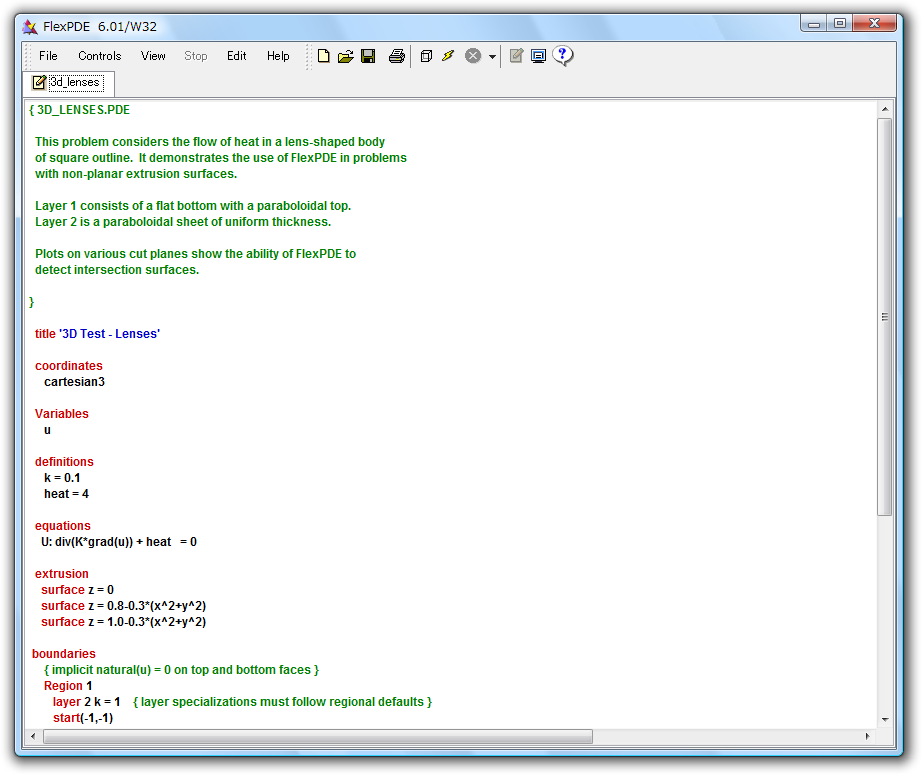
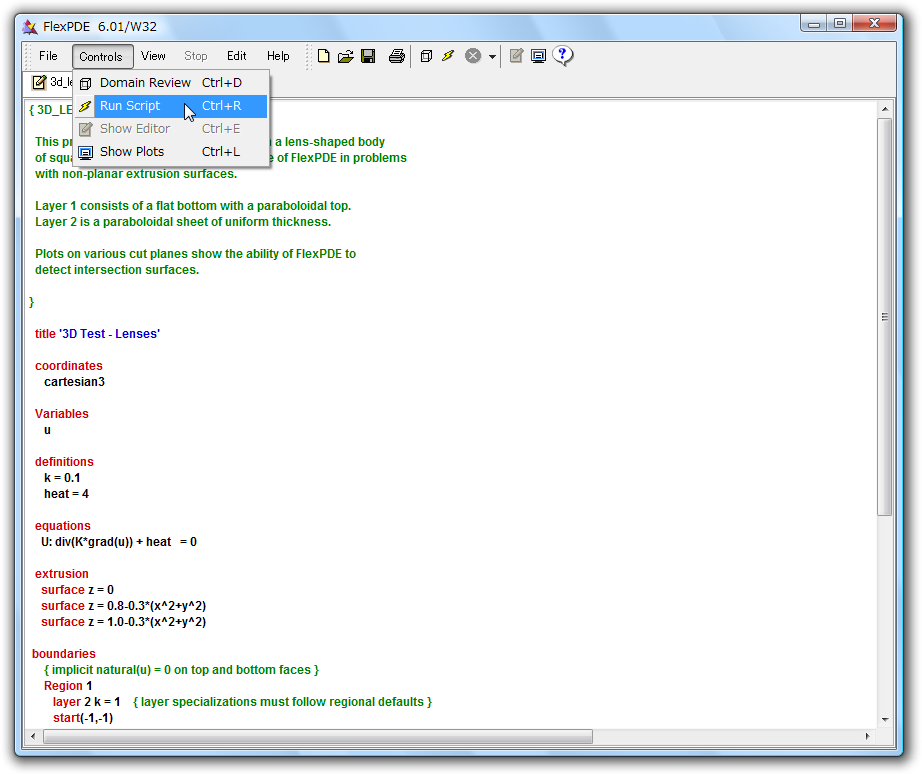
Run をクリックすると計算を実行します。
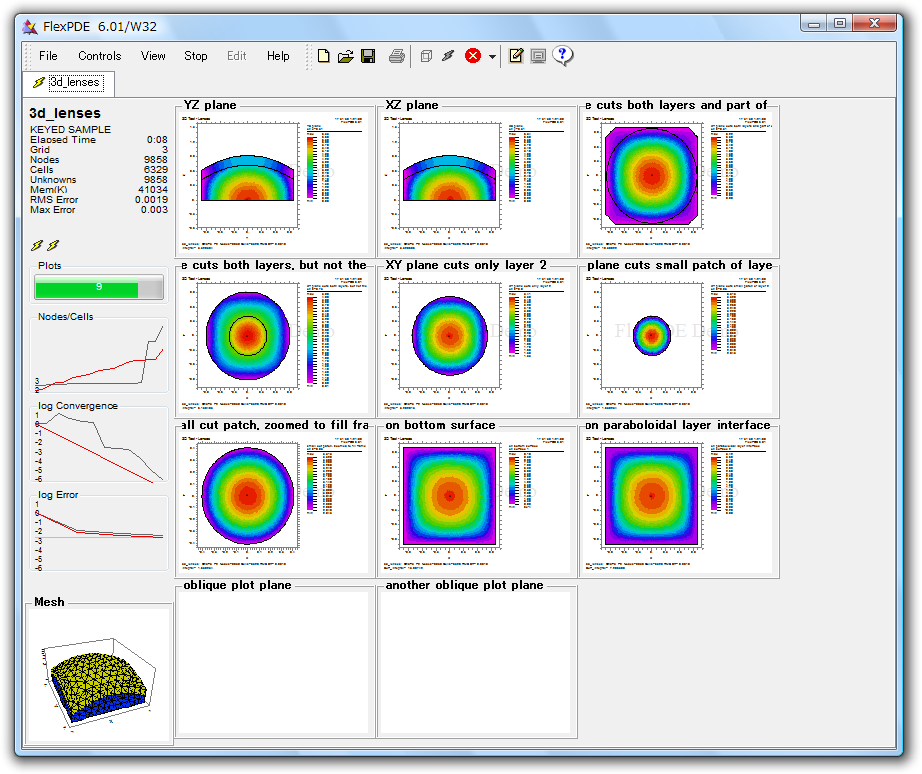
計算問題の実行中および完了画面
- 画面の左側は、Status ウィンドウで、実行中の状態の報告を時々刻々表示し、下側の Mesh ウィンドウには計算中のメッシュを小さく表示します。画面の右側は、サムネイルウィンドウになっており、記述文の PLOTS 区分又は MONITORS 区分で指定されたプロット項目を表示します。

Status ウィンドウ:
- Elapsed time ; この問題に費やされた経過時間
- Grid ; 現在までの再メッシュの回数
- Nodes ; 計算対象の総ノード数
- Cells ; 計算対象の全有限要素数
- Unknowns ; 全未知数 (ノード数 X 変数の数)
- Mem(K) ; 使用されているメモリ (キロバイト)
- RMS Error ; 現在の空間誤差 (RMS)
- Max Error ; すべてのセルにおける現在の最大空間誤差
PLOT ウィンドウ:
- 定常問題では、MONITORS 区分に記述された項目のみが実行中に表示されます。計算が完了すると、それらは PLOTS 区分で指定されたものに置き換わります。
- 時間依存問題では、MONITORS と PLOTS 区分のすべての項目が同時に表示されます。そして、記述文で時間指定された時刻順に更新されます。
- どのサムネイル・プロットを右クリックしても、その操作を選択できるメニューが現われます。
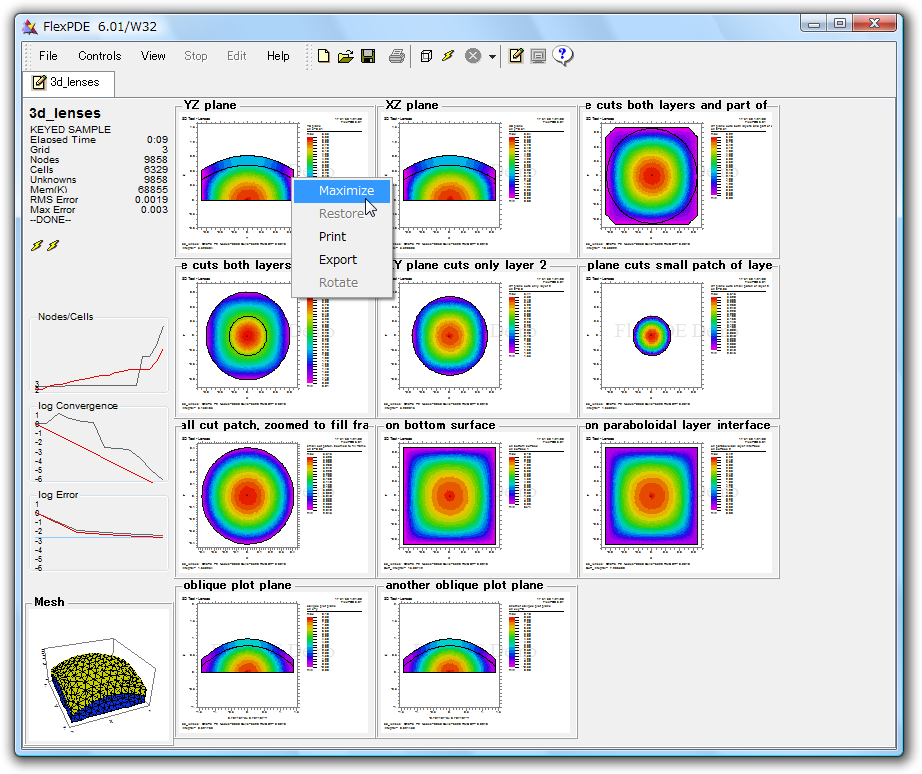
- Maximize
選択されたプロットを拡大して最大化します。 - Restore
最大化されたプロットをサムネイル画面に戻します。 - Print
標準のプリントダイアログを通じて、その画面を印刷します。 - Export
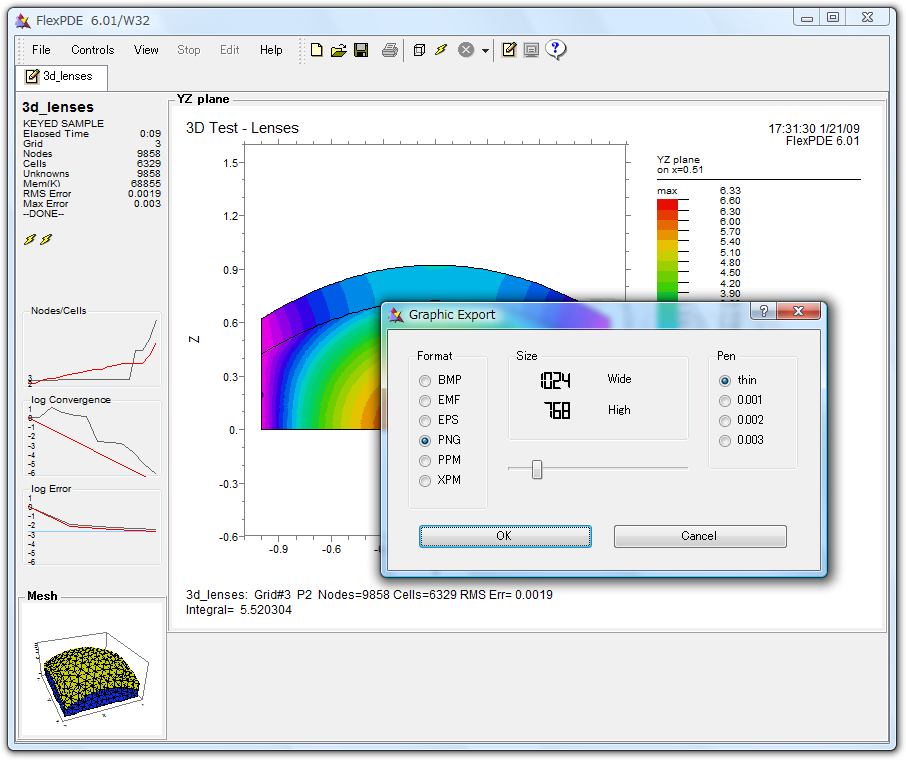
これは、この標準のフォーマット画像を他の使用目的で出力するための画像フォーマットを選択するダイアログを起動します。現在のところ、BMP、EMF、EPS、PNG、PPG、XPG が選択できます。ビットマップ(BMP、PNG、PPG、XPG)では、現在のスクリーンの分解能に依らずそのビットマップの分解能を指定できます。ベクトルフォーマット(EMF、EPS)では、分解能の指定は必要ありません。(FlexPDE は 5400 x 7200 の固定分解能です。)EPS は印刷に適した 8.5 x 11 インチの横型の PostScript ファイルを作成します。
プロット図のラベリング:
- 典型的な CONTOUR (輪郭線または等高線) プロットは次の例のようなものです:
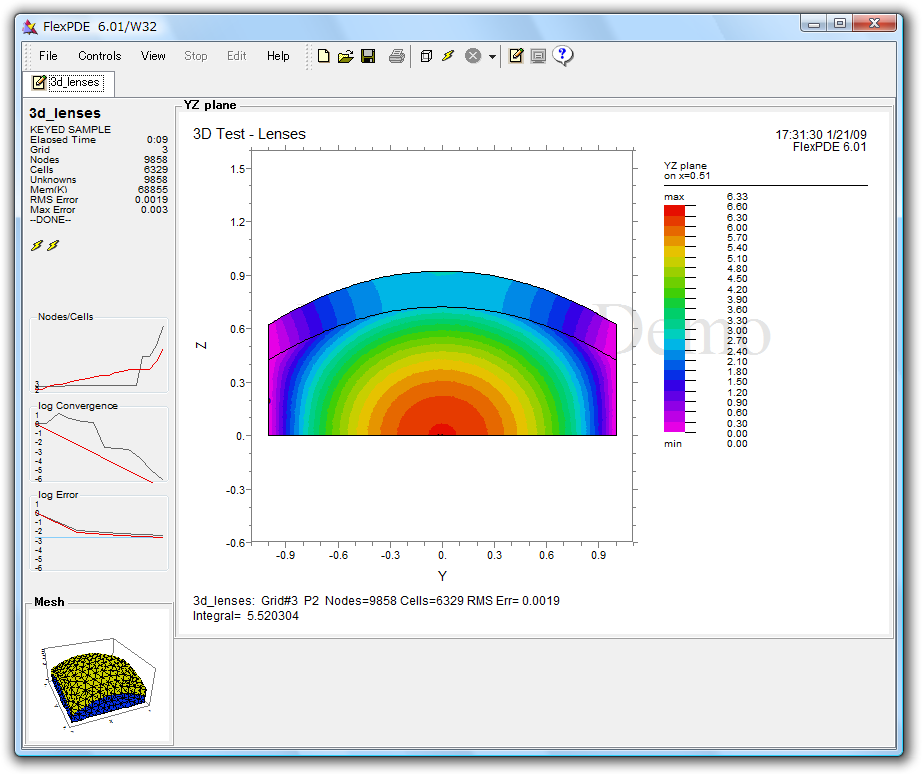
- 画面の最上部には、この問題のタイトルと、右端には実行された時刻と日付が、計算に使われた FexPDE のバージョンと共に表示されます。
- ページの下端には Status ウィンドウに表示された項目に似たこの問題のまとめが記録されます。
- 解析問題の名前、これまでに実行された再メッシュの回数、有限要素の基礎関数のベキ乗数(p2 = 2次、p3 = 3次)、ノード数、セル数、変数の相対誤差の RMS 値
- staged 機能を使用した問題では、stage 数も記録されます。
- 固有値問題では、モード数も記録されます。
- 時間依存問題では、問題の時刻とタイムステップも記録されます。
- また、FlexPDE は自動的に表示された曲線の下を積分し、その値を “Integral” として記録します。
- すべての指定された REPORT 項目は、最下部に1行で表示されます。
CAD、可視化ツールとの連携
DXF ファイル → FlexPDE
AutoCAD や AutoCAD LT などで作成された DXF 形式の形状データを、FlexPDE で読み込むことが出来ます。解析に必要な情報は、CAD 側で文字情報として予め付加しておくことも可能です。もちろん、2次元形状のみを CAD で作図し、FlexPDE で情報を付加していただけます。

→
- FlexPDE のユーザが DXF データを導入する利点
- FlexPDE では、LINE や ARC コマンドで形状を記述するため、複雑な形を定義するのは手間です。 DXF データを用いることにより、形状データの入力や修正が大幅に省力化できます。
- DXF を扱える CAD システムは多数あるため、部署間や業者間でデータの受け渡しが容易にできます。
- 形状を視覚的に把握できるため、問題の理解がスムーズに行えます。
- AutoCAD のユーザが FlexPDE を導入する利点
- FlexPDE を活用することにより、わずかな出費で、熱解析、振動解析、応力解析、電磁波解析といった、種々の解析を手軽に行うことが出来ます。
- 今まで蓄積された CAD データを生かせます (解析のために、新たに解析用のデータを作成する必要がありません)。
- ノートブックのような自由フォマットのテキストで、解析用のプログラムを記述でき、すぐに実行できます (コンパイルする必要がありません)。
- DXF データの形状記述の中に、0番目のレイヤー上にコメントとして、解析用のプログラムを記述できます。形状記述のデータと、解析用のプログラムを1つのファイルとして持てるため、データの管理が容易です。
FlexPDE バージョン 8 の新機能
- インターネット経由のライセンスオプションの向上 –
Auto-release オプション、multi-seat オプション、ライセンス状態のオンラインアクセスによる確認と管理。 - OpenGL プロット –
OpenGL を利用できる新しいセレクター GLGRID, GLCONTOUR, GLSURFACE 。 - メッシュの再接続 –
暗移動メッシュでメッシュの再接続を自動的に行なう新しいセレクター RECONNECT。領域ごとにさまざまな種類の再接続を制御できるため、必要に応じて再接続プロセスの制御を強化できます。Mesh Reconnection - 回転押出し (Rotational Extrusion) –
新しい ROTATION を使えば、Z 方向に押出す EXTRUSION ではなく、回転角で押出しを定義できます。2D 円筒状モデルを素早く 3D に変換できます! - 複素固有値 –
複素固有値解を生成するモデルを解くことができます。 - 明示的変数 –
指定した領域において、任意の変数を明示的な式に設定できます。 - SVG 形式のグラフィックエクスポート –
全てのプロットを SVG (Scalable Vector Graphics) 形式でエクスポートできます。 - 周期的境界条件の一般化 –
周期的境界条件のマッピングで変数を交換できるようになりました。ベクトル成分の交換に最適です。 - 双曲線関数の追加 –
双曲線関数に COTH, SECH, CSCH を追加しました。 - 新しい距離関数 –
新しい EDGE_DISTANCE 関数は名前付きパスに沿った距離を計算します。 - 新しいユーティリティ関数 –
新たに追加された連続導関数 FLOOR および CEILING 関数。Max と Min の変わりに使います。 - その他の内部的改善 –
TRANSFER ファイル形式の改善、エラー測定の改善、デバッグファイルにおけるパラメータ/方程式のサマリーの改善、ニュートン収束を妨げとなる不連続ヤコビアン診断機能の改善。
動作環境
FlexPDE 8 動作環境
| 64 bit (32 bit はありません) |
| Windows | Windows 64 (Windows 7/8/10/11) (AMD64 with EM64T) |
| Linux | Linux86 64 (AMD64 with EM64T) |
| Macintosh | Mac OS X 10.13 以降 (Mac版のインストーラはベータ版です。) |
FlexPDE のライセンスの種類について
FlexPDE のライセンスには、次の2つのタイプがあります。
- Single License
- FlexPDE を単独の PC でのみ利用できます。
- Network License
- FlexPDE 用ライセンス・サーバーで、ライセンス・デーモンを走らせます。
- 任意の PC が、ライセンス・サーバーに有効なライセンスを問合せて、購入したライセンス数の範囲内最大10ユーザーで、FlexPDE を同時使用ができます。
プロテクト・キーの種類について
- Single License のプロテクト・キーは、インターネット・キーとなります。ご要望があれば、ドングルまたはマシンの CPU に基づくソフトウェア・キーを発行することも可能です。
- Network License のプロテクト・キーは、ドングルとなります。USB Port キー、Parallel Port キーのどちらかをご選択ください。
ライセンス
FlexPDE 8 のライセンス管理方法
FlexPDE には、以下の 3 種類のライセンス管理方法があります。
インターネット・キー
FlexPDE Professional をインターネット経由でアクティベートする、基本のライセンス管理方法です。このライセンス管理モードでは、FlexPDE の実行をある特定のコンピュータに限定するテキスト・キーが生成されます。キー認証のための定期的なインターネットアクセスが必要になります。キーは簡単に、ひとつの PC から開放して、別の PC で再アクティベートすることができます。
| ※プロキシ・サーバーを経由したインターネットアクセスが FlexPDE-6.08 以降可能となりました。プロキシ・サーバーを経由される場合は、開発元から最新バージョン取得後、プロキシ・サーバーの設定をお願いいたします。 |
インターネット・キー・タイプのインストール方法:
ドングル
FlexPDE Professionalは、ポータブルUSBハードウェアキー(ドングル)を使用するように設定できます。 以前のドングルとは異なり、このドングルはローカルモードとネットワークモードの両方で使用できます。
| ※ このライセンス管理方法では、ドングル (有償) の購入が必要になります。 ※ v6より前のバージョンのHASPドングルはv8にアップグレードできないため、新しいCodeMeterドングルを購入する必要があります。 |
ソフトウェア・キー
特別な要望があった場合、テキスト・キーによって、FlexPDE Professional の実行をある特定のコンピュータに限定することも可能です。ソフトウェア・キーは指定 PC に固有のもので、他の PC では使用できません。
| ※ 通常は、ソフトウェア・キーではなく、インターネット・キーを使用されることをお勧めします。特別な理由がある場合のみ、ご提供いたします。 ※ PC を変更された場合、購入後一年以内であれば、一回に限り無料で新しいキーが再発行されます。それ以降の再発行は有料となりますので予めご承知おきください。 |
ソフトウェア・キー・タイプのインストール方法:
ライセンス管理方法の変更について
使用中のライセンス管理方法を変更する場合は、弊社 (soft.sales@hulinks.co.jp) までお問い合わせください。
| ※ 他の管理方法からドングルまたはネットワークドングルへ変更する場合は、ドングルを別途ご購入いただく必要があります。 |
アップグレードについて
ご指定が無ければ、継続して同じライセンス管理方法をご利用いただきますが、他のタイプへ移行することも可能です。ご注文時にお申し出ください。
| ※ 他の管理方法からドングルまたはネットワークドングルへ変更する場合は、ドングルを別途ご購入いただく必要があります。 |
トライアル
FlexPDE のデモ版と評価版について
FlexPDE には、デモ版と評価版があります。デモ版、評価版ともダウンロードするモジュールは同じですが、ライセンス・キーのあり/なしでご利用できる機能に違いがあります。
- デモ版:ライセンス・キー なし
サンプルの内容について動作を確認できますが、サンプルの内容の修正は一切できません - 評価版: 評価ライセンス・キーが必要です
評価期間は 30日です。正式版 と 同じ内容で動作を確認できます
デモ版/評価版は下記申請フォームより、備考欄に「デモ版」か「評価版」かをご記入のうえ、お申し込みください。
デモ版お申込み
製品価格
※ 製品価格は、下記のお見積もりフォームよりお問い合わせください。
お見積り・ご購入
サポート
FlexPDE サポート情報
開発元へのリンク
- オンライン HELP
http://www.pdesolutions.com/help/index.html - 関連書籍:FREE の PDF をダウンロードできます。
http://www.pdesolutions.com/bookstore.html
