FlexPDE：有限要素法・数式処理内蔵の偏微分方程式汎用ソルバー

FlexPDE：有限要素法・数式処理内蔵の
偏微分方程式汎用ソルバー

1. 主な特徴
2. インストレーション
3. 記述ファイル
4. 例題
   1. 1変数関数のプロット
   2. 2変数関数のプロット：ラプラス方程式
   3. 2D 粘性流体の速度および速度ベクトル （連立問題）
5. 内蔵されている有限要素法の概要

• 資料：FlexPDE が内蔵する有限要素法
  1. Finite Element Methods, PDE Solutions, Applications of FlexPDE, Vol.1, Revision 1
  2. Appendix: Principles of Finite Element Analysis (Gunnar Backstrom, Fields of Physics)

FlexPDE は米国 PDE Solutions (http://www.pdesolutions.com/) のソフトウエア製品で、偏微分方程式と条件を指定するだけで、解が得られます。通常、所与の偏微分方程式群を差分法あるいは有限要素法を用いて、近似式に展開し、これをプログラミングする必要がありますが、FlexPDEは有限要素法による展開を自動的に実行して、解を出してくれる偏微分方程式の汎用ソルバーです。

近似式への展開は最も時間もかかり、神経を使うところで、大抵のバグは、展開式の間違いに起因することを考えますと、所与の式を数式処理によって展開し、解を出してくれる機能は大変便利です。問題を解く立場からすれば、これが非常に理想的であることは言うまでもありません。

市場には、数式処理ソフト、偏微分方程式を解くツールは各種ありますが、この両者を一体化したツールは、FlexPDE が唯一ではないかと思います。

FlexPDE は別に偏微分方程式のみに特化しているわけではなく、これ以外の方程式とその n 次微分あるいは偏微分についても扱うことができますが、有限要素法がいずれの場合でも内部で適用されています。

なお、FlexPDE の説明書としては、PDE Solutions が提供するマニュアル、HELP 以外に Gunnar Backstrom, Fields of Physics by Finite Element Analysis, GB Publishing, 2002 があります。著者はスエーデンのウプサラ大学の研究者で、ユーザとしての立場から、電磁気および熱に関する広汎な問題を FlexPDE でどのように解くかを説明しており、実践的なマニュアルとしても使用できます。本書は、PDE Solutions のサイトから無料でダウンロードできます。

それでは早速、FlexPDEのツアーに出かけましょう。

1. 主な特徴

1. １次および 2次の偏微分方程式を 2次元、3次元座標で解けます。2次以上の高次についても扱えますが、この場合は、中間変数を用いて、高次微分または偏微分を表現します。
2. 定常状態、時間依存、その混合のいずれも扱えます。また、固有値問題も扱えます。
3. 任意数の連立方程式を扱えますが （連成問題）、その規模は、走行するマシーン能力に依存します。
4. 線形、非線形の両方を扱えます。非線形システムは修正ニュートン・ラフソン法で解いています。
5. 異なる物体につき、任意数の領域を定義できます。定義する変数は、物体上で連続とします。微分のジャンプ条件は、偏微分方程式システムの記述で指定できます。

2. インストレーション

インストレーションは至って簡単です。入手したライセンス・ファイルをインストールでできた FlexPDE のルート・ディレクトリに格納して起動すれば、全機能が使用可能となります。ライセンス・ファイルの指示で「ライセンス・ディレクトリに格納すること」といったことが書いてありますが、これは無視して、ルート・ディレクトリに格納すればこれで OK です。

3. 記述ファイル

まず、FlexPDE を起動して New を選択すると下記のようなエディタ画面が表示されます。ユーザは、必要なところを記入し、不要な項目は削除して、実行すれば、結果が図示され、実行経過が示されます。FlexPDE は日本語化されていませんが、下記エディタ画面各項の意味はおおよそ理解できるのではないでしょうか。

なお、不要な部分を削除しないで、Run するとエラーが発生するので、不要部分の削除を忘れないようにしてください。また、{......} で囲うとコメントをかけます。エディタを利用して作成したスクリプトをディスクリプタ・ファイル （記述ファイル） といいます。

ここで、各項目を一般的に説明しても、退屈なだけでしょうから、早速例題をやってみましょう。

4. 例題

例題１： 1変数関数のプロット

f=sin(x)+x*cos(x)、f の一次微分、f の二次微分の３つを同時にプロットする問題です。

この問題を解く場合に必要なことは、関数、一次微分、二次微分を定義し、さらにプロットする範囲を指定することです。

関数の定義は DEFINITIONS のところで、f=sin(x)+x*cos(x), fx=dx(f), fxx=dxx(f) として行っています。FlexPDE は dx(f), dxx(f) をそれぞれ、関数 f の x に関する一次微分、二次微分として認識し、内部で数式処理を行います。

描画する範囲については、Lx=10, Ly=1 として、(-Lx,-Ly) を起点として ( START で指定)、ついで、(Lx,-Ly)->(Lx,Ly)->(-Lx,Ly) と反時計方向に描画するものとします （起点以後の指定は line 文で行っています）。

ついで、実際の描画を行う指定をします。これは PLOTS で行っています。

　記述ファイルは以下のようになります。

上記のように入力し、不要部分を削除して、Run をクリックすれば、下図が表示されます。a, b, c 各曲線が、関数 f、 一次微分、二次微分に対応します。

例題２： 2変数関数のプロット（ラプラス方程式）

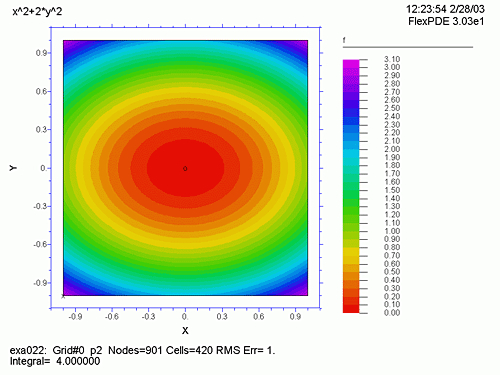
f = x² + 2y² として、以下の２変数関数をプロットします。

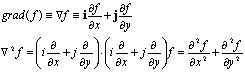
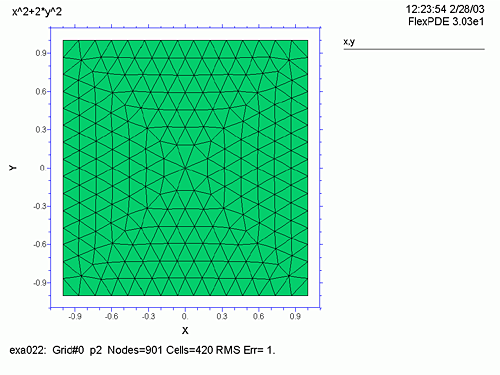
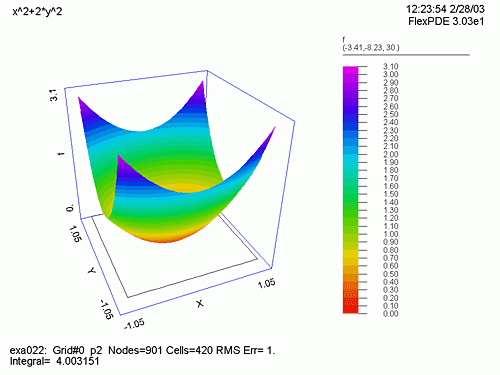
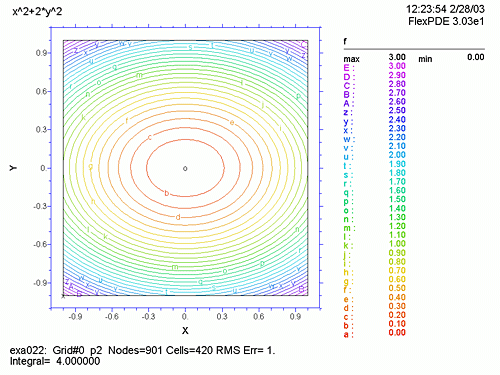
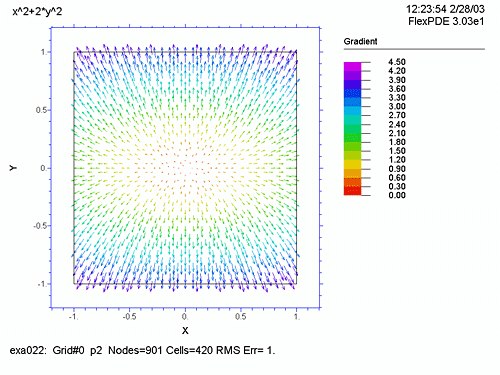
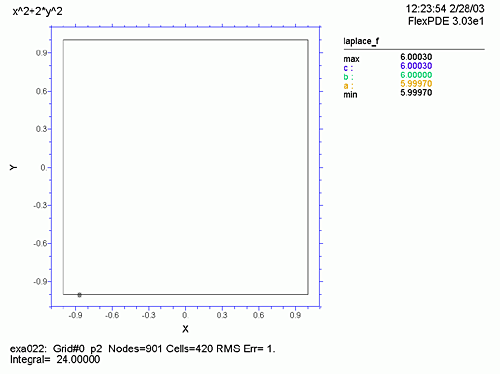
DEFINITIONS で上記３つの関数を定義します。grad(f) において i,j は単位ベクトルであり、これを表現するには vector(dx(f), dy(f)) とします。また、次のラプラス方程式の2次微分の式は dxx(f)+dyy(f) と表現します。BOUNDARIES で例題１同様、図形の境界とプロット順を指定し、PLOTS でプロットすべき図を指定します。メッシュ分割状況 （grid）、f の曲面表示 （surface）、f の等高線図 （contour）、等高線図の線間を彩色した図 （contour(f) painted）、grad(f) のベクトル表示、ラプラス方程式の等高線図 （contour） の6種類をプロットします。

　その結果記述ファイルは以下のようになります。

ここで、Run をクリックすると、6つのグラフの縮小したものが、一度に表示されます。どれか特定のグラフ上でダブルクリックすると、そのグラフだけが、大きく表示され、ここで再度ダブルクリックすると、もとの縮小グラフに戻ります。

次に各グラフを見ていきましょう。

1. grid(x,y) によるメッシュ分割図
   f の領域 での三角形でのメッシュ分割状況を示しています。各メッシュの頂点および各辺の中点の値 （全部で 6個） が二次式による内部的が内挿されます。

   901 ノード、420 セルに分割されていることが、図下段の表示からわかります。

   
   
2. surface(f) による曲面表示

   グラフ上で右クリックして、Rotate を選択すると、左の小ウインドゥに視点のスケール （Az は y 軸回り、Po は x 軸回りの回転目盛り）が現れ、値を選んで、Redraw をクリックすると、回転図形が表示され、図の右側上に （視点座標 (x,y) および仰角 （度）） が数値で示されています。同じ色の個所は同じ値を持っています。色と値の関係は図の左に示されています。

   
   
3. contour(f) による関数 f の等高線図

   f の (x,y) 平面上での曲線群を示しています。左には色と値の関係および最大値、最小値も示されています。

   
   
4. 同上等高線図の線間を彩色したもの (painted 指定)
   
5. vector(grad_f) による grad(f) のベクトル図

   grad(f) のベクトル （傾きと大きさ（矢印の長さ）） 表示です。色の違いはベクトルの大きさに対応しています。

   
   
6. contour (laplace_f) によるラプラス方程式の等高線図

   曲線が１つもないのは、∇2 = 0 であるためで、ゼロでなければ、関数 f は調和関数ではないことになります。

例題３： 2D 粘性流体の速度および速度ベクトル （連立問題）

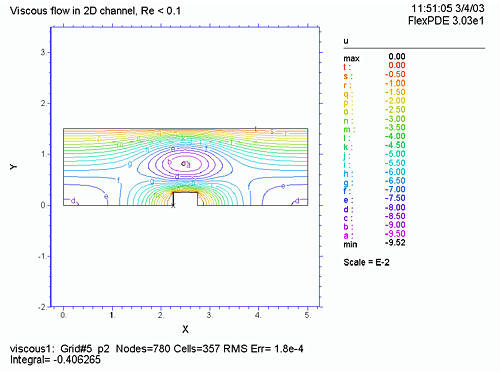
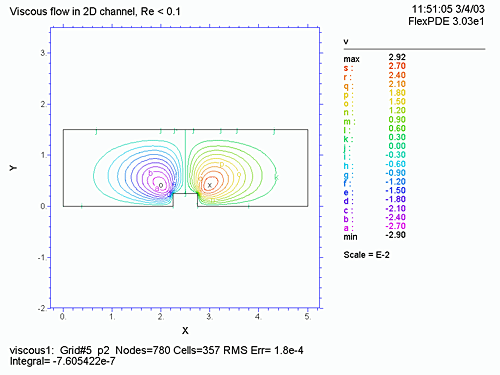
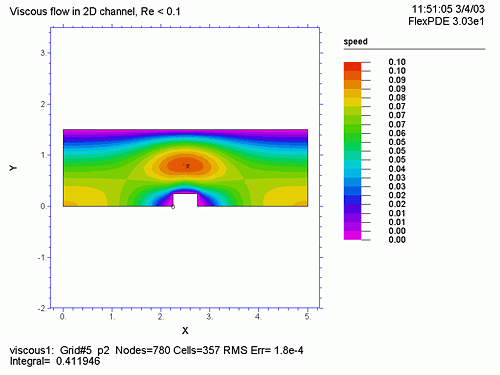
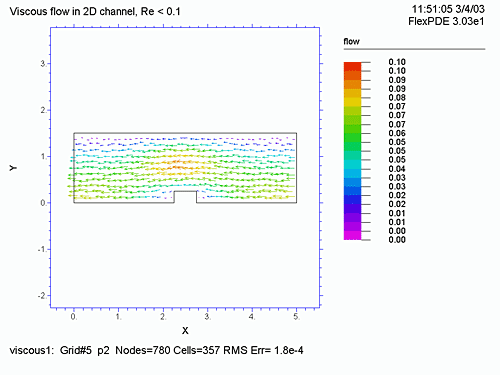
底辺に矩形の突起がある流管の 2D での速度ベクトルをナヴィア・ストークス方程式で計算します。

2D の定常非圧縮流れは、下記のナヴィア・ストークス方程式で表されます。

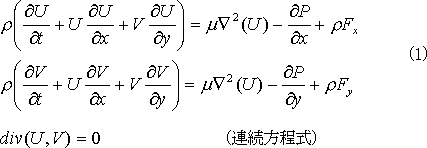
上式で、ρ は流体の密度、μ は粘性率、U, V は流体速度のそれぞれ、X, Y 成分、F_x, F_y は体積力のそれぞれ、X, Y 成分、P は圧力で、この式が更に必要となります。U の式 （一番上の式） を Y で微分し、連続方程式と連立させ、項を消去すると、下式が得られます。

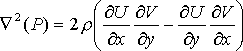
div(U, V)=0 であるので、圧力の式に自由に項を足してもよく、流体に抗する正の圧力項を加えます （負の圧力項は、物体の破壊を意味します）。その結果、

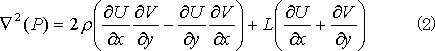
ここで L は、保存則を満足する十分「大きな」数に選ぶものとします。

記述ファイルの EQUATIONS の最初の2つの式は、(1) の両辺を μ で除し、かつ、 を考慮すれば得られます。つまり、

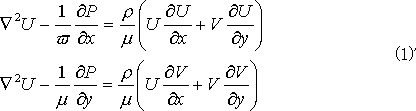
EQUATIONS には、(1)’ と (2) を指定しています。

初期条件は、INITIAL VALUES で、流体速度の x, y 成分 （U, V） および圧力を以下のように設定しています。

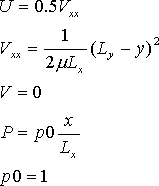
また、DEFINITIONS で、ρ=1, μ=1 としています。

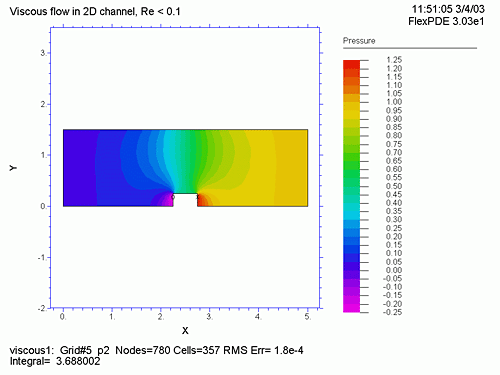
次に、BOUNDARIES では、領域の形状および各部における境界条件を value （ディリクレ条件） および load (ノイマン条件あるいは自然境界条件) で指定しています。たとえば、value(v)=0 はその個所において解 v をゼロと指定するものですし、load(p)=p0 は、その個所において、解 p を p0 と指定するものです。形状は、grid(x,y) による図を参照してください。

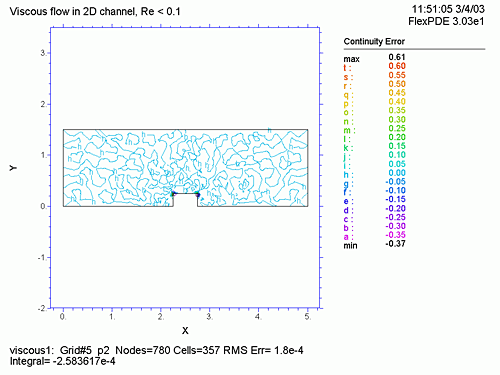
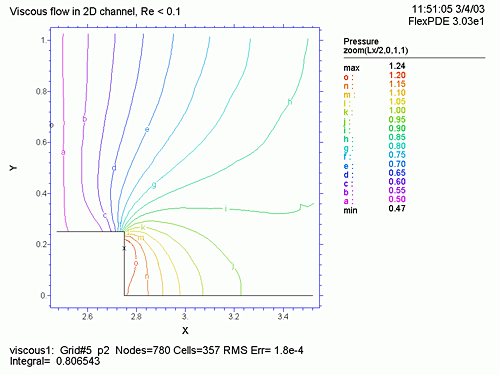
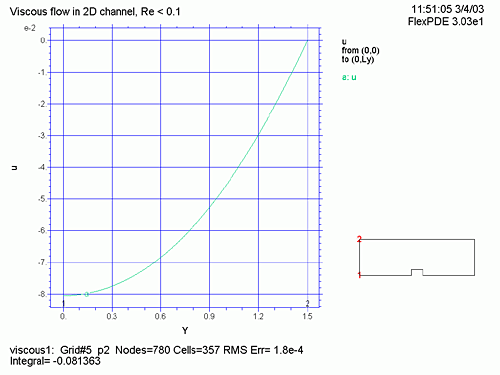
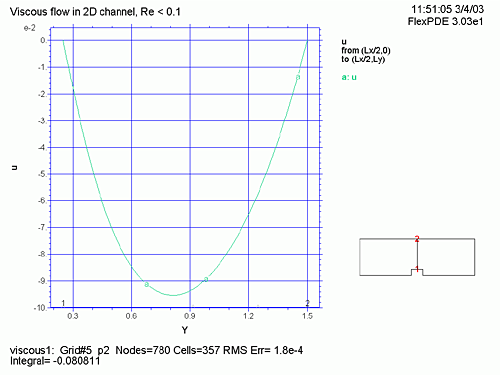
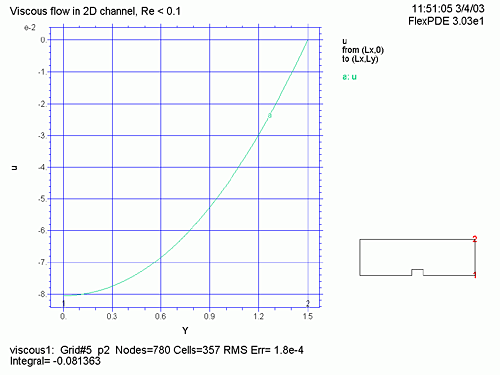
PLOTS では、メッシュ形状 （grid(x,y) ）、U, V、速度 （） の等速線図、圧力 (P) の等圧線図、U, V の流れのベクトル表示 （vector(u,v) ）、連続方程式に対する誤差 、流管の入り口、中央、出口における X 方向の速度などをプロットします。

上記記述ファイルは以下のようになります。

1. メッシュ分割状況（grid(x,y)）
   図のような領域 （BOUNDARIES で記述している） を 357 個の三角形に分割、ノード数は 780個になっています。また、適応型メッシュ分割を行っていることがわかります。図の右側から流体が入り、左側に出て行きます。
   
2. U （流速の X 成分） の等速線図 (contour(u))
   
3. V （流速の Y 成分） の等速線図 (contour(v))
   
4. 流速の等速線図 （contour (speed) painted）
   
5. 速度ベクトル （vector (u, v) ）
   
6. 等圧線図 (contour(p) painted)
   
7. 連続性方程式の誤差 (contour(dx(u)+dy(v) )

   全領域に渡って誤差がゼロ （h） であることが解ります。

   
   
8. 指定領域の等圧線図 (contour(p) zoom(Lx/2,0,1,1) )
   zoom の指定は zoom (x 座標、y 座標、幅、高さ) として行い、この領域のみの図を示します。
   
9. 出口における x 方向速度 vs. y 座標 (elevation(u) from (0,0) to (0,Ly))
   elevation は 2次元表示を行う機能を持ち、elevation(arg1,[arg2,...]) <経路>で指定します。
   経路は、from (x0, y0) to (x1, y1) などと指定します。上記の例では、原点から y 方向に線分 L_y を指定しています。従って、得られるグラフは、y 座標に対応する u の値がプロットされます。
   
   
   
10. 中央における x 方向速度 vs. y 座標 (elevation(u) from (Lx/2,0) to (Lx/2,Ly))
    
    
    
11. 入り口における x 方向速度 vs. y 座標 (elevation(u) from (Lx,0) to (Lx,Ly))
    

5. 内蔵されている有限要素法の概要

重み付き残差法、適応型メッシュ、二次または三次多項式での内挿、部分積分方式、初期値問題には、BDM (Backward Difference Method by C.W.Gear) を採用しています。ユーザが解の精度を指定することもできます (SELECT ERRLIM)。

より詳細は、

1. Finite Element Methods, PDE Solutions, Applications of FlexPDE, Vol.1, Revision 1
2. Appendix: Principles of Finite Element Analysis (Gunnar Backstrom, Fields of Physics)

の日本語訳をご参照ください。