世界で最も信頼できる最新技術計算システム
Mathematica は 30 年以上に渡り、最新の技術計算を定義し、世界中の開発者、教育者、学生等、何百万人ものユーザに重要な計算環境を提供してきました。
優れた技術的機能と使いやすさで広く賞賛されている Mathematica は、継続的に拡張される単一の統合システムを提供し、技術計算を広く深く取り扱うことを可能にします。最新のデスクトップシステムすべてでネイティブに利用できるだけでなく、あらゆる Web ブラウザを介してクラウドでシームレスに利用できます。
最新の技術計算では他に匹敵するものがありません
30年に及ぶ精力的な開発努力と一貫したビジョンによって、Mathematicaは規模の大きさで群を抜いており、今日の技術計算環境とワークフローを独自の方法でサポートします。

すべてが統合された巨大システム
Mathematica は技術計算のあらゆる分野を扱うための組込み関数をほぼ 6,000 個も備えています。このすべてが、一緒に使えるように注意深く設計されており、完全に統合された Mathematica システムに含まれています。
想像を超えるアルゴリズムパワー
Mathematica にはすべての分野においてこれまでになくパワフルなアルゴリズムが組み込まれています。その多くは、ユニークな開発方法と Wolfram 言語独特の機能を使って Wolfram で作成されたものです。
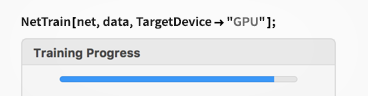
すべてが非常に強力
Mathematica は、すべての分野でのロバストで効率的なアルゴリズム、大規模問題を取り扱う機能、並列計算、GPU 計算等、非常に強力な機能を提供するように構築されています。
文書化とコード作成
Mathematica は Wolfram ノートブックインターフェースを使っています。これにより、テキスト、実行可能コード、動的グラフィックス、ユーザインターフェース等を含む豊かなドキュメント内で、すべての作業を整理することが可能になっています。
結果を最高の外観に
高度な計算美学を備え、そのデザインで受賞に輝いたこともある Mathematica は、結果を見やすく提示します。最高級のインタラクティブな可視化および出版品質のドキュメントを即座に作成します。

シームレスにクラウドと統合
Mathematica がクラウドとシームレスに統合された結果、ユニークでパワフルなクラウドとデスクトップのハイブリッド環境における共有やクラウド計算等が可能になりました。
15 万を超える例題
どのようなプロジェクトを始めるのであれ、ほとんどの場合、ドキュメントセンターの 15 万以上の例題、Wolfram デモンストレーションプロジェクトの 1 万を超えるオープンコードのデモンストレーション、その他多数のリソースからヒントを得ることができます。

数や数学だけではなくすべて
30 年の開発の上に構築された Mathematica はニューラルネットワーク、機械学習、画像処理、幾何学、データサイエンス、可視化等を含むすべての技術計算の分野において、卓越した機能を備えています。
これまで以上に高レベル
Mathematica はスーパー関数やメタアルゴリズム等の高レベル環境をできる限り自動化して提供するので、作業が効率的に進められます。
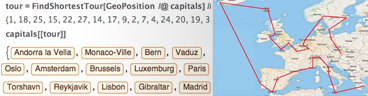
パワフルで使いやすい
Mathematica は注意深く設計された Wolfram 言語の他、アルゴリズムのパワーも利用して、予測サジェスチョン、自然言語入力等を備えた非常に使いやすいシステムを作成します。
意味の分かるコード
Wolfram 言語は、直観的な英語に似た関数名を持ち、設計も一貫しているため、読んだり、書いたり、学んだりすることが非常に簡単です。
現実世界のデータを即座に取得
Mathematica は、何千もの分野における 1 分単位で更新される現実世界のデータを含む Wolfram Knowledgebase へのアクセスを提供します。

何にでも接続
Mathematica は、180 以上のファイル形式、他の言語、Wolfram Data Drop、API、データベース、プログラム、モノのインターネット、デバイス、配布された Mathematica のインスタンスを含め、何にでも接続できるよう設計されています。
適用対象
Mathematicaは画期的なWolfram言語を基盤としています。
機能一覧
コアとなる主な分野
新機能
Mathematica 14.3 の新機能
バージョン14.3では、ダークモードへの完全サポートが追加され、ダークモードとライトモードの両方の環境のために、新たに汎用性のある色が設計、導入されました。
バージョン1.0で開始された非可換代数の実装が完了し、ヒルベルト変換、Lommel関数、新しい行列分解も追加されました。
可視化機能も強化され、ListFitPlotによる自動曲線フィット、曲面プロット関数、ベクトルベースの地図、メッシュ処理ツールが利用可能になっています。
その他の主な追加機能には、測地計算、AIワークフローの編成のためのLLMGraph、大幅に高速化されたPythonとRの統合、表形式データ操作のためのColumnwiseCombine、システムモデルの検証ツール、Markdown形式でのエキスポートのサポート等があります。
Mathematica 14.3 の新機能情報(一部):
- 無限の循環列を表現するCyclic
- LLMGraphとLLMGraphSubmitを使った、複数のLLM生成ステップのスケジュールと統合
- 学習なしで動作するようになった多くの特徴抽出器
- LocalModelFitを使った、局所的な多項式回帰の実行
- KernelModelFitを用いた平滑化カーネルによる関数近似
- 非可換代数を表現し、そのような代数における多項式の演算を行うための複数の関数の追加:
NonCommutativeAlgebra、GeneralizedPower、Commutator、Anticommutator、NonCommutativeExpand、NonCommutativeGroebnerBasis、NonCommutativePolynomialReduce等 - 対角化可能な行列の固有値分解を計算するEigenvalueDecomposition
- 行列のフロベニウス分解(ブロック随伴)を計算するFrobeniusDecomposition
- 多項式行列のエルミート分解を行うPolynomialHermiteDecomposition
- 多項式行列のスミス分解を行うPolynomialSmithDecomposition
- 関数のヒルベルト変換を計算するHilbertTransformおよび逆ヒルベルト変換を計算するInverseHilbertTransform
- 第一種および第二種のLommel関数および修正Lommel関数の追加:LommelS1、LommelT1、LommelS2、LommelT2
- 複数のTabularオブジェクトを統合し、共通の列の値を比較するためのColumnwiseCombineの追加
- Tabularに対するスタイル設定、および個々の要素のハイライト表示のためのオプションの追加
- ベクトル地図、新しい幾何エンジン、高速データアクセスに対応するようにアップデートされたGeoGraphics
- 生体高分子を三次元で重ね合せるBioMoleculeAlign
- 原子や結合を特性値に基づいて着色するMoleculeValuePlotおよびMoleculeValuePlot3D
- 分子間の特徴距離を計算するMoleculeFeatureDistance
- 領域内の2点間の最小弧長を求めるShortestCurveDistance
- 領域内の2点間を結ぶ最小弧長曲線を求めるFindShortestCurve
- 領域上の点におけるガウス曲率を計算するRegionGaussianCurvature
- 三角形の数を削減することでメッシュを簡略化するSimplifyMesh
- ノイズを除去することでメッシュを平滑化するSmoothMesh
- 曲面上で関数の等高線プロットを作成するSurfaceContourPlot3D
- 曲面上で関数の密度プロットを作成するSurfaceDensityPlot3D
- 領域内で特定の関心領域を強調するHighlightRegion
- フィット曲線と一緒にデータをプロットするListFitPlot、ListFitPlot3D
- システムモデルの設計仕様を検証するSystemModelValidate
- SystemModelのための時間設計仕様言語の導入と、それに対応するSystemModelAlways、SystemModelSustain、SystemModelUntil、SystemModelDelay
- 制御系オブジェクトにおける、微分方程式等の広範な特性のサポート
- 制御系の設計関数における、文書化と理解のためのブロック線図特性の提供
- 手ブレのある動画を安定化するVideoStabilize
- MeanFilterやGaussianFilter等の画像フィルタ関数が、フレーム単位で動画にフィルタを掛け、動画に直接対応
- 式およびノートブックのエキスポートにおけるMarkdown形式のサポート
- JSONLines形式に対するImportおよびExportのサポート
- ノートブックにおけるダークモードのサポート
- StandardRed、StandardGreen、StandardBlue、DarkRed、DarkGreen、DarkBlue等の新しい名前付きの色の追加
- ExternalEvaluatorObjectによる評価システムの記号的表現の追加
- 現在利用可能な外部評価システムを見付けるExternalEvaluators
計算カーネルの拡張性
Mathematica には、マルチコア CPU の PC の性能をフル活用できるように計算カーネルが装備されており、ご利用するマシン構成 (シングルマシン、ネットワーク、Web 等) やコア数に応じ、柔軟に拡張できます。
アドオン
Wolfram Research の開発者だけでなく、様々な分野の専門家 (航空、土木、機械、電気工学、財務、光学、天文学、物理学等) 達が開発した Mathematica アプリケーションが利用可能です。
サブスクリプション/サービス
アップグレードや、クラウドアクセス等を含むサブスクリプションで、生産性を最大限にし、ライセンスを最新の状態に保つことができます。
動作環境
Wolfram Research社サイトをご覧ください。
- System Requirements
http://www.wolfram.com/mathematica/system-requirements.html
ライセンス
ライセンス種別について
シングルユーザーライセンス
シングルユーザーライセンスは、一人のユーザーに一つのライセンスが提供されるライセンスオプションです
(一つのライセンスにつき、アクティベーションキーは二つ)。
アクティベーションキー一つにつき、一台のマシンにインストールできます。
ネットワークライセンス
ネットワークライセンスは、ネットワーク内の任意のマシンで Mathematica をご利用いただけるライセンスオプションです。
お申し込みいただいたライセンス数のMathematicaをネットワーク上で同時に起動することが可能で、複数のユーザーが複数のマシンでMathematicaライセンスを利用することができるようになります。
ライセンスを管理するライセンスサーバー(Network License Manager)と、同時起動に必要なクライアント (Network Seat) で構成されます。
ご購入例:
ネットワーク環境で Mathematica を 5 ライセンス同時起動したい場合は
Network License Manager × 1 + Network Seat × 5
が必要です。
サイトライセンス
大学や企業などでまとめてご利用時のライセンスです。
買取型の数量割引や、リース型等、いくつか種類があります。
詳しくは、営業部(soft.sales@hulinks.co.jp)までお問い合わせください。
ユーザー種別について
一般
企業・個人向けの商用ライセンスです。
個人所有のコンピュータまたは所属機関所有のコンピュータで利用することができます。
官庁
官公庁・独立行政法人・国立研究開発法人向けのライセンスです。
個人所有のコンピュータまたは所属機関所有のコンピュータで利用することができます。
商用に使うことはできません。
教育
大学・大学共同利用機関法人向けのライセンスです。
個人所有のコンピュータまたは所属機関所有のコンピュータで利用することができます。
企業、官公庁・政府系機関の研究、および企業、官公庁・政府系機関、非営利団体のコンサルティングに使うことはできません。
中/高/短大
中学校・高等学校・高等専門学校・短期大学向けのライセンスです。
個人所有のコンピュータまたは所属機関所有のコンピュータで利用することができます。
商用に使うことはできません。
学生用
学生向けのライセンスです。
個人所有のコンピュータで利用することができます。
商用に使うことはできません。
購入時に学生証のコピーが必要です。
パーソナル
趣味等の非営利目的で個人的に使えるライセンスです。
個人所有のコンピュータで利用することができます。
所属団体の業務、研究、教育、論文作成、商業目的等の使用はできません。
シングルユーザーライセンス ライセンス別比較表
| ライセンス | 一般/官庁/教育/中高短大 | 学生用 | パーソナル |
|---|---|---|---|
| 計算カーネル | 8個 | 4個 | 4個 |
| Wolfram | Alpha API Calls | 12000回/月 | 6000回/月 | 6000回/月 |
計算カーネル: CPUを使った並列計算処理するときの最大の同時起動カーネル数になります。並列処理で大量な計算処理の時、このカーネル数が多いほど効率的に時間を短縮することができます。Mathematica Core Extensionをお求めになることで計算カーネルを拡張し、8コアを超えるシステムに対応させることができます。
Wolfram | Alpha API Calls:WolframAlpha の機能や管理するデータなどを、外部の他のプログラムから呼び出して利用できる回数です。
トライアル
トライアルをご希望される方は、下記の デモ版申請フォーム よりご申請ください。
- 15 日間ご利用いただけます。
- Desktop版のMathematicaに加え、Cloud版のMathematica および Wolfram Notebook Assistant + LLM Kit をご利用いただけます。
デモ版お申込み
製品価格
一般
シングルユーザーライセンス
| 製品名 | 税込価格 |
|---|---|
| Mathematica Premium Plus Plan 一般 (年間ライセンス+永久Desktop Option) | ¥ 666,600 |
| Mathematica Premium Plan 一般 年間ライセンス | ¥ 333,300 |
| Mathematica Premium Plus Plan Renewal 一般 (※サブスクリプション更新) | ¥ 174,900 |
ネットワークライセンス
| 製品名 | 税込価格 |
|---|---|
| Mathematica 14.3J Network License Manager 一般 プレミアサービスプラス付 | ¥ 320,650 |
| Mathematica 14.3J Network Seat 一般 プレミアサービスプラス付 | ¥ 880,880 |
| Mathematica 14.3J Network License Manager 一般 プレミアサービス付 | ¥ 291,500 |
| Mathematica 14.3J Network Seat 一般 プレミアサービス付 | ¥ 800,800 |
ネットワークライセンスは、「Network License Manager」1 台と同時使用数分の「Network Seat」が必要です。
政府・地方公共団体
シングルユーザーライセンス
| 製品名 | 税込価格 |
|---|---|
| Mathematica Premium Plus Plan 官庁 (年間ライセンス+永久Desktop Option) | ¥ 598,400 |
| Mathematica Premium Plan 官庁 年間ライセンス | ¥ 299,200 |
| Mathematica Premium Plus Plan Renewal 官庁 (※サブスクリプション更新) | ¥ 165,000 |
ネットワークライセンス
| 製品名 | 税込価格 |
|---|---|
| Mathematica 14.3J Network License Manager 官庁 プレミアサービスプラス付 | ¥ 291,500 |
| Mathematica 14.3J Network Seat 官庁 プレミアサービスプラス付 | ¥ 800,800 |
| Mathematica 14.3J Network License Manager 官庁 プレミアサービス付 | ¥ 262,350 |
| Mathematica 14.3J Network Seat 官庁 プレミアサービス付 | ¥ 720,720 |
ネットワークライセンスは、「Network License Manager」1 台と同時使用数分の「Network Seat」が必要です。
教育
シングルユーザーライセンス
| 製品名 | 税込価格 |
|---|---|
| Mathematica Premium Plus Plan 教育 (年間ライセンス+永久Desktop Option) | ¥ 303,600 |
| Mathematica Premium Plan 教育 年間ライセンス | ¥ 151,800 |
| Mathematica Premium Plus Plan Renewal 教育 (※サブスクリプション更新) | ¥ 83,050 |
ネットワークライセンス
| 製品名 | 税込価格 |
|---|---|
| Mathematica 14.3J Network License Manager 教育 プレミアサービスプラス | ¥ 147,400 |
| Mathematica 14.3J Network Seat 教育 プレミアサービスプラス付 | ¥ 403,480 |
| Mathematica 14.3J Network License Manager 教育 プレミアサービス付 | ¥ 131,010 |
| Mathematica 14.3J Network Seat 教育 プレミアサービス付 | ¥ 358,600 |
ネットワークライセンスは、「Network License Manager」1 台と同時使用数分の「Network Seat」が必要です。
中学校/高校/短大
シングルユーザーライセンス
| 製品名 | 税込価格 |
|---|---|
| Mathematica Premium Plus Plan 中/高/短大 (年間ライセンス+永久Desktop Option) | ¥ 56,540 |
| Mathematica Premium Plan 中/高/短大 年間ライセンス | ¥ 28,270 |
| Mathematica Premium Plus Plan Renewal 中/高/短大 (※サブスクリプション更新) | ¥ 21,230 |
ネットワークライセンス
| 製品名 | 税込価格 |
|---|---|
| Mathematica 14.3J Network License Manager 中/高/短大 プレミアサービスプラス付 | ¥ 28,820 |
| Mathematica 14.3J Network Seat 中/高/短大 プレミアサービスプラス付 | ¥ 78,540 |
| Mathematica 14.3J Network License Manager 中/高/短大 プレミアサービス付 | ¥ 24,640 |
| Mathematica 14.3J Network Seat 中/高/短大 プレミアサービス付 | ¥ 67,320 |
ネットワークライセンスは、「Network License Manager」1 台と同時使用数分の「Network Seat」が必要です。
学生用
シングルユーザーライセンス
| 製品名 | 税込価格 |
|---|---|
| Mathematica 学生用 年間サブスクリプション (1 年間) | ¥ 10,560 |
| Mathematica 学生用 年間サブスクリプション (4 年間) | ¥ 27,280 |
パーソナル
シングルユーザーライセンス
| 製品名 | 税込価格 |
|---|---|
| Mathematica Personal Edition Premium Plus Plan (年間ライセンス+永久Desktop Option) | ¥ 54,560 |
| Mathematica Personal Edition Premium Plan 年間ライセンス | ¥ 27,280 |
| Mathematica Personal Edition Premium Plus Plan Renewal (※サブスクリプション更新) | ¥ 24,530 |
お見積り・ご購入
サポート
Mathematica 日本語版ご購入後の手続き
Mathematicaのダウンロードについて (シングル/サイト)
Mathematicaのダウンロードについて (ネットワーク)
インストール方法 (Wolfram Research 社のサイトへ)
テクニカルサポート情報
現在サポート対象であるバージョン (Wolfram Research 社のサイトへ)
TIPS
サポートお問い合わせ
導入事例
リスク解析に資する数理的手法の研究に不可欠なソフトウェア Mathematica : 確率シミュレーションや可視化ツールとしての活用
Mathematica は厳密な計算が可能である点が魅力です。数学的な理論の検証において非常に重宝しています。また、グラフ描画機能が優れており、図を作成する際には必ず利用しています。 (国立研究開発法人産業技術総合研究所 安全科学研究部門)
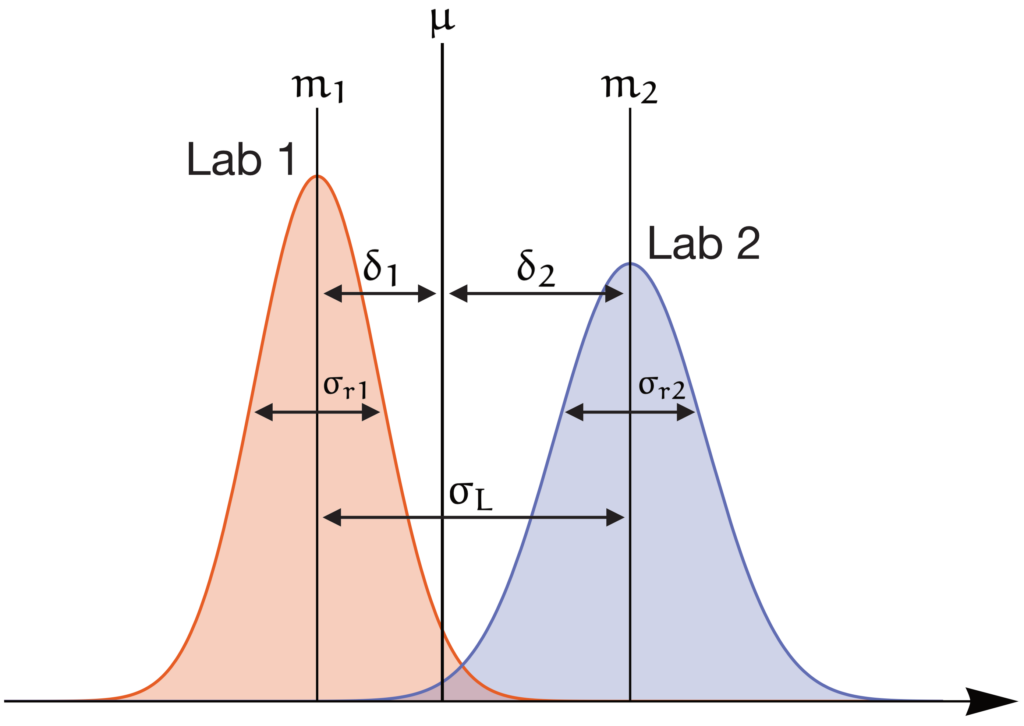
バージョンアップし続ける Mathematica とお付き合いして 36 年
常に時代とともにバージョンアップをし続け、LLM との連携もとてもいい動きです。また表現力が素晴らしく、いろいろな可視化ができるので、とても分かりやすい魅力的な資料を作ることができます。 (九州工業大学/大学院情報工学研究院 物理情報工学研究系)
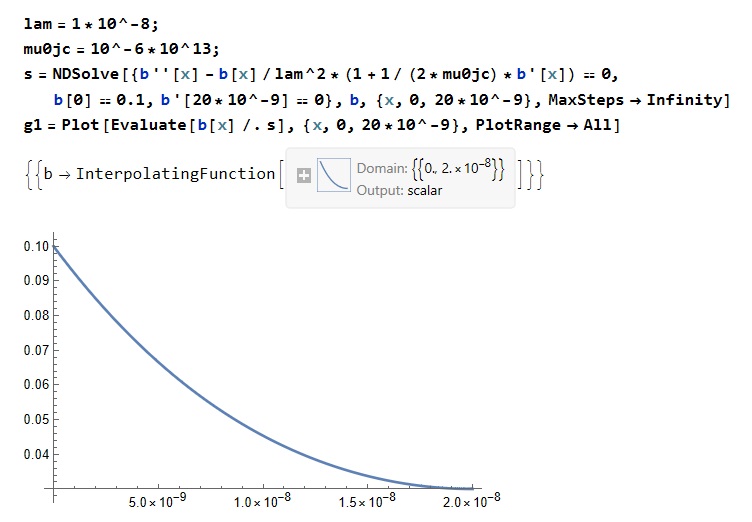
Mathematica で広がる研究の可能性 –医療放射線技術分野におけるデータ解析–
豊富な組み込み関数と初心者にも使いやすいインターフェースだと思います。アイデア次第で無限の可能性を秘めている List/Table 関数を使いこなして、多くの研究を Mathematica を用いて行いたいです。 (岡山大学学術研究院/保健学域 放射線技術科学分野)
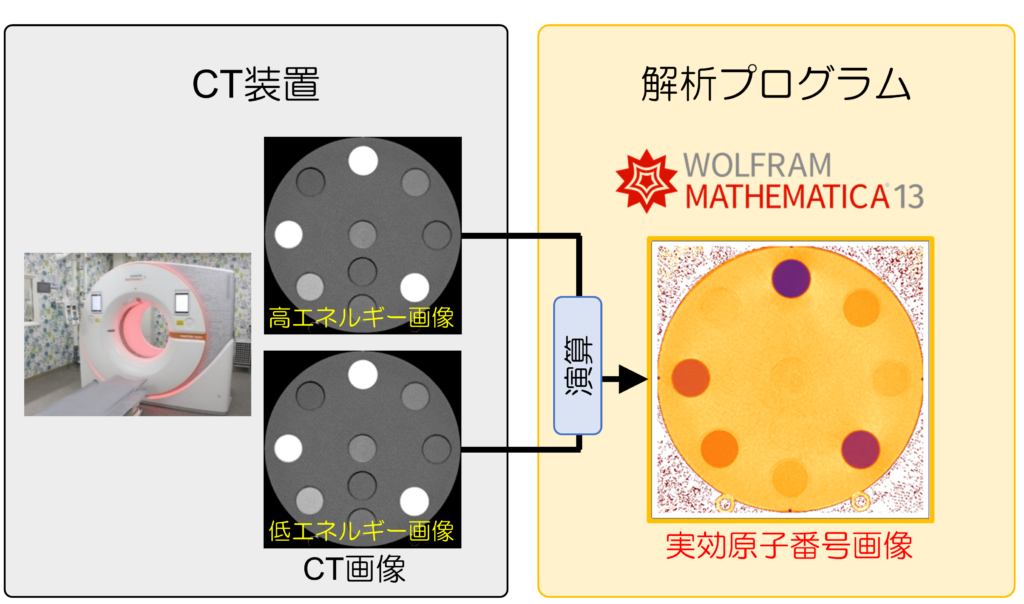
素粒子物理学の研究と教育及び参考書執筆
とても複雑な式の因数分解や、行列の固有値や固有ベクトル計算など様々なパターンの計算を安定した動作で計算でき、式を簡略化するコマンドもあって重宝しています。一方で数値計算、図やグラフの描画も強力です。 (東北大学/東北大学ニュートリノ科学研究センター)

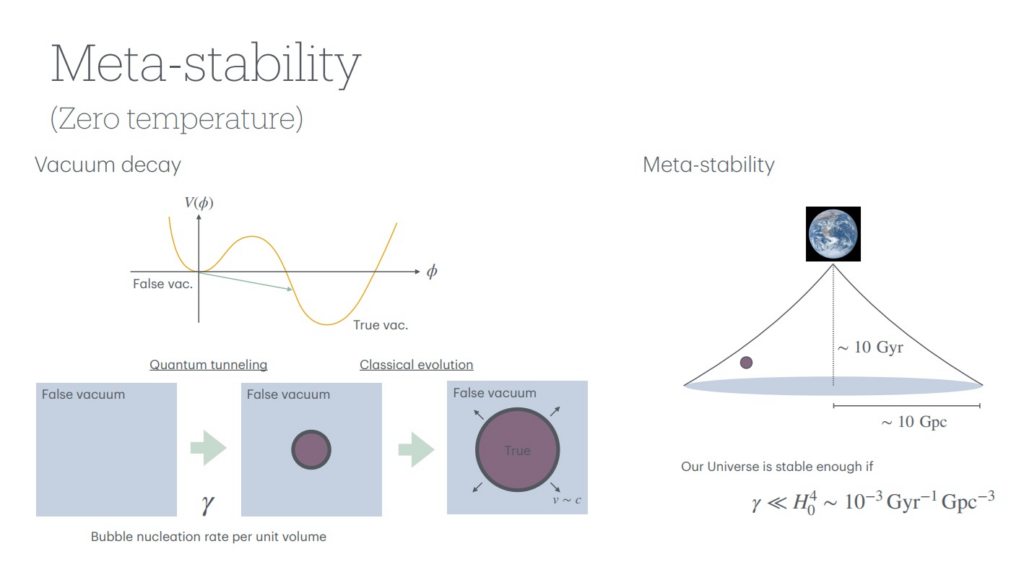
宇宙の相転移を紐解く手助けとして
直感的に使えて非常に多くの良質な関数が含まれているのが魅力です。日々の計算ノートとして役に立っています。(ヨジェフ・シュテファン研究所)
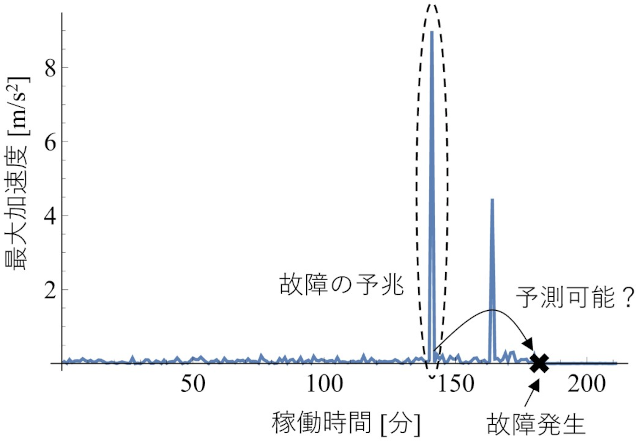
信頼性工学での導入:Mathematicaを活用した故障予測
確率分布の実装だけでなく信頼性解析等、工学的解析の関数も充実しており、大変重宝しています。さらにネットワークモデルの構築や学習処理も短いプログラムで手軽に実行でき、助かっています。(神奈川大学工学部)
次世代電子陽電子衝突器の研究
素粒子物理学の研究及び教育において、Symbolic Manipulation と数値計算、図や 3D 表示、動画の作成などで Mathematica が活躍しています。(東北大学/バレンシア大学)
授業教材の作成から分析や研究まで,Mathematica でできるたくさんの事
C 言語/Python だと必要になるアプリの設定、コンパイラなどの環境構築も Mathematica ではとても楽なので、ちょっとしたプログラムの受け渡しもとてもスムーズです。(国立大学法人富山大学)
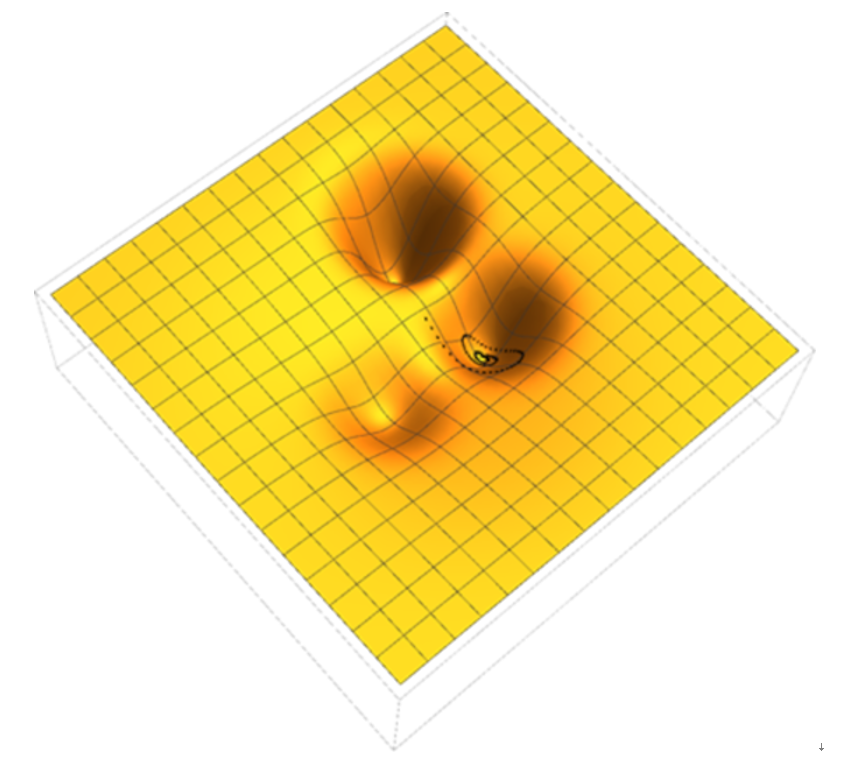
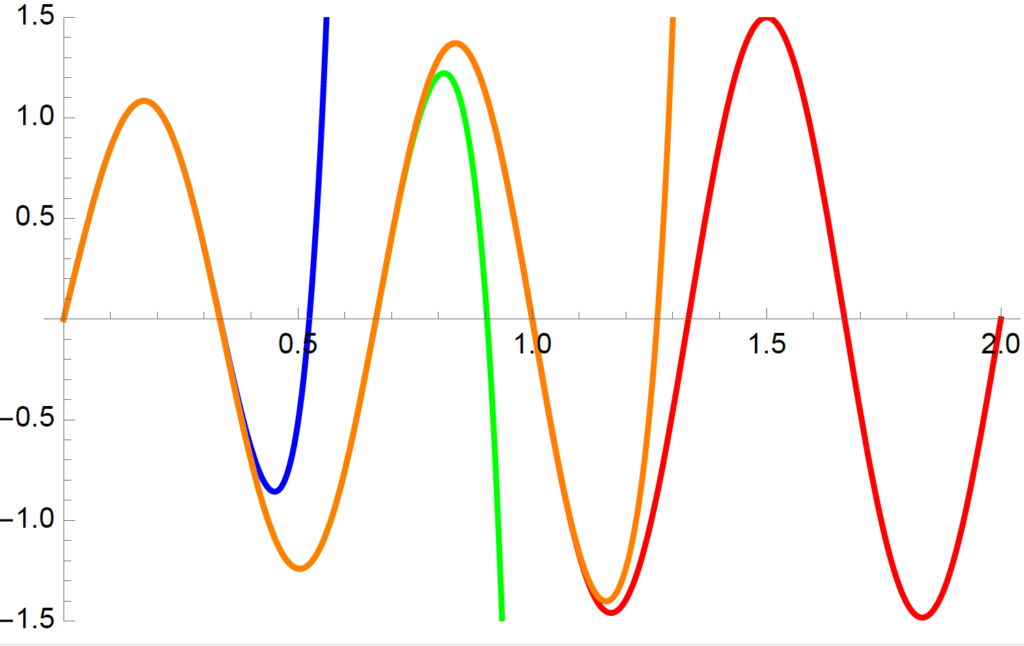
数式処理のアルゴリズム・応用研究と数学科の計算機演習への活用
プログラミングや計算の場面では 最新アルゴリズムを含む先進性と汎用性、プログラム開発や計算機教育の場面では 用途に応じた効果的な手法選択、容易に対話的UI構築可能な柔軟性、等の多くの魅力があります。(筑波大学)
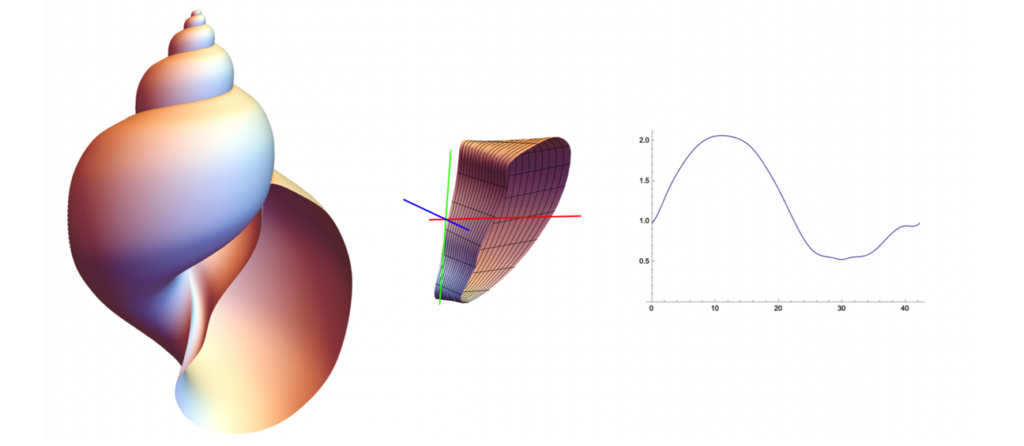
生物の「かたち」の定量解析への活用
多種多様なデータフォーマットをサポートしており、多様な解析に使える豊富な関数と、統一されたインターフェース・解析環境により 2 次元、3 次元での可視化もシームレスにおこなえる点が魅力です。(九州大学大学院)
大学で広く数学に関わる知的活動支援に活用
学生の学習支援環境として Mathematica や Wolfram|Alpha を、数学基礎・応用教育の他 ラーニングコモンズ等でも活用しています。「自分で考える時にヒントになる」よう設計されており、初めて知った学生のほとんどは「もっと早く知りたかった」といいます。 (同志社大学)
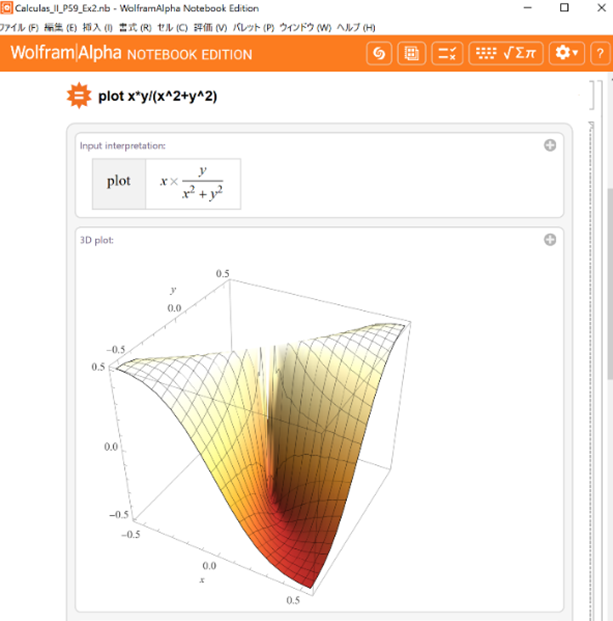
SystemModeler で記述したシステムの計算を Mathematica で解析
モデルベース開発のためのモデリング手法やシミュレーション手法、特にこれらの手法に基づくシステム設計支援手法を研究していく中で、運動や熱、制御など様々なドメインで構成される複雑なシステムの記述環境として SystemModeler を使用し、そこから得られる計算結果の解析に Mathematica を使用しています。 (国立研究開発法人産業技術総合研究所・製造技術研究部門)
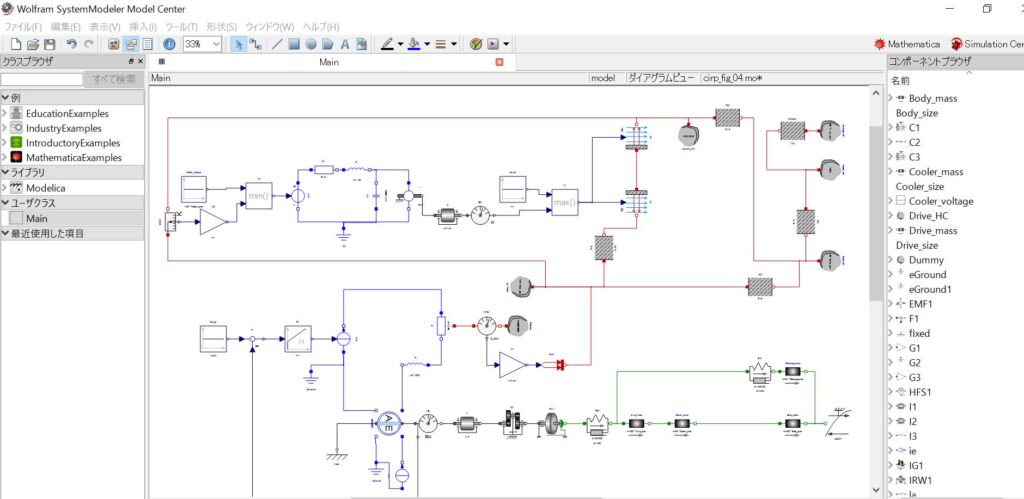
明治大学・総合数理学部・現象数理学科で Mathematica を導入
2013 年 4 月に明治大学 中野キャンパスに開設された総合数理学部 現象数理学科では、数理解析、コンピュータ、モデリングを柱として複雑現象の解明をめざし、Mathematica の導入されたコンピュータを用いて数学を実体験できる授業を行っています。 (明治大学・総合数理学部・現象数理学科)
光学分野におけるWolfram Mathematicaの活用
複雑な光学現象の解析やシステム設計には、高度な計算能力が不可欠です。
Mathematicaは強力な数式処理、数値計算、多彩な可視化、そして柔軟なプログラミング環境をシームレスに統合し、 光学系のモデリングから設計、データ解析に至るまで、アイデアを迅速に形にし、深い洞察を得るための最適なプラットフォームを提供します。