19.4 マン=ホイトニーの順位和検定

順位和検定 (Rank Sum Test) を使うのは：

• 異なる２つの標本の中央値 (median) の間に有意な差があるかどうかを調べたいとき。
• 分散の等しい正規分布母集団から標本が抽出されていないとき、または、正規母集団から標本が抽出されていることを前提条件にしたくないとき。

抽出したデータの母集団に正規性があることが分かっている場合は、対応のない t 検定 (Unpaired t-test) を使います。詳しくは、対応のない t 検定 をご覧ください。比較する群が２つ以上ある場合は、Kruskal-Wallis の順位に基づく分散分析 (Kruskal-Wallis ANOVA on Ranks test) を実行します。詳しくは、クラスカル=ウォリスの順位に基づく分散分析 をご覧ください。

※ Note：Rank Sum Test のオプション設定によっては、順位和検定を正規母集団に対して実行しようとする際、そのデータを順位和検定よりパワフルな対応のない t 検定 (Unpaired t-test) で分析できることが SigmaPlot により告知されます。

1. マン=ホイトニーの順位和検定について
2. マン=ホイトニーの順位和検定を実行する
3. 順位和のデータを配置する
4. マン=ホイトニーの順位和検定オプションを設定する
   1. Options for Rank Sum Test: Assumption Checking
   2. Options for Rank Sum Test: Results
5. 順位和検定を実行する
6. 順位和検定の結果を解釈する
   1. 結果の説明
7. 順位和検定のレポートグラフ
   1. 順位和検定のレポートグラフを作成する方法

 

1. マン=ホイトニーの順位和検定について

２群の間に無作為なサンプリングによる変動から生じる差よりも大きな差があるか否かを検定するには、マン=ホイトニーの順位和検定 (Mann-Whitney Rank Sum Test) を使います。帰無仮説は「２つの標本は異なる中央値 (median) の母集団から抽出されたものではない」です。

順位和検定 (Rank Sum Test) は、前提条件に正規性や等分散性を必要としないノンパラメトリックな検定法です。観測されたデータがいずれの群から抽出されたものであるかにかかわらず、観測された全てのデータについて、その最小から最大までに順位を付けます。付けられた順位は、各群ごとに合計し、その順位和を比較します。

２群の間に差がなければ、それぞれの順位の平均値 (mean rank) は殆ど同じになります。これらの間に大きな差があるとすれば、片方の群が順位の低いものになる傾向があり、もう片方の群が順位の高いものになると見なすことができるので、２つの標本は異なる母集団から抽出されたものである (例えば、統計的に有意な差がある) と結論付けることができます。

 

2. マン=ホイトニーの順位和検定を実行する

マン=ホイトニーの順位和検定 (Mann-Whitney Rank Sum Test) を実行するには：

1. ワークシートに適切なデータを入力または配置します。詳しくは、順位和のデータを配置する をご覧ください。
   
   
2. 必要があれば、Rank Sum オプションを設定します。
   
   
3. Analysis タブをクリックします。
   
   
4. SigmaStat グループにある Tests ドロップダウンリストから以下を選択します：
   
   Compare Two Groups → Rank Sum Test
   
   
5. 検定を実行 (Run) します。
   
   
6. レポートグラフを作成します。詳しくは、順位和検定のレポートグラフ をご覧ください。

 

3. 順位和のデータを配置する

検定に使用するデータフォーマットには、生データ (raw data) またはインデックス付きデータ (indexed data) を利用できます。いずれの場合も、ワークシートの２列を使います。

マン=ホイトニーの順位和検定で有効なデータフォーマットの例。

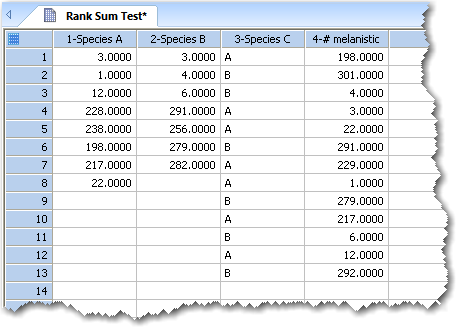列１と２には、生データ (raw data) を配置しています。列３と４には、列３を因子列とする群別のインデックス付きデータを配置しています。

 

4. マン=ホイトニーの順位和検定オプションを設定する

1. Analysis タブの SigmaStat グループにある Select Test ドロップダウンリストから Rank Sum Test を選択します。
   
   
2. 現在の検定の Options をクリックします。 Options for Rank Sum Test ダイアログボックスに以下の２つのタブが表示されます：
   
   
   1. Assumption Checking：データの正規性と等分散性の基準を緩和または厳格にするには、このパラメータを調整します。詳しくは、Options for Rank Sum Test: Assumption Checking をご覧ください。
      
      
   2. Results：データの統計サマリーをレポートに表示するか否かを指定します。Yates Correction Factor (イェーツの修正因子) を有効にする場合もこのタブを使用します。詳しくは、Options for Rank Sum Test: Results をご覧ください。

※ Tip：検定オプションを変更したあと検定を実行するにあたり、検定の実行前にデータを選択しておきたい場合は、使用するデータをポインターでドラッグします。

 

4.1 Options for Rank Sum Test: Assumption Checking

正規性 (Normality) の前提条件の検定では、母集団が正規分布に従っているかをチェックします。等分散 (Equal Variance) の前提条件の検定では、各群の平均値の周りのばらつきをチェックします。

Options for Rank Sum Test ダイアログボックスの Assumption Checking オプションの表示例。

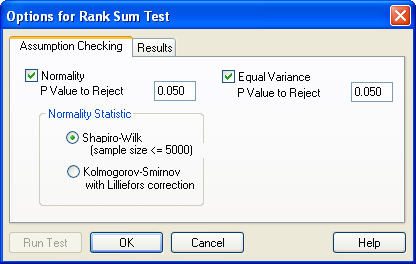• Normality の検定：SigmaPlot では、母集団の分布の正規性検定に Shapiro-Wilk または Kolmogorov-Smirnov のいずれかを使用します。
  
  
• Equal Variance の検定：SigmaPlot では、群平均のばらつきをチェックすることで等分散性を検定します。
  
  
• 正規性および等分散の P 値：P 値により、データが正規分布していないと誤って結論付ける確率が決定されます (P 値は、データが正規分布しているという帰無仮説を誤って棄却してしまうリスクです)。検定によって求められた P 値が、ここで設定した P 値よりも大きければ、帰無仮説が採択 (Pass) されます。
  
  正規性と等分散のいずれかまたは両方の要件をより厳密なものにするには、この P 値を大きくします。パラメトリックな統計手法では、仮説の棄却が比較的ロバスト (頑健) に検出されることから、SigmaPlot ではこの値を 0.050 としています。P 値をこれよりも大きくすると (例えば、0.100)、そのデータに正規性がないとの判定が出やすくなります。
  
  正規性の要件を緩和するには、P 値を小さくします。正規性があるという仮説を棄却するための P 値に小さい値しか要求しないということは、前提とする正規分布からデータが外れていても、それが非正規であると判定される前に、それだけ広く受け入れたいとする意思があることを意味します。例えば、P 値を 0.010 とした場合、あるデータを非正規であると判定するには、0.050 の場合と比べてそれだけ大きく正規性を逸脱していなければなりません。

※ 制限事項

データの分布が極端な状態にあり、これらの手法では検定できない場合があります。たとえば、ルビーンの中央値検定 (Levene Median test) では、分散の大きさが数次の場合は差の検出ができません。このような条件の場合は、前提条件の自動検定に頼らずにデータを視覚的に調べることで容易に見分けることができます。

 

4.2 Options for Rank Sum Test: Results

• Summary Table：列または群の観測数 (N)、列または群の欠損値の数 (Missing)、列または群の中央値 (Median)、25% および 75% パーセンタイルを表示します。

Options for Rank Sum Test ダイアログボックスの Summary Table オプション例。

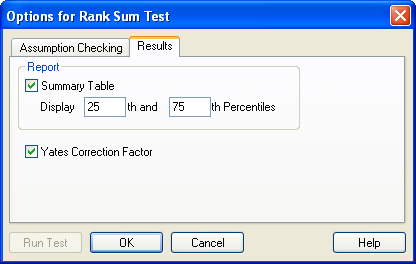• Yates Correction Factor (イェーツの修正因子) ：統計的検定で、例えば、2 x 2 分割表やマクニマー (McNemar) の検定のような、自由度１の χ² 分布を使用する場合、算出される χ² 統計量は、実際の χ² 検定統計量の分布と比べて生成される P 値が非常に小さくなる傾向があります。理論上 χ² 分布は連続型ですが、この検定の χ² 分布は離散型です。イェーツの修正因子 (Yates Correction Factor) を使えば、算出される χ² 値を調整して、このずれを補うことができます。イェーツの修正因子を使うことで検定の取扱いが慎重になります：例えば、P 値が増加するので偽陽性を結論付ける可能性が少なくなります。イェーツの修正は、2 x 2 分割表や、自由度１の χ² 分布から P 値を算出するその他の統計に適用します。イェーツの修正の導出に関する詳しい説明については、統計学の参考書をご覧ください。

 

5. 順位和検定を実行する

検定を実行する前にお持ちのデータを選択しておきたい場合は、対象となるデータをマウスポインタでドラッグしておきます。

1. Analysis タブをクリックします。
   
   
2. SigmaStat グループにある Tests ドロップダウンリストから次を選択します：
   
   Compare Two Groups → Rank Sum Test
   
   検定ウィザードの Data Format パネルで、データフォーマットを選択します。
   

   Rank Sum Test — Data Format ダイアログボックスで Data Format を指定 。

   
   
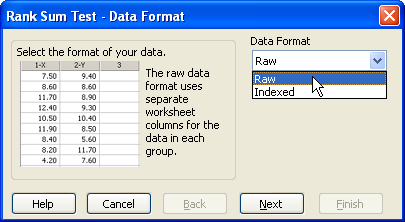3. Data Format ドロップダウンリストから該当するデータフォーマットを選択します。詳しくは、群比較検定のデータフォーマット をご覧ください。
   
   
4. Next をクリックして、検定するデータ列を選択します。この検定を選択する前に列を選択していれば、Selected Columns リストに選択した列が表示されます。
   

   Rank Sum Test — Select Data ダイアログボックスでデータ列を選択。

   
   
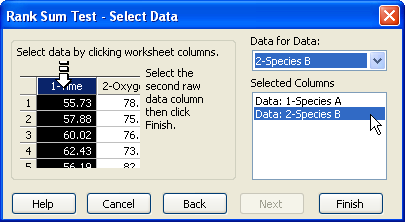5. Selected Columns リストに別のワークシート列を割り当てたい場合には、ワークシートで直接その列を選択するか、Data for Data ドロップダウンリストからその列を選択します。
   
   Selected Columns リストの一行目に割り当てられるのは最初に選択した列で、以後同様に列を選択するごとにリストの２行目以降に割り当てられてゆきます。各行には、選択した列のタイトルが表示されます。生データ (Raw) とインデックス付きデータ (Indexed) の場合は、ワークシートの２列を選択するよう指示されます。
   
   
6. 選択した内容を変更するには、リストの割り当てを選択したあと、ワークシートから列を選択しなおします。Selected Columns リストの内容をダブルクリックすることによって、列の割り当てを消去することもできます。
   
   
7. Finish をクリックすると、選択した列にもとづく Rank Sum Test (順位和検定) が実行されます。
   
   正規性と等分散性を検定するよう選択した場合、SigmaPlot により、正規性の検定 (Shapiro-Wilk または Kolmogorov-Smirnov) と等分散性の検定 (Levene Median) が実行されます。お持ちのデータがいずれの検定にも合格した場合、SigmaPlot により、その結果が報告され、対応のない t 検定を用いて分析を続行するよう提案されます。詳しくは、対応のない t 検定 をご覧ください。
   
   計算が完了すると、レポートが表示されます。

 

6. 順位和検定の結果を解釈する

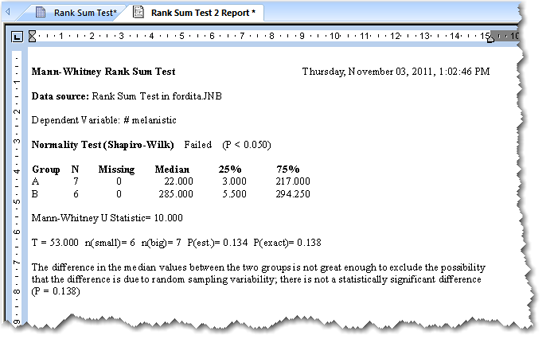
この順位和検定では、マン=ホイトニーの T 統計量 (Mann-Whitney T statistic) とその T に関する P 値が計算されます。これらの結果は、順位和検定の実行後に表示される Rank Sum Test レポートに表示されます。レポートに表示されるその他の結果は、Options for Rank Sum Test ダイアログボックスで有効または無効にすることができます。

 

6.1 結果の説明

数値による結果に加えて、拡張された結果の説明が表示されることがあります。この説明テキストは、Options ダイアログボックスで有効または無効にすることができます。

• Normality Test：Normality Test の結果には、そのデータが正規母集団から抽出されたものであるという前提条件の検定に合格したか否か (Passed または Failed)、および、この検定で計算された P 値が表示されます。ノンパラメトリックの検定法では、母集団の正規分布を前提条件としないのでこの検定には合格しません (Failed になります)。この結果は、Options for Rank Sum Test ダイアログボックスで設定します。
  
  
• Equal Variance Test：等分散性の検定 (Equal Variance test) の結果には、そのデータが同じばらつきを持つ母集団から抽出されたものであるという前提条件の検定に合格したか否か (Passed または Failed)、および、この検定で計算された P 値が表示されます。ノンパラメトリックの検定法では、母集団の等分散性を前提条件としません。この結果は、Options for Rank Sum Test ダイアログボックスで設定します。
  
  
• Summary Table：SigmaPlot では、サンプルサイズ N、欠損値の数 (Missing)、中央値 (Median)、および、２つのパーセンタイルを一覧にしたサマリーテーブルが作成されます。この結果は、Options for Rank Sum Test ダイアログボックスの Summary Table オプションを無効にしない限り表示されます。
  
  
  • N (Size)：該当する列または群の観測値の数です。
    
    
  • Missing：該当する列または群の欠損値の数です。
    
    
  • Medians：全ての観測値を小さい順に並べて、観測値の小さい方の半数の中からの最大値を選択することで算出する観測値の「中央」です。観測した中央値では、その観測値よりも大きい観測数と小さい観測数が同じになります。
    
    
  • パーセンタイル：観測値の上側と下側の両端を定義した２つのパーセンタイル点です。
    
    
  • T 統計量：T 統計量は、小さい方の標本群、または、両群のサイズが同じ場合は最初に選択した群の順位の合計です。この値を、全ての可能な順位の母集団と比較して、この T が発生する確率を決定します。
    
    
  • P 値：P 値は、2群の間に真の差があると誤って結論付けてしまう確率です (例えば、T に基づいて帰無仮説を誤って棄却する確率、すなわち、第一種の誤り (Type I error) です)。P 値が小さいほど、異なる母集団から標本が抽出される確率が高くなります。
    
    伝統的には、P < 0.05 の場合は、有意差があると結論付けることができます。

 

7. 順位和検定のレポートグラフ

順位和検定の結果を利用して、以下に示す最大２つのグラフを作成できます：

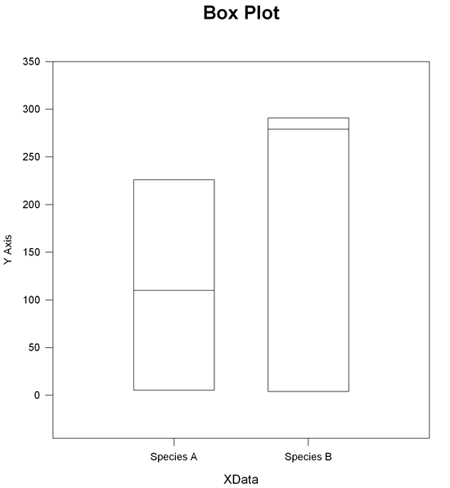
• 列データのパーセンタイルと中央値の箱ひげ図 (Box plot of the percentiles and median of column data)：順位和検定のボックスプロットでは、列データのパーセンタイルと中央値がプロットされます。その両端が 25% 点と 75% 点で定義されるボックスには、中央値をあらわす一本のライン、および、10% 点と 90% 点で定義されるエラーバーが追加されます。詳しくは、Box Plot をご覧ください。
  
  
• 列データのポイントプロット (Point plot of the column data)：順位和検定のポイントプロットでは、列ごとの全ての値がグラフ上の点としてプロットされます。詳しくは、Point Plot をご覧ください。

 

7.1 順位和検定のレポートグラフを作成する方法

1. Rank Sum Test のレポートを選択します。
   
   
2. Report タブをクリックします。
   
   
3. Results Graphs グループにある Create Result Graph をクリックします。
   
   Create Result Graph ダイアログボックスが表示され、その中に Rank Sum Test の結果で利用できるグラフのタイプが表示されます。
   

   Rank Sum Test Report の Create Result Graph ダイアログボックス

   
   
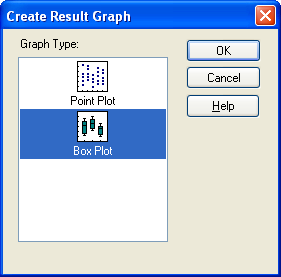4. Graph Type リストの中から作成したいグラフタイプを選択して OK をクリックするか、リスト内のグラフをダブルクリックします。
   
   選択したグラフがグラフウィンドウに表示されます。詳しくは、レポートグラフ をご覧ください。

Rank Sum Test の結果のデータをあらわす箱ひげ図