回帰曲線の目的
回帰分析とも呼ばれる回帰曲線は、一連のデータポイントに「最適」な直線または曲線を特定するために使用します。ほとんどの場合、回帰曲線は曲線上の任意の点を算出するために使用可能な数式を生成します。一部、数式の特定を考慮しない場合もあります。また、データを滑らかにしてプロットの外観を改善する目的に回帰曲線を使用する場合もあります。KaleidaGraph には、これらの両方のシナリオに使用可能な回帰曲線が備えられています。
回帰曲線のタイプ
KaleidaGraph がサポートしている回帰曲線は、最小二乗回帰曲線、非線形回帰曲線、スムース回帰曲線の 3つのカテゴリに大分することができます。ここでは、各カテゴリについて説明します。
- 最小二乗回帰曲線
 最小二乗法は、長い間一般的に使用されてきた回帰曲線の方法です。最小二乗法では、オリジナルのデータと方程式が予想した数値の間のエラーの二乗を最小化します。この方法は、関数をデータセットに適合する上で最も統計的にローバストな方法ではないかもしれませんが、(必要なコンピュータパワーの点で)比較的単純で、わかりやすいという利点があります。 最小二乗法は、長い間一般的に使用されてきた回帰曲線の方法です。最小二乗法では、オリジナルのデータと方程式が予想した数値の間のエラーの二乗を最小化します。この方法は、関数をデータセットに適合する上で最も統計的にローバストな方法ではないかもしれませんが、(必要なコンピュータパワーの点で)比較的単純で、わかりやすいという利点があります。
- 最小二乗法の欠点はデータの外れ値によって影響を受けやすい点にあります。あるデータポイントが大部分のデータと大幅に異なっていると、回帰結果が歪曲してしまいます。このため、適合の前に必ずデータを検証する必要があります。KaleidaGraph のデータ選択ツールを使用することで、図を見て簡単にプロットから外れ値を削除することができます。
- KaleidaGraph では、線形、多項式、指数、対数、および累乗の 5種類の最小二乗回帰曲線を提供しています。
- 非線形回帰曲線
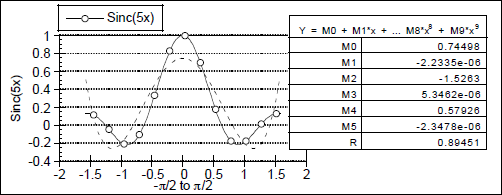
KaleidaGraph では、一般回帰曲線を通じて非線形回帰曲線をサポートしています。この機能を使用して、独自の方程式を定義したり、100 種類を超える回帰曲線の定義のライブラリから選択することができます。ほとんどすべての方程式をデータに指定できるので、KaleidaGraph の最も強力な回帰曲線オプションです。
- 一般回帰曲線は Levenberg-Marquardt アルゴリズムに基づいていて、反復法を使用して計算されます。KaleidaGraph では、最初に数式に提供された未知のパラメータを推定します。次に、オリジナルデータと計算結果の間の 2乗誤差の和を示すカイ2乗値を計算します。各反復作業の間、KaleidaGraph ではパラメータ値をわずかに変更し、最適な結果が得られるまでカイ 2乗値を再評価します。
- スムース回帰曲線
KaleidaGraph のスムース曲線は、その他の 2種類の曲線と異なり、生成する曲線の方程式を生成しません。これは、この曲線を表すことができる単一の方程式が存在しないためです。これらの回帰曲線は、データに対してスムースな曲線を描画してプロットの外観を改善したい場合に使用します。
- KaleidaGraph では、スムース、加重、3次元スプライン、および補間の 4種類のスムース回帰曲線を提供しています。これらの回帰曲線はそれぞれ異なる方法で最終的な曲線を算出するので、複数の回帰曲線を試してみることをお勧めします。
- スムース回帰曲線と補間回帰曲線は同じ基本テクニックに基づいていますが、スムース回帰曲線では幾何学的な重みを組み込んで最終的な曲線を算出しています。加重回帰曲線では、部分的に加重した最小二乗エラー (Lowess) 法が使用されます。3次元スプライン回帰曲線では、一連の 3次多項式を使用して計算します。
回帰曲線モデルの選択
KaleidaGraph には、さまざまな種類の回帰曲線と 100 種類を超える一般回帰曲線の式が備えられているので、特定のデータに適した回帰曲線モデルを選択することは容易ではありません。回帰曲線モデルを選択する際は、データに関する基本的な性質を知っておくと使用するモデルを選択する上で役に立ちます。
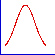
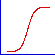
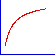
| 回帰曲線のさまざまな形状 |
 |
 |
 |
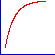 |
| ピーク |
シグモイド |
双曲線 |
指数増加 |
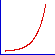 |
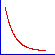 |
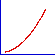 |
 |
| 数成長 |
指数減衰 |
べき乗 |
波形 |
|
- 研究分野に応じて、特定の数式が使用される場合があります。たとえば、酵素反応速度論の分野では、用量反応データにはシグモイド曲線が使用され、リガンド結合データには双曲線関数が使用されるのが一般的です。
- どのタイプの回帰曲線を使用するべきか判らない場合は、同僚に相談するか、収集したデータのタイプに通常使用される回帰曲線について調査してみてください。それでも判らない場合やデータについて何も知られていない場合は、モデルの選択は元データに基づいて行なう必要があります。
- 散布図プロットを使用しデータをプロットして、曲線の大まかな形状を確認できます。上の図では、KaleidaGraph で使用されている一般回帰曲線のなかでも比較的一般的な曲線の形状を紹介します。それぞれの形状ついて、KaleidaGraph にはさまざまな回帰曲線の数式が用意されているので、最適な結果を示す式を見つけることができます。
回帰曲線の適用
- 最小二乗法の適用
- 線形曲線の当てはめ
- 多項式曲線の当てはめ
- 指数曲線の当てはめ
- 対数曲線の当てはめ
- 累乗曲線の当てはめ
- スムースの適用
- スムース曲線の当てはめ
- 加重曲線の当てはめ
- 3次元スプライン曲線の当てはめ
- 補間曲線の当てはめ
- 線形曲線を当てはめるには:
| 関数:Y=m0+m1*x |
| 解説:この関数は上記の形式の直線をデータに当てはめます。この回帰分析についてはデータの制限がありません。 |
| 注意:半対数あるいは対数-対数の軸では、この分析は曲線で表示されます。 |
- 回帰曲線>線形 を選択して、回帰曲線の選択ダイアログを表示します。列の名前の下に従属変数がすべて表示されます。
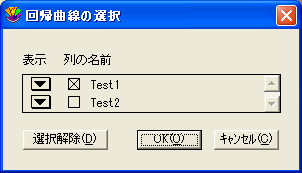
- 当てはめる変数のチェックボックスをオンにします。
- Ctrl+A(Windows)、Command+A(Macintosh)キーを押すと、すべての変数が選択されます。
- OK をクリックするとプロットウィンドウに戻り、選択した変数に曲線が当てはめられます。
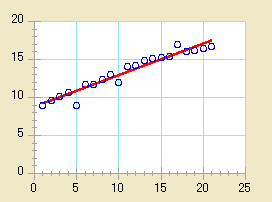 |
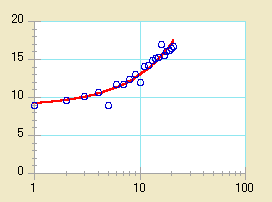 |
| x 軸が線形の場合 |
x 軸が対数の場合 |
関連:クイックスタートガイド「回帰曲線のあてはめ」
- 多項式曲線を当てはめるには:
| 関数:Y=m0+m1*x+m2*x2+m3*x3+...+m9*x9 |
| 解説:この関数は上記の形式の曲線をデータに当てはめます。データの曲率が複雑になると、それを当てはめるのに必要な多項式の次数が高くなります。この回帰分析についてはデータの制限がありません。 |
- 回帰曲線>多項式を選択して、回帰曲線の選択ダイアログを表示します。列の名前の下に従属変数がすべて表示されます。
- 当てはめる変数のチェックボックスをオンにします。
- Ctrl+A(Windows)、Command+A(Macintosh)キーを押すと、すべての変数が選択されます。
- 変数を選択するたびに、2番目のダイアログが表示されます。このダイアログから、当てはめる多項式の次数を指定します。
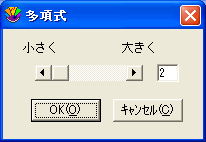
- 両方のダイアログの OK をクリックしてプロットウィンドウに戻ります。選択した変数に多項式曲線が当てはめられます。
| 注意: 当てはめる曲線の変数を選択するときに Shift キーを押すと、各変数について現在の多項式の次数が使用されます。この方法を使用して、次数を一度設定し、残りの変数の次数を2番目のダイアログを表示せずに設定することができます。 |
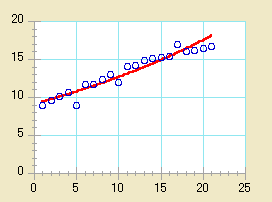
- 指数曲線を当てはめるには:
| 関数:Y=m0*exp(m1*x) |
| 解説:この関数は上記の形式の曲線をデータに当てはめます。これは高い割合で増減するデータに適しています。この回帰分析は負のデータや 0 に等しいデータには適しません。 |
| 注意:半対数軸では、曲線は直線で表示されます。 |
- 回帰曲線>指数を選択して、回帰曲線の選択ダイアログを表示します。列の名前の下に従属変数がすべて表示されます。
- 当てはめる変数のチェックボックスをオンにします。
- Ctrl+A(Windows)、Command+A(Macintosh)キーを押すと、すべての変数が選択されます。
- 両方のダイアログの OK をクリックしてプロットウィンドウに戻ります。選択した変数について指数曲線が当てはめられます。
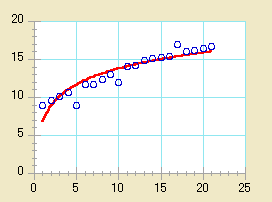
- 対数曲線を当てはめるには:
| 関数:Y=m0+m1*log(x) |
| 解説:この関数は上記の形式の曲線をデータに当てはめます。対数回帰分析は一般に 10 のべき乗単位で推移するデータ (10^0、10^1、10^2、等など) に使用されます。この回帰分析は負のデータや 0 に等しいデータには適しません。 |
| 注意:線形 Y 軸の半対数プロットでは、曲線は直線で表示されます。 |
- 回帰曲線>対数を選択して、回帰曲線の選択ダイアログを表示します。列の名前の下に従属変数がすべて表示されます。
- 当てはめる変数のチェックボックスをオンにします。
- Ctrl+A(Windows)、Command+A(Macintosh)キーを押すと、すべての変数が選択されます。
- OK をクリックしてプロットウィンドウに戻ります。選択した変数について対数曲線が当てはめられます。
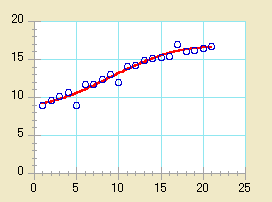
- 累乗曲線を当てはめるには:
| 関数:Y=m0*x^m1 |
| 解説:この関数は上記の形式の曲線をデータに当てはめます。この回帰分析は負のデータや 0 に等しいデータを当てはめるのには使用できません。 |
| 注意:対数-対数軸では、曲線が直線になります。 |
- 回帰曲線>累乗を選択して、回帰曲線の選択ダイアログを表示します。列の名前の下に従属変数がすべて表示されます。
- 当てはめる変数のチェックボックスをオンにします。Ctrl+A(Windows)、Command+A(Macintosh)キーを押すと、すべての変数が選択されます。
- OK をクリックしてプロットウィンドウに戻ります。選択した変数について対数曲線が当てはめられます。
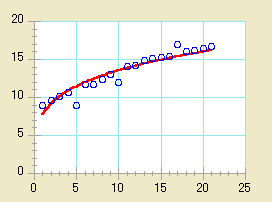
- スムース曲線を当てはめるには:
| この関数はデータにスムースな曲線を当てはめます。KaleidaGraph はデータに Stineman 関数を適用します。この関数の出力はスムースな曲線を実現するために、幾何学的なウェイトを現在のポイントに適用し、±10% のデータ範囲を持っています。 |
| この回帰分析に関連する唯一のデータ制限は、独立 (X) 変数がデータウィンドウに昇順で並んでいなければならないことです。この曲線を表す表現はひとつではありません。したがって、表示あるいはコピーするパラメータはありません。 |
- 回帰曲線>スムースを選択して、回帰曲線の選択ダイアログを表示します。列の名前の下に従属変数がすべて表示されます。
- 当てはめる変数のチェックボックスをオンにします。
- Ctrl+A(Windows)、Command+A(Macintosh)キーを押すと、すべての変数が選択されます。
- OK をクリックしてプロットウィンドウに戻ります。選択した変数についてスムース曲線が当てはめられます。
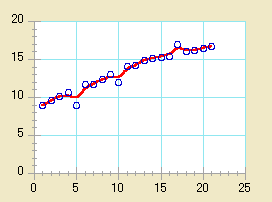
- 加重曲線を当てはめるには:
| この関数は、部分的にウェイトを置いた最小二乗法を使用して、曲線をデータに当てはめます。この回帰分析の結果はデータの中央に最適なスムース曲線をプロットします。これはかなり強力な当てはめのテクニックです。標準的な最小二乗法と違って、このテクニックは外れ値をほとんど内包するものです。しかし、これはいい加減なものではありません。加重回帰曲線は、コンピュータの計算上複雑で、データが多量の場合には非常に長い時間がかかります。 |
| この回帰分析に関連する唯一のデータ制限は、独立 (X) 変数がデータウィンドウに昇順で並んでいなければならないことです。この曲線を表す表現はひとつではありません。したがって、表示あるいはコピーするパラメータはありません。 |
- 回帰曲線>加重を選択して、回帰曲線の選択ダイアログを表示します。列の名前の下に従属変数がすべて表示されます。
- 当てはめる変数のチェックボックスをオンにします。
- Ctrl+A(Windows)、Command+A(Macintosh)キーを押すと、すべての変数が選択されます。
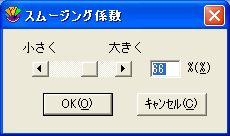
- 変数を選択するたびに、2番目のダイアログが表示されます。このダイアログでは、スムージング時に考慮される、データ全体に対する部分データを処理するスムージング係数を変更することができます。この値を大きくするほど、個々のデータが最終的な曲線形状に与える影響が小さくなります。典型的な値の範囲は 33~66 です。最小値は 0、最大値は 100 です。
- 両方のダイアログの OK をクリックして、プロットウィンドウに戻ります。選択した変数について加重曲線が当てはめられます。
| 注意: 変数を選択するときに Shift キーを押すと、現在のスムージング係数が各変数に使用されます。この方法を使用して、一度係数を選択した後は残りの変数について 2番目のダイアログを表示せずにスムージング係数を設定することができます。Ctrl+.(ピリオド)(Windows)、Command+. (ピリオド) (Macintosh) キーを押すと、いつでも加重曲線の当てはめがキャンセルされます。 |
- 3次元スプライン曲線を当てはめるには:
| X の増加に伴って曲線の左から右に移動するので、4つの連続するデータの各グループは 3次の多項方程式を定義します。結合したこれらの 3次多項式は 3次元スプライン曲線を定義します。この回帰曲線を使うと、全てのデータポイントに結びついた雲形定規を使用した場合と似たものになります。 |
| この回帰分析に関連する唯一のデータ制限は、独立 (X) 変数がデータウィンドウに昇順で並んでいなければならないことです。この曲線を表す表現はひとつではありません。したがって、表示あるいはコピーするパラメータはありません。 |
- 回帰曲線>3次元スプラインを選択して、回帰曲線の選択ダイアログを表示します。列の名前の下に従属変数がすべて表示されます。
- 当てはめる変数のチェックボックスをオンにします。
- Ctrl+A(Windows)、Command+A(Macintosh)キーを押すと、すべての変数が選択されます。
- OK をクリックしてプロットウィンドウに戻ります。選択した変数について 3次元スプライン曲線が当てはめられます。
 |
 |
| |
拡大した場合 |
- 補間曲線を当てはめるには:
| この関数はデータポイントを通り、それらのポイントのスロープにマッチする曲線を当てはめます。この曲線の利点は、3次元スプライン回帰曲線で発生するような突然のスロープの変化に近似した乱暴な結果を生み出さないことです。 |
| この回帰分析に関連する唯一のデータ制限は、独立 (X) 変数がデータウィンドウに昇順で並んでいなければならないことです。この曲線を表す表現はひとつではありません。したがって、表示あるいはコピーするパラメータはありません。 |
- 回帰曲線>補間を選択して、回帰曲線の選択ダイアログを表示します。列の名前の下に従属変数がすべて表示されます。
- 当てはめる変数のチェックボックスをオンにします。
- Ctrl+A(Windows)、Command+A(Macintosh)キーを押すと、すべての変数が選択されます。
- OK をクリックしてプロットウィンドウに戻ります。選択した変数について補間曲線が当てはめられます。
 |
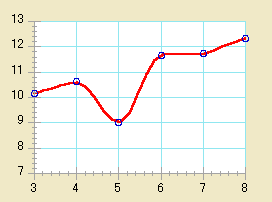 |
| |
拡大した場合 |
一般回帰曲線の基礎
回帰曲線の定義
回帰曲線の定義とは、データに当てはめる方程式を指します。回帰曲線の定義は、数式入力で用いる演算子、変数、関数、常数と、さらに独立変数で構成されます。
式中の独立変数は、m0 で表現されます。パラメータは、m1~ m9 が計算に使われます。パラメータは未知数を表しており、カレイダグラフがその最善の値を計算します。
回帰曲線を定義するために、ライブラリに常数とその他のリファレンスが書かれてあります。デフォルトライブラリでは、m0 の代わりに x を、m1、m2、m3、m4 の代わりに a、b、c、d を使っているものもあります。
回帰曲線の定義に列の番号を含めるには、table 関数を使います。この方法を使うと、独立多変数を含む方程式を当てはめることも可能です。
カレイダグラフの定義ではどのように表現されるか、例をあげます。
| 元の方程式 |
回帰曲線の定義 |
| a*x+b |
m1*m0+m2 |
| a+b*x^c |
m1+m2*m0^m3 |
| a+b*exp(-c*x) |
m1+m2*exp(-m3*m0) |
| a*exp(-b*x)*cos(c*x+d) |
m1*exp(-m2*m0)*cos(m3*m0+m4) |
|
初期条件
カレイダグラフが未知数を計算してくれるとはいえ、各パラメ-タの初期値は入力しなければなりません。この計算には、十分正しいと思われる推測値を必要とします。カレイダグラフは、曲線を当てはめながら、この値をさらに調整してゆきます。
| 注意: 初期推測値から計算が始まりますが、最適な値に変更されてゆきますので、最終結果は初期のものとは異なった値になることもあります。 |
よい推測値を見つけようと必死になる必要はありません。初期条件は、あくまで推測です。いくつにしたらよいかわからないときは、初期値をゼロにせず、正しいと思われる桁数 (たとえば 0.001、1、1000 など) を入力してください。
初期条件は、回帰曲線の定義のすぐ後に記述します。定義の終わりにはセミコロンを入れてください。さらに、セミコロンで区切って初期推測値を与えます。例を下記にあげます。
| 回帰曲線の定義と初期推測値 |
| m1*m0+m2; m1=0.5; m2=23 |
| m1+m2*m0^m3; m1=-2; m2=3; m3=2 |
| m1+m2*exp(-m3*m0); m1=5; m2=1; m3=0.5 |
| m1*exp(-m2*m0)*cos(m3*m0+m4); m1=4; m2=0.7; m3=2.2; m4=15 |
|
回帰曲線の定義ダイアログ
回帰曲線の定義ダイアログでは、方程式、初期推測値、許容誤差を入力します。部分指定、加重データの指定もできます。
このダイアログには、次の二つがあります。
- 回帰曲線メニューの一般サブメニューから、回帰曲線を選んでください。回帰曲線の選択ダイアログが表れますので、定義をクリックしてください。
- 回帰曲線メニューの一般サブメニューから、一般編集を選択してください。一般回帰曲線ダイアログが表れ、回帰曲線の名前を選択して編集をクリックしてください。
回帰曲線の定義ダイアログの設定については、後述します。
- ファイル...(F)
- このボタンをクリックすると、回帰曲線の定義を読み書きするテキストエディタが表れます。定義は第1行目に書かれ、部分導関数以下の行に記述されます。
- ヘルプ... (H)
- Deg / Rad ボタン
- 結果を Degree で表すか、 Radian で表すか選択します。
- 許容誤差:(E)
- このフィールドに入力された値を参照して、カレイダグラフは反復を中止します。以下のいずれかが発生した場合に反復が中止されます。
- カイ2乗が変化しない。
- 正規のカイ2乗のパーセント変更が許容誤差より少い。
- 加重データ(W)
- チェックすると、当てはめる変数のウェイトを含むデータコラムを指定できます。これらのウェイトは標準的なエラー値を表すものです。各ウェイトは内部的に 1/((weight)^2) として使用されます。エラー値が小さいほど、内部的なウェイトは大きくなります。チェックすると、ウェイト値 1 が使われます。
- 部分指定(S)
- カレイダグラフが一般回帰曲線の反復法を計算する際に使用するアルゴリズムは、各パラメータに関して関数の部分的な導関数を計算しなければなりません。部分指定のチェックを解除すると、カレイダグラフは導関数に近似した絶対値になります。このオプションをチェックすると、ウィンドウが広がります。
このダイアログの 9 つのボタンは、部分的な導関数をボタンの上にあるテキスト編集エリアで指定できるようにします。部分的な導関数を指定する最大の利点は正確さです。回帰曲線のアルゴリズムはこれらの部分的な導関数を使用し、最良の結果を見つけるために反復計算を行った後で、移動すべき場所に割り当てます。一般に偏差が大きい場合は正確に近似できないので、部分的な導関数の方が現実的です。
部分的な導関数をいくつか選択して指定することはできますが、全てはできません。不正な導関数を指定するより、カレイダグラフに任せて近似させた方がよいでしょう。部分導関数の入力フィールドを空にしておくと、部分的な導関数に近似するようカレイダグラフに指示が送られます。
定義済み一般回帰曲線の数式
概要: 定義済み一般回帰曲線の数式
KaleidaGraph には、一般回帰曲線とともに使用できる、定義済みの数式が 100 以上用意されています。回帰曲線の定義は、次のカテゴリに分類されています。
- 酵素動力学 (Enzyme Kinetics)
- 指数減少 (Exponential Decay)
- 指数増加 (Exponential Growth)
- 指数上昇 (Exponential Rise)
- 双曲線 (Hyperbola)
- IC50/EC50
- 対数 (Logarithmic)
- ピーク (Peaks)
- 多項式 (Polynomial)
- 累乗 (Power)
- 有理式 (Rational)
- シグモイド (Sigmoidal)
- 波形 (Waveforms)
- 収穫高の増加/作付け密度 (Yield Growth/Density)
- その他の定義 (Miscellaneous Definitions)
これらの定義は、KaleidaGraph では次のフォーマットで用意されています。
- 回帰曲線の各定義は、Curve Fits フォルダ内にテキストファイルとして保存されています。
- 各カテゴリの定義は、一般サブメニューに定義を読み込み可能なマクロファイルとして保存されています。
- 各カテゴリの定義は、ライブラリで使用できるテキストファイルとして保存されています。
回帰曲線リストの管理
回帰曲線のマスターリスト
カレイダグラフは新しくプロットが作成されるたびに、一般サブメニューに表れる回帰曲線のマスターリストを保守します。このマスターリストを編集するには、新しくプロットを作って、一般編集コマンドを実行します。マスターリストは、以下の作業を行っても影響されません。
- 保存されたプロットを使う (圧縮されたデータを持つプロットを使う)。
- 一般サブメニューから回帰曲線を選び、定義を編集するため一般編集をクリックする。
マスターリストに回帰曲線を追加する
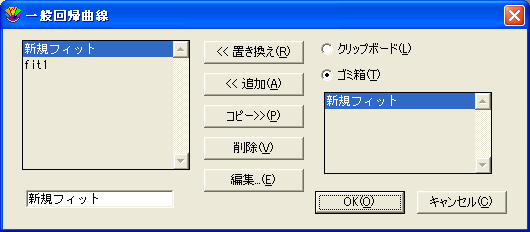
- マスターリストに回帰曲線を追加する方法:
- 新しいプロットを作ってください。
- 回帰曲線メニューの一般サブメニューから、一般編集を選択してください。
- 表示されたリストから、曲線を一つ選んでください。
- 追加をクリックすると、新規フィットがリストに表れます。それを選択し、リストの下のテキストフィールドで名前を変更することができます。
- 編集をクリックし、一般回帰曲線の定義ダイアログで曲線を定義してください。
- 終わったら、OK をクリックしてください。これで、現在開いているプロットおよび新しく作るプロットで曲線が利用できるようになりました。変更をマクロファイルに保存するのを忘れないでください。
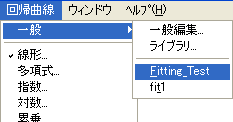
マスターリストの再配置
- マスターリストを再配置する方法:
- 新しいプロットを作ってください。
- 回帰曲線メニューの一般サブメニューから、一般編集を選択してください。
- 移動させたい回帰曲線を選択します。
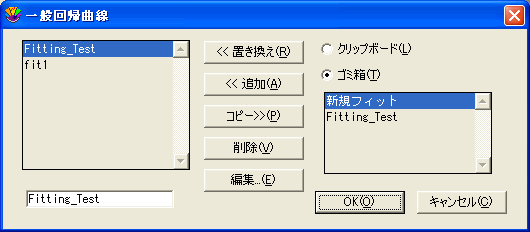
- ごみ箱にコピーするため、コピーをクリックしてください。
- リストから名前を削除するには削除をクリックします。
- リストに戻ってください。
- ゴミ箱へコピーされた回帰曲線の名前を選択します。
- 追加をクリックすると、回帰曲線がリストに配置されます。
| 注意: 回帰曲線を再配置するとき、完全に終了しない限り一般編集ダイアログを終了させないように注意してください。このダイアログの OK やキャンセルをクリックすると、ゴミ箱にある全てのものが直ちに削除されます。常にゴミ箱にある項目は新規フィットだけです。 |
マスターリストからの削除
- マスターリストから削除する方法:
- 新しくプロットを作ります。
- 回帰曲線メニューの一般サブメニューから、一般編集を選択してください。
- 削除したい回帰曲線を選択してください。
- リストから回帰曲線を削除するために、削除をクリックします。
- 一般編集ダイアログを終了するために、OK をクリックします。
マスターリストから保存されたプロットに曲線を追加
保存されたプロットを開くと、現在開かれているマスターリストに関係なく、プロットが作られたとき利用できる曲線のリストが、一般サブメニューに表れます。
- マスターリストから保存されたプロットに曲線を追加する方法:
- 保存されたプロットを開きます。
- 回帰曲線メニューの一般サブメニューから、一般編集を選択してください。 マスターリストに保存された回帰曲線が、ごみ箱のリストに点線で区別されて表示されます。
- ゴミ箱のリストから追加したい回帰曲線の名前を選択します。
- マスターリスト内の曲線をどれか選んでください。
- 追加をクリックすると、その下に新たに回帰曲線が表示されます。
- OK をクリックします。この回帰曲線は、保存されたプロットに適用することができます。
回帰曲線メニューに変更を保存
一般サブメニューで保存された回帰曲線は、デフォルト(標準設定)では KGMacros (Windows)、KG Macros (Macintosh) に保存されます。このファイルは、カレイダグラフを立ち上げるたび読み込まれます。
回帰曲線メニューでおこなった変更を保存するためには、以下のいずれかの方法でデフォルトマクロファイルに変更を保存する必要があります。
- プリファレンスダイアログでファイル設定タブをクリックして、マクロポップアップメニューから確認を選択します。KaleidaGraph の終了時に、ダイアログが表示され、起動時に開いたマクロファイルを上書きするか確認します。
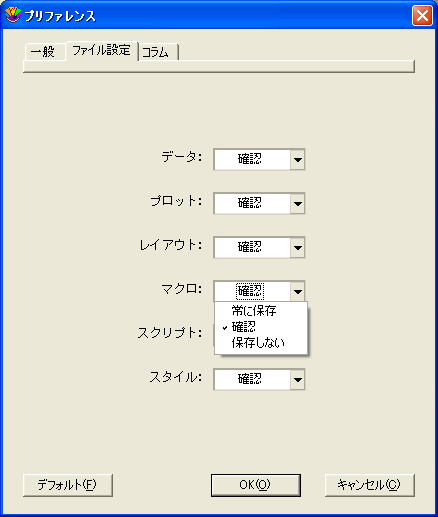
- プリファレンスダイアログでファイル設定タブをクリックして、マクロポップアップメニューから常に保存を選択します。KaleidaGraph の終了時に、起動時に開いたマクロファイルが自動的に上書きされます。
- ファイルメニューから書き出しのマクロを選択し、Default Macrosファイルを上書きしてください。
| 注意: 一般編集を使って行われた変更だけがマクロファイルの一部として保存されます。一般サブメニューや定義ボタンを使用して行った全ての変更は特定のプロットにのみ適用されます。 |
カスタム回帰曲線の使用
カスタム回帰曲線の数式の入力
定義済みの数式に含まれていない回帰曲線を使用する必要がある場合、カスタムの数式を入力してKaleidaGraphで使用することができます。
| 注意: カスタム回帰曲線の数式は、ライブラリでの定義を行うこともできます。 |
- カスタム回帰曲線の定義を作成 (して以降のすべてのプロットで使用できるように) するには:
- プロットを新規作成します。
- 回帰曲線 > 一般 > 一般編集 を選択します。
- 表示されたリストから回帰曲線を選択します。
- 追加をクリックするとリスト内の選択した回帰曲線の下に新規フィットが表示されます。新規フィットを選択してテキストフィールドで名前を編集することで、曲線の名前を変更することができます。
- 編集をクリックして、一般回帰曲線の定義ダイアログを表示します。
- 一般回帰曲線の定義ダイアログに、曲線を表す数式を入力します。未知のパラメータについて初期推測値を忘れずに指定します。回帰曲線の数式と初期推測値の例を示します。
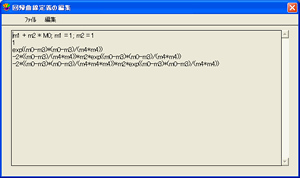
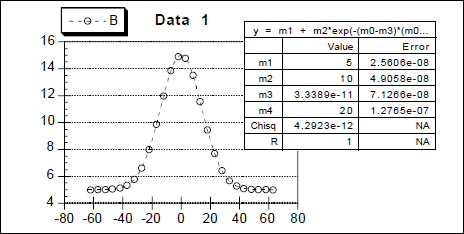
| m1+m2*exp(-(m0-m3)*(m0-m3)/(m4*m4));m1=1;m2=5;m3=1;m4=10 |
- プロットウィンドウに戻るまで繰り返し OK をクリックします。これで、現在表示されているプロット、および将来作成するプロットにこの曲線を使用することができます。変更内容を将来も使用する場合は、忘れずに変更内容をマクロファイルに保存します。
テキストファイルからの定義の読み込み
各曲線の定義は、テキストファイルとして Curve Fits フォルダにあります。特定の曲線の定義をインポートして、KaleidaGraph で使用することができます。
- 曲線の定義をもつテキストファイルをロードするには (以降のプロットに使用できるようにする):
- プロットを新規作成します。
- 回帰曲線>一般>一般編集 を選択します。
- 表示されたリストから回帰曲線を選択します。
- 追加をクリックします。リストの選択した曲線の下に新規フィットが表示されます。曲線の名前を変更するには、新規フィットを選択してテキストフィールドの名前を編集します。
- 編集ボタンをクリックして、一般曲線の定義ダイアログを表示します。
- 一般曲線の定義ダイアログのファイルをクリックして、テキストエディタを表示します。
- ファイル>開くを選択します。
- Curve Fits フォルダ内の回帰曲線の定義を開きます。テキストエディタに、パラメータの定義と初期推測値が表示されます。
- 一般曲線の定義ダイアログに回帰方程式を表示するには、ファイル>閉じるを選択します。初期推測値のデフォルト値はすべて 1.0 なので、かならず初期推測値を変更してください。
- プロットウィンドウに戻るまで OK を繰り返しクリックします。これでアクティブなプロットや新規作成するプロットにこの回帰曲線を使用できます。変更した回帰曲線を将来も使用する場合は、変更内容をマクロファイルに保存してください。
マクロファイルからの定義の読み込み
Macros フォルダには、各カテゴリの回帰曲線の定義をもつマクロファイルがあります。このマクロファイルを読み込みすると、回帰曲線の定義が一般サブメニューから使用できるようになります。
| 注意: プロットがすでに開いている場合には、プロットを新規作成するまで、読み込みした回帰曲線の定義は表示されません。 |
- マクロファイルから定義をロードするには:
- ファイル>開くを選択します。
- Macros フォルダからマクロファイルを開きます。
- プロットを新規作成します。マクロファイル内の回帰曲線の定義が、一般サブメニューの下に表示されます。
- 表示された回帰曲線をデータに当てはめることができます。初期推測値のデフォルト値はすべて 1.0 なので、初期推測値を変更する必要があります。
ライブラリへの定義の読み込み
Libraryフォルダには、各カテゴリの回帰曲線の定義をもつテキストファイルがあります。このテキストファイルをライブラリにロードして、一般回帰曲線の当てはめに使用することができます。
- テキストファイルをライブラリにロードするには:
- マクロ>ライブラリ、または回帰曲線>一般>ライブラリを選択します。
- ファイル>開くを選択します。
- Libraryフォルダから回帰曲線のカテゴリを開きます。
- ライブラリを一読し、使用する回帰曲線の簡易リファレンスや未知の値の個数を確認します。
- ファイル>閉じるを選択します。
これで一般回帰曲線の当てはめにこのライブラリ定義を使用できるようになりました。回帰曲線の定義ダイアログに定義を入力するときに、ライブラリ定義を使用して初期推測値を入力することができます (例:gaussfit(1,5,1,10)) 。KaleidaGraph は、回帰曲線を当てはめる前に必要な置き換え処理を実行します。
一般回帰曲線の適用
- 一般回帰曲線の適用方法:
- 回帰曲線を適用するプロットを開いてください。
- 回帰曲線メニューの一般サブメニューから、回帰曲線を選択してください。 回帰曲線の選択ダイアログが表れます。従属変数は、列の名前の下に全てリストされます。
- 方程式が入力されていない場合、定義をクリックして入力するか、レファレンスをデータに適用してみてください。終了したら OK をクリックしてダイアログを終えてください。この式をよく使うようであれば、マスターリストに回帰方程式を追加してください。
- 回帰曲線を当てはめる変数のチェックボックスをクリックしてください。Ctrl+A(Windows)、Command+A(Macintosh) で全ての変数が選択できます。
- OK をクリックしてください。進行状況を示すダイアログが表示されます。
| 注意: Ctrl+.(ピリオド)(Windows)、Command+.(ピリオド)(Macintosh)は、一般回帰曲線の適用をキャンセルします。計算およびその結果は破棄されます。 |
データの重み付け
一般回帰曲線には、データを重み付けするオプションがあります。一般回帰曲線の定義ダイアログで加重データをチェックすると、曲線を当てはめる際、データに重みが付けられます。これらの重みはデータウィンドウの指定列から取られます。重みは分析データの個々のエラー値を表したものです。
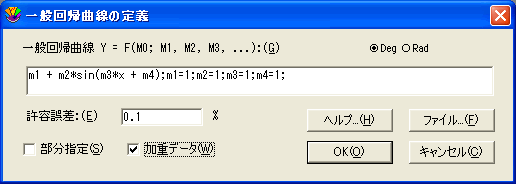
各重みは内部的に 1/((weight)^2) として使用されます。データポイントに 1.0 より小さい重みを指定すると、そのポイントの内部的重みが増加させられ、エラー合計が大きくなります。1.0 より大きい重みは内部的重みを減少させます。加重データをチェックしないと、重みとして 1.0 が使用されます。
偏微分係数の指定
KaleidaGraph が一般回帰曲線を得るための再帰計算に使用するアルゴリズムには、各パラメータに関して関数の偏微分係数を計算する必要があります。回帰曲線の定義ダイアログには、偏導関数を定義可能な部分指定というオプションが備えられています。
偏微分係数を指定する最大の利点は、高い正確さが得られることです。回帰曲線アルゴリズムはこの偏微分係数を使用して、各再帰計算後に最適解を見つけられる数値に移動します。一般的に表面上の微分係数は正確に近似されないことがあるので、実際の偏微分係数が適しています。
偏微分係数の一部だけを指定することができます。正しくない係数を指定するよりも、KaleidaGraph に係数の近似計算を行わせるほうがより正しい結果が得られます。偏微分係数を指定しない場合、KaleidaGraph がその係数を近似計算します。Curve Fits フォルダ (Examples フォルダ) の大部分の回帰方程式に偏導関数が追加されました。
- 偏微分係数を指定するには:
- 一般回帰曲線の定義ダイアログの部分指定チェックボックスをオンにします。ダイアログに、テキストフィールドと各編微分係数を指定するためのボタンが 9 つ表示されます。
- 対応するボタンをクリックし、テキストフィールドに係数を入力して、偏微分係数を入力します。
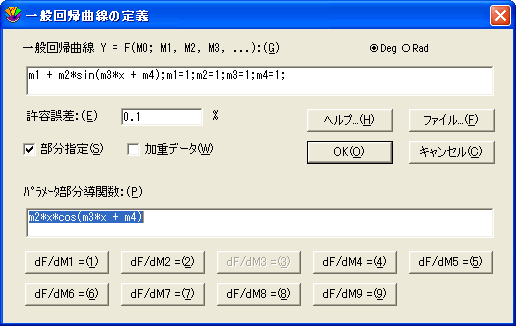
注意: 一般回帰曲線の定義ダイアログのファイルボタンをクリックしてテキストエディタを表示し、テキストエディタに偏微分係数をすべて入力することもできます。テキストエディタには、回帰曲線の定義と指定する偏微分係数が表示されます。例を示します。
m1+m2*m0^m3;m1=0;m2=1;m3=1
1
m0^m3
m2*m0^m3*ln(m0) |
| この例の最初の行は回帰曲線の定義、2行目は m1 の偏微分係数、3行目は m2 の偏微分係数を示し、以降の行は同様に偏微分係数を示します。この回帰曲線のパラメータは3つなので、偏微分係数は 3 つだけ必要です。 |
|
独立多変数の曲線の当てはめ
table 関数を使って、KaleidaGraph は独立多変数の回帰方程式を適用することができます。
たとえば y=a*x+b*x2+c では、a*x+b*table(m0,x col,x2 col)+c という回帰曲線が適用されます。データウィンドウの該当する列が、x col と x2 col に置き換えられます (たとえば table(m0, c0, c2) の場合)。table 関数を使うと、x の各値に対して x2 列の値を使って回帰曲線の計算を実行することができます。
回帰曲線パラメーターの極限設定
回帰曲線パラメーターの極限は 2通りの方法で設定することができます。第一の方法は、パラメーターに条件付きのテストを用いることです。第二の方法は、デフォルトライブラリから limit 関数を用いる方法です。
データに当てはめる直線を一般回帰曲線で定義すると仮定します。方程式は a+b*x のような形式をとります。この例では、b の値を制限したいので、b は負の値ではありません。
一般回帰曲線の定義ダイアログで、次のどちらかの定義を入力します。
| a+(b=(b<0)?0:b)*x; a=1; b=1 or a+(b=limit(0,1000,b))*x; a=1; b=1 |
最初の定義は、b が 0 以下かどうかを調べる条件付きのテストが行われます。もし、それが真である場合は、b は 0 に設定され、偽の場合、b はその値が設定されます。
2番目の定義は、極限関数が用いられます。極限関数は、パラメーターの上下の極限を設定する必要があります。この場合、0 と 1000 は b の極限を制限するために使われています。
一般回帰曲線の定義でパラメータを制限するときには、偏微分係数の指定を行わなければなりません。この指定を行わない場合、単係数の行列エラーが起こる確率が非常に高くなります。この問題は、制限されたパラメーターが、複数反復の境界点に設定されている時に起こりやすくなります。
一般回帰曲線とマクロ計算機
一般回帰曲線の計算は、マクロ計算機で行われます。一般回帰曲線を適用した後、マクロ計算機のメモリレジスタを見ると関連するデータが残されています。メモリレジスタとそのデータは次のような関係にあります。
| m0 |
R 値 |
| m1~m9 |
パラメータの値 |
| m22 |
カイ2乗 |
| m23 |
% エラー項 |
| m24 |
最後の反復のカイ2乗 |
| m25 |
実行された反復の数 |
| m26 |
回帰のパラメータの数 |
|
| 注意: ほとんど全てのメモリレジスタ、アルファレジスタ、プログラム可能なメモリ領域は、一般回帰曲線の実行中、書き変えられています。 |
回帰曲線の結果を使いこなす
回帰方程式の表示
回帰方程式は、プロットメニューの数式表示をチェックすると、表示することができます。一般、線形、多項式、指数、対数、そして累乗のどの回帰曲線の結果も、プロットウィンドウに表示することができます。ただ結果を表示するだけではなく、回帰分析が変更されれば、その結果も自動的に反映されます。
回帰曲線のタイプによって、数式はテーブルで、あるいはテキストラベルで表示されます。一般と多項式は、式が他より長いのでテーブル形式で表示されます。選択ツールを使ってダブルクリックすれば、数式の表示は編集することができます。
式の形式は、プロットメニューの数式ラベルの形式で変更できます。オプションには、桁数、ゼロの表示などがあります。
回帰方程式の係数の表示
- 回帰方程式の係数を表示する方法:
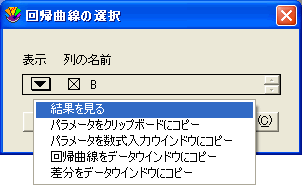
- 回帰曲線メニューから回帰曲線を選択してください。回帰曲線が適用された変数を示す表示の下に、ドロップダウンメニューをもった回帰曲線の選択ダイアログが表れます。
- ドロップダウンメニューの一つをクリックし、表れたポップアップメニューから結果を見るを選択します。回帰曲線の係数を示すダイアログが表れます。
 |
| ↓ |
 |
- クリップボードにコピーを選択すると、係数がクリップボードにコピーされ、他のウィンドウあるいはプログラムで利用することができます。
- 計算機にコピーを選択すると、マクロ計算機に係数がコピーされ利用することができます。
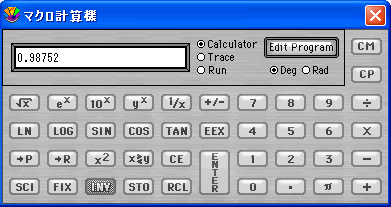
- OK をクリックしてプロットウィンドウに戻ってください。
相関係数
回帰方程式、係数とともに相関 (R または R^2) も表示されます。相関は、計算された曲線がどれだけよく元のデータに当てはまっているかを示します。この値は 0 から 1 の間をとり、1 に近いほうがよりよいことを示します。
R および R^2 値は、通常、0 から 1 の間の値をとります。回帰曲線では、R^2 の値が負をとる場合もあります。これは、生成された曲線のデータへの適合が、すべての Y 値の平均値を通過する水平直線より悪い場合に発生します。間違った回帰方程式を選択しているか、外れ値が非常に多いデータを適合しようとしていることが原因です。
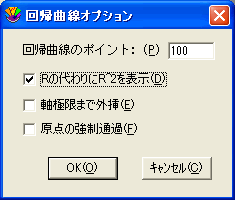
結果の一部として線形相関関数 (R) と決定係数 (R^2) のどちらを表示するか選択できます。回帰曲線オプションダイアログ (回帰曲線メニュー) の R の代わりに R^2 を表示チェックボックスで選択します。
次に、R の計算に使用する方程式を紹介します:
- ポアソンの R (最小2乗法)
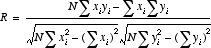
- ポアソンのR (一般の回帰曲線)
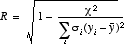
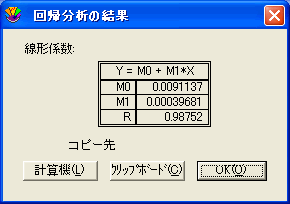
パラメータエラー
一般回帰曲線はパラメータの値の右に、エラー値を表示します。エラーは、パラメータの標準誤差です。これらの値は、パラメータの値±エラー値 と読むことができます。
カイ2乗値
一般回帰曲線では、カイ2乗値が表示されます。この値は、元のデータと計算された曲線間のエラー値の 2乗の総計を表しています。一般的にはカイ2乗値が低いほど、よく曲線が当てはまっています。
カイ2乗の計算式は以下の通りです。
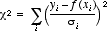
クリップボード、計算機へのパラメータのコピー
- クリップボードまたはマクロ計算機にパラメータをコピーする方法:
- 回帰曲線メニューから回帰曲線を選択してください。回帰曲線が適用された変数を示す表示の下に、ドロップダウンメニューをもった回帰曲線の選択ダイアログが表示されます。
- クリップボードにコピーするには、ドロップダウンメニューのパラメータをクリップボードにコピーを選択してください。こうすることによって、他のウィンドウあるいはプログラムで結果を利用することができます。
- 注意: プロットウィンドウに結果をコピーしても、係数は回帰曲線がアップデートされるまで変わりません。このため、 数式表示コマンドを使ったほうがよいでしょう。
- マクロ計算機にコピーするには、ドロップダウンメニューのパラメータを計算機にコピーを選択してください。こうすることによって、マクロ計算機で結果を利用することができます。
- OK をクリックしてプロットウィンドウに戻ってください。
| 注意: ポップアップメニューの結果を見るを選んで、クリップボードまたは計算機ボタンを押してもコピーできます。 |
回帰曲線の値をデータウィンドウにコピー
- 回帰曲線の値をデータウィンドウにコピーする方法:
- 回帰曲線メニューから回帰曲線を選択してください。回帰曲線が適用された変数を示す表示の下に、ドロップダウンメニューをもった回帰曲線の設定ダイアログが表れます。
- ドロップダウンメニューから回帰曲線をデータウィンドウにコピーを選択してください。
- OK をクリックし、プロットウィンドウに戻ってください。
カレイダグラフは、データウィンドウに結果を付け加えます。第1列は x 変数の値です。元の x 値を使用する加重曲線を除いて、x 変数の数は、形式メニューの回帰曲線オプションダイアログで設定された回帰曲線のポイント数に等しくなります。第2列は、各ポイントにおける回帰曲線の値が入力されます。
| 注意: もし独自の x 値を与えたい場合は、回帰曲線の値を計算するために数式入力を使ってください。 |
残差をデータウィンドウにコピー
- 残差をデータウィンドウにコピーする方法:
- 回帰曲線メニューから回帰曲線を選択してください。回帰曲線が適用された変数を示す表示の下に、ドロップダウンメニューをもった回帰曲線の設定ダイアログが表れます。
- ドロップダウンメニューから残差をデータウィンドウにコピーを選択してください。
- OK をクリックし、プロットウィンドウに戻ってください。
カレイダグラフは、データウィンドウに残差を付け加えます。これらの値は、元の Y 値と回帰曲線によって計算された値の差を表します。
数式入力を使用して回帰曲線から値を得る
数式入力の回帰曲線メニューには、回帰曲線の値の分析に使用可能なコマンドが備えられています。これらのコマンドを使用して、曲線の任意のポイントの値を求めたり、回帰曲線とオリジナルデータの間の残差を求めることができます。
回帰曲線が軸極限まで外挿の場合を除き、X 値がデータのオリジナルの範囲内にある場合に限り結果が正確になります。値がこのデータ範囲から大きく外れている場合、結果は線形的に補間されます。
| 注意: 回帰曲線から値を取得するには、プロットを作成し、回帰曲線をデータに適用する必要があります。これを行なわずに数式を実行しようとすると、エラーメッセージが表示されます。 |
- 回帰曲線から値を計算するには:
- 目的の変数を含むデータウィンドウをアクティブ化します。
- ウィンドウ>数式入力 を選択します。
- 数式をウィンドウに入力します。数式は z=fit(x,y) の形式で入力します。
- z は宛先列です。
- x は単一の値か X値を含む列です。
- y は適用する回帰曲線を含む列です。
- fit は、数式入力の回帰曲線メニューから適切なコマンドに置き換えられます。
- 実行をクリックして数式を実行します。宛先列に特定の X 値における回帰曲線の値が入力されます。
回帰曲線の削除
回帰曲線の削除
回帰曲線は、プロットに追加するのと同じ方法で削除することができます。回帰曲線を適用すると、回帰曲線メニューの曲線の名前にチェックマークが付けられます。
- 回帰曲線を削除する方法:
- 回帰曲線メニューから、削除したい曲線の名前を選択します。変数のリストを含むダイアログが表示されます。当てはめられた各変数はチェックされています。
- 削除したい回帰曲線のチェックボックスのチェックを外します。選択解除ボタンをクリックすると、一度に全てのボックスのチェックが外されます。
- OK をクリックすると、プロットに戻り、回帰曲線が削除されます。関連する方程式も削除されます。
回帰曲線のその他の機能
回帰曲線の表示の変更
- 回帰曲線のラインスタイル、ライン幅、カラーを変更するには:
- プロットウィンドウをアクティブにした状態で、プロット>変数設定を選択します。
- 編集する変数を選択します。
- 回帰曲線設定タブをクリックして、回帰曲線を変更します。
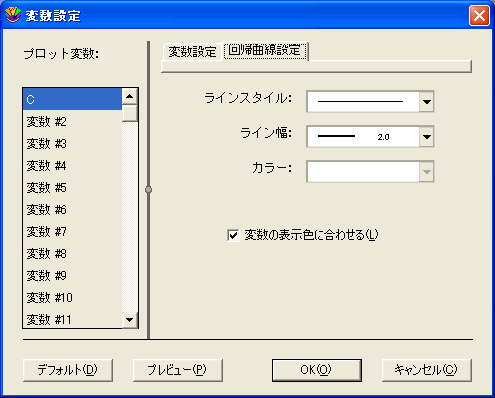
- ラインスタイルを変更するには、ラインスタイルポップアップメニューから選択します。
- ラインの幅を変更するには、ライン幅ポップアップメニューから選択します。
- ラインの色を変更するには、カラーポップアップメニューから選択します。
- OK をクリックして、プロットに戻ります。
| 注意: 回帰曲線に変数と同じ色を使用する場合は、回帰曲線設定タブで変数の表示色に合わせるを選択します。 |
回帰曲線を表す数式の表示の変更
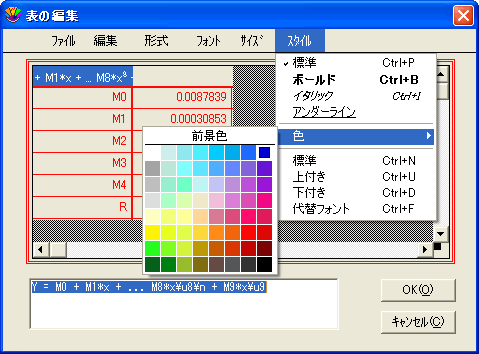
- 表示色の変更
最初に回帰曲線を当てはめた時点では、回帰曲線とその数式の表示色は同一になっています。多項式曲線と一般回帰曲線では、結果の表をダブルクリックして回帰曲線の結果の表示色を変更することができます。その他の回帰曲線の場合は、プロット>テキストオプションを選択し、テキストと変数カラーのリンクチェックボックスからチェックを外す必要があります。チェックが外れたら、方程式をダブルクリックして方程式の色を変更できるようになります。
 |
| ↓ |
 |
- パラメータの精度や表記の変更
回帰曲線の数式で使用される値の精度は、数式ラベルの形式コマンドで規定されます。このコマンドを使用して、表示される結果の有効桁数を増やすことができます。また、数学的、または工学的な表記で結果を表示することもできます。
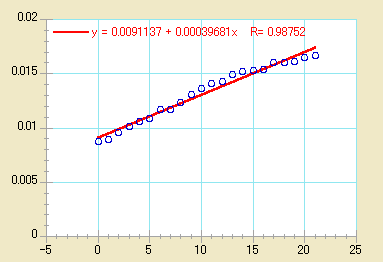
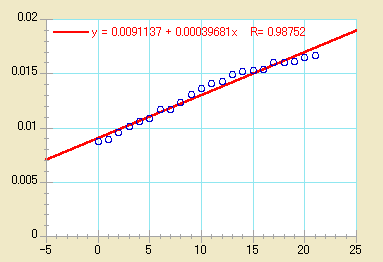
極限値の外挿
カレイダグラフは通常、独立した各軸の最小および最大値の間に回帰曲線を表示します。しかし、軸極限に回帰曲線を外挿することもできます。回帰曲線の外挿された部分は、計算式に基づいています。
| 注意: スムース曲線 (スムース、加重、3次元スプライン、および補間) については、単一の方程式で表すことができないので、外挿することができません。 |
- 極限値を外挿する方法:
- 形式メニューから回帰曲線オプションを選択します。
- 軸極限まで外挿チェックボックスをクリックします。
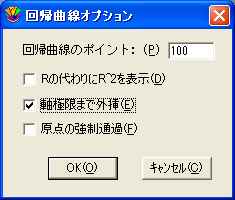
- OK をクリックして、ダイアログを終了します。回帰曲線を再計算した後、プロットが再描画され、回帰曲線が軸極限に拡張されます。
 |
| ↓ |
 |
原点を通る線形回帰曲線
デフォルト(標準設定)では、線形回帰曲線が適用されたとき、傾きと切片が計算されます。KaleidaGraph は傾きだけを求めるために、原点 (0, 0) を通る回帰曲線を適用するオプションがあります。
- 原点を通る線形回帰曲線の適用方法:
- 形式メニューの回帰曲線オプションを選択してください。
- 原点の強制通過チェックボックスをクリックします。
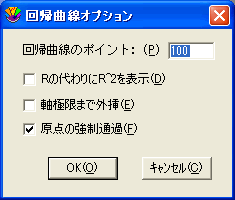
- OK をクリックし、プロットに戻ってください。線形回帰曲線は、Y軸の交点が 0 で再計算されます。ただし、R または R^2 値は結果の方程式では抑えられます。
 |
| ↓ |
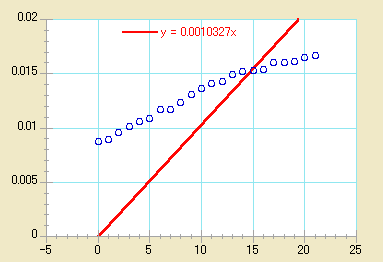 |
回帰曲線のポイント数を増加
回帰曲線を適用するときには (加重を除く)、KaleidaGraph は既定のポイント数分を回帰曲線に沿って計算します。これらのポイントは、回帰曲線を描いたり、回帰曲線から値を計算するために使用されます。数式入力を使ってデータウィンドウに回帰曲線の値を渡す際、ポイント数を増加すると有効です。これによって、値がより正確になります。
- 回帰曲線のポイント数を増加させる方法:
- 形式メニューから回帰曲線オプションを選択します。
- 回帰曲線のポイントに異なる値を入力してください。すでにプロットされているポイント数から増やしていくとよいでしょう。またデータに多数の山や谷がある場合、ポイントをもっと増やしてみるとよいでしょう。
- OK をクリックして、プロットウィンドウに戻ってください。
回帰曲線のみの表示
元のデータポイントなしで、回帰曲線だけを表示したい場合もあります。これは、プロットが散布図でない場合に限り、変数設定ダイアログで設定できます。
- 回帰曲線のみの表示方法:
- プロットウィンドウをアクティブにした状態で、プロット>変数設定を選択します。変数設定ダイアログが表示されます。
- 編集する変数を選択します。
- マーカーの表示とラインスタイルポップアップメニューでなしを選択します。 すると元図からマーカーとラインが消されます。
- OK をクリックします。
エラーバーを使いこなす
概要:エラーバーを使いこなす
エラーバーはプロットデータの誤差の範囲を示しています。エラーバーは通常、データポイントからの延長線で表示され、両端のキャップは広がりの高値と低値を表しています。エラーバーの扱い方を以下に説明します。
エラーバーの追加 (関連:クイックスタートガイド「エラーバーの追加」)
- エラーバーの追加方法:
- エラーバーを追加するプロットを選択します。
- プロットメニューからエラーバーを選択し、エラーバー変数ダイアログを表示させます。各プロット変数が一覧表示され、2つのチェックボックスがその前に置かれます。
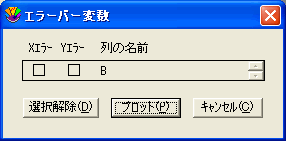
- エラーバーを追加する変数のチェックボックスの一つをクリックします。 エラーバー設定ダイアログが表示され、特定セットのエラーバーについてオプションを指定することができます。
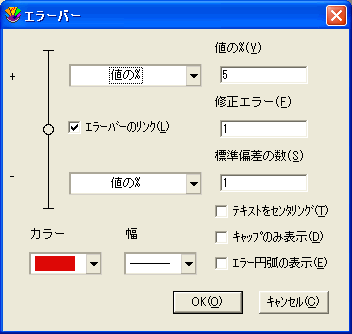
- エラーバーの色や線の太さなどを設定し、OK をクリックしてください。
- 希望する変数全てについてエラーバーの設定が終わるまで、ステップ 3 と 4 を繰り返します。
- プロットボタンをクリックすると、プロットの変数にエラーバーを追加します。プロットが再描画され、エラーバーが表示されます。
データ列からのエラー値のプロット
気に入ったエラータイプがない場合は、エラー値を自分で決め、それをエラーバーにプロットすることができます。
- データ列からエラー値をプロットする方法:
- データウィンドウで、エラー値のデータ列を作ります。
- エラーバーを加えるプロットを選択します。
- プロットメニューのエラーバーを選択して、エラーバー変数ダイアログを開いてください。
- エラーバー設定ダイアログを表示するため、チェックボックスの一つをクリックしてください。
- エラータイプのポップアップメニューでデータ列を選択して、エラー値を含む列を指定してください。
- OK をクリックし、さらにプロットをクリックしてください。
片面のエラーバーの作成
片面のエラーバーは、データポイントの片面にだけバーを表示する場合に役立ちます。単一のエラータイプを選択することができ、バーの正または負のどちらを表示するかを決定することができます。
このようなエラーバーの特別なケースは、データ列からエラー値をとった場合に生じます。エラーバーの方向はデータの符号によって判定され、正あるいは負のエラータイプが選択されます。正のデータについては、エラータイプと同じ方向にバーが表示されます。負のデータについては、バーは反対方向に表示されます。
- 片面のエラーバーの作成方法:
- エラーバーを追加するプロットを選択します。
- プロットメニューからエラーバーを選択すると、エラーバー変数ダイアログが表示されます。
- チェックボックスの 1つをクリックすると、エラーバー設定ダイアログが表示されます。
- エラーバーのリンクチェックボックスのチェックを外します。
- 正あるいは負のエラータイプポップアップメニューのどちらかを、なしに設定します。
- 表示される他の部分について設定してください。
- OK をクリックして、このダイアログを終了します。
テキストエラーバーの追加
テキストラベルはエラーバーとしても使用できます。これはテキストラベル付きのプロット上で特定のマーカーや列に注釈を付けるために使用します。テキストデータ列をエラータイプに指定すると、列のデータはプロット上の対応するポイントにテキストラベルとして表示されます。エラーのデータ列が対応しているデータポイントだけ、テキストラベルが表示されます。
ラベルの方向は選択されたエラータイプと同じ方向になります (Xエラーは水平に、Yエラーは垂直に)。テキストをセンタリングにチェックすると、ラベルはマーカーの中央に置かれます。チェックしなければ、エラーが選択されたマーカーの横に位置を揃えて置かれます。テキストラベルはテキストツールで個別に、選択ツールでグループとして移動できます。
| 注意: デフォルトでは、フォントとスタイルは値ラベルと同じになります。これらのラベルはその中で使用される下付き文字、上付き文字あるいは代替フォントを持つことができます。 |
- テキストエラーバーの追加方法:
- データウィンドウで、ラベルとして表示したいデータをテキスト列に置きます。
- エラーバーを追加するプロットを選択します。
- プロットメニューからエラーバーを選択すると、エラーバー変数ダイアログ.が表示されます。
- チェックボックスの 1つをクリックすると、エラーバー設定ダイアログが表示されます。
- エラーバーのリンクオプションのチェックを解除します。
- バーの一方のポップアップメニューをなしに設定します。もう一方についてはデータ列を選択し、ラベルを含むテキスト列を指定します。
- マーカーの中央にラベルを置く場合には、テキストをセンタリングにチェックします。もしチェックがなければ、ラベル同士が揃えられて配置されます。
- OK をクリックして、ダイアログを終了します。
| 注意: エラーバーのリンクがチェックされ、テキストのセンタリングがチェックされていない場合は、テキストラベルはマーカーの両側に置かれます。 |
関連:プロット作成例:「テキストエラーバーを使用してプロットに注釈を追加する」
エラー円弧の追加
エラーバーの代わりにエラー円弧を表示することも可能です。そのためには、エラーバーダイアログでエラー円弧の表示オプションをチェックします。エラータイプポップアップメニューのどちらかがなしの場合、円弧が表示されます。X エラーと Y エラーについて、それぞれ正と負のエラーが選択されている場合には、楕円が表示されます。
楕円の四分円は別々に制御されます。これは、垂直距離が Y エラーによって決定され、水平距離が X エラーによって決定されるからです。これによって、様々なエラー円弧や楕円を表示することができます。
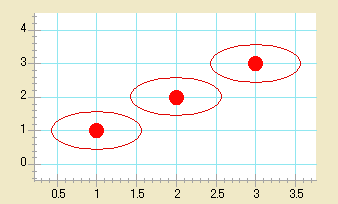
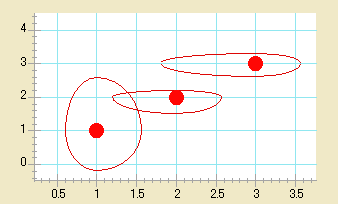
- エラー円弧を追加するには:
- エラー円弧を追加するプロットを選択します。
- プロットメニューからエラーバーを選択すると、エラーバー変数ダイアログが表示されます。
- Xエラーをチェックし、エラーバー設定ダイアログを開きます。
- エラー円弧の表示をチェックします。
- 正負のエラータイプポップアップメニューの設定をして、OK をクリックしてください。
- Yエラーをチェックし、円弧の垂直方向の設定を行います。ステップ 4 と 5 を繰り返してください。
- プロットをクリックし、プロットウィンドウに戻ってください。
キャップのみの表示
データポイントとエラーキャップを結び付けるラインを削除することができます。これは、エラーバーダイアログのキャップのみ表示オプションを選択すると、実行されます。
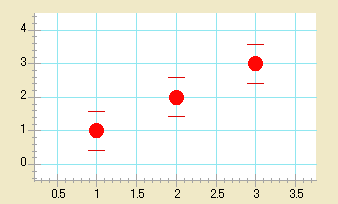
このオプションはプロットから不必要なラインを削除し、データを見やすくします。この機能は、標準偏差エラータイプが選択されているときに最も有効です。エラーバーは中間値から描かれるので、そのポイントとキャップを結ぶラインは必要ありません。ラインを削除し、キャップの長さを調整することによって、プロット全体のエラーラインを点線かベタにすることができます。
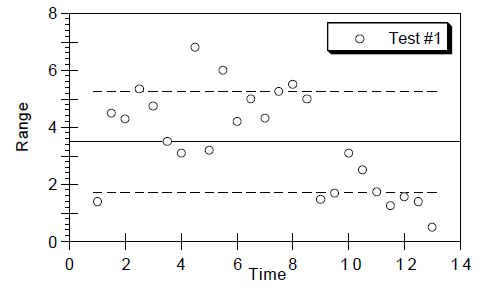
- エラーキャップのみを表示させるには:
- エラーバーを追加するプロットを選択します。
- プロットメニューからエラーバーを選択し、エラーバー変数ダイアログを開いてください。
- チェックボックスをクリックし、エラーバー設定ダイアログを表示してください。
- キャップのみ表示オプションを選択します。
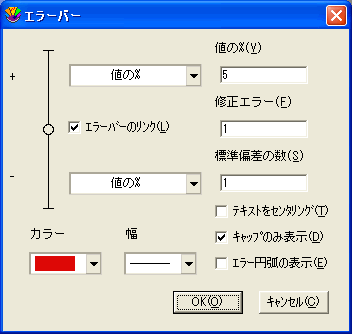
- 正負のエラータイプポップアップメニューの設定をしてください。
- OK をクリックしてください。
キャップの長さの変更
- キャップの長さの変更方法:
- プロット>プロットオプションメニューから一般を選択してください。
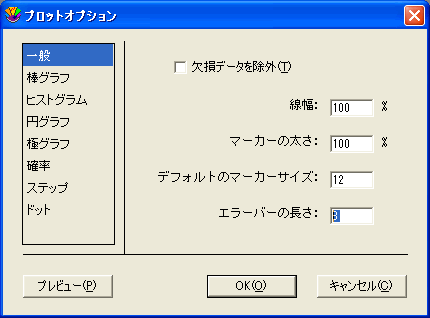
- エラーバーの長さの値を変更してください。ゼロが入力されると、キャップは見えなくなります。
- OK をクリックして、プロットに戻ってください。
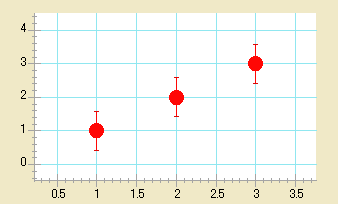
エラーバーの削除
エラーバーは、プロットの個々の変数から、あるいは全ての変数から一度に、簡単に削除することができます。
- エラーバーの削除方法:
- プロットメニューのエラーバーを選択して、エラーバー変数ダイアログを表示してください。
- 削除するエラーバーのチェックボックスのチェックを外してください。選択解除をクリックすると、一度に全てのチェックボックスのチェックが外せます。

- プロットをクリックして、プロットウィンドウに戻ってください。
|

