ヒューリンクステクニカルサポート

TableCurve 2D/3D サポート情報

TableCurve 2D / 3D 製品ページ

更新日： 14/04/15

2. パラメトリック関数のフィッティング

ここでは、パラメトリックモデルを用いたフィッティングを説明します。パラメトリックモデルは、データの特性を表すパラメータの解が得られます。補間や外挿を行う近似関数とは異なり、パラメータの推定とパラメータ間の相互作用がポイントとなります。

パラメトリック関数
薬理学的データセットのインポート
X=0、Y=0データ
TableCurve のエディタ
推移関数 (Transition Functions)
推移関数によるフィッティング
推移関数によるフィッティングのカスタマイズ
推移方程式のレビュー
極値累積分布
数式のスキャン
フィットの参照カーブ
信頼区間と予測区間
残差
Stabilized Normal Probability Residuals Plot
計算値の要約
データの要約
第1次導関数と累積分布の表示
ポイント毎の残差
ユーザー定義関数 (UDF)
UDF Auto Adjust

1. パラメトリック関数

パラメトリックモデルを適用する際、実際のデータを見ればわかりますが、その現象の理論的な背景を知っている必要はありません。「理論的な背景」とは、エネルギや濃度、時間、温度などの物理量を変数とする現象のメカニズムを意味します。

理論的な背景のあるモデルでは、独立変数 x と従属変数 y との間で何らかの物理的原理が働いています。

パラメトリックモデルは、そのような理論的な背景=物理的原理を説明するためではなく、得られたデータの特徴を説明するために用いられます。ここで用いるサンプルデータも、そのようなデータです。変数同士には、物理的、化学的、生化学的、生理学的、人為的に何らかの関連性があることはわかっていますが、その原理を定量的に説明するためにモデルを適用するわけではありません。

この種の解析では、現象を生み出すシステム（原理）はブラックボックスとして扱い、その傾向や特性をよく表しているパラメータを提示します。人間の生化学的データは、論理的にすべて説明しきれない複雑さをもっています。以下では、この種のデータのパラメトリックなカーブフィッティングの例を示します。

2. 薬理学的データセットのインポート

TableCurve 2D を起動します。
File｜Import メニューコマンド（またはメインツールバーの Import ボタン）をクリックします。Data フォルダの中にある SAMPLE.xls ファイルを開いて下さい。[.xls] ファイルが表示されない場合は、ファイルの種類で Excel [xls] を選択して下さい。

データ列の判別をしやすくするために、TableCurve 2D はワークシートの最初の 100行分の文字列データをリスト表示します。少なくともその中の 1つを選択しなければなりません。
X-variableとして、3列目の (2)Sample2!A: Tour 2: Parametric Functions とラベルの付いた列を選択して下さい。Y-variable には、4列目の (2)Sample2!B: Concentration のラベルの列を選択します。ウィンドウ右側に、データのプレビューが表示されます。

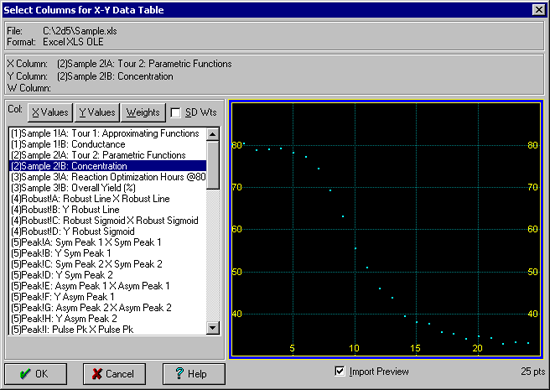
注意：最初に選択した2列は、自動的にXYデータとして読み込まれます。リストの列名をダブルクリックするだけで、選択することができます。XY 変数の列は、重み Weights の列を選択するのと同じように、変更することができます。Weights の列は、複数の Y 列データの標準偏差として使用することもできます。
OK ボタンを押すと、データ列名を編集するダイアログ現れますので、もう一度 OK ボタンを押して下さい。

選択した列データが読み込まれ、その概要が表示されます。データポイント数は 25点です。

データをインポートすると、 Process｜Background Thread Processing で設定された方法で、自動的にフィッティングが実行されます。ここでは、自動フィッティングは無視します。

3. X=0、Y=0データ

最初のデータペアは、X 値が 0.0です。TableCurve 2D は、対数および逆関数を使用できるようにするため 0.0 には 1E-25 を割り当てているので、x=0 のデータポイント（および lny または 1/y 式でフィッティングする場合 y=0）は除外して下さい。他のデータポイントを使ってデータ曲線を作ることができるので、x=0 のデータポイントがなくても問題ありません。そこで、フィッティングを実行する前に、この最初のデータポイントを除外しておきます。

4. TableCurve のエディタ

TableCurve 2D には、2種類のエディタが用意され、グラフィカルにデータの編集が行えます。Edit｜TableCurve Editor メニューコマンドはシンプルなスプレッドシート形式のインターフェイス、Edit｜ASCII Editor はノートパッド形式のインターフェイスとなっています。

Data｜Section Data メニューコマンドまたはボタンで、データを確かめることができます。ここでは、TableCurve Editor を使って、最初のポイントを削除します。

Edit｜TableCurve Editor メニューコマンドまたは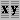ボタンをクリックします。Ex (Exclude) チェックボックスの XY#1 にチェックマークを入れ、OK ボタンを押して下さい。変更したデータを保存するか否かのダイアログが表示されたら、いいえを選択して下さい。

TableCurve 2D のステータスウィンドウには、25 ポイントではなく、24 ポイントのデータが示されます。最初のポイントが非アクティブになっています。

time=0 のポイントでは、濃度が約 80 単位でした。この値は、注射をした直後の血流のレベルに対応しています。数時間後、このレベルは次第に下がり始め、平常レベルの 35 単位付近まで、S字型のカーブを描いて変化してゆきます。

5. 推移関数 (Transition Functions)

このような推移は、薬理学では当たり前ですが、他の科学領域でもよく見られます。ただし、負の傾きではなく正の傾きの方が一般的でしょう。この種の傾向を示す関数は、推移関数、S字関数、累積関数と呼ばれます。

本例では、生化学的な原理をフィッティングによって説明するのが目的ではありません。この現象を特徴づけるモデルは、以下のパラメータが必要だということがポイントです。

上限または下限の濃度
カーブの高さ
カーブ中央の時間
変化のスピードを表すカーブの幅、傾斜または勾配
場合によって、カーブの非対称性を示すパラメータ

パラメトリックモデルは、データの特性を視覚化するのに有意義な方法だという点に注目して下さい。こうしたモデルを繰り返し適用して、生化学的な要因がこれらのパラメータにどのように影響するか調べてゆくのです。

6. 推移関数によるフィッティング

標準で用意されている関数の全リストは、Help｜List Equations メニューコマンドで見ることができます。推移関数は、リストの最後の方の Non-Linear のグループの中にあります。数学的な説明は、Help｜Non-Linear Equations メニューコマンドをクリックし、Transition Functions のリンクをクリックするか、PDF Documents フォルダに入っている NonLinEqns.PDF ファイルを参照して下さい。

TableCurve 2D は、29 の非線形推移関数と、ゼロ切片または切片付きの 14 の推移モデルとインパルスモデルを用意しています。この 15 のモデルのうち、5つが対称形カーブ、10が非対称形カーブです。

本例では、これらの非線形推移関数だけでフィッティングを行います。最適な線形モデルを用いれば、非常によいフィッティング結果が得られます。しかしながら、それは近似関数によるもので、その係数はデータの特性を表すパラメータについて何も提示してくれません。

推移関数は、S字の下限を a、上限を b、カーブの中央を c、カーブの傾きを d で表します。

7. 推移関数によるフィッティングのカスタマイズ

TableCurve 2D は、Peak、Transition、Kinetic 関数のフィッティングに関してそれぞれカスタマイズすることができます。これらの設定は、1個所ですべて行えます。その設定ウィンドウにある AI エキスパートシステムは、データの特徴を調べ、最適な関数とそのオプションを自動設定してくれます。

Process｜Curve-Fit Transition Functions メニューコマンドまたはボタンをクリックし、AI Expert ボタンを押して下さい。

データが明らかに非対称の特性を持っているので、AI エキスパートシステムは対称形関数でむだな時間を浪費しないようにオプションを選択してくれます。また、S字カーブの上限下限もゼロ付近を通らないので、切片付きの関数タイプを選択しています。

非線形のフィッティングは、繰り返し実行されます。そのため、最大繰り返し回数と収束条件の設定が必要です。繰り返しのデフォルト設定値 100 は、複雑な UDF を除いてほぼすべての関数で妥当な回数です。

収束条件のデフォルト設定値 6 は、5回フィッティングを繰り返し、r² の有効数字 6桁目に変化が見られない条件を意味します。

このデータセットには外れ値が存在しないため、誤差が正規分布を外れることはなく、また y 値の範囲もあまり大きくないので、堅牢さを最小にする必要はありません。

本例では、対称形の推移関数を使用します。
Gaussian Cumulative 関数のチェックマークを ON にして下さい。
Fit ボタンをクリックすると、これらの関数でのフィッティングが実行されます。
フィッティングが実行されたら、Graph Start ボタンをクリックして下さい。

8. 推移方程式のレビュー

Review Curve-Fit ウィンドウの List メニューまたは数式リストの Sort メニューで、Sort by F-statistic を選択します。

パラメトリック関数の場合、データの特徴をいかによく表しているか、F 統計量を用いて数式をソートします。

非線形モデルとしてできるだけシンプルな数式を使用します。非線形推移関数には、かなり複雑で長いタイトル（数式）を表示するものもあります。
Review Curve-Fit ウィンドウの File｜Preferences メニューコマンドをクリックし、Notational Format for Non-Linear Equations オプションのチェックボックスが ON になっていることを確認し、OK ボタンを押して下さい。

ソートされた順番を比較するために、数式リストに 4つの統計量を表示させます。
Equation ウィンドウの List メニューまたは Review Curve-Fit ウィンドウの List メニューで、All Goodness of Fit in List オプションをチェックして下さい。

9. 極値累積分布

F 統計量で最上位にランクされたのは、4パラメータの極値累積分布関数です。この関数は、非常によくデータに当て嵌まっています。F 統計量が大きいほど、データとモデルが一致しています。この式の F 統計量は 7287 で、データのノイズによく対応しています。

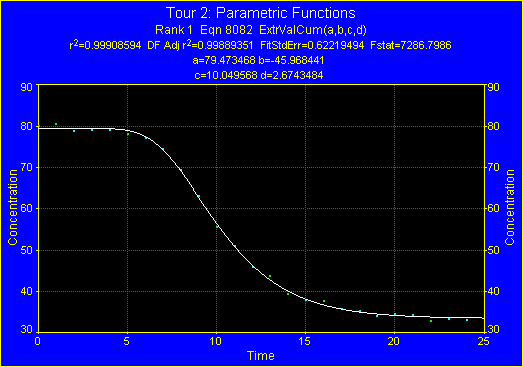
3番目の非対称形シグモイド（逆非対称）は 5パラメータで、r² は最もよく、標準誤差も低いことに注目して下さい。

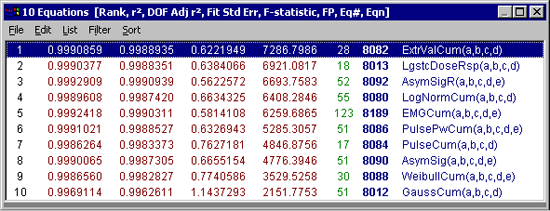
非対称形シグモイドモデルが最小2乗法フィッティングでは最良の結果を出しますが、5パラメータ必要とするのに対して、極値累積分布モデルは 4パラメータですむため、F 統計量は後者の方がよいモデルだと判断しています。

10. 数式のスキャン

Review Curve-Fit ウィンドウのボタンを使って、数式リストのその他の関数も調べることができます。

数式は、数式リストの中で直接クリックしたり、数式リストがカレントウィンドウの場合はキーボードの矢印キーを使って、また Review Curve-Fit ウィンドウの Scan メニューを使って探すことができます。マウスにホイールが付いている場合は、Review Curve-Fit ウィンドウをカレントウィンドウにして、ホイールでスクロールさせることができます。

用量反応ロジスティック関数 LgstcDoseRsp(a,b,c,d) と対数正規累積関数 LogNomCum(a,b,c,d) の 0 における未定義部分、およびパルス累積関数 PulseCum(a,b,c,d) とワイブル累積関数 WeibullCum(a,b,c,d,e) のカーブの急な導入部を除いて、非対称形推移モデルのグラフはどれも区別がつけられません。極値累積分布関数と他の関数とを比べて見ましょう。

11. フィットの参照カーブ

極値累積分布関数 ExtrValCum(a,b,c,d) を選択し Add Current Equation as Reference ボタンまたは Reference｜Add Current Equation as Reference メニューコマンドをクリックして下さい。

最初、元のカーブと参照カーブは同一で、重なり合っています。
ボタンをクリックして他の関数に移動すると、参照カーブとの違いを見ることができます。

微妙な違いもわかります。
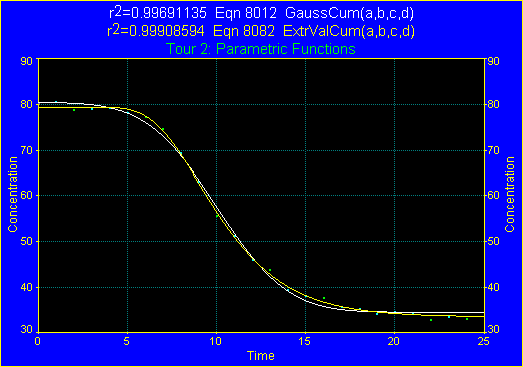
Toggle Display of Equation References ボタンを使って、参照カーブの表示を ON/OFF することができます。
ボタンをクリックすると、最上位の極値累積分布関数に戻ります。

12. 信頼区間と予測区間

信頼区間は、フィッティングを繰り返して得られた平均曲線の誤差範囲を表します。予測区間は、個々のフィッティング曲線が通る範囲を表します。予測区間は、信頼区間よりも幅が広くなります。このデータでは、フィッティングを繰り返した結果の平均が重要ですので、信頼区間のみを使用します。

ツールバーの Set Confidence/Prediction Intervals, %Confidence ボタンをクリックします。Confidence Intervals のチェックボックスを ON、Prediction Intervals を OFF、99% Confidence を ON にして OK ボタンを押して下さい。
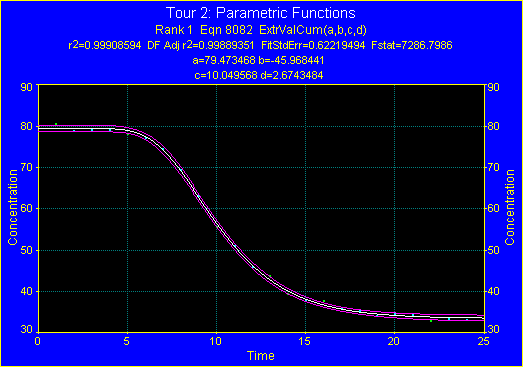
各関数の信頼区間の幅をチェックして下さい。

ワイブル累積関数 WeibullCum(a,b,c,d,e) の場合はカーブ導入部で、幅が広くなっている点に注意して下さい。
すべての信頼区間をチェックしたら、Show Confidence/Prediction Intervals ボタンをクリックして信頼区間を非表示にし、再度、極値累積分布関数に戻って下さい。

13. 残差

Resid ボタンをクリックして、極値累積分布関数の残差を表示させてください。関数毎に残差のランダムさが異なるのがわかります。

Y 軸タイトル末尾に付いている数字は変動回数、すなわち X 範囲内で残差の正負が切り替わった回数です。すべての関数を比べるとあまり大きな違いはありませんが、非対称形シグモイド関数で変動回数が最大で、フィット標準誤差は最小になることに注意して下さい。

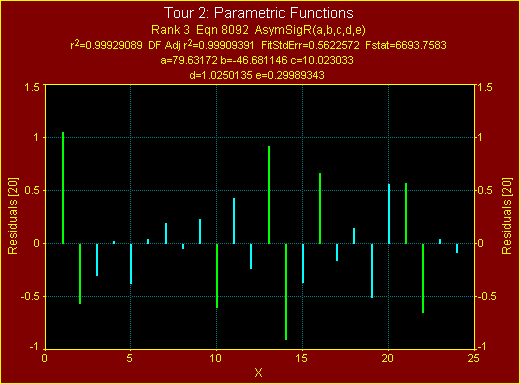
残差を観察して系統的に同じような傾向があるときは、通常、モデルとしては不適切あるいは不完全である場合が多いです。数式リストに追加した Gaussian Cumulative 関数に、その典型的な特徴が現れています。

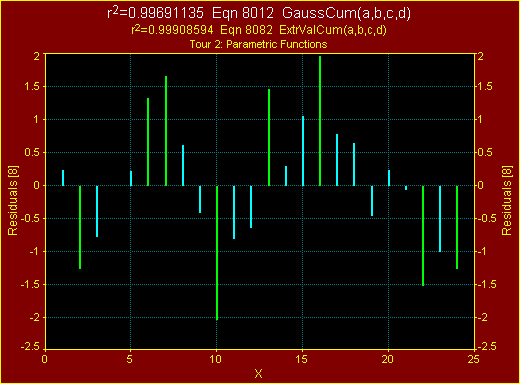
残差は通常、標準誤差や信頼区間が有効になるように分布しなければなりません。

14. Stabilized Normal Probability Residuals Plot

View Residuals ウィンドウのツールバーにある Display Residuals in Stabilized Normal Probability Plot ボタンをクリックして下さい。

注意：残差の表示変更ボタンはウィンドウ左側にも表示されます。

Δ (デルタ) SNP グラフでは、モデルが完全にデータに当て嵌まった場合は y=0 のライン上に残差がプロットされ、その上下に臨界線が引かれます。TableCurve 2D は、90%、95%、99%、99.9% の臨界線を引きます。99% 臨界線とは、100 のデータセットのうちの 1つだけが、臨界線を超えたポイントを少なくとも 1つもつということを意味します。

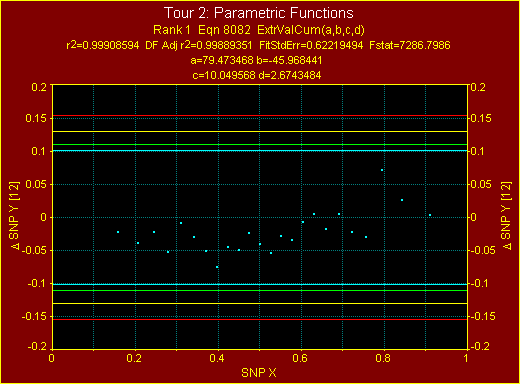
このサンプルでは、すべての関数で 90％臨界線の中にすべてのデータポイントが収まっており、ガウス誤差を容易に確認できます。
Display Basic Residuals ボタンをクリックして、通常の表示に戻って下さい。
View Residuals ウィンドウの閉じるボタンまたは Review Curve-Fit ウィンドウの Resid ボタンを押してウィンドウを閉じて下さい。
関数は、数式リスト最上部の極値累積分布関数にして下さい。

15. 計算値の要約

Numeric ボタンを押して Numeric Summary ウィンドウを表示させ、極値累積分布関数の計算値の要約を見て下さい。

Rank 1  Eqn 8082  ExtrValCum(a,b,c,d)

r² Coef Det    	DF Adj r²      	Fit Std Err    	F-value
0.9990859398   	0.9988935060   	0.6221949450   	7286.7986262

Parm  	Value        	Std Error    	t-value      	99% Confidence Limits     	P>|t|

a    	79.47346826  	0.281909107  	281.9116744  	78.67134111  	80.27559541  	0.00000
b    	-45.9684411  	0.413311267  	-111.219908  	-47.1444520  	-44.7924301  	0.00000
c    	10.04956768  	0.062296479  	161.3183907  	9.872313038  	10.22682232  	0.00000
d    	2.674348365  	0.076175292  	35.10781902  	2.457603788  	2.891092942  	0.00000

Area Xmin-Xmax 	Area Precision
1212.0510118   	1.4381e-17

Function min   	X-Value        	Function max   	X-Value
33.677619403   	24.000000000   	79.473468201   	1.0000017963
1st Deriv min  	X-Value        	1st Deriv max  	X-Value
-6.323351375   	9.0693820931   	-4.679e-07     	1.0000015911
2nd Deriv min  	X-Value        	2nd Deriv max  	X-Value
-1.986044726   	6.4955283716   	1.0355597619   	11.643241597

Procedure      	Minimization   	Iterations
LevMarqdt      	Least Squares  	7

r² Coef Det    	DF Adj r²      	Fit Std Err    	Max Abs Err
0.9990859398   	0.9988935060   	0.6221949450   	1.1885317988

Source   	Sum of Squares    	DF      	Mean Square        	F Statistic      	P>F
Regr     	8462.7396         	3       	2820.9132          	7286.8           	0.00000
Error    	7.742531          	20      	0.38712655
Total    	8470.4822         	23

Date           	Time           	File Source
May 5, 2000    	9:31:39 PM     	c:\2d5\tour2.sav

t-値（t-value）は、各パラメータの値（Valure）を標準誤差（Std Error）で割ったものです。これら t-値は、パラメータの確かさの度合いを表しています。カーブの上限は、最大の確実さを持っています。カーブの勾配あるいは幅では、確実さはもっもと低くなっています。薬理学的データとしては、標準誤差、信頼区間ともによい値を示しています。

Options メニューで、要約として表示するデータの表示／非表示を切換えることができます。

Xmin から Xmax の関数値範囲は、1E-8 精度のガウス求積法で計算しています。関数と微分の極値にはブレント法を使用しています。1次導関数の最小 X 値は、極値のピークの中心となります。すべての TableCurve 2D の推移関数は、カーブの 50％の X値（X50）を表示します。対称形推移関数の場合は、ピークの中心と X50 が一致します。

Numeri Summary ウィンドウをスクロールしてテーブルの内容をチェックしたら、数式リストで 2つ下（非対称形シグモイド関数）に移動してください。

Rank 3  Eqn 8092  AsymSigR(a,b,c,d,e)

r² Coef Det    	DF Adj r²      	Fit Std Err    	F-value
0.9992908869   	0.9990939110   	0.5622571952   	6693.7582600

 Parm  	Value        	Std Error    	t-value      	99% Confidence Limits     	P>|t|
a    	79.63171966  	0.299006021  	266.3214590  	78.77628301  	80.48715630  	0.00000
b    	-46.6811462  	0.415867559  	-112.250031  	-47.8709161  	-45.4913764  	0.00000
c    	10.02303344  	0.057336511  	174.8106630  	9.858997440  	10.18706945  	0.00000
d    	1.025013498  	0.110559341  	9.271161411  	0.708710462  	1.341316534  	0.00000
e    	0.299893428  	0.046812693  	6.406241693  	0.165965378  	0.433821479  	0.00000

t-値は小さく、信頼区間も広い上、パラメータの決定も同じ傾向を示していることに注意して下さい。ただし、幅は 2項となっており、そのどちらも確しかさが高くありません。追加パラメータと F 統計量を大きくするには、全体のフィッティングが非常によくなるようなものでなければなりません。この例では、5パラメータモデルを使用するメリットは何もありません。

Close the Numeric Summary ウィンドウを閉じ、最上位の関数に戻って下さい。

16. データの要約

Data オプションを開くと、ポイント毎のデータの要約すなわち残差、信頼区間、予測区間を表示してくれます。

Preview Curve-Fit ウィンドウのコントロールパネルにある Data ボタンをクリックします。再度このボタンをクリックすると、ウィンドウが閉じます。

17. 第1次導関数と累積分布の表示

Preview Curve-Fit ウィンドウのコントロールパネルにある Toggle First Derivative on Y2 Axis ボタンをクリックします。

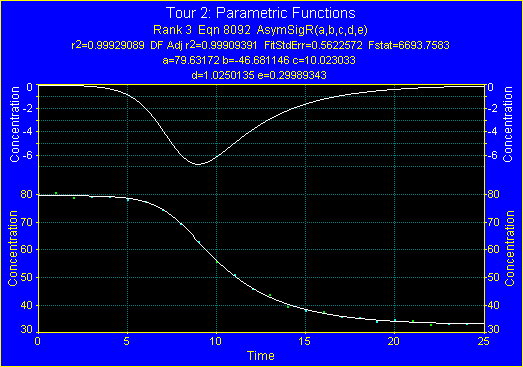
これは、極値の累積分布の導関数であるため、反転したピーク形状となります。

18. ポイント毎の残差

Preview Curve-Fit ウィンドウのコントロールパネルにある Toggle Residuals on Y2 Axis ボタンをクリックすると、残差とフィッティングの両方を表示してくれます。
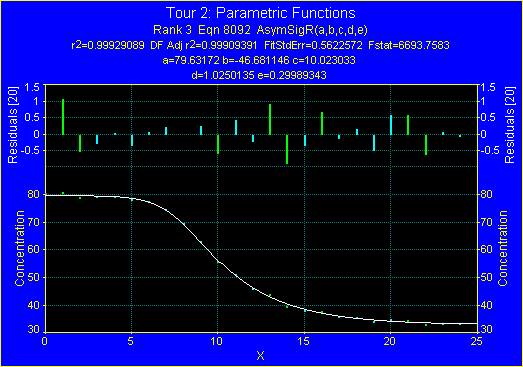
ウィンドウを閉じる場合も、このボタンをクリックします。
OK ボタンをクリックして、Review Curve-Fit ウィンドウを閉じます。

19. ユーザー定義関数

いま私たちを、クロマトグラフィのデータが、人間の血液中から薬が消えてゆくこの曲線と同じ特性をもつかどうか、調べている薬理学者であると仮定しましょう。薬はしばしば、その分子構造がもっているクロマトグラフィのメカニズムと類似した特性を持っています。

EMG（Exponentially-Modified Gaussian）法と HVL（Haarhoff-VanderLinde）法は、クロマトグラフィでよく使用されるフィッティング手法です。TableCurve 2D のユーザー定義関数（UDF）として、この 2つのモデルを使用してみましょう。TableCurve 2D は、UDF をそれぞれ 1つのファイルに保存し、さらに複数のファイルをライブラリとして保存することができます。そこで Cumulative EMG と Cumulative HVL モデルを含んだライブラリを読み込みましょう。

TableCurve は、標準で Cumulative EMG モデルを用意していますが、ここでは UDF の使用法を説明するためにライブラリを読み込みます。

Process｜User Functions メニューコマンドまたはボタンを選択して下さい。User Defined Function ウィンドウで Read UDF Library ボタンをクリックし、SAMPLE01.UDL ファイルを選択し OK ボタンを押して下さい。

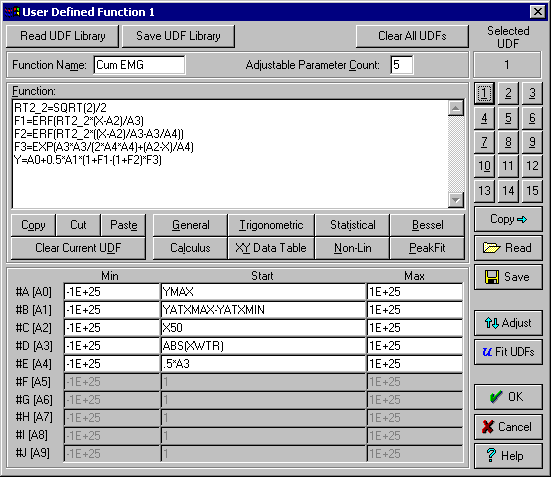
ユーザー定義関数は、A0, A1, A2 などをパラメータ設定に使用します。Cumulative EMG 関数は、5パラメータのやや複雑なモデルです。パラメータの式を使って、XY データ範囲にユーザー定義関数を適用します。ユーザー定義関数には、いくつかのルールがあります。標準の関数を実行するときと同じくらい早く数式を見つけ出すために使用されます。

20. UDF Auto Adjust

非線形フィッティングがうまく収束するように、Adjust ボタンをクリックしてパラメータの調整を行います。さらに個々のパラメータを調整するのではなく、Find & Update ボタンをクリックすると、自動的に最適な推定値を探し出してくれます。
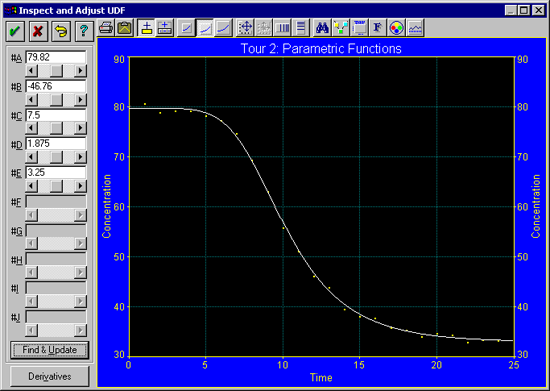
よい推定値が見つかったら OK ボタンを押し、数式を置換えるダイアログ（Replace Formulas with Changed Numeric Values）にはいと答えて下さい。

ユーザー定義関数をディスクに保存しない限り、この設定は一時的なものです。

User Defined Function ウィンドウ右上にある 1〜15 の数字のキーパッドは、適用可能なユーザー定義関数 15個の中からどれを使用するか選択するためのセレクタです。Cumulative HVL 関数は、このライブラリの 2番に保存されています。
数字キーの 2 番をクリックして、ユーザー定義関数を切換えて下さい。

Cumulative HVL 関数も 5つのパラメータを持っています。
再度、Adjust ボタンと Find & Update ボタンをクリックして、自動的に最適な推定値を求めて下さい。
よい推定値が見つかったら OK ボタンを押し、数式を置換えるダイアログ（Replace Formulas with Changed Numeric Values）にはいと答えて下さい。
User Defined Function ウィンドウにある OK ボタンをクリックすると、メインウィンドウに戻ります。
Process｜Curve-Fit Transition Functions メニューコマンドまたはボタンを選択します。
ボタンをクリックして、フィッティングをやり直します。
フィッティングが終了したら、Graph Start ボタンを押して下さい。

アクティブなすべてのユーザー定義関数が、フィッティングに使用されます。したがって、現在の数式リストには 12 の関数が表示されているはずです。

最初のユーザー定義 Cumulative EMG 関数は、標準の EMG Cumulative (数式番号 8189) と同等だと述べましたが、それを確認することができます。したがって、問題は 5パラメータの Cumulative HVL 関数がシンプルな 4パラメータのモデルよりもよい F 統計量を実現できるか、ということになります。

注意：ユーザー定義の Cumulative EMG が、標準関数とまったく同じ結果を生み出すわけではありません。また F 統計量から見て、Cumulative HVL 関数は決してよいとはいえないでしょう。
Review Curve-Fit ウィンドウの OK ボタンをクリックして、フィッティングを終了して下さい。File｜Exit メニューコマンドまたはメインウィンドウの閉じるボタンを押してプログラムを終了します。

この生理学的サンプルデータを使って、いくつかのよいモデルを見つけ出すことができました。シンプルな 4パラメータの ExtValCum(a,b,c,d) と LgstcDoseRsp(a,b,c,d) 関数が、明らかによいモデルです。この種のデータは、伝統的に Logistic Dose Response モデルが適用されます。