ヒューリンクステクニカルサポート
TableCurve 2D/3D サポート情報 TableCurve 2D / 3D 製品ページ
更新日： 14/04/15

3. ノンパラメトリック補間

ここでは TableCurve 2D によるノンパラメトリック推定（補間）について説明します。

世の中にはパラメトリックモデルでも、データの特性をうまく説明できない事象がよくあります。こうした場合、高次の多項式またはは有理関数を使っても、うまくいきません。そのようなケースでは、ノンパラメトリックな手法を用いて補間を行います。

非常によいパラメトリックモデルでも、残差に何らかの特徴的な傾向が見られるときは、データの特性を十分に表現はしていません。ここでは、TableCurve2D がもつノンパラメトリック推定を使って、よいモデルを見つけてみます。

ところで TableCurve 2D は、X 値の間隔が一定であることを前提とするアルゴリズムも備えています。これはカーブフィッティングには不向きですが、フーリエ解析や固有値解析には向いています。等間隔の X 値は、AR（自己回帰）推定や Savitzky-Golay 法でも必要です。データの X 値が等間隔でないときは、補間に基づいてパラメトリックモデルを構築するよりも、ノンパラメトリック補間を使用した方が、より簡単になります。

  1. 平滑化、推定、予測とは
  2. パラメトリックとノンパラメトリック
  3. スムージング／ノイズ除去とアナログ推定
  4. 推定の手法
  5. ノンパラメトリック補間
  6. パラメトリックフィッティング
  7. スプライン推定

 

1. 平滑化、推定、予測とは (Smoothing, Estimation, and Prediction)

TableCurve 2D の平滑化（スムージングあるいはノイズ除去）は、X 値（元データと同じ）において、変化を滑らかにした Y 値（元データと異なる）を返してくれるアルゴリズを意味します。補間や外挿は行わず、連続的な推定を行う機能はもっていません。

予測 (Prediction) は、等間隔の X 値を持つデータに対して実行され、時系列データの予測と同じように、データの両端あるいは片端に離散した X 推定値を生成します。補間は行われず、同じ X 値間隔をもつ任意の数のデータを追加することができますが、連続関数はもちません。

推定（Estimation）は一方、Y 値を計算するための X 値は、ユーザーが任意に設定できます。補間が行え、フィッティング近似関数を用いて外挿や予測が可能です（あまりよい結果が得られませんが）。連続関数あるいはそれに類する手段を用いて、計算を行います。

 

2. パラメトリックとノンパラメトリック

TableCurve 2D では、パラメトリックとは現象の特性を示すパラメータセットを見つけ出すことを意味します。ノンパラメトリックでは、パラメータセットがあったとしても、それは中間的なものとして扱われ、ユーザーには提示されません。

厳密に言えば、何らかのパラメータセットを使って計算しているという意味では、すべての手法はパラメトリックです。関数の係数の代わりにフーリエ係数、Savitzky-Golay あるいは Kaiser Bessel フィルタの係数、固有ベクトルや固有値、局所的な回帰係数、スプライン係数などを用いています。

 

3. スムージング／ノイズ除去とアナログ推定

Filter メニューでは、スムージング、ノイズ除去、成分の分離などにより、元データを変える手法が提供されます。これらのオプションを使ったとき、X 値は元データと同じものが返されます。

Estimate メニューには、TableCurve 2D のもつすべてのノンパラメトリック推定および AR（自己回帰）予測のための手法が用意されています。ここでは、X 値は通常元の値から変更され、自己回帰の場合はさらに拡張されて、補間の境界や推定の際の密度として使用されます。

ここでは、Estimate メニューの中で補間が可能なものだけを紹介します。

 

4. 推定の手法

Spline Estimation コマンドでは、重要な 8種類のスプライン推定法を用意しています。このうちの 5つは、平滑化スプラインすなわち交差検証キュービック法、NURBS、最小2乗法 B スプラインです。

Fourier Estimation コマンドは、フーリエ成分から導き出した補間と平滑化が可能なフーリエフィルタです。

Smoothed Data Spline Estimation コマンドは、自動平滑化および B スプライン推定の機能をもっています。ただし、これらは平滑化スプラインではなく、平滑化前のデータに対してフィッティングや補間を行うための B スプラインです。

Local Regression Spline Estimation コマンドは、Loess アルゴリズム (高次なものを含む) と補間が行えます。

Savitzky-Golay Spline Estimation コマンドは、制約付きキュービック（3次）スプライン補間が行えます。この手法は、導関数の推定に最適化されています。

 

5. ノンパラメトリック補間

ノンパラメトリック補間に有用な手法を見ていきましょう。これらのアルゴリズムは平滑化のために使用することもできますが、ここでは基本的に補間を行います。

  1. TableCurve 2D を起動して下さい。

  2. File｜Import メニューコマンドまたはメインツールバーにある Import ボタン を選択して下さい。Excel [xls] ファイル形式が表示されないと場合は、ファイルの種類ドロップダウンリストをクリックして、Excel [xls] 形式を選択して下さい。SAMPLE.XLS ファイルを開きます。

  3. X-values として (10)Prediction!C: Prediction 40dB Time のラベルが付けられた列を選択します。Y-valuse には、 (10)Prediction!D: SN40dB を選択します。Import Preview のチェックボックスを ON にすると、インポートするデータのグラフが表示されます。


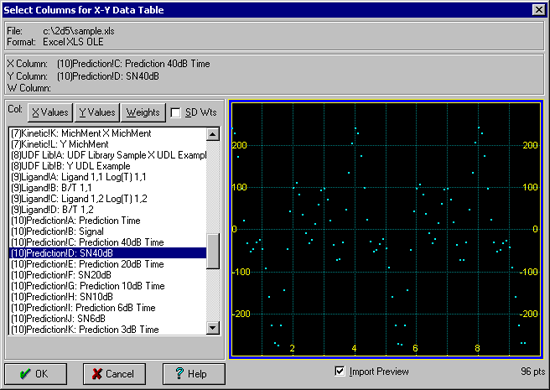
    注意：最初に選択した 2列は、自動的に XY データとして読み込まれます。リストの列名をダブルクリックするだけで、選択することができます。XY 変数の列は、重み Weights の列を選択するのと同じように、変更することができます。Weights の列は、複数の Y 列データの標準偏差として使用することもできます。

  4. 選択が終わったら、OK ボタンを押します。データ列名を編集するダイアログ現れますので、もう一度 OK ボタンを押して下さい。

    このデータセットには、3つの正弦波と 1% のガウスノイズが乗っています。

 

6. パラメトリックフィッティング

  1. Process｜Curve Fit Poly/Ratl Equations メニューコマンドまたは ボタンをクリックして下さい。
  2. フィッティングが終わったら、表示されたダイアログの Graph Start ボタンをクリックします。

    OK ボタンを押した場合は、Review｜Graph Start メニューコマンドまたは ボタンをクリックして下さい。何もしないで10秒が過ぎると、自動的に Review Curve-Fit ウィンドウに切り替わります。

  3. Review Curve-Fit ウィンドウの List メニューまたは Equation リストの Sort メニューから Sort by r2 を選択して下さい。


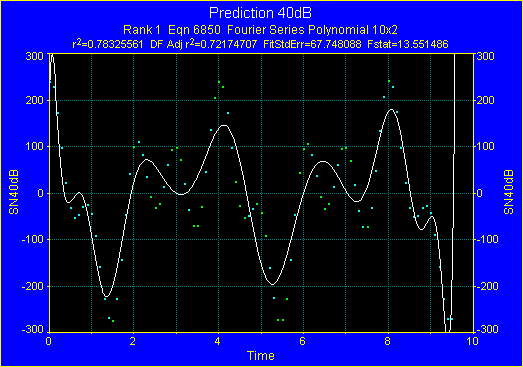
    もっともよい関数は 21 パラメータのフーリエ級数多項式ですが、局所的に最大値、最小値をうまく当て嵌めることができません。こうした場合に、ノンパラメトリックな手法が有効となります。

  4. OK ボタン をクリックして、Review Curve-Fit ウィンドウを閉じます。

 

7. スプライン推定

  1. Estimate｜Spline Estimation メニューコマンドまたはツールバーの ボタンを選択し、Algorithm セクションにある Cubic のオプションをチェックして下さい。

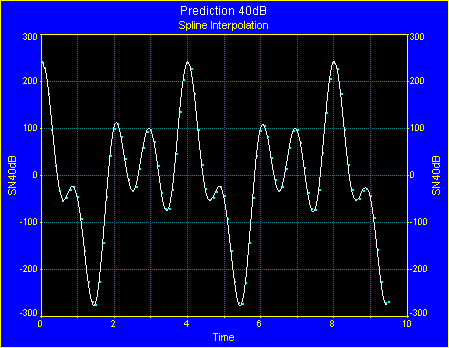
    基本的なキュービックスプラインでも、とてもよいデータの補間ができました。

TableCurve 2D には、様々なスプラインのアルゴリズムが用意されています。もっとも基本的なのがキュービックスプラインです。これらは、滑らかな1次導関数と（滑らかではないが）連続した 2次導関数を生成します。

 

B-スプラインを使ったオプションは 4つあり、そのうちの 3つは過剰決定系の最小2乗法フィッティングです。

NURBS というアルゴリズムもあります。

これらのアルゴリズムを使えば、ほとんどの推定が可能ですが、TableCurve はさらに 4つの推定手法を用意しています。これまでに紹介した方法でよい平滑化が得られない場合、新たな手法のどれかを使用して下さい。

 

Smoothed Data Spline Estimation は、TableCurve 2D の自動平滑化と B-スプライン推定の機能を併せ持っています。データは事前に平滑化され、B-スプラインフィッティングが行われます。固有振動による方法は、データがもつ傾向を損なわずに、よくノイズを除去することができます。

Local Regression Spline Estimation は、Loess 平滑化アルゴリズムより優れた結果が出ます。Loess 法は、ノイズが非常に大きく、データの傾向が見て取れないような場合に、大変有効です。

Savitzky-Golay Spline Estimation は、大変良好な Savitzky-Golay 平滑化アルゴリズムと、制約付きキュービックスプライン補間を実行します。導関数を推定するときは、この方法が適しています。

Fourier Estimation は、フーリエ成分から導かれた補間と平滑化を用いた周波数フィルタです。

平滑化の詳細は、ノイズ除去 ("Noise Redction") のチュートリアルを参照して下さい。

  1. Spline Estimation のウィンドウを ボタンをクリックして終了して下さい。

  2. Estimate｜Fourier Estimation メニューコマンドまたはツールバーの ボタンを選択して下さい。

  3. Remove Trend チェックボックスは OFF にしておいて下さい。Window セクションのドロップダウンリストは None、Output Data セクションのドロップダウンリストは Function、n には 1024 を入力して下さい。

  4. 下のグラフで、マウスを使って x=8.5 から x=9.5 の範囲をズームインして下さい。

  5. 下のグラフのツールバーにある Modify Point Format ボタン 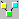をクリックして下さい。Y2 Axis ラジオボタンを ON にし、Size を 4 に変更して OK ボタンを押します。


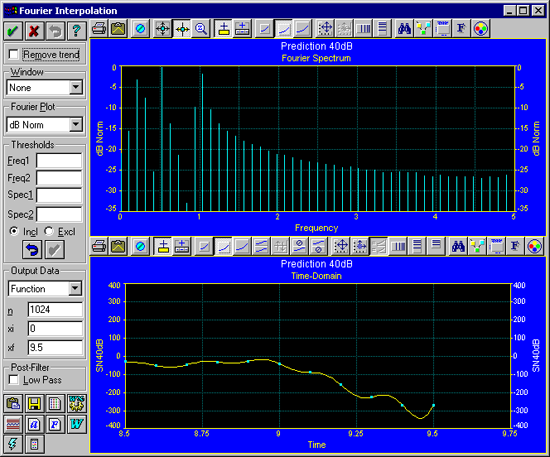
    最後のいくつかのデータポイント間に振動があることに注意して下さい。

  6. Remove Trend チェックボックスを ON にし、Window セクションのするスクロールダウンリストで cs3 BHarris 3 を選択して下さい。


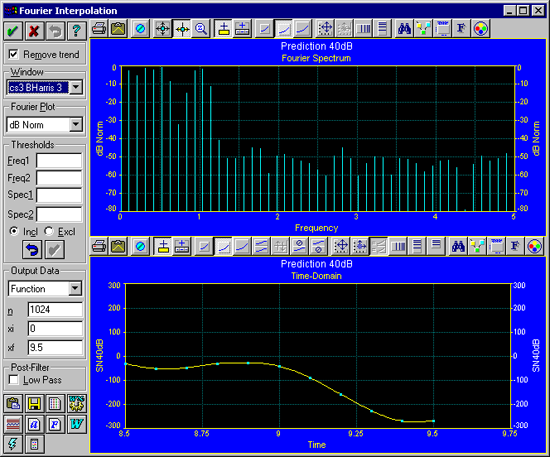
    どちらのフーリエ分解も入力データに対してよい結果を示していますが、補間に関しては異なっています。データの最後の部分の振動は、もう見られません。

    このケースのように、信号とノイズとの閾値がはっきりしている場合は、ノイズを除去するのは簡単です。

  7. Thresholds セクションの Spec1 に -40 を入力し、Excl のラジオボタンを ON にして下さい。


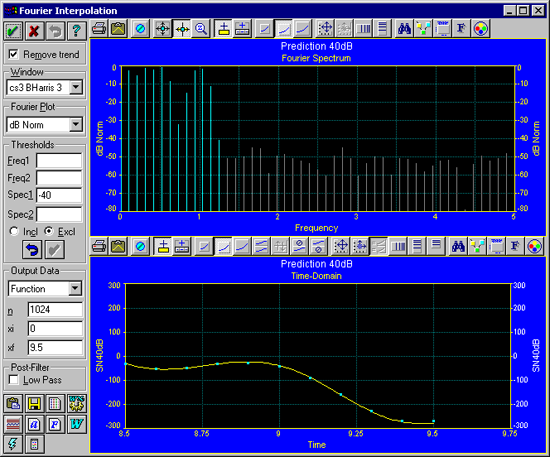
    ノイズを除去すると推定が向上しますが、補間は実行されていません。フーリエモデルは、これでデータポイントの上を正確に通過することはなくなります。

  8. Cancel ボタン をクリックして、フーリエ推定を終了して下さい。