 |
| サイトマップ | |
|
 |
| サイトマップ | |
|
Ricketts と Head によって考案された5パラメータのロジスティック関数 (5PL) は、2つの勾配パラメータ Slope1 と Slope2 を使用して非対称の用量-応答曲線 (dose-response curves) を説明するものです (勾配パラメータが1つの4パラメータのロジスティック関数は対称となります)。
5PL の方程式を以下に示します:
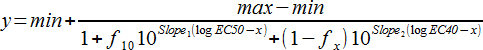
![]()
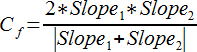
パラメータは以下のとおりです:
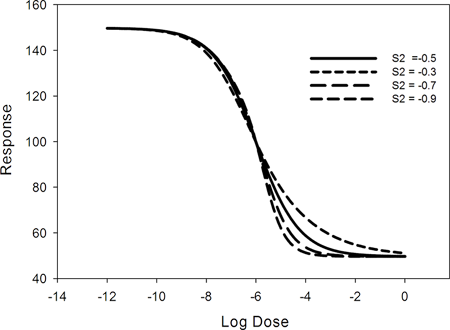
用量-応答曲線は2つの勾配が負の場合、 x の増加に従って減少します。x = logEC50 における曲線の勾配は、(max – min)*(Slope1 + Slope2)*ln(10)/8 であらわされ、2つの勾配の和に比例します。Ricketts と Head は、2つのパラメータが下図に示すように曲線の上部と下部の曲率に関係することから、これらを曲率パラメータ (curvature parameters) と呼びます。
 |
SigmaPlot には、この方程式が予め装備されていますが、初期パラメータを推定する適切な関数は用意されていません。Ricketts と Head の論文 (1) の付記にある血圧と心拍数に関する実験データを使用し、この方程式をあてはめてみました。まずはじめに、単一曲線のあてはめを実行し、その後、あてはめを500回試行するダイナミックフィットを実行しました。ダイナミックフィットは、推定される大域的最小値 (global minimum) と局所的最小値 (local minimum) を求めます。単純な初期パラメータ推定関数を使用した単一のあてはめでは、局所的な最小値が求まりましたが、これは推定する大域的最小値ではありません。以下に示すダイナミックフィットプロファイルは、ダイナミックフィットの結果に関する残差平方和の最小の値から最大の値までを対数であらわしています。
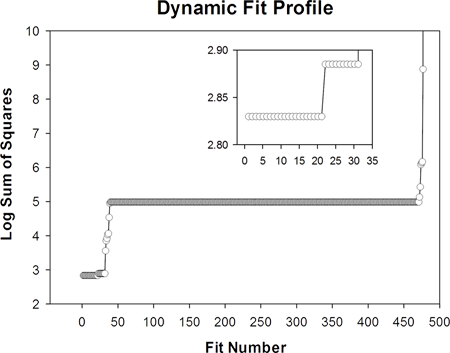 |
挿入したグラフの2段階の水準は、推定される大域的最小値と最初の局所的最小値を示します。結果の大部分 (あてはめ番号 30 から 475 の間) は、y データの平均値における水平方向の直線のあてはめに対応します。挿入したグラフの平方和の値に対応するデータと2つのあてはめの解を以下に示します。
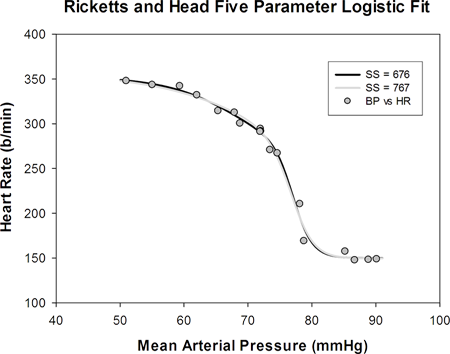 |
表示される2つの解のパラメータの値をそれぞれ以下に示します:
| Solution | RSS | min | max | logEC50 | Slope1 | Slope2 |
|---|---|---|---|---|---|---|
| global minimum | 676 | 150.3 | 353.6 | 75.5 | -0.066 | -0.251 |
| local minimum | 767 | 150.0 | 355.6 | 75.2 | -0.279 | -0.019 |
Slope1 と Slope2 の値の大きさが、2つの解でどう異なっているかに注目します。Slope1 は、大域的最小値 (global minimum) において大きさ (絶対値) が最小となり、局所的最小値 (local minimum) においては大きさが最大となっています。これは、残差平方和の値が2つの解で異なっているため、指数和の指数内のパラメータに関して生じる (指数の2つの項を交換する) 人為的な「スイッチ」ではありません。この挙動は、以下の事例に示すように 5PL 方程式に特有の性質であると考えられます。
この 5PL 方程式で、シミュレーションされたデータを更に調査しました。データに対してひとつのあてはめが行われると、その後、あてはめを500回試行するダイナミックフィットが実行されます。ダイナミックフィットプロファイルは推定される大域的最小値と3つの局所的最小値をあらわすグラフを挿入します。
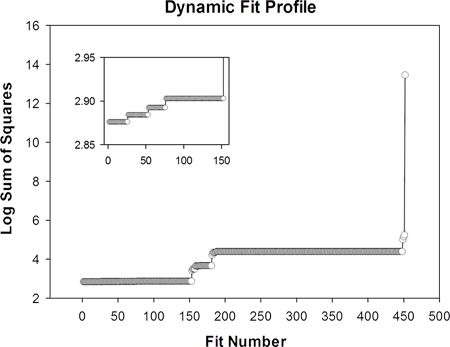 |
データとこれら4つの解のあてはめ曲線を以下に示します。
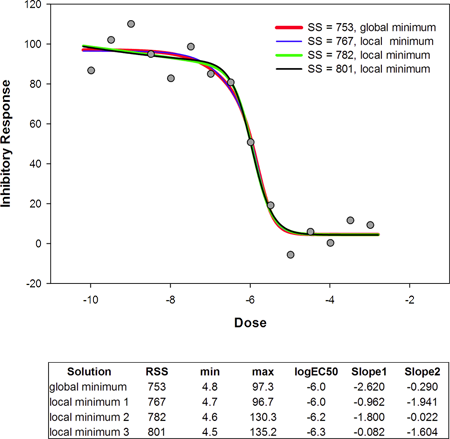 |
互いに殆ど一致している組が2つ合計4つのあてはめ解が表示されます。最初の組は、x (dose) の値が小さいところでは勾配がほとんどゼロですが、もう一つの組はそうではありません。以下にあてはめに関するパラメータの値を示します:
| Solution | RSS | min | max | logEC50 | Slope1 | Slope2 |
|---|---|---|---|---|---|---|
| global minimum | 753 | 4.8 | 97.3 | -6.0 | -2.620 | -0.290 |
| local minimum 1 | 767 | 4.7 | 96.7 | -6.0 | -0.962 | -1.941 |
| local minimum 2 | 782 | 4.6 | 130.3 | -6.2 | -1.800 | -0.022 |
| local minimum 3 | 801 | 4.5 | 135.2 | -6.3 | -0.082 | -1.604 |
最初の組 (global minimum と local minimum 1) と2つめの組 (local minimum 2 と local minimum 3) において、今回も、勾配の大小が Slope1 と Slope2 の間で入れ替わっています。前回も触れましたが、x = logEC50 における 5PL 曲線の勾配は、2つの勾配の和に比例します。最初の解の組における勾配の合計 Slope 1 + Slope 2 はそれぞれ –2.90 と -2.90 であり、2つの曲線は互いに良く似ていることを示します。2つめの組においてもこの和は –1.82 と –1.68 となり、こちらも近い値を示しています。
この事例が示すのは以下のことです:
非線形カーブフィットが残差平方和の最小値に収束しない場合があります。その場合は以下のようなメッセージが表示されます:
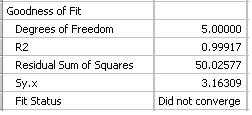
または
このような状況は、データに対して方程式が複雑すぎる場合に多く発生します。例えば、飽和結合データに1サイトおよび2サイトの方程式のあてはめを行い、そのあてはめの結果を比較してどちらが良い方程式かを比較するような場合です。そもそもデータに1サイトの性質しかなければ、2サイトの方程式で収束するかどうかは分かりません。2サイトの方程式が収束しなければ、1サイトの方程式を比較に使用して、どちらがいいかを判断することはできません。従って、次のように行き詰ってしまいます。「1サイト結合パラメータは・・・でしたが、2サイトのモデルは収束しませんでした」 (2) となり、データが2サイトの方程式をサポートしないことが視覚的に明らかであるにもかかわらず、このことを簡単に主張することができず、1サイトとのあてはめを比較することができません。ダイナミックフィットは、収束しないものに対しては何の結果も表示しません。従って、何らかの結果が得られたとすれば、それらは収束したことになります。しかし、下位桁あふれ (underflows) にってもたらされる無効なあてはめにおいて、ダイナミックフィットの結果で有効なあてはめが存在することがあり、その場合は、1サイトと2サイトのあてはめ結果を統計的に比較することができることもある点に注意する必要があります。
以下に示すのは、SigmaPlot の2サイト結合の方程式のあてはめを1度行い収束しなかった飽和結合の事例です。1回目に設定したパラメータの初期推定値がたまたま悪かったために、このデータセットで収束解を得ることができなかったのです。この種の挙動は、あらゆるカーブフィットで発生する可能性があります。ダイナミックフィットならこれを (多くの異なる "最大限の距離をもつ" パラメータの開始点のセットを使って) 実行し、殆どの解が収束します。以下に残差平方和の値が最も小さい 50.03 で収束したあてはめを示します:
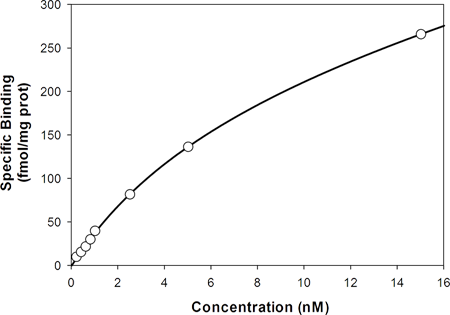 |
従って、ダイナミックフィットは、単一のあてはめで解が収束しない場合の回避策として使用することができます。
2サイトのあてはめを収束できたので、1サイトのあてはめと比較することができるようになります。
以下の表は1サイトおよび2サイトのあてはめの両方について残差平方和 (RSS)、赤池情報量基準 (AICc)、および、2つのモデルの正しさのの確率を示したものです。
| Equation | RSS | AICc | Delta AICc | Probability (%) |
|---|---|---|---|---|
| one-site | 67.3 | 28.9 | 0.0 | 99.97 |
| two-site | 50.0 | 45.4 | 16.5 | 0.03 |
予想されるとおり2サイトのあてはめの方が残差平方和は低くなっています。しかし、1サイトのあてはめの正しさの確率が 99.7% と圧倒的であるのに、赤池の AICc 値は2サイトの方が1サイトより大幅に高くなっています。
ダイナミックフィットレポートの2つ目のセクション “Summary of Fit Results” は、あてはめ結果の種類別の要約を示します。検出されるのは以下の状態で、あてはめ総数に対するパーセンテージで表現されます。
レポートのこのセクションは、調査する特定の問題の難しさの特性を把握するのに利用できます。例えば、合理的なデータセットに対して単純な指数あてはめのダイナミックフィットを 200 回実行すると以下のようになります。
Summary of Fit Results: Converged 100.0% Singular Solutions 0.5%
200回のあてはめが全て収束し、そうち1つが特異解でした。単純なこの問題では、ダイナミックフィットが必要なかったことは明らかです。事例5のように非常に複雑な問題でも、あてはめ結果のサマリーで失敗が少ないことをご確認ください。
これとは反対に、NIST ウェブサイトで提供されるデータに対する Bennett5 方程式のあてはめで、開始するパラメータ値に難易度の高いセットを使用すると、以下のような結果になります:
Summary of Fit Results: Converged 44.5% Singular Solutions 6.0% Ill-Conditioned Solutions 31.5% Evaluation Failure 0.5% Iterations Exceeding 2000 33.0% Inner-Loop Failures 22.0%
この例は、ダイナミックフィットで出力される結果のすべての状態を具体的に示したものです。200回のあてはめのうち、44.5% しか収束していません。全体の 6% が特異解で、31.5% が状態の悪い解です。つまり、37.5% は「クオリティの低い」あてはめということになります。すなわち、無効な推定値や、非常に変動性の高いパラメータ推定値もこのケースに含まれていることになります。したがって、有効なパラメータ推定は 200回のあてはめのうち 44.5% - 37.5% = 7% しか得られなかったことになります。
収束しなかった 55.5 % のうち、0.5% (1 fit) は評価に失敗したもの (ゼロ除算、指数オーバーフロー、負の数の平方根など)、33% が指定した最大反復回数 (この事例では 2000 回) を超えたもの、22% が内部ループに失敗したもの (Marquardt-Levenberg アルゴリズムの内部ループの反復回数が 50以上になったもの) となります。
以上でこれは困難なカーブフィッティング問題であることが明らかになりました。また、パラメータに難易度の高い初期値を使うことで、使用する初期開始値がどれだけ重要であるかが分かりました。
ダイナミックフィットは、適切なパラメータの初期推定値の決定にも利用することができます。これは、初期パラメータ推定関数、または、パラメータの適切な初期値の生成が困難な複雑な方程式で非常に役立ちます。例えば、Bates と Watts による動粘性率 (kinematic viscosity) の問題 (3) などがその一例です。
以下に温度と圧力の関数として測定された動粘性率のデータを示します:
 |
このデータに対するあてはめの方程式は以下のとおりです。
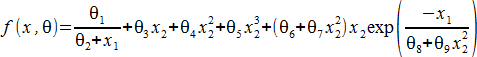
ここで、f は ln(粘度)、x1 は温度、 x2 は圧力をあらわします。
各温度について、データは圧力 (x2) の変化と線形の挙動を示しています。温度ゼロにおける圧力データの勾配は、約 1.5 です。x1 = 0 の方程式から、その勾配はおよそ θ3 + θ6 となります (x2 における高次の項はデータがほぼ線形であることから小さな補正であるとみなします)。これにより、おおよその見積り θ3 + θ6= 1.5 が得られます。この和を分割する方法を知らないので、初期推定値として θ3= 1.0 と θ6= 1.0 を使用することにします (明確にするため端数を切り上げます)。ダイナミックフィットでは、パラメータ毎に数値の範囲を指定する必要があります。ここでは、経験則に従って、パラメータ範囲の下限と上限をそのパラメータ値のプラスマイナス2倍に設定します。従って、 θ3 と θ6 の範囲は [-1, 3] となります。上記グラフからデータは圧力に対して真の線形でなく、幾分かの曲率があることがわかります。θ4 と θ5 の項がこの説明に役立ちます。この曲率は、あまり急激ではないので、θ4 と θ5 の初期推定値には θ3 の 1/10 と 1/100 をそれぞれ使用することにします。これら2つのパラメータの符号はどうなるか分からないので、 |θ4| = 0.1 と |θ5| = 0.01 とします。また、これらの範囲は、ゼロに対してプラスマイナス2倍の対称にします。従って、これらの範囲は、θ4 = [-0.2, 0.2] と θ5 = [-0.02, 0.02] となります。
残りのパラメータは、温度との挙動、および、温度と圧力との複合挙動を特徴づけるものです。グラフの圧力ゼロ x1 = 0 のデータを調べれば、 θ1 と θ2 の推定値を求めることができます。関数 θ1/(θ2 + x1) は、温度 (x1) の増加に従って減少する双曲線関数です。x1 = θ2 のとき、この関数は元の値の半分に減少します。98.9 より大きい温度では、圧力ゼロのデータは、初期値 5.0 以上から 2.5 未満に減少します。従って、大まかな初期推定値として θ2 = 100 を使用することにします。ln(粘度) は、温度と圧力がゼロのとき約 5.0 なので、θ1/θ2 = 5.0 を使用して、おおよその初期推定値 θ1 = (5.0)*(100) = 500 を得ることができます。これにより、 θ1 と θ2 の範囲として、それぞれ、 [-500, 1500] と [-100, 300] を得ることができます。
結合項の温度パラメータ θ8 は何になるかは分からないので、別の双曲線関数の温度パラメータ θ2 = 100 とほぼ同じであると推定します。従って、その範囲は θ8 = [-100, 300] となります。残りの2つのパラメータ θ7 と θ9 は、小さな補正であると考えられるので、他のパラメータの合計の 1/10 とし、また、符号についても分からないので、ゼロに対して対称の範囲になるようにします。従って、θ7 = 0.1*θ6 すなわち θ7 = 0.1 となり、同様に、 θ9 = 0.1*θ8 すなわち θ9 = 10 となり、対応する範囲はそれぞれ、 θ7 = [-0.2, 0.2] および θ9 = [-20, 20] となります。
以上をまとめると、パラメータのおおまかな初期推定値は以下のようになります:
これらの範囲をダイナミックフィットのダイアログに入力すると、最大反復数 200 を使用して、500 のあてはめが得られます。推定される大域的最小値は、500 のあてはめのうち 14% 見つかりました。従って、初期パラメータを推定する代わりにダイナミックフィットを使用する技法が成功したことになります。
SigmaPlot によって求められた解は、Bates と Watts が求めたのと基本的に同じです。SigmaPlot で得た解は、残差平方和がやや低くなっています (SigmaPlot の 0.08738 に対して Bates と Watts は 0.08996) 。この結果の違いは、2つのプログラムの収束の許容値の違いによって生じたものと考えられます。以下にダイナミックフィットプロファイルのグラフを示します。
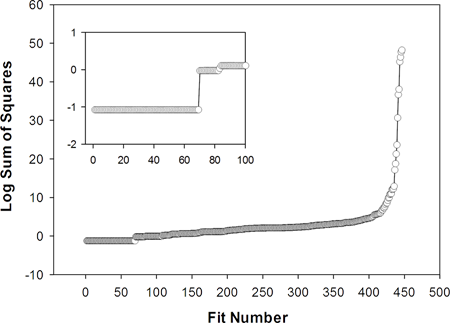 |
挿入されたグラフは、最初のステップレベルにおける 69 のあてはめ解が推定される大域的最小値に収束することを示します。あてはめ結果のサマリーレポートは以下のようになります:
Summary of Fit Results: Converged 89.2% Singular Solutions 31.4% Ill-Conditioned Solutions 21.4% Evaluation Failure 0.4% Iterations Exceeding 200 10.0% Inner-Loop Failures 0.4%
この結果は、約 90% のあてはめが収束に至り、そのうち約 35% は良い状態だったことを示します (89.2 – (31.4 + 21.4) = 36.4)。また、失敗についても比較的少ない数で済んでいます。この方程式はパラメータが9つある複雑なものですが、データの品質はダイナミックフィットで良い結果を得る程度の水準にあります。上記グラフの温度別のプロットそれぞれにあてはめ曲線を生成する簡単なトランスフォームを記述し、表示したのが以下の図です。このあてはめは、残差平方和の小ささから期待するより非常に良いものになっています。
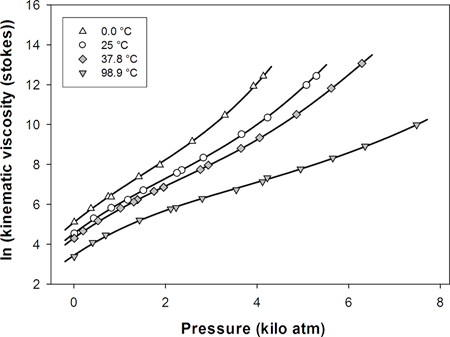 |
大気圧データ内に存在が知られている3つの周期の特性を、正弦関数の和をあてはめて以下に示します (4)。
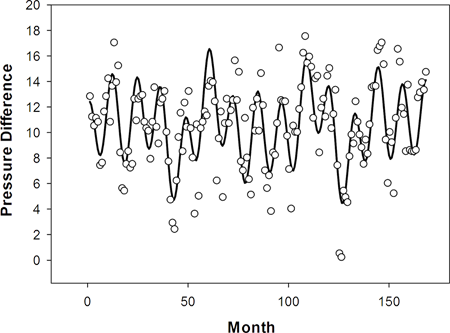 |
SigmaPlot は、参考文献 (4) の記載にあるように、回帰ウィザードにあるひとつのあてはめを使用して、推定される大域的最小値を求めます。データに対する正弦関数の和のあてはめは、多くのあてはめ解において局所的最小値になることが知られています。従って、確たる証拠がないのに、その解が最適解であることをどうやって知ることができるでしょうか?その答えには、確証できるものは何もありません。
しかし、ダイナミックフィットを使えば、それが最適解であるという確信を得ることができます。正弦関数の和のダイナミックフィットは以下のとおりです。
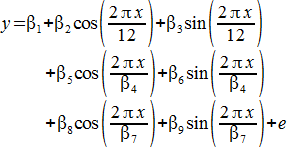
200回のあてはめと、参考文献 (4) にリストされたもっとも困難な開始パラメータ値を使用して実行しました。以下の図は、その結果得られたダイナミックフィットプロファイルです。
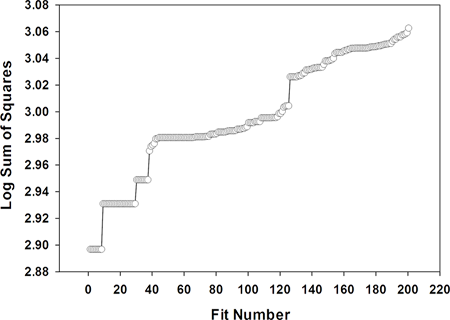 |
上記グラフのはじめの4段階のステップそれぞれにおける複数のあてはめは、局所的最小値が少なくとも3つと、推定される大域的最小値 (平方和の対数値が最も小さいところ) が存在することを意味します。はじめの4つの最小値に関する平方和の対数値は、その範囲が 2.90 から 2.98 までと、ほとんど同じ値をとっています。従って、各解に対応するあてはめ曲線は、比較的近接したものになるだろうと考えることができます。
パラメータが9つあるにもかかわらず、この問題はパラメータの初期値の違いに対して比較的変化を受けないものであることを、このダイナミックフィットのレポートは示しています。すべてのあてはめが収束し、特異解や状態の悪い解の割合はわずかしかありません。
Summary of Fit Results: Converged 100.0% Singular Solutions 3.5% Ill-Conditioned Solutions 4.5%
4つの最小値に対応するあてはめ解を以下の図に示します。
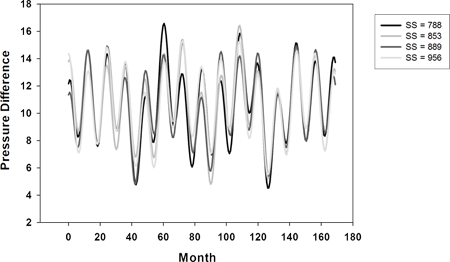 |
これらの解は、残差平方和で検討したとおり、互いに比較的近接したものになっています。これらの解に12か月の周期があることは明白ですが、これに加え、はじめの3つのあてはめには、約26か月と 44か月の2つの周期も存在しています。4つ目のあてはめ解には、85か月の周期 (44か月周期の約2倍) があります。後の解は、正弦関数の和の解に局所的最小値があることによって周期が2倍 (または3倍) になった一例です。
一見したところ、この結果からは最適なあてはめを求めたという確信が持てないように思われます。しかし、ダイナミックフィットを実行したことで、1) 様々な初期パラメータを使って計算を開始して、残差平方和の最も低い値として複数のあてはめ解が求められ、2) すべてのあてはめが収束し、3) 最初のカーブフィットでは求められない一群の相対的な最小値が求められた、ということを通じて、提示されたあてはめが本当に最適解であるという確信を強く抱けるようになります。
12か月周期のパラメータの指定は正当化に必要のないものですが、ダイナミックフィットは12か月周期に対応する10番目のパラメータを使って計算を実行し、推定される大域的最小値と基本的に同じものを求めました。その残差平方和は 773 とやや低く、12か月周期の期間は 11.9 月であると推定されました。
(1) Ricketts, J.H. and Head, G.A. A five-parameter logistic equation for investigating asymmetry of curvature in baroreflex studies. Am. J. Physiol.277 (Regulatory Integrative Comp. Physiol. 46); R441-R454, 1999.
(2) Aymerich, M.S., Alberdi, E.M., Martinez, A. And Becerra, S.P. Evidence for Pigment Epithelium-Derived Factor Receptors in the Neural Retina. Invest. Ophthal. & Visual Science, Vol 42, No. 13, 3287-3293, 2001.
(3) Bates, D.M, and Watts, D.G. Nonlinear Regression Analysis and its Applications. Wiley, New York, 1988, pp 87-89.
(4) The NIST Statistical Reference Datasets for Nonlinear Regression, http://www.itl.nist.gov/div898/strd/nls/nls_main.shtml, dataset ENSO.