データの分析
列の統計量の表示
KaleidaGraph は、データ解析に役立つ 12種類の統計値を表示します。これらの統計量は、データウィンドウの各列について自動的に計算されます。
- データセットの統計量を表示するには:
- 統計量を計算するデータを選択します。データを選択しない場合は、データウィンドウの各列について統計量が計算されます。
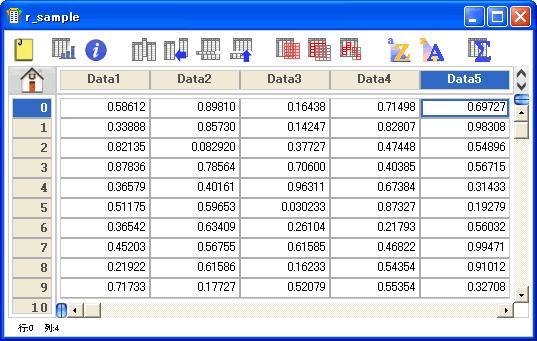
- データウィンドウで機能>統計を選択するかを
 クリックします。統計ダイアログに分割画面が表示され、それぞれの画面の列どうしを比較することができます。 クリックします。統計ダイアログに分割画面が表示され、それぞれの画面の列どうしを比較することができます。
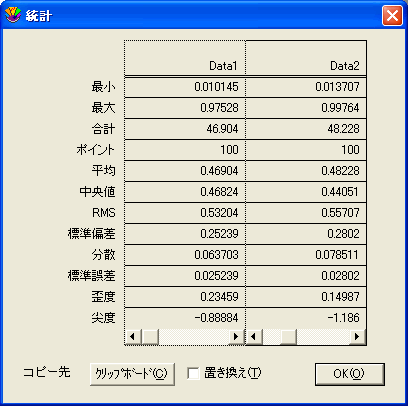
- 統計量をデータ、プロット、またはレイアウトのウィンドウに貼り付けるには、コピー先クリップボードをクリックします。また、置き換えチェックボックスをオンにすると、データのコピー時に各統計値が列に、変数が行に入れ替えられます。
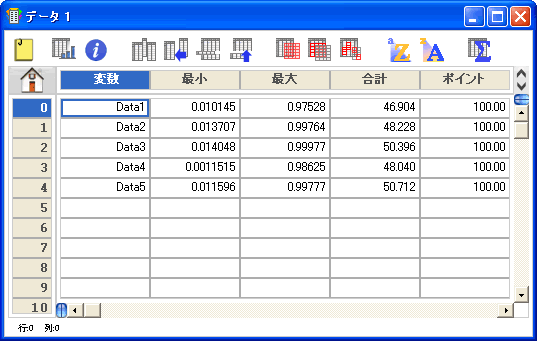
- 統計量の確認、操作が終了したら OK をクリックします。
関連:サマリーコラムプロット
データの階級化
データの階級化では、一定範囲内にあるデータ数がカウントされます。分割されたデータ分布は、3種類のグラフ形式やグラフの注釈用形式にエクスポートすることができます。
データの階級化
- データを分割する変数を持つ、1つ以上の列を選択します。
- 機能>データの階級化を選択して、データの階級化ダイアログを表示します。
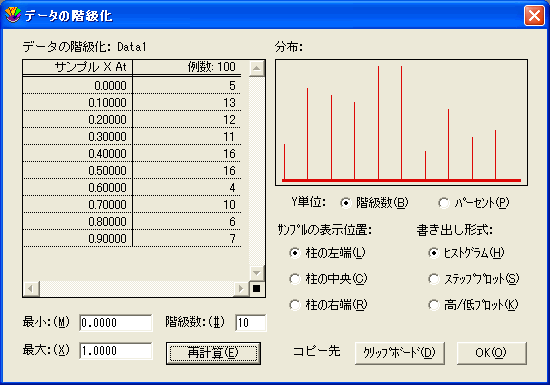
- 最小値 (最小)、最大値 (最大)、分割数 (階級数)、Y軸の単位 (Y単位)、データ数の表示位置 (サンプルの表示位置) を指定して、変数のデータを分割します。最小値 (最小)、最大値 (最大)、または分割数 (階級数) を変更した場合は、再計算をクリックしてデータ数を更新します。
- 作成するグラフの種類 (書き出し形式) として、適切な書き出し形式を選択します。
- クリップボードをクリックします。
- OK をクリックします。
データの階級化ダイアログの結果のペースト
- ファイル>新規作成を選択して、空白のデータウィンドウを作成します。
- 編集>ペーストを選択して、データウィンドウに結果をペーストします。
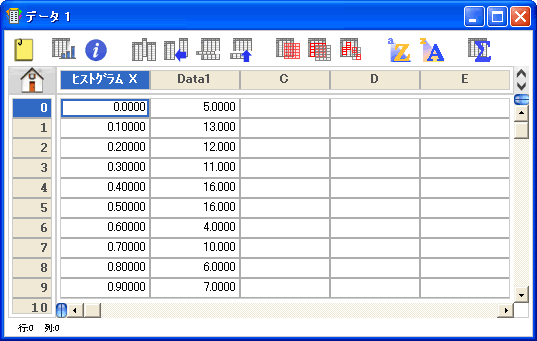
グラフの作成
- ギャラリーメニューからグラフの種類を選択します。
- ヒストグラム-変数が 1つの場合は、ギャラリー>棒グラフ>コラムを選択します。
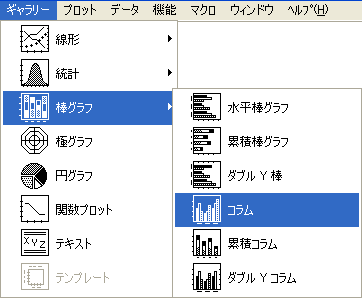
- 変数が複数の場合は、ギャラリー>棒グラフ>累積コラムを選択します。
- ステッププロット-ギャラリー>線形>折れ線グラフを選択します。
- スパイクプロット-ギャラリー>線形>高/低を選択します。
- プロットする変数を選択します。
- ヒストグラム-変数 X としてヒストグラム X を選択し、変数 Y として階級化後の 1つ以上の列を選択します。
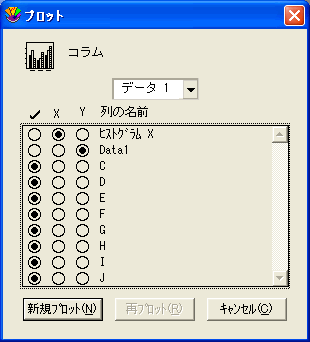
- ステッププロット-変数 X としてステップ X を選択し、変数 Y として階級化後の 1つ以上の列を選択します。
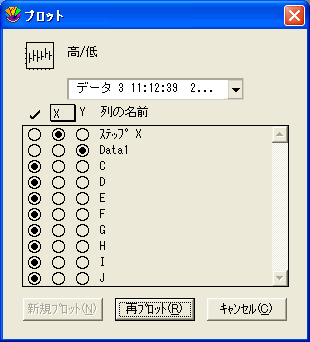
- スパイクプロット-変数 X としてスパイク X を選択し、変数 Y として階級化後の 1列とゼロを選択します。
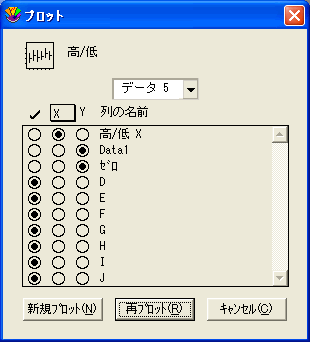
- 新規プロットをクリックします。
- ヒストグラム
- ステップ
- 高/低
統計的検定の選択
KaleidaGraph では、さまざまな検定を実行することができます。使用する検定の種類は、サンプル数とデータの特性によって異なります。
- 1標本の検定は、既知の値、または仮説値について1標本の解析に使用します。
- 群比較検定は、統計的に有意な差を示す 2つ以上のサンプルの解析に使用します。
- 反復測定の検定は、2つ以上の同数サンプル (同一数のサンプルについて 1回以上の処理の前と後など) の解析に使用します。
下表に、各実験と収集データの種類に対して適切な検定を示します。
パラメトリック検定とノンパラメトリック検定
KaleidaGraph の統計的検定は、パラメトリック検定とノンパラメトリック検定に分けることができます。
- パラメトリック検定
パラメトリック検定は、サンプルが等しい分散を持つ正規分布の母集団から抽出されたという前提に基づいています。パラメトリック検定の例として t-検定と分散分析があります。
- サンプルが正規分布の母集団から抽出されたことが確実に分かっている場合は通常、パラメトリック検定を使用します。
- ノンパラメトリック検定
ノンパラメトリック検定 (非正規分布検定) では、データの分散について前提がありません。この検定は、データを値の小さい順に順位付けし、その順位を解析します。ノンパラメトリック検定の例として、Wilcoxon、Kruskal-Wallis、Friedman の検定があります。
- データが順位やスコアを示す場合、また測定値が非正規分布の母集団から抽出されたものである場合は通常、ノンパラメトリック検定を使用します。
1標本の分析
概要: 1標本の分析
KaleidaGraph には、1標本の平均値または中央値と、仮説値に有意差があるかどうかを調べる 2種類の検定があります。これらの検定について説明します。
- 1群の t-検定は、サンプルが正規分布の母集団から抽出された場合に使用します。これは、1標本の平均値を既知の値、または仮説値と比較するパラメトリック検定です。
- Wilcoxon 符号順位検定は、非正規分布の母集団からサンプルが抽出された場合、またはデータが順位やスコアである場合に使用します。これは、1標本の中央値を既知の値、または仮説値と比較するノンパラメトリック検定です。
1群の検定のデータ入力
1群の t-検定と Wilcoxon 符号順位検定ではいずれも、サンプルのデータを 1列のデータ列に入力する必要があります。データにグループ化変数が含まれている場合は、グループ化変数も入力することができます。ただし、いずれの解析でもグループ化変数は使用されません。
■ 1群の t-検定
1群の t-検定の実行
サンプルの平均値を既知の値、または仮説値と比較するときにこの検定を使用します。
- 1群の t-検定を実行するには:
- 機能>t-検定を選択して、t-検定ダイアログを表示します。
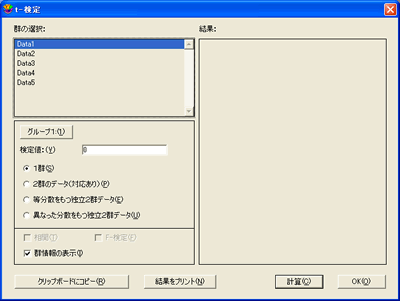
- 1群ボタンをクリックします。
- 列の名前 (Data1) をクリックしてグループ1 ボタンをクリックするか、列の名前 (Data1) をダブルクリックして、検定する列を選択します。
- 検定値フィールドに既知の値、または仮説値を入力します。
- 計算をクリックします。検定の結果がダイアログの右側に表示されます。
- 結果をエクスポートするには、クリップボードにコピーをクリックします。次に結果をデータ、プロット、またはレイアウトのウィンドウにペーストします。
- 結果を印刷するには、結果をプリントボタンをクリックします。
- OK をクリックして、データウィンドウに戻ります。
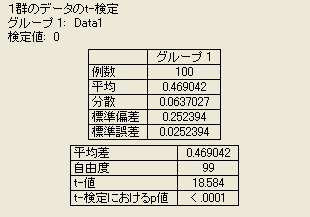
1群の t-検定の結果
- 1群の t-検定を実行すると、次の値が計算されます。
- 平均差-平均値と検定値の差を示します。
- 自由度-サンプルサイズの尺度です。
- t-値-Student の t検定値で、次の式で計算されます。
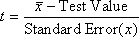
上の式の  はデータの平均値です。 はデータの平均値です。
- t-検定におけるp値-この値 (p値とも呼ばれる) は、サンプルの平均値と仮定の平均値との間に統計的に有意な差があるかどうかを示します。この値が一定レベル (通常は 0.05) 未満の場合、二者の間には差があると結論づけられます。
■ Wilcoxon 符号順位検定
Wilcoxon 符号順位検定の実行
この検定は 1群の中央値を既知の値、または仮説値と比較します。
この検定は、サンプルが正規分布の母集団から抽出されている必要のないノンパラメトリック検定です。サンプルが正規分布であることが分かっている場合は、1群の t-検定を使用します。
- Wilcoxon 符号順位検定を実行するには:
- 機能>Wilcoxon を選択して、Wilcoxon 検定ダイアログを表示します。
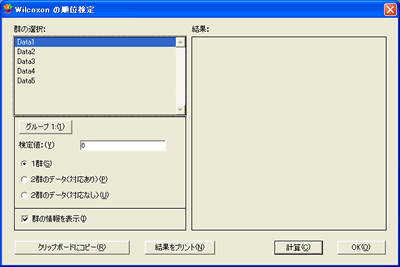
- 1群ボタンをクリックします。
- 列の名前をクリックしてグループ1をクリックするか、列の名前をダブルクリックして、検定する列を選択します。
- 検定値フィールドに既知の値、または仮説値を入力します。
- 計算をクリックします。検定の結果がダイアログの右側に表示されます。

- 結果をエクスポートするには、クリップボードにコピーをクリックします。次に結果をデータ、プロット、またはレイアウトのウィンドウにペーストします。
- 結果を印刷するには、結果をプリントボタンをクリックします。
- OK をクリックして、データウィンドウに戻ります。
Wilcoxon 符号順位検定の結果
- Wilcoxon 符号順位検定を実行すると、次の値が計算されます。
- 中央値の差-中央値と検定値の差を示します。
- 正数の順位合計 -検定値よりも大きい値を持つ順位の合計数を示します。
- 負数の順位合計 -検定値よりも小さい値を持つ順位の合計数を示します。
- p値-この値は、サンプルの中央値と仮定の中央値との間に統計的に有意な差があるかどうかを示します。この値が一定レベル (通常は 0.05) 未満の場合、二者の間には差があると結論づけられます。
- p値の算出法-KaleidaGraph での p値の計算方法を示します。
2群以上の解析
概要 : 2群以上の解析
KaleidaGraph には、2つ以上の標本について平均値または中央値の有意差を調べるための検定が 5種類あります。使用する検定は、標本数とデータの分散によって異なります。
- 2群の比較
データが異なる 2群のサンプル (例: オスとメスのマナティ) から収集された場合、次の群比較検定のいずれかを使用します。
- 3つ以上の群の比較
サンプルの母集団が等分散を持つ正規分布の場合は、次の群比較検定のいずれかを使用します。
- 一元配置分散分析は、3つ以上の群の平均値に対する単一因子の影響を比較します (例:動物試験体のグループに対する 3種類の薬品の影響)。
- 二元配置分散分析は、3つ以上の群の平均値に対する 2つの異なる因子の影響を比較します (例:動物試験体のグループについて、異なる時刻に与えた3種類の薬品の影響)。
- サンプルの母集団が非正規分布の場合、またはデータが順位やスコアの場合は、Kruskal-Wallis 検定を使用します。
| 注意: 一元配置分散分析で統計的に有意な差が検出された場合は、Post Hoc テストのいずれかを使用してどの群が異なるかを調べることができます。 |
群比較検定用データの入力
KaleidaGraph の群比較検定では、次のいずれかの方法でデータを入力する必要があります。
- 生データの場合は、各群のデータを個別の列に入力します (例を参照)。
- 2群の t検定 (対応なし) と Wilcoxon-Mann-Whitney 検定
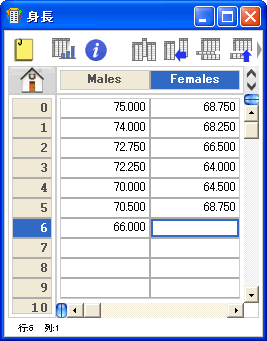
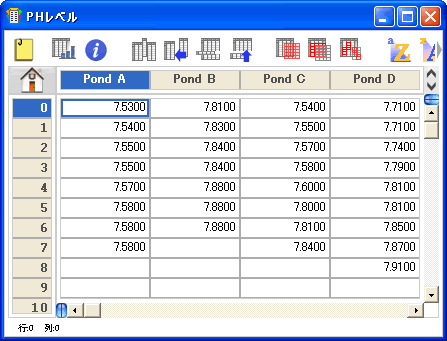
- 一元配置分散分析と Kruskal-Wallis 検定
- 群分けされたデータの場合は、入力する 1列は因子列またはグループ化変数で、対応するデータ点を 1つ以上の列に入力します (例を参照)。
- 独立2群t検定と Wilcoxon-Mann-Whitney 検定
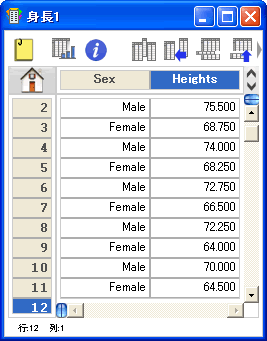
- 一元配置分散分析と Kruskal-Wallis 検定
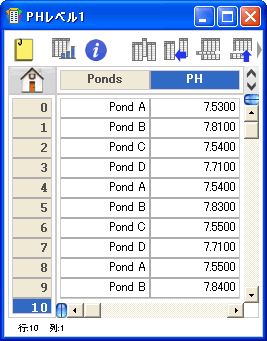
- 二元配置分散分析 (因子列1列とデータ列4列)
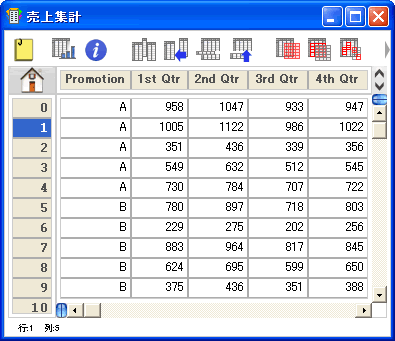
- 二元配置分散分析 (因子列 2列とデータ列 1列)
二元配置分散分析を除くすべての検定で生データを使用することができます。二元配置分散分析では、因子列が 1 または 2列、データ列が 1列以上ある必要があります。
| 注意: 二元配置分散分析を使用していない限り、群のサイズは同じでなくてもかまいません。二元配置分散分析では、均衡の取れたデータを使用しているものと仮定されます。マスクされているセルまたは空のセルが含まれている行はすべて無視されます。 |
■ 2群の t-検定 (対応なし)
2群の t-検定 (対応なし) の実行
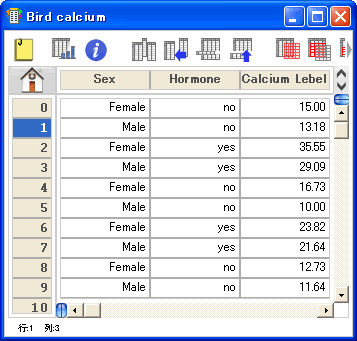
この検定は、2つの独立したサンプルの平均値を比較します。サンプル間の相関は仮定されていないので、この検定は長さの異なる列について実行することができます。特殊な場合として、グループ1 をテキスト列に割り当てた場合、グループ1 は第2列のデータを 2つのグループに分けるためのグループ化変数 (例:性別) として使用されます。
- 2群の t-検定 (対応なし) を実行するには:
- 機能>t-検定を選択して、t-検定ダイアログを表示します。
- 等分散をもつ独立2群データまたは異なった分散を持つ独立2群データのボタンをクリックします。
- 列の名前をクリックしてグループボタンをクリックするか、列の名前をダブルクリックして、検定する列を選択します。テキスト列をグループ化変数として使用する場合は、テキスト列をグループ列に割り当てる必要があります。
- F値および F検定における確率を計算する場合は、F-検定チェックボックスをオンにします。
- 計算をクリックします。検定の結果がダイアログの右側に表示されます。
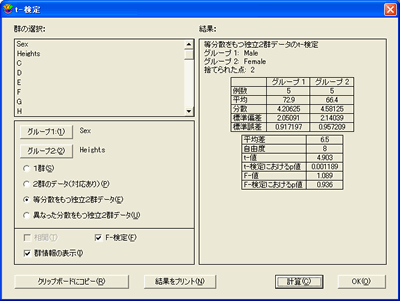
- 結果をエクスポートするには、クリップボードにコピーをクリックします。次に結果をデータ、プロット、またはレイアウトのウィンドウにペーストします。
- 結果を印刷するには、結果をプリントボタンをクリックします。
- OK をクリックして、データウィンドウに戻ります。
2群の t-検定 (対応なし) の結果
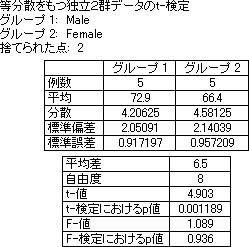
- 2群の検定 (対応なし) を実行すると、次の値が計算されます。
- 平均差-2つの平均値の差を示します。
- 自由度-サンプルサイズの尺度です。
- t-値-Student の t-検定値で、次の式で計算されます。
- 等分散をもつ独立2群データ
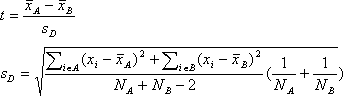
- 異なった分散をもつ独立2群データ
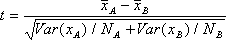
- t-検定におけるp値-この値 (p値とも呼ばれる) は、2つの平均値との間に統計的に有意な差があるかどうかを示します。この値が一定レベル (通常は 0.05) 未満の場合、二者の間には差があると結論づけられます。
- F-値-この値は、小さい分散に対する大きい分散の比率です。
- F-検定におけるp値-この値は、2つのグループの分散が異なるかどうかを示します。この値が小さい (通常 0.05 未満) 場合、2つのグループの分散には有意な差があることを示します。
- 上記の式で使用されている記号
- N : データ数
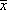 : データの平均値 : データの平均値- xi、yi : 現在のデータ値(1~N)
|
関連:データ分析例「対応のない t-検定の実行」
■ Wilcoxon-Mann-Whitney 検定
Wilcoxon-Mann-Whitney 検定の実行
この検定は、2つの異なるサンプルの母集団が同一であるかどうかを調べます。サンプル間の相関は仮定されていないので、この検定は長さの異なる列について実行することができます。特殊な場合として、グループ1 をテキスト列に割り当てた場合、グループ1 は第2列のデータを 2つのグループに分けるためのグループ化変数 (例:性別) として使用されます。
この検定は、サンプルが等分散をもつ正規分布ではないと仮定しています。サンプルが正規分布であることが分かっている場合は、2群の t-検定 (対応なし)を使用します。3つ以上のサンプルを比較する場合は、Kruskal-Wallis 検定を使用します。
- Wilcoxon-Mann-Whitney 検定を実行するには:
- 機能>Wilcoxon を選択して、Wilcoxon 検定ダイアログを表示します。
- 2群のデータ(対応なし)ボタンをクリックします。
- 列の名前をクリックしてグループボタンをクリックするか、列の名前をダブルクリックして、検定する列を選択します。テキスト列をグループ化変数として使用する場合は、テキスト列をグループ1に割り当てる必要があります。
- 計算をクリックします。検定の結果がダイアログの右側に表示されます。
- 結果をエクスポートするには、クリップボードにコピーをクリックします。次に結果をデータ、プロット、またはレイアウトのウィンドウにペーストします。
- 結果を印刷するには、結果をプリントボタンをクリックします。
- OK をクリックして、データウィンドウに戻ります。
Wilcoxon-Mann-Whitney 検定の結果
- Wilcoxon-Mann-Whitney 検定を実行すると、次の値が計算されます。
- 中央値の差-2つのグループの中央値の差を示します。
- グループ1の順位合計 -グループ1 の値の順位の合計値です。
- グループ2の順位合計 -グループ2 の値の順位の合計値です。
- グループ1のU値-グループ1 の Wilcoxon-Mann-Whitney の統計量 (U) で、次の式で計算されます。
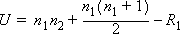
- グループ2のU値-グループ2 の Wilcoxon-Mann-Whitney の統計量 (U) で、次の式で計算されます。
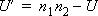
- p値-この値は、2つのグループの中央値に統計的に有意な差があるかどうかを示します。この値が一定レベル (通常は 0.05) 未満の場合、二者の間には差があると結論づけられます。
- p値の算出法-KaleidaGraph での p値の計算方法を示します。
- 上記の式で使用されている記号
- n1、n2 :グループ1、2のデータ数
- R1 :グループ1の順位の合計
|
■ 一元配置分散分析
一元配置分散分析の実行
この検定は、3つ以上の異なるグループが単一の因子の影響を受けているかどうかを調べる場合に使用します。この検定は 2群の t-検定 (対応なし) と同じですが、3つ以上のグループを比較できる点が異なります。

この検定は、サンプルの母集団が等分散をもつ正規分布であるという前提のパラメトリック検定です。サンプルが正規分布でないことが分かっている場合は、Kruskal-Wallis検定を使用します。比較するサンプル数が2つの場合は、2群のt-検定(対応なし)を使用します。
- 一元配置分散分析を実行するには:
- 機能>分散分析を選択して、分散分析ダイアログを表示します。
- 測定値をもつデータ列を従属変数リストに割り当てます。
- 群分けされたデータを使用する場合は、因子列を因子リストに割り当てます。この場合は、従属変数の列を1列だけ使用する必要があります。複数の列を従属変数リストに割り当てた場合、二元配置分散分析が実行されます。
- 計算をクリックします。検定の結果がダイアログの下半分に表示されます。
- 統計的に有意な差があると分かった場合は、Post Hocテストのいずれかを実行して、異なるグループと違いの差を調べることができます。
- 結果をエクスポートするには、クリップボードにコピーをクリックします。次に結果をデータ、プロット、またはレイアウトのウィンドウにペーストします。
- 結果を印刷するには、結果をプリントボタンをクリックします。
- OK をクリックして、データウィンドウに戻ります。
一元配置分散分析の結果
- 一元配置分散分析を実行すると、次の値が計算されます。自由度、平方和、および平均平方の値の計算式については、リファレンスを参照してください。
- 自由度-分散分析表のこの列には次の 3種類の自由度の値が表示されます。各自由度は次の式で計算されます。
- 自由度合計 =標本数-1
- グループの自由度 =グループ数-1
- 誤差の自由度 =標本数合計 -グループ数
- 平方和-分散分析表のこの列には、次の 3種類の平方和が表示されます。
- 平方和合計は、総平均(すべてのサンプルの平均値)に対するサンプル全体の変動を示します。
- グループの平方和は、グループ平均の間の変動を示します。
- 誤差の平方和は、各標本の変動を示します。
- 平均平方-分散分析表のこの列には、次の 3種類の平均平方が表示されます。
- 平均平方の合計は、自由度合計に対する平方和合計の比率です。
- グループの平均平方は、グループの自由度に対するグループの平方和の比率です。
- 誤差の平均平方は、誤差の自由度に対する誤差の平方和の比率です。
- F値-この値は、誤差の平均平方に対するグループの平均平方の比率です。この値が 1.0 の近似値である場合、グループ間に有意差はないと見なすことができます。この値が大きい場合、1つ以上の標本が異なる母集団から抽出されたと見なすことができます。異なるグループを特定するには、 Post Hocテストのいずれかを使用します。
- p値-この値は、2つのグループ間に統計的に有意な差があるかどうかを示します。この値が一定レベル (通常は 0.05) 未満の場合、2つのグループには差があると見なすことができます。
関連:データ分析例「一元配置分散分析の実行」
■ 二元配置分散分析
二元配置分散分析の実行
この検定は、3つ以上のグループが 2つの因子の影響を受けているかどうかを調べる場合に使用します。二元配置分散分析は、次の 3つの仮定を検定します。
- 第1因子のレベル間に差がない。
- 第2因子のレベル間に差がない。
- 因子間の交互作用がない。
この検定は、サンプルの母集団が等分散をもつ正規分布であるという前提のパラメトリック検定です。データに対する 1つの因子だけの影響を調べるには一元配置分散分析を使用します。KaleidaGraph には、二元配置分散分析に相当するノンパラメトリック検定はありません。
- 二元配置分散分析 (因子列1列とデータ列4列)

-
二元配置分散分析 (因子列 2列とデータ列 1列)

| 注意: 二配置分散分析では、マスクされているセルまたは空のセルが含まれている行はすべて無視されます。因子のそれぞれの観測値数が同じでなければなりません。 |
- 二元配置分散分析を実行するには:
- 機能>分散分析を選択して、分散分析ダイアログを表示します。
- 測定値をもつデータ列を従属変数リストに割り当てます。
- 1つ以上の因子列を因子リストに割り当てます。因子列を2列割り当てた場合は、従属変数列は1列だけ使用することができます。
- 計算をクリックします。検定の結果がダイアログの下半分に表示されます。
- 結果をエクスポートするには、クリップボードにコピーをクリックします。次に結果をデータ、プロット、またはレイアウトのウィンドウにペーストします。
- 結果を印刷するには、結果をプリントボタンをクリックします。
- OKをクリックして、データウィンドウに戻ります。
二元配置分散分析の結果
- 二元配置分散分析を実行すると、次の値が計算されます。自由度、平方合計、および平均平方の値の計算式については、リファレンスを参照してください。
- 自由度-分散分析表のこの列には次の5種類の自由度の値が表示されます。各自由度は次の式で計算されます。
- 自由度合計 =標本数-1
- 各因子の自由度 =因子のレベル数-1
- 交互作用の自由度 =因子A の自由度 x 因子B の自由度
- 残差の自由度 =自由度合計 -各因子の自由度 -交互作用の自由度
- 平方和-分散分析表のこの列には、次の 5種類の平方和が表示されます。
- 平方和合計は、データ変動性の合計です。
- 各因子の平方和は、各因子のレベル間の変動性を示します。
- 交互作用の平方和は、因子間の交互作用の指標を示します。
- 残差の平方和は、データのランダムな変化を示します。
- 平均平方-分散分析表のこの列には、次の 5種類の平均平方が表示されます。
- 平均平方の合計は、自由度合計に対する平方和合計の比率です。
- 各因子の平均平方は、因子の自由度に対する因子の平方合計の比率です。
- 交互作用の平均平方は、交互作用の自由度に対する交互作用の平方和の比率です。
- 残差の平均平方は、残差の自由度に対する残差の平方和の比率です。
- F値-因子と交互作用のそれぞれについて F値が計算されます。各因子について、この値は誤差の平均平方に対する因子の平均平方の比率です。交互作用については、この値は誤差の平均平方に対する交互作用の平均平方の比率です。
- この値が 1.0 に近い値である場合、因子レベルに有意差はない、または因子間の交互作用はないと見なすことができます。この値が大きい場合、因子または因子の組み合わせについて、1つ以上のサンプルが異なる母集団から抽出されたと見なすことができます。
- p値-この値は、グループ間に統計的に有意な差があるかどうかを示します。この値が一定レベル (通常は 0.05) 未満の場合、2つのグループには差があると見なすことができます。
関連:データ分析例「二元配置反復測定分散分析」
■ Kruskal-Wallis 検定
Kruskal-Wallis 検定の実行
この検定は、3群以上が単一因子の影響を受けているかどうかを調べる場合に使用します。

この検定は、標本の母集団が正規分布である必要がないノンパラメトリック検定です。標本が正規分布であることが分かっている場合は、一元配置分散分析を使用します。比較するサンプル数が 2つの場合は、Wilcoxon-Mann-Whitney 検定を使用します。
- Kruskal-Wallis 検定を実行するには:
- 機能>Kruskal-Wallisを選択して、Kruskal-Wallis ダイアログを表示します。
- 測定値をもつデータ列を従属変数リストに割り当てます。
- 群分けされたデータを使用する場合は、因子列を因子リストに割り当てます。この場合は、従属変数の列が1列だけ使用できます。
- 計算をクリックします。検定の結果がダイアログの下半分に表示されます。
- 結果をエクスポートするには、クリップボードにコピーをクリックします。次に結果をデータ、プロット、またはレイアウトのウィンドウにペーストします。
- 結果を印刷するには、結果をプリントボタンをクリックします。
- OK をクリックして、データウィンドウに戻ります。
Kruskal-Wallis 検定の結果
- Kruskal-Wallis 検定を実行すると、次の値が計算されます。
- Kruskal-Wallisの統計量-これは Kruskal-Wallis の検定値 (H) で、次の式で計算されます。
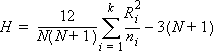
- p値-Kruskal-Wallis の統計量に対応する p値で、グループの中央値の間に有意な差があるかどうかを示します。この値が一定レベル (通常は 0.05) 未満の場合、グループ間に差があると見なすことができます。
- 算出法-KaleidaGraph での p値の計算方法を示します。
- 上記の式で使用されている記号
- k : グループ数
- ni : グループ i のデータ数
- N : k 個のグループ全体のデータ数
- Ri : グループ i のデータ数 ni の順位合計
|
反復測定の分析
概要: 反復測定の分析
KaleidaGraph には、2つ以上の同数サンプルについて平均値や中央値に有意な差があるかどうかを分析するための検定が 5種類用意されています。使用する検定方法は、サンプル数とデータの分布によって異なります。
- 2群の比較
データが同一グループから収集された場合 (例:多数の自動車についてチューンアップ前後の燃費) は、次の反復測定検定のいずれかを使用します。
- 2群の比較t-検定 (対応あり)は、サンプルの母集団が等分散をもつ正規分布である場合に使用します。これはサンプルデータを直接比較するパラメトリック検定です。
- Wilcoxon 符号順位和検定は、サンプルの母集団が正規分布でない場合、またはデータが順位やスコアの場合に使用します。これは、データに順位付けするノンパラメトリック検定で、生データではなく順位を分析します。
- 3群以上の比較
3群以上の同等のグループから収集したデータを比較するには、反復測定による一元配置分散分析、反復測定による二元配置分散分析、または Friedman 検定を使用します。
サンプルの母集団が等分散をもつ正規分布である場合は、反復測定による一元配置分散分析、または反復測定による二元配置分散分析を使用します。
- 反復測定による一元配置分散分析は、同等な 3群以上の平均に対する単一因子の影響を比較します (例:処置の前、途中、および後における被験体に対する薬品の影響の比較)。
- 反復測定による二元配置分散分析は、同等な 3群以上の平均に対する 2つの異なる因子の影響を比較します (例:処置の前、途中、および後におけるオスとメスに対する薬品の影響の比較)。
- サンプルの母集団が正規分布でない場合、またデータが順位やスコアである場合は、Friedman 検定を使用します。
| 注意: 反復測定による一元配置分散分析により統計的に有意な差があると分かった場合は、Post Hoc テストのいずれかを使用して異なるグループを調べることができます。 |
反復測定のデータ入力
KaleidaGraph の反復測定の検定では、データを生データとして入力する必要があり、各処理は個別の列に入力する必要があります (例を参照)。
唯一の例外は反復による二元配置分散分析で、索引付きデータを入力する必要があります。この場合、列のうち1列は因子列またはグループ化変数で、対応するデータ点を2列以上の列に入力します (例を参照)。
- データの例-反復測定
- 2群の t-検定 (対応あり) と Wilcoxon 符号順位和(マッチドペア)検定
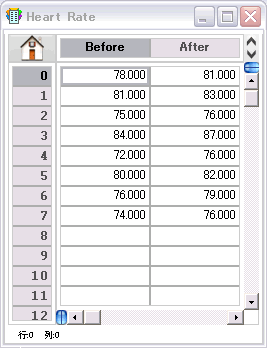
- 反復測定一元配置分散分析と Friedman 検定
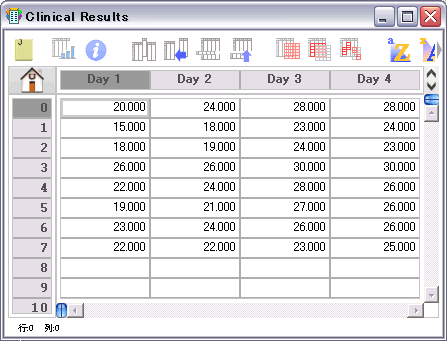
- 反復測定二元配置分散分析
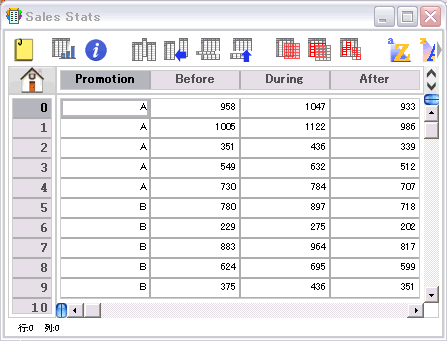
| 注意: 分析対象の各グループのデータ数は等しい必要があります。 |
■ 2群の比較 t-検定 (対応あり)
2群の比較 t-検定 (対応あり) の実行
この検定は、時系列的、または異なる条件での同一事象、または関連事象の平均値を比較します。この検定では各グループの列の長さが同一である必要があり、余分なデータがある、またはデータが不足しているデータ点は、検定の実行時に対象外となります。

- 2群の比較t-検定 (対応あり) を実行するには:
- 機能>t-検定を選択してt-検定ダイアログを表示します。
- 2群のデータ(対応あり) ボタンをクリックします。
- 列の名前をクリックしてグループボタンをクリックするか、列の名前をダブルクリックして、検定する列を選択します。
- 相関値と相関の確率を計算する場合は、相関チェックボックスをオンにします。
- 計算をクリックします。検定の結果がダイアログの右側に表示されます。
- 結果をエクスポートするには、クリップボードにコピーをクリックします。次に結果をデータ、プロット、またはレイアウトのウィンドウにペーストします。
- 結果を印刷するには、結果をプリントボタンをクリックします。
- OK をクリックして、データウィンドウに戻ります。
2群の比較 t-検定 (対応あり) の結果
- 関連 2群 t-検定を実行すると、次の値が計算されます。
- 平均値の差-2つの平均値の差です。
- 自由度-サンプルサイズの尺度です。
- t値-Student の t検定値で、次の式で計算されます。
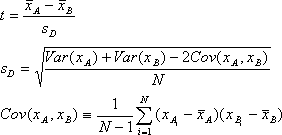
- t確率-この値 (p値とも呼ばれる) は、2つのグループの平均値の間に統計的に有意な差があるかどうかを示します。この値が一定レベル (通常は 0.05) 未満の場合、2つのグループの間には差があると見なすことができます。
- 相関-この値は、2つのグループの線形相関係数を表します。この値が 1.0 に近いほど、2つのグループの相関が高くなります。相関は次の式で計算されます。
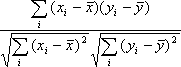
- 相関におけるp値-この値は、2つのグループの相関の有無を示します。この値が小さい (通常 0.05 未満)場合、2つのグループには有意な相関があることを示します。
- 上記の式で使用されている記号
- N : データ数
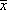 : データの平均値 : データの平均値- xi、yi : 現在のデータ値(1~N)
|
関連:データ分析例「対応のある t-検定の実行」
■ Wilcoxon マッチドペア検定
Wilcoxon マッチドペア検定の実行
この検定は、時系列的、または異なる条件での同一事象、または関連事象の中央値を比較します。この検定では各グループの列の長さが同一である必要があり、データが欠落している、または余分なデータ点は、検定の実行時に対象外となります。

この検定は、サンプルが等分散の正規分布ではないと仮定しています。サンプルが正規分布であることが分かっている場合は、2群の比較 t-検定 (対応あり)を使用します。比較するグループが 3つ以上の場合は、Friedman 検定を使用します。
- Wilcoxon マッチドペア検定を実行するには:
- 機能>Wilcoxon を選択して、Wilcoxon検定 ダイアログを表示します。
- 2群のデータ(対応あり)ボタンをクリックします。
- 列の名前をクリックしてグループボタンをクリックするか、列の名前をダブルクリックして、検定する列を選択します。
- 計算をクリックします。検定の結果がダイアログの右側に表示されます。
- 結果をエクスポートするには、クリップボードにコピーをクリックします。次に結果をデータ、プロット、またはレイアウトのウィンドウにペーストします。
- 結果を印刷するには、結果をプリントボタンをクリックします。
- OK をクリックして、データウィンドウに戻ります。
Wilcoxon マッチドペア検定の結果
- Wilcoxon マッチドペア検定を実行すると、次の値が計算されます。
- 中央値の差-2つのグループの中央値の差を示します。
- 正数の順位合計 -この値は、2つのグループの差を計算したときにグループ 1 のほうが大きい順位 (正数の順位)の合計を示します。
- 負数の順位合計-この値は、2つのグループの差を計算したときにグループ 2 のほうが大きい順位 (負数の順位)の合計を示します。
- p値 -この値は、2つのグループの中央値に統計的な有意差があるかどうかを示します。この値が一定レベル (通常は 0.05) 未満の場合、グループ間に差があると見なすことができます。
- p値の算出法-KaleidaGraph での p値の計算方法を示します。
■ 反復測定一元配置分散分析
反復測定一元配置分散分析の実行
この検定は、同一グループ内の個々が単一因子の影響を受けているかどうかを調べる場合に使用します。この検定は 2群の比較 t-検定 (対応あり) と同じですが、3つ以上の処理を比較できる点が異なります。

これは、サンプルの母集団が等分散の正規分布であると仮定したパラメトリック検定です。サンプルが正規分布でないことが分かっている場合は、Friedman検定を使用します。比較するグループが 2つの場合は、2群の比較t-検定(対応あり)を使用します。
| 注意: この検定では、列の長さが同じである必要があります。値が欠落している、または余分な値をもつデータ点がある場合は、一元配置分散分析が実行されます。 |
- 反復測定による一元配置分散分析を実行するには:
- 機能>分散分析を選択して、分散分析ダイアログを表示します。
- 測定値をもつデータ列を従属変数リストに割り当てます。
- 反復測定チェックボックスをオンにします。
- 反復因子名フィールドにラベル名を入力します。このラベルは分散分析表に表示されます。
- 計算をクリックします。検定の結果がダイアログの下半分に表示されます。
- 統計的に有意な差があると分かった場合は、Post Hoc テストのいずれかを使用して異なるグループと違いの程度を調べることができます。
- 結果をエクスポートするには、クリップボードにコピーをクリックします。次に結果をデータ、プロット、またはレイアウトのウィンドウにペーストします。
- 結果を印刷するには、結果をプリントボタンをクリックします。
- OK をクリックして、データウィンドウに戻ります。
反復測定一元配置分散分析の結果
- 反復測定一元配置分散分析を実行すると、次の値が計算されます。自由度、平方和、および平均平方の値の計算式については、リファレンスを参照してください。
- 自由度-分散分析表のこの列には次の4種類の自由度の値が表示されます。各自由度は次の式で計算されます。
- 自由度合計 =標本総数-1
- 処理の自由度 = 処理数(列数) - 1
- 対象の自由度 =対象の数(行数) -1
- 残差の自由度 =自由度合計 -処理の自由度 -対象の自由度
- 平方和-分散分析表のこの列には、次の 4種類の平方和が表示されます。
- 平方和の合計は、データ変動性の合計です。
- 処理の平方和は、処理に対する対象の反応の平均の変動性を示します。
- 対象の平方和は、各対象の平均的応答の変動性を示します。
- 誤差の平方和は、対象間の差を考慮した上でのデータの変動性を示します。
- 平均平方-分散分析表のこの列には、次の 4種類の平均平方が表示されます。
- 平均平方の合計は、自由度の合計に対する平方和の合計の比率です。
- 処理の平均平方は、処理の自由度に対する処理の平方和の比率です。
- 対象の平均平方は、対象の自由度に対する対象の平方和の比率です。
- 誤差の平均平方は、誤差の自由度に対する誤差の平方和の比率です。
- F値-処理と対象のそれぞれについて F値が計算されます。処理については、この値は誤差の平均平方に対する処理の平均平方の比率です。対象については、個の値は誤差の平均平方に対する対象の平均平方の比率です。
- この値が 1.0 に近い値である場合、処理間にに有意差はないと見なすことができます。この値が大きい場合、処理による影響が異なると見なすことができます。異なる処理を調べるには、Post Hoc テストのいずれかを使用します。
- p値-この値は、処理間に統計的に有意な差があるかどうかを示します。この値が一定レベル (通常は 0.05) 未満の場合、処理間に差があると見なすことができます。
■ 反復測定二元配置分散分析
反復測定二元配置分散分析の実行
この検定は、同一グループの個々の対象が2つの因子の影響を受けるかどうかを調べる場合に使用します。少なくとも 1つの因子が同一グループの個々の対象についての反復処理です。反復測定二元配置分散分析は、次の 3つの仮定を検定します。
- 第1因子のレベルまたは処理に差がない。
- 第2因子のレベルまたは処理に差がない。
- 因子間の交互作用がない。

これは、サンプルの母集団が等分散の正規分布であると仮定したパラメトリック検定です。グループに対する1つの因子の影響を調べる場合は、反復測定一元配置分散分析を使用します。KaleidaGraph には、反復測定二元配置分散分析に相当するノンパラメトリック検定はありません。
| 注意: この検定では、各グループのデータ数が等しい必要があります。 |
- 反復測定二元配置分散分析を実行するには:
- 機能>分散分析を選択して、分散分析ダイアログを表示します。
- 測定値をもつデータ列を従属変数リストに割り当てます。
- 因子列を因子リストに割り当てます。
- 反復測定チェックボックスをオンにします。
- 反復因子名フィールドにラベル名を入力します。このラベルは分散分析表に表示されます。
- 計算をクリックします。検定の結果がダイアログの下半分に表示されます。
- 結果をエクスポートするには、クリップボードにコピーをクリックします。次に結果をデータ、プロット、またはレイアウトのウィンドウにペーストします
- 結果を印刷するには、結果をプリントボタンをクリックします。
- OK をクリックして、データウィンドウに戻ります。
反復測定二元配置分散分析の結果
- 反復測定二元配置分散分析を実行すると、次の値が計算されます。自由度、平方和、および平均平方の値の計算式については、リファレンスを参照してください。
- 自由度-分散分析表のこの列には次の6種類の自由度の値が表示されます。各自由度は次の式で計算されます。
- 自由度合計 =標本総数-1
- 各因子の自由度 =因子のレベル数-1
- 交互作用の自由度 =因子Aの自由度 x 因子Bの自由度
- 対象の自由度は対象数(行数)の尺度です。
- 誤差の自由度 =自由度合計 -因子の自由度 -交互作用の自由度 -対象の自由度
- 平方和-分散分析表のこの列には、次の 6種類の平方和が表示されます。
- 平方和の合計は、データの変動性の合計です。
- 各因子の平方和は、各因子の処理の変動性を示します。
- 交互作用の平方和は、両方の因子に対する処理の変動性を示します。
- 対象の平方和は、すべての対象の変動性を示します。
- 誤差の平方和は、データに含まれる変動を示します。
- 平均平方-分散分析表のこの列には、次の 6種類の平均平方が表示されます。
- 平均平方合計は、自由度の合計に対する平方和の合計の比率です。
- 各因子の平均平方は、因子の自由度に対する因子の平方和の比率です。
- 交互作用の平均平方は、交互作用の自由度に対する交互作用の平方和の比率です。
- 対象の平均平方は、対象の自由度に対する対象の平方和の比率です。
- 誤差の平均平方は、誤差の自由度に対する誤差の平方和の比率です。
- F値-因子、交互作用、および対象についてそれぞれF値が計算されます。この値が 1.0 に近い値である場合、処理間に有意差はないと見なすことができます。この値が大きい場合、処理が与える影響に差があると見なすことができます。
- 第1因子については、この値は対象の平均平方に対する因子の平均平方の比率です。
- 第2因子については、この値は誤差の平均平方に対する因子の平均平方の比率です。
- 交互作用については、この値は誤差の平均平方に対する交互作用の平均平方の比率です。
- 対象については、個の値は誤差の平均平方に対する対象の平均平方の比率です。
- p値-この値は、処理間に統計的に有意な差があるかどうかを示します。この値が一定レベル (通常は 0.05) 未満の場合、処理間に差があると見なすことができます。
■ Friedman 検定
Friedman 検定の実行
この検定は、単一グループ内の個々の対象が 3つ以上の一連の処理の影響を受けているかどうかを調べる場合に使用します。

この検定は、サンプルの母集団が正規分布である必要がないノンパラメトリック検定です。サンプルが正規分布であることが分かっている場合は、一元配置分散分析を使用します。比較するサンプル数が 2つの場合は、Wilcoxonマッチドペア検定を使用します。
| 注意: この検定では、列の長さが等しい必要があります。 |
- Friedman 検定を実行するには:
- 機能>Friedman を選択して、Friedman 検定ダイアログを表示します。
- 測定値をもつデータ列を従属変数リストに割り当てます。
- 計算をクリックします。検定の結果がダイアログの下半分に表示されます。
- 結果をエクスポートするには、クリップボードにコピーをクリックします。次に結果をデータ、プロット、またはレイアウトのウィンドウにペーストします。
- 結果を印刷するには、結果をプリントボタンをクリックします。
- OK をクリックして、データウィンドウに戻ります。
Friedman 検定の結果
- Friedman 検定を実行すると、次の値が計算されます。
- Friedman の統計量-この値は Friedman のカイ2乗統計量(χ2r)を示し、次の式で計算されます。
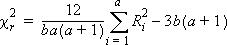
- p値-Friedman のカイ2乗統計量に対応するp値です。この値が一定レベル (通常は 0.05) 未満の場合、グループ間に差があると見なすことができます。
- 算出法-KaleidaGraph での p値の計算方法を示します。
- FF 統計量-Friedman の検定値 (FF) で、 Friedman のカイ2乗統計量を示す別の形式です。次の式で計算されます。
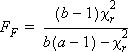
- FF p値-Friedman の検定値に対応するp値で、グループ間に有意差があるかどうかを示します。この値が一定レベル (通常は 0.05) 未満の場合、グループ間に差があると見なすことができます。
- 自由度-自由度を示します。
- 一致係数-Kendall の一致係数 (W) を示し、値の範囲は 0 (グループ間に関連がない) ~ 1 (グループの順位に一定の規則がある) です。この値は次の式で計算されます。
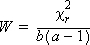
- 上記の式で使用されている記号
- a :グループ数
- b :行数(ブロック数)
- Ri :各グループ内の順位の合計
- χ2r :Friedmanの検定値
|
Post Hoc テストの実行
Post Hoc テストの選択
一元配置分散分析または一元配置反復測定分散分析を実行し、統計的に有意の差が見つかった場合は、次の post hoc 検定の 1つを使用して、どの群が異なっているのかを調べることができます。
ご存知のように、使用可能な post hoc 検定は多数存在します。ただし、どの検定が最も優れているかについては意見が分かれるところです。Tukey HSD および Student-Newman-Keuls 検定は、他の検定よりも幅広く受け入れられ、一般的に使用されています。Fisher の LSD 検定は最も保守的でないため、この検定を好む人もいます。どの検定を使用して良いか不明の場合は、いくつかの検定を使用して実験してみるとよいでしょう。
- Post Hoc テストを実行するには:
- 分散分析表の第1行に一元配置分散分析、または一元配置分散分析-反復測定が表示されていることを確認します。Post Hoc テストは二元配置分散分析や反復測定による二元配置分散分析では使用できません。
- Post Hoc テストのポップアップメニューから、使用するテストを選択します。
- 必要に応じて、有意水準ポップアップメニューから異なる有意レベルを選択します。
- 計算をクリックします。Post Hoc テストの結果が分散分析表の下に表示されます。
■ Tukey HSD 法
Tukey HSD (honestly significant difference) 法は、グループの組み合わせのすべてを比較します。各処理またはグループの組み合わせの平均値の差、および各組み合わせの q検定値を計算し、比較の p値を表示します。Tukey HSD 検定はすべての比較の誤差を同時に制御するため、Student-Newman-Keuls 検定よりも保守的です。
- Tukey HSD Post Hoc 法を実行するには:
- 分散分析表の第1行に一元配置分散分析、または一元配置分散分析-反復測定が表示されていることを確認します。Post Hoc テストは二元配置分散分析や反復測定による二元配置分散分析では使用できません。
- Post Hoc テストのポップアップメニューから Tukey HSD を選択します。
- 必要に応じて、有意水準ポップアップメニューから異なる有意レベルを選択します。
- 計算をクリックします。Post Hoc テストの結果が分散分析表の下に表示されます。
- Tukey HSD Post Hoc テストでは、次の値が計算されます。平均値の差、q、信頼限界の計算方法については、リファレンスを参照してください。
- 平均値の差-比較するグループや処理間の差を示します。
- |q|-この値は q検定値で、この値が大きい場合、比較する 2つの処理またはグループ間に統計的に有意な差があることを示します。
- p値-q 統計値に対応する p 値で、比較する処理やグループ間に統計的な有意差があるかどうかを示します。この値が一定レベル (通常は 0.05) 未満の場合、グループ間に差があると見なすことができます。
- 95%信頼限界-この値は、処理またはグループの平均値のすべての組み合わせに対する信頼限界を示します。選択した有意水準の値に合わせて、90 %、95 %、または 99 % 信頼限界として表示されます。
関連:Post Hoc 検定の実行
■ Student-Newman-Keuls 検定
Student-Newman-Keuls 検定は、群の対のすべての組み合わせの対比較です。この検定は、各処理または群の対の平均値の差を計算し、各対の q検定統計量を計算して、その比較の p値を表示します。
この検定では、q検定統計量の計算を除き、Tukey HSD 検定と同じように計算が行われます。この検定はTukey HSD 検定より保守的ではなく、所定の差が統計的に有意であると決定する傾向があります。
- Student-Newman-Keuls post hoc 検定を実行するには
- 一元配置分散分析の結果の最初の行に、一元配置分散分析または一元配置反復測定分散分析が存在することを確認します。二元配置分散分析または二元配置反復測定分散分析では、post hoc 検定は使用できません。
- Post Hoc テストポップアップメニューで Student-Newman-Keuls を選択します。
- 必要に応じて、有意水準ポップアップメニューで有意水準を変更します。
- 計算をクリックします。Post Hoc テストの結果が分散分析表の下に表示されます。
- Student-Newman-Keuls post hoc 検定を実行すると、下記の値が計算されます。平均値の差および q値の計算に使用されている方程式の詳細については、リファレンスを参照してください。
- 平均値の差-この値は、比較する群または処理の平均値間の差を表します。
- |q|-この値は、q検定統計量です。大きな q の値は、比較した 2つの処理または 2群の差が統計的に有意であることを示します。
- p値-この値は、q検定統計量に対応する p値を表します。この値は、比較した処理または群間に統計的に有意な差が存在するかどうかを決定します。この値がある水準 (通常は 0.05) 以下の場合は、群間に差が存在すると結論することができます。
■ Bonferroni 法
Bonferroni 法は、2グループのすべての組み合わせを比較します。処理またはグループの各組み合わせについての平均値の差、各組み合わせの t検定値を計算し、比較に対するp値を表示します。 この検定は、Tukey HSD 検定および Student-Newman-Keuls 検定より保守的です。
- Bonferroni Post Hoc テストを実行するには:
- 分散分析表の第1行に一元配置分散分析、または一元配置分散分析-反復測定が表示されていることを確認します。Post Hoc テストは二元配置分散分析や反復測定による二元配置分散分析では使用できません。
- Post Hoc テストのポップアップメニューから Bonferroni を選択します。
- 必要に応じて、有意水準ポップアップメニューから異なる有意レベルを選択します。
- 計算をクリックします。Post Hoc テストの結果が分散分析表の下に表示されます。
- Bonferroni Post Hoc テストでは、次の値が計算されます。平均値の差、t、信頼限界の計算方法については、リファレンスを参照してください。
- 平均値の差-比較するグループや処理間の平均値の差を示します。
- |t|-この値はt検定値で、この値が大きい場合、比較する 2つの処理またはグループ間に統計的に有意な差があることを示します。
- p値-t統計値に対応する p値で、比較する処理やグループ間に統計的な有意差があるかどうかを示します。この値が一定レベル (通常は 0.05) 未満の場合、グループ間に差があると見なすことができます。
- 95% 信頼限界-この値は、処理またはグループの平均値のすべての組み合わせに対する信頼限界を示します。選択した有意水準の値に合わせて、90 %、95 %、または 99 % 信頼限界として表示されます。
■ Holm 法
Holm 法は、2グループのすべての組み合わせを比較します。処理またはグループの各組み合わせについての平均値の差、各組み合わせのt検定値を計算し、比較に対する両側 p値を表示します。
p値の最小値が調整された有意水準の値と比較されます。p値が調整された有意水準の値以上である場合、このテストおよび残りの比較について有意差はないと見なすことができます。p値が調整された有意水準の値未満である場合は、このテストについて統計的な有意差があります。有意水準がさらに調整され、2番目に小さい p値についてテストが行われます。
この検定は、Bonferroni 検定を修正したものです。Holm 検定では、Bonferroni 検定では統計的に有意な差が見つからないときでも、差が見つかることがあります。この検定の欠点は、Bonferroni 検定の場合と同じように、信頼区間が示されないことです。
- Holm Post Hoc テストを実行するには:
- 分散分析表の第1行に一元配置分散分析、または一元配置分散分析-反復測定が表示されていることを確認します。Post Hoc テストは二元配置分散分析や反復測定による二元配置分散分析では使用できません。
- Post Hoc テストのポップアップメニューから Holm を選択します。
- 必要に応じて、有意水準ポップアップメニューから異なる有意レベルを選択します。
- 計算をクリックします。Post Hoc テストの結果が分散分析表の下に表示されます。
- Holm Post Hoc テストでは、次の値が計算されます。平均値の差、t、調整された有意水準の計算方法については、リファレンスを参照してください。
- 平均値の差-比較するグループや処理間の平均値の差を示します。
- |t|-t検定値です。
- 2-P-t検定値に対応する両側 p値です。
- 調整された有意水準-この値は、処理やグループ間に統計的な有意差があるかどうかを調べるために使用されます。この値は有意水準、両側 p値の順位、および実行するテスト数に基づいて計算されます。
- 有意差-両側 p値が調整された有意水準の値未満の場合は、比較する 2つの処理またはグループ間に統計的な有意差があります。
■ Scheffe 検定
Scheffe 検定は、群の対のすべての組み合わせの対比較です。この検定は、各処理または群の対の平均値の差を計算し、各対のS検定統計量を計算して、その比較の p値を表示します。
Scheffe の検定は他の post hoc 検定よりも保守的です。つまり、有意であるためには平均値間の差が大きくなければなりません。この検定は保守的であるために、Tukey HSD や Student-Newman-Keuls の検定ほど統計的には強力ではありません。
- Scheffe post hoc検定を実行するには
- 一元配置分散分析の結果の最初の行に、一元配置分散分析または一元配置反復想定分散分析が存在することを確認します。二元配置分散分析または二元配置反復測定分散分析では、post hoc 検定は使用できません。
- Post Hoc テストポップアップメニューで Scheffe を選択します。
- 必要に応じて、有意水準ポップアップメニューで有意水準を変更します。
- 計算をクリックします。Post Hoc テストの結果が分散分析表の下に表示されます。
- Scheffe post hoc 検定を実行すると、下記の値が計算されます。平均値の差、S値、および信頼限界の計算に使用されている方程式の詳細については、リファレンスを参照してください。
- 平均値の差-この値は、比較する群または処理の平均値間の差を表します。
- |S|-この値は S 検定統計量です。大きな S の値は、比較した 2つの処理または 2群の差が統計的に有意であることを示します。
- p値-この値は、S 検定統計量に対応する p値を表します。この値は、比較した処理または群間に統計的に有意な差が存在するかどうかを決定します。この値がある水準 (通常は 0.05) 以下の場合は、群間に差が存在すると結論することができます。
- 95% 信頼限界-この値は、処理または群の可能なすべての組み合わせ間の差の信頼限界を表します。選択した有意水準の値に合わせて、90%、95%、または 99% 信頼限界として表示されます。
■ Fisher の LSD 検定
Fisher の LSD (最小有意差) 検定は、群の対のすべての組み合わせの対比較です。この検定は、各処理または群の対の平均値の差を計算し、各対の t検定統計量を計算して、その比較の p値を表示します。
Fisher の LSD 検定は、すべての処理または群間の多重 t検定と等価です。この検定は、実行する検定の数に基づいて調整が行われないため、最も保守的でない post hoc 検定と言えます。
- FIsher の LSD post hoc 検定を実行するには
- 一元配置分散分析の結果の最初の行に、一元配置分散分析または一元配置反復測定分散分析が存在することを確認します。二元配置分散分析または二元配置反復測定分散分析では、post hoc 検定は使用できません。
- Post Hoc テストポップアップメニューで Fisher のLSD を選択します。
- 必要に応じて、有意水準ポップアップメニューで有意水準を変更します。
- 計算をクリックします。post hoc test 検定の結果が、分散分析表の下に表示されます。
- フィッシャーの LSD 検定 post hoc 検定を実行すると、下記の値が計算されます。平均値の差および t値の計算に使用されている方程式の詳細については、レファレンスを参照してください。
- 平均値の差-この値は、比較する群または処理の平均値間の差を表します。
- |t|-この値は t検定統計量です。大きなtの値は、比較した 2つの処理または 2群の差が統計的に有意であることを示します。
- p値-この値は、t検定統計量に対応する p値を表します。この値は、比較した処理または群間に統計的に有意な差が存在するかどうかを決定します。この値がある水準 (通常は 0.05) 以下の場合は、群間に差が存在すると結論することができます。
■ Dunnett 法
Dunnett 法は、基準群とした 1グループの平均値と、他のグループの個々の平均値との間に有意差があるかどうかを調べる場合に使用します。
- Dunnett Post Hoc テストを実行するには:
- 分散分析表の第1行に一元配置分散分析、または一元配置反復測定分散分析が表示されていることを確認します。Post Hoc テストは二元配置分散分析や二元配置反復測定分散分析では使用できません。
- Post Hoc テストのポップアップメニューから Dunnett を選択します。
- 必要に応じて、有意水準ポップアップメニューから異なる有意レベルを選択します。
- 計算をクリックします。Post Hoc テストの結果が分散分析表の下に表示されます。
- Dunnett Post Hoc テストでは、次の値が計算されます。平均値の差、q、信頼限界の計算方法については、リファレンスを参照してください。
- 平均値の差-比較するグループや処理間の差を示します。
- |q|-この値は q検定値で、この値が大きい場合、基準群と比較するグループ間に統計的な有意差があることを示します。
- p値-q検定値に対応する p値で、基準群と比較するグループとの間に統計的な有意差があるかどうかを示します。この値が一定レベル (通常は 0.05) 未満の場合、差があると見なすことができます。
- 95%信頼限界-この値は、基準群の平均値と他のグループの各平均値の差に対する信頼限界を示します。選択した有意水準の値に合わせて、90 %、95 %、または 99 % 信頼限界として表示されます。
参考資料
回帰曲線の参考資料
- 一般および 3次元スプライン回帰曲線
Press, W.H., Flannery, B.P., Teukolsky, S.A., and Vetterling, W.T. Numerical Recipes in C. Cambridge University Press, New York (1988).
- 線形、多項式、指数、対数、累乗回帰曲線
Beyer, W.H. Standard Mathematical Tables. CRC Press, Cleveland (1976).
- スムースおよび補間回帰曲線
Stineman, R.W. A consistently well-behaved method of interpolation. Creative Computing, July (1980).
- 加重回帰曲線
Chambers, J.M., Cleveland, W.S., Kleiner, B., and Tukey, P.A. Graphical Methods for Data Analysis. Duxbury Press, Boston (1983).
統計の参考資料
- Wilcoxon の符号順位検定、Wilcoxon-Mann-Whitney 検定、Kruskal-Wallis 検定、およびFriedman 検定
Siegel, S. and Castellan, N.J.Jr. Nonparametric Statistics for the Behavioral Sciences. McGraw-Hill, New York (1988).
Zar, J.H. Biostatistical Analysis. Prentice-Hall, Upper Saddle River, NJ (1999).
- 一元配置分散分析、二元配置分散分析、Tukey HSD、Student-Newman-Keuls、および Scheffe 検定
Zar, J.H. Biostatistical Analysis. Prentice-Hall, Upper Saddle River, NJ (1999).
Neter, J., Kutner, M.H., Nachtsheim, C.J., and Wasserman, W. Applied Linear Statistical Models. McGraw-Hill, New York (1996).
- Wilcoxon の Matched Pairs と Dunnett テスト
Zar, J.H. Biostatistical Analysis. Prentice-Hall, Upper Saddle River, NJ (1999).
- One Way Repeated Measures ANOVA, Two Way Repeated Measures ANOVA, Bonferroni テスト、および Holm テスト
Neter, J., Kutner, M.H., Nachtsheim, C.J., and Wasserman, W. Applied Linear Statistical Models. McGraw-Hill, New York (1996).
- Fisher の LSD 検定
Wilcox, Rand R. Applying Contemporary Statistical Techniques. Academic Press, San Diego, CA (2003).
|

