 |
| サイトマップ | |
|
 |
| サイトマップ | |
|
Regression Wizard は、カーブフィッティングを行う度に自動的にレポートを作成します。統計結果は、デフォルトで少数点第4位の精度で表示されます。
レポートは、SigmaPlot のレポートエディタを使って表示されます。
これは回帰結果の生成に使用するコードの内容を出力したものです。
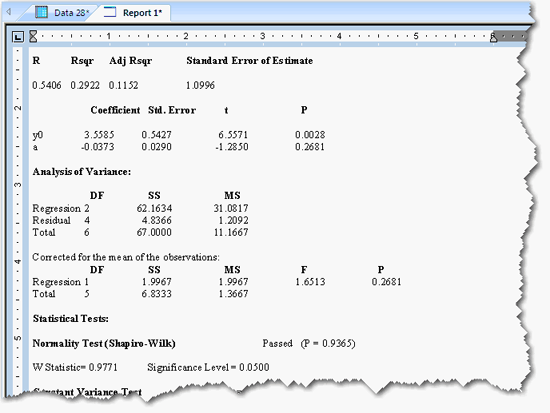 |
重相関係数 (multiple correlation coefficient) R と決定係数 (coefficient of determination) R2 は、いずれも回帰モデルがどれだけうまくデータを説明しているかを評価する指標です。R 値が 1 に近いほど、その方程式が独立変数と従属変数の間の関係をうまく説明していることをあらわします。独立変数の値から従属変数の値を全く予測できないときは、R が 0 となります。また、独立変数から従属変数を完全に予測できるときは 1 となります。
自由度調整済み決定係数 (adjusted R2, R2adj) も、回帰モデルがどれだけうまくデータを説明しているかを評価する指標ですが、独立変数の数に自由度を反映させます。R2adj の値が大きいほど (1 に近いほど) その方程式が独立変数と従属変数の間の関係をうまく説明していることをあらわします。
推定量の標準誤差 (standard error of the estimate) S y|x は、推定する母集団の回帰平面に対する、実際のばらつきの回帰平面を評価する指標です。推定する母集団は、観測される標本の2標準誤差の範囲におさまるのが一般的です。
標準誤差、t 値および P 値は、回帰分析の反復処理の最後に算出される近似値です。
回帰モデルの定数の値と独立変数の係数 (coefficient) がリストで表示されます。
漸近的標準誤差は、回帰係数の推定値の不確実性をはかる尺度です (標本平均の標準誤差に似ています)。推定する母集団の真の回帰係数は、予測係数の2標準誤差の範囲内にあるのが一般的です。標準誤差が大きいほど多重共線性 (multicollinearity) を示す可能性が高くなります。デフォルトでは、回帰問題に重み付けがあるか無いかを問わずに標準誤差の計算が行われます。重み付けのない問題の場合、各パラメータの標準誤差には測定データの標準偏差を推定する因数が含まれます。この場合は、全てのデータポイントの誤差のばらつきは等しいものと仮定されます。
重み付けのある問題の場合、標準誤差の計算には2つのオプションがあります。ひとつは、測定データの標準偏差を推定する因子を含んだもので、このオプションを Reduced chi-square と呼びます。もうひとつは、この因子を計算から外したものです。標準誤差のオプションを選択するには、Equation Options ダイアログボックスを開いてください。
t 統計量は、独立変数の係数がゼロである、すなわち、独立変数が従属変数の予測に寄与しないとする帰無仮説を検定します。t は、回帰係数 (regression coefficient) をその標準誤差 (standard error) で割った比です。
![]()
t 値が大きければ、その独立変数を従属変数の予測に使用できる (例えば、係数がゼロではない) と結論づけることができます。
P は、t に関する P 値を計算したものです。P 値は、回帰係数がゼロではないと誤って結論付ける確率です (すなわち、t に基づいて帰無仮説を誤って棄却する、すなわち、第1種の過誤 (Type I error) を犯す確率です)。P 値が小さいほど、係数がゼロでない確率は高くなります。
伝統的に P < 0.05 であれば、独立変数を従属変数の予測に使うことができると結論付けることができます
ANOVA (analysis of variance) テーブルには、回帰分析に関する ANOVA 統計量と、それに対応するステップ毎の F 値がリスト表示されます。
平方和 (SS: Sum of Squares) は、従属変数のばらつきの測度です。
自由度 (DF: Degrees of freedom) は、測定データや回帰方程式の変数の数をあらわします。
平均平方 (MS: Mean Square) は、母分散に関する2つの推定値を求めます。これら2つの分散推定値の比較が分散分析の基礎となります。
Regression (回帰) の平均平方は、従属変数の平均値からの回帰のばらつきの測度です。次式で与えられます:
![]()
残差平均平方 (residual mean square) は、回帰平面に関する残差のばらつきの測度です。次式で与えられます:
![]()
残差平均平方は、S 2y|xとも等しくなります。
F 検定の統計量は、従属変数の予測における独立変数の寄与 (contribution) の尺度です。次の比率で表されます:
![]()
F が大きな値である場合は、独立変数が従属変数の予測に寄与していると結論付けることができます (すなわち、係数の少なくとも1つがゼロでなく、かつ、説明できないばらつき (unexplained variability) が、無作為抽出した従属変数の平均に関するばらつきの期待値より小さい場合) 。F 比が 1 に近いときは、変数間には関連性がないと結論付けることができます (すなわち、このデータは、すべての標本がランダムに分布しているという帰無仮説と合致します)。
P 値は、従属変数と独立変数の間に誤って関連性があると結論付ける確率です (すなわち、F に基づいて帰無仮説を誤って棄却する、すなわち、第1種の過誤 (Type I error) を犯す確率です)。P 値が小さいほど、関連性のある確率が高くなります。
伝統的に P < 0.05 であれば、独立変数を従属変数の予測に使うことができると結論付けることができます。
PRESS (Predicted Residual Error Sum of Squares:予測残差平方和) は、回帰モデルが新規データをどれだけうまく予測できるかを評価する尺度です。PRESS 統計量が小さいほど、そのモデルの予測能力は高いことになります。
PRESS 統計量は、予測誤差 (予測値と実測値の差) の二乗を観測毎に合計して算出します。回帰方程式の計算では、観測したときのデータは除外します。
Durbin-Watson 統計量は、残差間の相関の測度です。残差間に相関がない場合、Durbin-Watson 統計量は 2 になります。この値が 2 から離れるほど、残差間の相関の尤度 (likelihood) は高くなります。
回帰モデルでその残差が互いに独立していると仮定するとき、Durbin-Watson 検定はこの仮説をチェックするのに使用します。Durbin-Watson 値が 2 から 0.50 以上外れる場合、すなわち、Durbin-Watson 統計量が 1.50 より小さいか、2.50 より大きい場合は、レポートに警告が表示されます。
正規性検定 (Normality Test) の結果には、元になる母集団が回帰モデルの周囲に正規分布しているという仮説の検定にそのデータが合格 (Pass) したか否か、および、この検定で算出される P 値が表示されます。すべての回帰モデルは、元になる母集団が回帰線の周囲に正規分布すると仮定します。正規性検定が棄却された場合は、レポートに警告が表示されます。
正規性検定が棄却された場合は、影響力のある外れ値が存在するか、回帰モデルに誤りがある可能性があります。
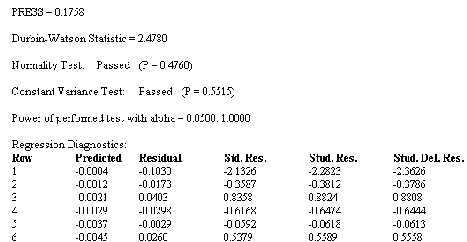 |
等分散検定 (Constant Variance Test) の結果には、元になる母集団の従属変数のばらつきが独立変数の値にかかわらず一定であるという仮説の検定にそのデータが合格 (Pass) したか否か、およびこの検定で算出される P 値が表示されます。等分散検定が棄却された場合は、レポートに警告が表示されます。
等分散検定が棄却された場合、重み付き回帰を使用する別のモデルの使用 (例えば、データの形状により近いモデル)、または、独立変数を変換してばらつきを安定化し、より精度の高い回帰方程式のパラメータ推定値を得ることを検討してください。
重み付き回帰モデルを実行する場合、正規性と等分散の検定では行の残差
![]()
を使う代わりに、重み付き残差
![]()
を使用します。
回帰モデルの検出力 (Power)、すなわち感度は、そのモデルに変数間の関連性がある場合に、それらの関係をモデルが正しくあらわす可能性をはかる尺度です。
回帰モデルの検出力は、測定データの数、異なる有意水準を誤ってレポートする危険性、回帰式の傾きに影響を受けます。
アルファ (α) は、そのモデルが本当は誤っているのに正しいと結論付けてしまうことを許容する確率です。アルファ (α) の誤りを、第1種の過誤 (Type I error) と呼ぶこともあります (第1種の過誤は、関係がないという仮説が真であるのに、棄却してしまう場合です)。
アルファ (α) の値が小さくするほど、そのモデルが正しいと結論付ける要件はより厳密になりますが、反対に、そのモデルが実際は正しいにもかかわらず誤りであると結論づけてしまう可能性は高くなります (第2種の過誤)。値を大きくしてモデルを正しいと結論付ける条件を緩和すると、誤ったモデルを採用してしまう危険率も高くなります (第1種の過誤)。
回帰診断 (regression diagnostic) の結果では、予測された値、残差、その他の診断結果が表示されます。
これは、測定データの行番号です。
これは、各測定データについて、回帰モデルによって予測された従属変数の値です。
従属変数に関する測定値と予測値の差で、重み付けのされていない生の残差です。
標準化残差 (Standardized Residuals) は、生の残差を推定量の標準誤差 S y|x で割ったものです。残差が回帰モデルの周囲に正規分布していれば、標準化残差の約 66% は、-1 から +1 の間の値をとり、標準化残差の約 95% は、-2 から +2 の間の値をとります。標準化残差の値が大きいほど、その点は回帰モデルから離れていることを示します。値が -2.5 より小さい場合、もしくは、2.5 より大きい場合は、そのケースが外れ値である可能性があります。
スチューデント化残差 (Studentized residual) は、従属変数の予測値の信頼性についてデータセットの中央を高く考慮する標準化残差です。極端なデータポイント (独立変数の最小値と最大値を持つデータポイント) の残差の値に重みを付けることによって、標準化残差に比べて外れ値の検出の感度が高くなります。この残差は、全データを使って推定量の標準誤差を計算することから、内部スチューデント化残差とも言われています。
外部スチューデント化残差 (externally Studentized residual) とも言われる、スチューデント化削除残差 (Studentized deleted residual) は、推定量の標準誤差 Sy|x(-i)を使用し、この残差に関係するデータポイントを削除した後に計算を行うスチューデント化残差です。分散の計算からこのデータポイントを削除することによって、外れ値に対する影響が大きくなります。
スチューデント化削除残差は、スチューデント化残差よりも外れ値に対して遥かに大きな値を算出するので、スチューデント化残差に比べて外れ値の検出の感度が高くなります。
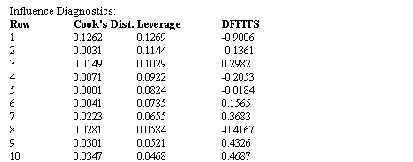
これは、測定データの行番号です。
クックの距離 (Cook’s Distance) は、回帰方程式のパラメータ推定において各点が有する影響力の大きさを評価する尺度です。これは、評価する点を分析から除外したとき回帰係数の値がどれだけ変化するかをはかるものです。
値が 1 より大きい場合は、その点に影響力がある可能性を示します。クックの距離が 4 より大きい場合、その点は、パラメータ推定値に対して大きな影響があることを示します。
レバレッジ (Leverage:てこ比) の値は、影響力をもつ可能性のある点を識別します。観測データのレバレッジが期待されるレバレッジより2倍以上大きい場合は、その点に影響力がある可能性があります。
データポイントの期待レバレッジは、p /n であらわされます。ここで、p はパラメータ数、n はデータポイント数です。
レバレッジの計算には従属変数しか使用しませんので、独立変数の極値 (大きい値と小さい値) がレバレッジの高い点になる傾向があり、このような点では、独立変数のわずかな変化が従属変数の予測値に大きな影響を与える可能性があります。
DFFITSi 統計量は、回帰予測におけるデータポイントの影響力の測度です。i 番目の DFFITS は、あるデータポイントに関して、回帰係数を計算する前にその測定値をデータセットから除外したときの標準誤差の違いを推定した数です。ある予測値について、そのデータポイントを除外したときの標準誤差が 2.0 より大きくなる場合、その予測値には、潜在的に影響力があります。
 |
両区間の信頼水準 (confidence level) のデフォルト値は 95% に設定されています。この値は、Report Options for Nonlinear Regression ダイアログで変更することができます。
予測値に関する信頼区間は、その従属変数の母集団平均が一定の可能性 (probability) で存在する値の範囲を定義します。この可能性を、信頼水準 (confidence level) といいます。
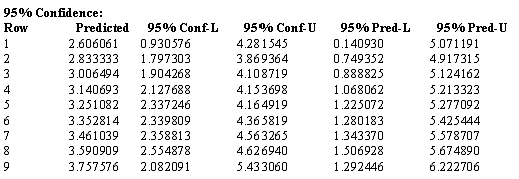 |
これは、測定データの行番号です。
この列は回帰モデルによって予測される測定毎の従属変数の値をあらわします。
回帰モデルの信頼区間は、特定の信頼水準における従属変数と独立変数の間の真の関連性が含まれる領域を、計算で求めた変数値の範囲で与えます。95% Conf-L の値は下限 (lower limits) を、95% Conf-U の値は上限 (upper limits) をあらわします。
母集団の信頼区間は、特定の信頼水準において、測定データが存在する可能性のある母集団が含まれる領域を、計算で求めた変数値の範囲で与えます。95% Pred-L の値は下限 (lower limits) を、95% Pred-U 値は上限 (upper limits) をあらわします。