13.11 F Test Comparison of Curves

F Test Comparison of Curves マクロを使用すると、2つの方程式のあてはまりを比較して、より複雑な方程式のほうが有意によくあてはまるかどうかを決定することができます。検定を有効にするには、2つの方程式がネストされていなければなりません。つまり、単純な方程式は、さらに複雑な方程式の一部 (サブセット) である必要があります。

F 検定は、より単純な方程式が正しいという帰無仮説からなる仮説検定です。F 比は自由度の相対的増加に対する 2つのフィッティングの平方和の相対的差異を比較して計算されます。この値が 1.0 よりも有意に大きい場合、帰無仮説は棄却され、さらに複雑な方程式が最適なフィッティングとして採択されます。P 値は、F 値が 1.0 よりも有意に大きいかどうか判断するために使用されます。P < 0.05 の場合、帰無仮説は棄却され、さらに複雑なモデルが適していると見なされます。

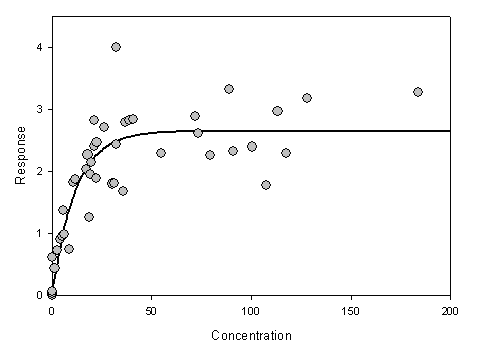
次の例では、最大値に向けた単一指数関数的増加よりも、二重指数関数的増加の方程式のほうが、あてはまりがより優れているかを判断します。

 

最大値への単一指数関数的増加 (Single Exponential Rise to Maximum)

最大値への二重指数関数的増加 (Double Exponential Rise to Maximum)

上記２つの方程式を以下に示すグラフのデータにあてはめると、平方和と自由度はいずれも相対的に増加します。

平方和の相対的増加

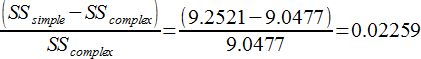
自由度の相対的増加

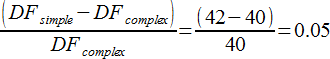
これら２つの比から F 比が求められます：

P 値は F 分布から計算され、P=0.65 となります。

 

はじめに単純な方程式を、次に複雑な方程式をあてはめると、マクロにより F-test Comparison of Curves ダイアログボックスのすべてのオプションが選択されます。

 

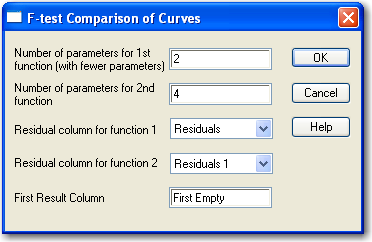そうでない場合、方程式のパラメータの数 (単純な方程式を最初に) 、および、方程式のあてはめの残差を格納した列をそれぞれ手動で入力することができます。

結果はレポートに示されます。