 |
| サイトマップ | |
|
 |
| サイトマップ | |
|
この方程式は、特異的結合のデータ (y) がリガンド濃度 (x) の関数であるとして当てはめるのに使用します。SigmaPlot ディレクトリの SigmaPlot Macro Library.jnb (※注:現行では、Macro Data Sets.jnb) ファイルにはサンプルデータセット "One site saturation – 2 replicates" が用意されています。
![]()
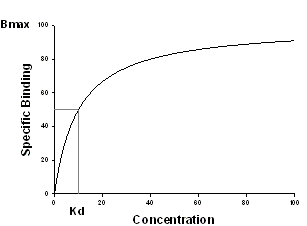
| Variable | Range | Definition | Units |
|---|---|---|---|
| x | >= 0 | 遊離リガンドの濃度 | concentration, M |
| y | >= 0 | 特異的結合 (=全結合 - 非特異的結合) | cpm, sites/cell, fmol of receptor/mg of tissue |
| Bmax | > 0 | 結合部位の最大数 | same as y |
| Kd | > 0 | 平衡解離定数:最大結合の半分に達するリガンドの濃度 | concentration |
この方程式は、親和性の異なる2つの受容体の結合部位を考慮します。
![]()
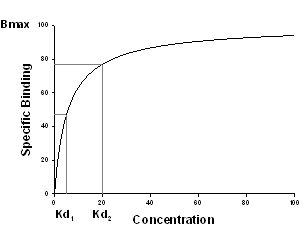
| Variable | Range | Definition | Units |
|---|---|---|---|
| x | >= 0 | 遊離リガンドの濃度 | concentration, M |
| y | >= 0 | 特異的結合 (=全結合 - 非特異的結合) | cpm, sites/cell, fmol of receptor/mg of tissue |
| Bmax 1 | > 0 | 受容体 1 に関する結合部位の最大数 | same as y |
| Bmax2 | > 0 | 受容体 2 に関する結合部位の最大数 | same as y |
| Kd1 | > 0 | 受容体 1 に関する平衡解離定数 | concentration |
| Kd2 | > 0 | 受容体 2 に関する平衡解離定数 | concentration |
この方程式は、全結合濃度 (y) がリガンド濃度 (x) の関数であるとして当てはめるのに使用します。one site saturation 方程式にはないパラメータ N は、非特異的 (nonspecific) 結合を考慮するものです。3パラメータの推定量を良いものにするには、それだけ多くのデータポイントが必要になります。
![]()
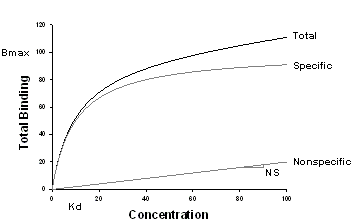
| Variable | Range | Definition | Units |
|---|---|---|---|
| x | >= 0 | 遊離リガンドの濃度 | concentration, M |
| y | >= 0 | 全結合 | cpm, sites/cell, fmol of receptor/mg of tissue |
| Bmax | > 0 | 結合部位の最大数 | same as y |
| Kd1 | > 0 | 平衡解離定数:最大結合の半分に達するリガンドの濃度 | concentration |
| N | > 0 | 非特異的結合直線の傾き | y units/x units |
この方程式は、データが受容体の結合部位の存在を2つサポートする場合に、全結合濃度 (y) をリガンド濃度 (x) の関数として当てはめるのに使います。この方程式には、5つのパラメータがありますので、これらのパラメータを精確に推定するには十分な数のデータポイントが必要となります。
![]()
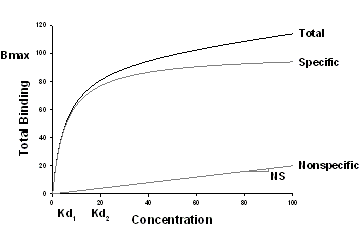
| Variable | Range | Definition | Units |
|---|---|---|---|
| x | >= 0 | 遊離リガンドの濃度 | concentration, M |
| y | >= 0 | 全結合 | cpm, sites/cell, fmol of receptor/mg of tissue |
| Bmax1 | > 0 | 受容体 1 に関する結合部位の最大数 | same as y |
| Bmax2 | > 0 | 受容体 2 に関する結合部位の最大数 | same as y |
| Kd1 | > 0 | 受容体 1 に関する平衡解離定数 | concentration |
| Kd2 | > 0 | 受容体 2 に関する平衡解離定数 | concentration |
| N | > 0 | 非特異的結合直線の傾き | y units/x units |
この方程式は、用量-応答 (dose-response) の典型的な関係を説明するものです。薬物データ x は、対数形式で入力します。y 変数は応答です。EC50 は、y の最小値 (min) と最大値 (max) の半分にあたるの薬物濃度です。
![]()
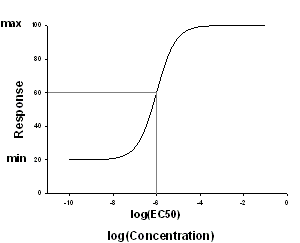
| Variable | Range | Definition | Units |
|---|---|---|---|
| x | > 0 | 対数薬物濃度 | log concentration, log(M) |
| y | >= 0 | 応答 | response units |
| min | > 0 | 応答の最小平坦域 | same as y |
| max | > 0 | 応答の最大平坦域 | same as y |
| logEC50 | > 0 | EC50 または IC50 の対数 | log concentration |
この方程式は、用量-応答 (dose-response) の典型的な関係を説明するものですが、その中間点における曲線の傾きを特徴付けるパラメータ、Hillslope (ヒル勾配) が加わる点が異なります。薬物データ x は、対数形式で入力します。Hillslope = 1.0 のとき、この方程式はシグモイド型の用量-応答曲線と同じになります。また、勾配パラメータの符号が逆向きであることを除けば、4つのパラメータのロジスティック関数 (four-parameter logistic function) とも同じになります。
![]()

| Variable | Range | Definition | Units |
|---|---|---|---|
| x | > 0 | 対数薬物濃度 | log concentration, log(M) |
| y | >= 0 | 応答 | response units |
| min | > 0 | 応答の最小平坦域 | same as y |
| max | > 0 | 応答の最大平坦域 | same as y |
| logEC50 | > 0 | EC50 または IC50 の対数 | log concentration |
| Hillslope | all | 曲線の傾きに関連。>0 のとき曲線は x と共に増加。 | unitless |
競合研究では、ある受容体と既に結合しているリガンドと競合するリガンドを追加します (2つのリガンドは同じであると推定されます)。リガンドを追加してゆけば、既に結合済みのリガンドの量は減少します。One Site Competition 方程式は、リガンドの追加に伴うこの減少を特徴付けるものです。薬物データ x は、対数形式で入力します。この方程式は、指数の符号が変わることを除けば、Sigmoidal Dose-Response 方程式と同じです。シグモイド型の用量-応答方程式は x と共に増加しますが、one site competition では x と共に減少します。SigmaPlot ディレクトリの SigmaPlot Macro Library.jnb ファイルには、"One site competition – 3 replicates" というタイトルのサンプルデータセットが用意されています。
![]()
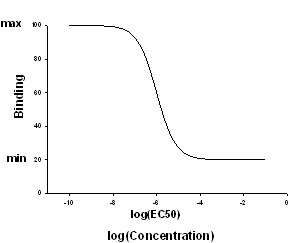
| Variable | Range | Definition | Units |
|---|---|---|---|
| x | > 0 | 対数薬物濃度 | log concentration, log(M) |
| y | >= 0 | 全結合または特異的結合 | cpm, % specific binding, sites/cell, fmol of receptor/mg of tissue |
| min | > 0 | 非特異的結合 | same as y |
| max | > 0 | Cold リガンドが存在しない場合の最大結合数 | same as y |
| logEC50 | > 0 | EC50 または IC50 の対数 | log concentration |
この方程式は、リガンドが2つの受容体と結合する競合研究に使用します。薬物データ x は、対数形式で入力します。
![]()
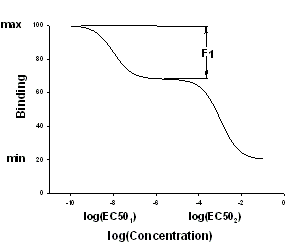
| Variable | Range | Definition | Units |
|---|---|---|---|
| x | > 0 | Cold リガンドの対数濃度 | log concentration, log(M) |
| y | >= 0 | 全結合または特異的結合 | cpm, % specific binding, sites/cell, mol of receptor/mg of tissue |
| min | > 0 | 非特異的結合 | same as y |
| max | > 0 | Cold リガンドが存在しない場合の最大結合数 | same as y |
| F1 | > 0 | 親和性が logEC501 の受容体の占める比率 | unitless |
| LogEC501 | > 0 | EC501 または IC501 の対数 | log concentration |
| LogEC502 | > 0 | EC502 または IC502 の対数 | log concentration |
この関数は、標準曲線 (standard curves)、放射免疫測定 (ラジオイムノアッセイ radioimmunoassays)、および、用量-応答曲線で最も良く利用されるものです。ここに含まれるパラメータは、これらの分野で一般に利用される A, B, C, D という標準記号のみであらわされます。 薬物データ x は、対数形式で入力します。勾配パラメータの符号の違いを除けば、シグモイド型の用量-応答 (variable slope) 方程式と全く同じです。
![]()
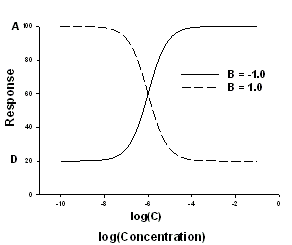
| Variable | Range | Definition | Units |
|---|---|---|---|
| x | > 0 | 薬物、用量の対数濃度 | log concentration, log(M) |
| y | >= 0 | 応答 | response units |
| D | > 0 | 応答の最小平坦域 | same as y |
| A | > 0 | 応答の最大平坦域 | same as y |
| logC | > 0 | EC50 または IC50 の対数 | log concentration |
| B | all | 曲線の傾きと関連する。<0 のとき曲線は x と共に増加。 | unitless |
これは、用量濃度 (x データ) を線形形式でワークシートに入力することを除けば、four-parameter logistic equation と同じです。この方程式と four-parameter logistic equation で得られるカーブフィットの結果は、全く同じです。この方程式を使う唯一の理由は、X 軸のスケールが線形のグラフを作成したいときです。log(x) データを使って four-parameter logistic equation を当てはめたあと、X 軸のスケールを線形に変更すると、当てはめラインの精度が悪くなります。この方程式を使えば、この精度の問題が解消されます。
![]()
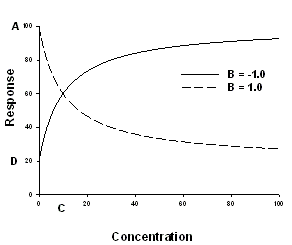
| Variable | Range | Definition | Units |
|---|---|---|---|
| x | > 0 | 薬物、用量の対数濃度 | log concentration, log(M) |
| y | >= 0 | 応答 | response units |
| D | > 0 | 応答の最小平坦域 | same as y |
| A | > 0 | 応答の最大平坦域 | same as y |
| logC | > 0 | EC50 または IC50 の対数 | log concentration |
| B | all | 曲線の傾きと関連する。<0 のとき曲線は x と共に増加。 | unitless |
これは、ある方程式を編集してパラメータのひとつを定数 (max=100) に固定する方法を示す事例です。この方程式の説明は、パラメータ max を当てはめに使わず 100 に固定することを除けば、One Site Competition と同じです。他の方程式でこれ以外のパラメータの組合せを固定する方法に関する詳細は、方程式に定数を設定するをご覧ください。SigmaPlot ディレクトリの SigmaPlot Macro Library.jnb ファイルにには、"One site competition – 3 replicates" というタイトルのサンプルデータセットが用意されています。
これは、ある方程式を編集して2つのパラメータを定数に固定する方法 (min = 0 と max = 100) を示す2つ目の事例です。この方程式の説明は、パラメータ min と max を当てはめに使わずそれぞれ 0 と 100 に固定することを除けば、One Site Competition と同じです。他の方程式でこれ以外のパラメータの組合せを固定する方法に関する詳細は、方程式に定数を設定するをご覧ください。SigmaPlot ディレクトリの SigmaPlot Macro Library.jnb ファイルにには、"One site competition – 3 replicates" というタイトルのサンプルデータセットが用意されています。