SigmaPlot 基本操作ガイド - 対応のある 2 標本の t 検定

SigmaPlot による対応のある 2 標本の t 検定に関する使用例を説明いたします。

• t 検定とは
• 対応のない 2 標本の t 検定 (t-Test) とは
• 対応のある 2 標本の t 検定 (Paired t-Test) とは
• 補足
• 例題 対応のない 2 標本の t 検定
• 例題 対応のある 2 標本の t 検定

 

例題 対応のある 2 標本の t 検定

次の例題について、SigmaPlot を使用し対応のある 2 標本の t 検定を実施する手順を紹介します。

部品製造装置の製造工程を見直すことで製造部品の精度に影響があると言えるか調べたいと思います。従来の製造工程で製造した部品と製造工程を変更して製造した部品を各々 8 つサンプリングし、対応のある t 検定を実施します。

表1

従来の製造工程の部品	製造工程を変更した部品
1.12	1.20
1.09	0.91
1.16	1.25
1.13	1.23
1.08	1.17
1.08	1.12
1.03	0.94
1.11	1.05

 

操作手順

SigmaPlot の Σ メニューをクリックして New → Notebook を実行しワークシート (Data 1) を表示します。

 

下図のようにワークシートにデータを入力します。

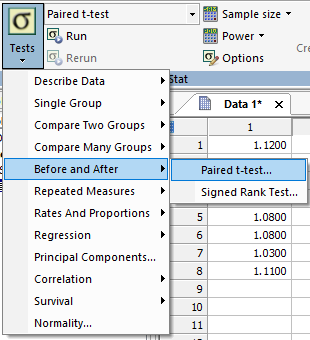
続いて Analysis タブ→ Tests → Before and After → Paired t-test... を実行します。

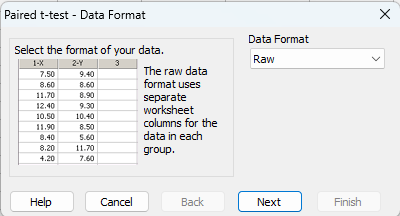
Raw 形式のまま、Next ボタンをクリックします。

ワークシートから変数を選択して (もしくは Data for Data プルダウンメニューから各々の変数を選択して) 変数を割り当てます。

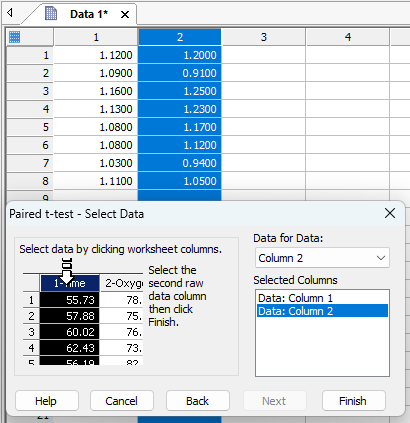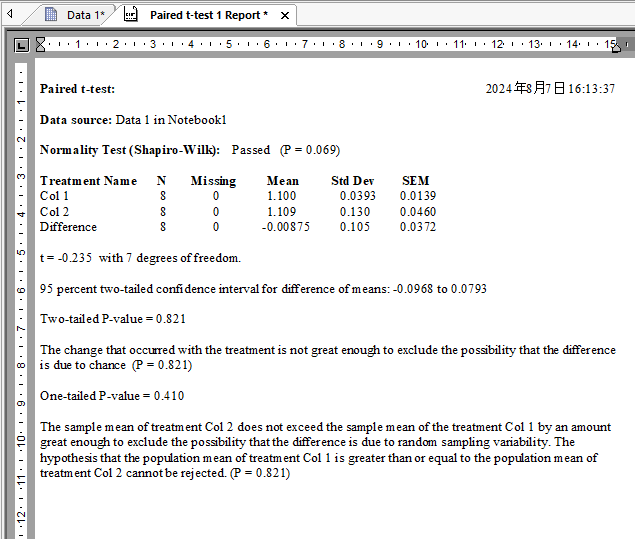
Finish ボタンをクリックします。対応のある t 検定 のレポートが出力されます。

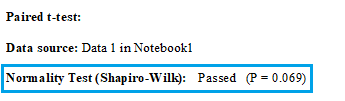
正規性の検定 (Shapiro-Wilk) の帰無仮説と対立仮説は次のとおりです。

帰無仮説: データは正規分布に従う 対立仮説: データは正規分布に従わない

有意水準 (帰無仮説を棄却するかを判断する基準となる確率) は α=0.05 としています。

正規性の検定 (Shapiro-Wilk) は、「Passed」と表示されています。P 値は有意水準 0.05 より大きく帰無仮説は棄却されず、2つの標本は正規性を満たしていると言えます。

対応のある t 検定の結果は、t 値が自由度 7 の -0.235 で、両側検定の P 値 (Two-tailed P-value) は 0.821 と α=0.05 より大きい値で帰無仮説は棄却されません。従来の製造工程で製造した部品と製造工程を変更して製造した部品の精度に差はないと言えます。オプションの設定により、レポートには、片側検定の P 値 (One-tailed P-value) も同時に出力されます。

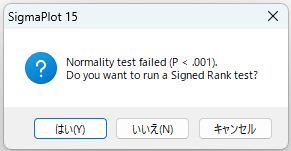
データが正規性を満たしていない場合は、SigmaPlot のアドバイザー機能により Wilcoxon の符号順位検定 (Signed Rank test) の実施を促されます。