SigmaPlot 基本操作ガイド - 対応のない 2 標本の t 検定

SigmaPlot による対応のない 2 標本の t 検定に関する使用例を説明いたします。

• t 検定とは
• 対応のない 2 標本の t 検定 (t-Test) とは
• 対応のある 2 標本の t 検定 (Paired t-Test) とは
• 補足
• 例題 対応のない 2 標本の t 検定
• 例題 対応のある 2 標本の t 検定

 

例題 対応のない 2 標本の t 検定

次の例題について、SigmaPlot を使用し対応のない 2 標本の t 検定を実施する手順を紹介します。

部品製造装置のリプレイスを検討しています。現在使用している装置 A と海外メーカーの装置 B を比較したいと思います。

装置 A と装置 B で製造した部品を各々 8 つサンプリングし、基準値からの誤差を測定しました。装置 A と装置 B の製造部品の加工精度の違いを推定します。

表1

装置 A	装置 B
0.0013	0.0020
0.0002	0.0021
0.0016	0.0025
0.0014	0.0030
0.0008	0.0017
0.0007	0.0012
0.0005	0.0022
0.0011	0.0019

 

操作手順

SigmaPlot の Σ メニューをクリックして New → Notebook を実行しワークシート (Data 1) を表示します。

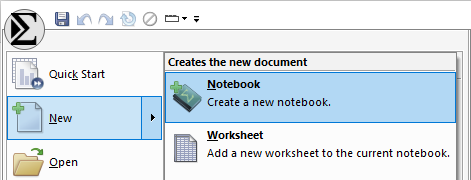下図のようにワークシートにデータを入力します。

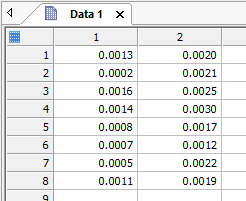続いて Analysis タブ→ Tests → Compare Two Groups → t-test... を実行します。

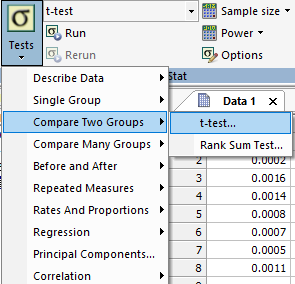Raw 形式のまま、Next ボタンをクリックします。

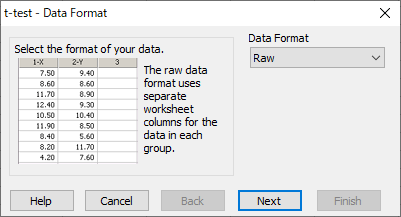ワークシートから変数を選択して (もしくは Data for Data プルダウンメニューから各々の変数を選択して) 変数を割り当てます。

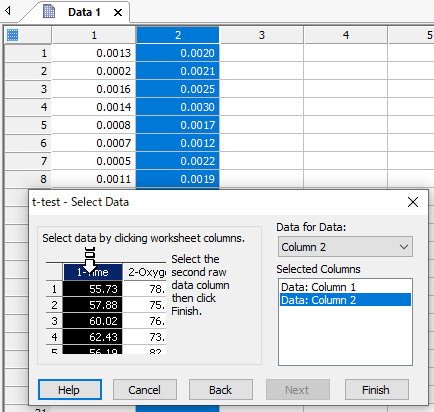Finish ボタンをクリックします。t 検定 のレポートが出力されます。

正規性の検定 (Shapiro-Wilk) の帰無仮説と対立仮説は次のとおりです。

帰無仮説: データは正規分布に従う 対立仮説: データは正規分布に従わない

等分散性の検定 (Brown-Forsythe) の帰無仮説と対立仮説は次のとおりです。

帰無仮説: 2 つの分散は等しい 対立仮説: 2 つの分散は等しくない

有意水準 (帰無仮説を棄却するかを判断する基準となる確率) は α=0.05 としています。

正規性の検定 (Shapiro-Wilk) 及び等分散性の検定 (Brown-Forsythe) は、いずれも「Passed」と表示されています。P 値は有意水準 0.05 より大きく帰無仮説は棄却されず、2つの標本は正規性ならびに等分散性を満たしていると言えます。

t 検定の結果は、t 値が自由度 14 の -4.428 で、両側検定の P 値 (Two-tailed P-value) は 0.000573 と α=0.05 より小さい値で帰無仮説は棄却され対立仮説が採択されます。装置 A と装置 B の製造部品の加工精度には違いがあると言えます。 (オプションの設定により、レポートには、片側検定の P 値 (One-tailed P-value) も同時に出力されます。)

もしデータが等分散性を満たしていない場合は、レポートに出力されているウェルチの t 検定の結果を確認します。ここでは両側検定の P 値 (Two-tailed P-value) は 0.000588 と α=0.05 より小さい値で帰無仮説は棄却され対立仮説が採択されます。
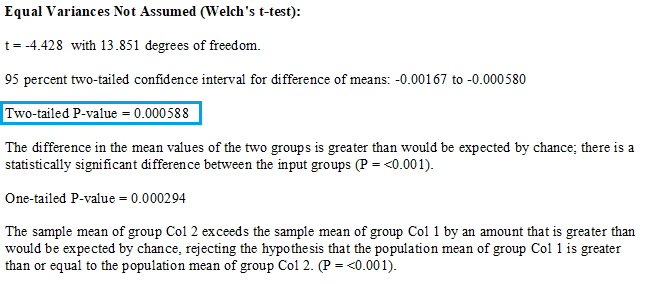