 |
| サイトマップ | |
|
 |
| サイトマップ | |
|
SigmaPlot による t-検定に関する使用例を説明いたします。
t 検定 (スチューデントの t 検定) は、統計的仮説検定の手順で t 分布を用いる検定法の総称です。t 検定には、対応のない2 標本の t 検定と対応のある 2 標本の t 検定があります。
対応のない 2 標本の t 検定は、2つの独立した母集団から抽出した標本の平均に差があるかどうかを検定します。SigmaPlot の対応のない 2 標本の t 検定の統計量は次の比であらわされます。
t 分布の帰無仮説の棄却域は、両側検定または片側検定と有意水準 (α=0.05 など) に基づいて決定されます。下図は両側検定の棄却域の例を示しています。
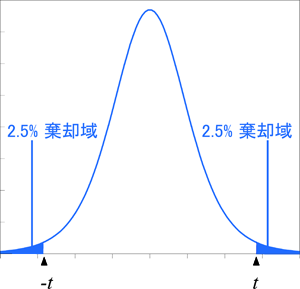 |
2 標本の t 検定における帰無仮説は「2 つの標本の母平均は等しい」で、対立仮説は「2 つの標本の母平均は等しくない」です。
| H0: μ1 = μ2 | (2 つの標本の母平均は等しい) |
| H1: μ1 ≠ μ2 | (2 つの標本の母平均は等しくない) |
標本 1 の母平均が標本 2 の母平均より大きい (または小さい) ことに興味がある場合は、片側検定を実施します。
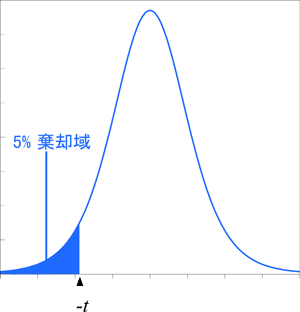
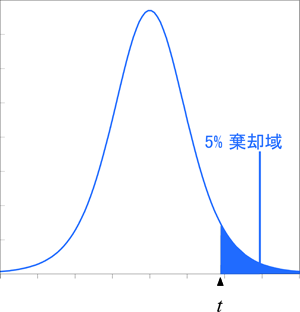
片側検定における帰無仮説は「標本 1 の母平均は標本 2 の母平均と同じか小さい (もしくは大きい)」で、対立仮説は「標本 1 の母平均は標本 2 の母平均より大きい (もしくは小さい)」です。
| 下側 | 上側 | ||||
 |
 |
||||
|
|
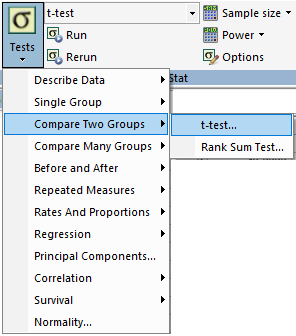
SigmaPlot では、対応のない 2 標本の検定 (各々独立したデータ) は t-test を実行します。対応のない t 検定の操作例はこちらを御覧ください。
 |
対応のある 2 標本の t 検定は、2 つの母集団の間に対応関係がある場合に、2 つの母平均が同じか否かを調べます。
t 検定の統計量は、実験対象のそれぞれについて処理後に測定された値から処理前の値を差し引いて算出します。残りの分析は、これらの差について実施します。SigmaPlot の 対応のある 2 標本の t 検定の統計量は次の比であらわされます。
t の絶対値が大きければ (~2 より大きい)、その処理は関心のある変数に影響を及ぼしていると判断することができます (差はないという帰無仮説は棄却されます)。t の値が大きいものであれば、処理前と処理後の測定値の差が効果のばらつきだけから期待される差よりも大きい (その効果が統計的に有意である) ことを示します。t の値が小さければ (殆ど 0 に近い場合)、標本間に有意差はない (処理前と処理後の平均値の差は殆どない) ことを示します。
対応のある 2 標本の t 検定の帰無仮説は「対応のある 2 つの標本間に平均値の差はない」で、対立仮説は「対応のある 2 つの標本間に平均値の差がある」です。
| H0: μ2 - μ1 = 0 | (対応のある 2 つの標本間に平均値の差はない) |
| H1: μ2 - μ1 ≠ 0 | (対応のある 2 つの標本間に平均値の差がある) |
 |
片側検定は、従来の手法より新しい手法のほうが優れているといった一方向の効果を検証する場合に使用されます。
| 下側 | 上側 | ||||
 |
 |
||||
|
|
SigmaPlot では、対応のある 2 標本の検定 (2 つの母集団の間に対応関係がある。例: 処置前後の変化) は Paired t-test を実行します。対応のある t 検定の操作例はこちらを御覧ください。
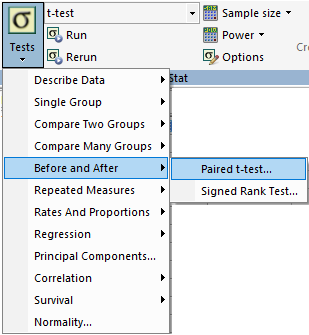 |
SigmaPlot における 2 標本の比較のフローと検定手法の関係は次のとおりです。
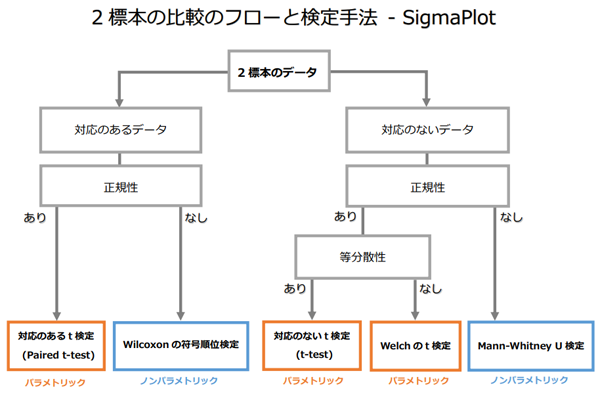 |
ウェルチの t 検定は、スチューデント t 検定を改良したもので、2 つの標本が等分散性を満たしておらず、サンプルサイズが等しくない場合に信頼性が高いとみなされます。
SigmaPlot では、シャピロ・ウィルク検定またはコルモゴロフ–スミルノフ検定を使用して、母集団の正規性を検定します。
(シャピロ=ウィルクの W 統計量は、データが正規分布から抽出されたものであるという帰無仮説を検定します。W 統計量が小さければ、正規性から外れていることを示します。コルモゴロフ–スミルノフ距離は、データのサンプル累積分布関数と、データの平均と分散の推定値に基づく正規分布の累積分布関数との間の最大距離です。)
検定によって計算された P 値がオプションで設定された P 値より大きい場合、データは正規性があるとみなすことができます。下図は t 検定のオプション画面です。
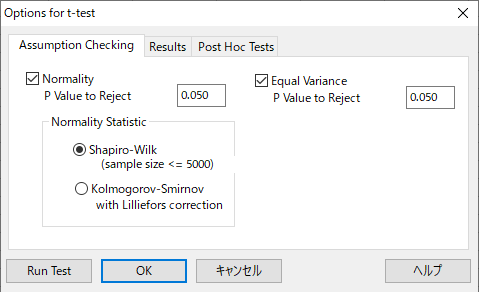 |
SigmaPlot には、等分散性の検定としてブラウン・フォーサイス検定が用意されています。ブラウン・フォーサイス検定は、2群以上の分散の等質性を検定します。ブラウン・フォーサイス検定は、異なるサンプルサイズや異なる分散を持つグループ間のデータに対しても頑健であり、非正規分布に対しても有効であるため幅広いデータの解析に適しています。