|
| サイトマップ | |
|
 |
| サイトマップ | |
|
![]() サンプルデータ:
サンプルデータ:
三角形の各辺の長さを a, b, c とするとき、その面積と外接円の半径を測定してください。
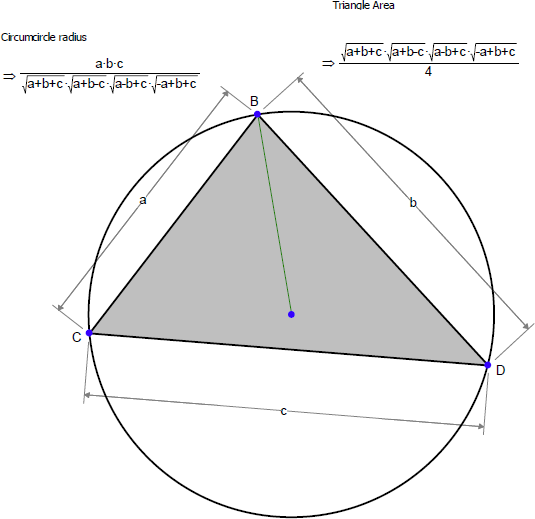
面積と半径はどのような関係になるでしょうか?
三角形が2つの辺とその間に挟まれた角で定義される場合、その面積はどうなるでしょうか?
ここから、外接円の半径の式を角度を使って求めなさい:
Geometry Expressions では以下のようになっているはずです:
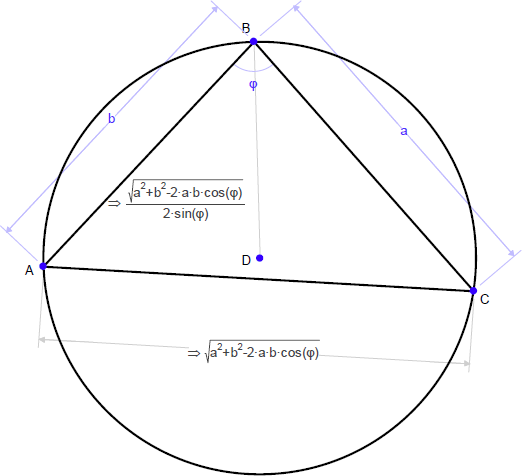
この式が Geometry Expressions を使わずに真であることを証明できるでしょうか?ヒント:以下の図で |BC| の式を求めます。
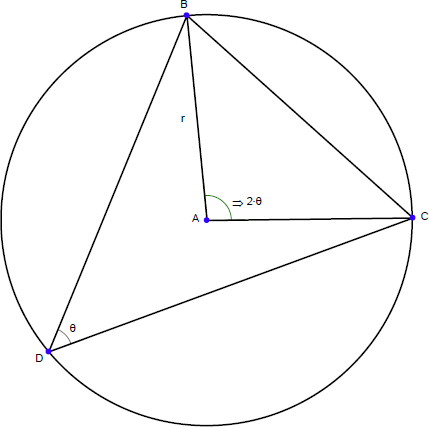
外接円の半径を R とし、三角形の角を A, B, C とし、その対辺の長さを a, b, c とします。この時点で、以下を証明できるはずです:
![]()
![]()
ゆえに
![]()
次に、R に関する最初の式を a, b, c を使って証明するのに必要なことは、Geometry Expressions で作成した三角形の面積の式を証明するだけです (さもなくば、証明なしに受け入れます)。
何の根拠もなしに、ものごとを受け入れようとは思いませんよね。
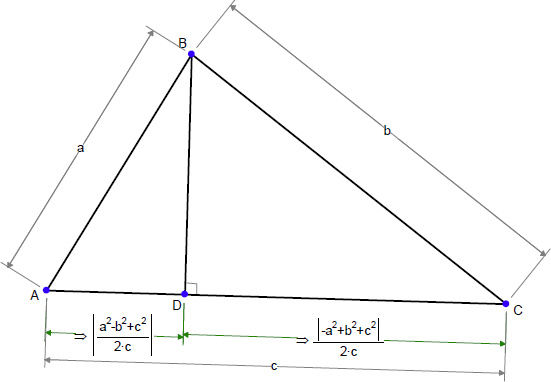
上記は、|AD| と |CD| の値を示したものです。
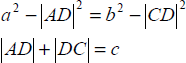
AD の式をお持ちの代数システムにコピーします。次に、高さの二乗の式を作成します。これに c の二乗を掛けて、4 で割ることで、面積の二乗の式が作成されます:
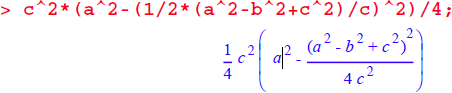
代数的な操作をこれに加えることで、次式が得られます。
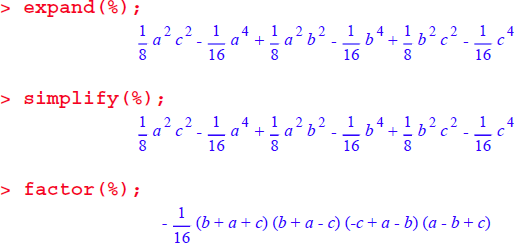
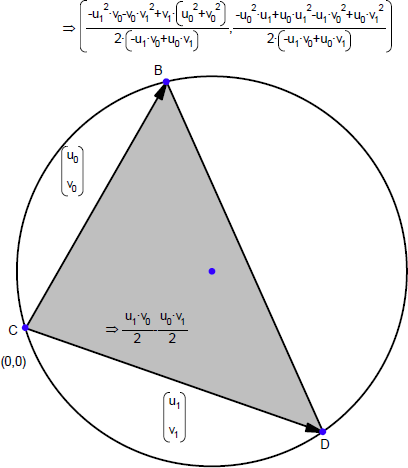
最後の練習問題として、三角形の頂点の座標を使って外接円の中心 (重心座標) を検討することにしましょう。
この式は、非常に複雑ですが、幾つかの要素に分解できます。式の中に面積が埋め込まれているのにお気づきでしょうか?
この内容をベクトルを使ってもっと簡単にあらわすことができますか?