例３：三角測量

サンプルデータ：

• Example_2a.gx

Geometry Expressions には、主に幾何学的問題で登場する数式を操作するために特別に用意された独自の代数システムが装備されています。しかし、幾何学表現の分析を更に踏み込んで進めるには、より完備された代数システムにそれらをコピーして行います。Geometry Expressions では、数式を表示したり計算することができる様々なアプリケーションのインプットデータとして広く利用できる MathML 形式で数式をエクスポートすることができます。

この練習問題では、代数システムにコピーすることで分析を達成する事例を検討することにします。

三角測量を実行するコンピュータープログラムを記述するとします：三角形の底辺の長さと、底辺から頂点に向かう２つの角度が与えられると、プログラムはその頂点の座標を求めます。必要な数式は以下のように Geometry Expressions で生成されます：

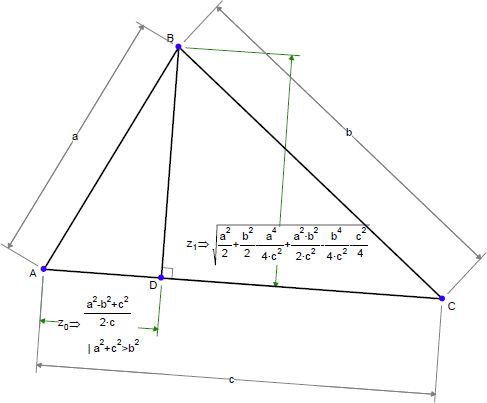
我々がコンピュータープログラムで知りたいのは、計算で求められる量の誤差が測定量 a および b の誤差と比例しているかということです。

a の誤差 δa による z₀ の誤差は近似的に以下のようにあらわせます：

これは、z₁ の誤差についても同様です。

量　 は、誤差の拡大鏡と考えることができます。

式 z₀ を選択すると、その内容を代数システム (Maple、Mathematica など MathML を取り込むことができるよう設計されている任意のシステム) にコピー＆ペーストすることができます。ここでは、 Casio ClassPad Manager を使うことにします。代数システムに移ったら、a について微分を行い、誤差の拡大鏡に関する式を求めます：

z₀ の誤差の拡大鏡は、a/c と単純な比になります。z₁ に関する拡大鏡は、やや複雑なものになります。平方根の内部にある項を因数分解すると、その内容が明確になります：

a=b+c、または、b=a+c、c=a+b のとき、誤差項の分母がゼロなることがわかります。

幾何学的にこれらの条件を説明することができるでしょうか？

誤差項全体を幾何学的に説明することができるでしょうか？ヒント：分母と三角形の面積を比較します。分子を図の AD の距離と比較します。その長さがより厳密に分子と比例する距離を図中に作成できますか？

次のような問題も考えてもいいでしょう：三角測量に最適な形状とはどのようなものですか？問題を簡単にするために、三角形を二等辺三角形、かつ、a=b=x と仮定しましょう。また、底辺の長さは 1 であると仮定します。

これらの関数をグラフ化すると、x の値が大きいときに最初のドミネイトが、x の値が小さいときに第２のドミネイトがあるの観察できます。

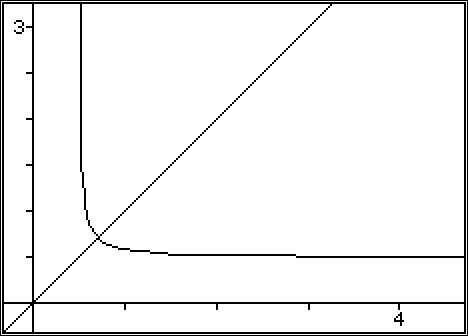
x の最適な値は、この２つが等しくなるときです：

このときの三角形の角度は幾つになりますか？