5. １因子の半折り重ね

「実験をあと８回行えば、仮説を証明できるぞ」とシェリルは宣言します。ランスはため息がちに「やりましょう」と答え、「では具体的にどうやったらいいの？」と返します。「それはね」とシェリルは答えます。「最初にやった２つの実験ブロックと同じポイントを、因子 B についてのみパターンを反転させて試行しましょう。これで、因子 B とその２因子交互作用は、その他の２因子交互作用の影響を受けずに自由になります」。ランスはこれに反論し、「しかし、そうなると実験をあと16回行うことになりませんか」と食い下がります。「ちょっとまって」とシェリルは続けます「以前、Stat‐Ease 社の記事で『How To Save Runs, Yet Reveal Breakthrough Interactions, By Doing Only A Semifoldover On Medium‐Resolution Screening Designs (試行回数を減らしながら、交互作用の問題を打開するには、半折り重ねを中分解能のスクリーニング計画で実行するしかない)』というのを読んだことがあります（参照：statease.com/pubs/semifold.pdf ）。そこには、折り重ねの半分を実行するだけで、2FI を非エイリアス化するという目的を達成できる方法が詳しく書かれていました。結局ランスはトラックをあと８周走るよう言いくるめられたのでした。

試行をさらに追加作成するには、Design‐Expert の “Design” ノードに戻り、メニューから “Design Tools” -> “Augment Design” -> “Augment” を選択します。今度は “Semifold” を実行するようプログラムに忠告が表示されます。

半折り重ねによる試行の増補

 

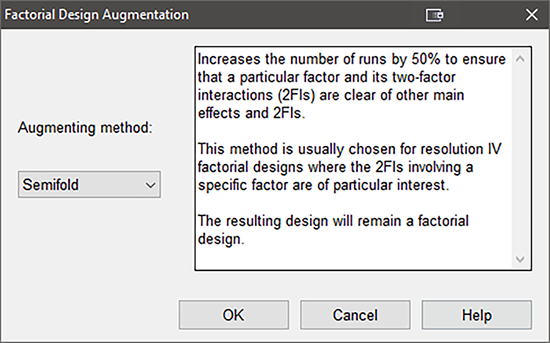“OK” を押すと、これからランスが走ることになる第３ブロックの試行として、どの試行を追加するかを定義するダイアログボックスが表示されます。Choose the factor to fold on フィールドに “B” を指定してください。ランスとシェリルは、次の質問「Choose the factor and its level to retain」に少し頭を悩ませますが、直ちに “D+” 、すなわち、ヘルメットメーカー Windy を選択します。この因子は間違いなく応答に影響を及ぼさないと判断したからです（また、シェリルはこのブランドのヘルメットをランスがかぶっているのを見るのが好きなのです！）。

半折り重ねの指定ダイアログ

 

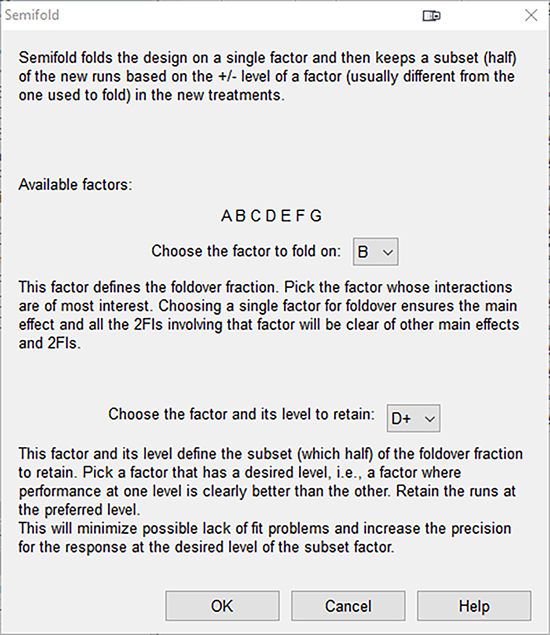ダイアログの “OK” をクリックして、計画評価への移行を了解する “Yes” をクリックしてください。欠損データに関する警告が表示されたら、もう一回 “Yes” をクリックします。現在、Evaluation の開始画面が表示されているはずです。“Results” をクリックして、新たに追加されたエイリアス構造を確認してください。画面を下にスクロールさせて、2FI を表示し、BE が今度は３因子交互作用のみでエイリアス化されていることに注意を払ってください。

半折り重ね後のエイリアス表示

 

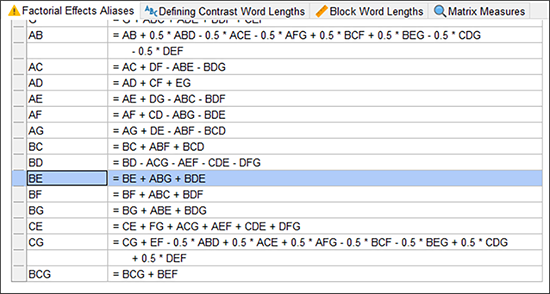例えば AB のように、他の効果が小数点になってエイリアス化されている効果があることに注目してください。これは計画全体を非直交にするために起こる半折り重ねの副産物で、効果をこれ以上独立して評価することはできないことを表しています。後で、このデータを Design‐Expert で分析する際、このことを警告するダイアログが表示されることになります。

メインの “Design” をクリックして、増補された試行を確認してください。Std 列のヘッダーをダブルクリックして、その並びを標準の順序に戻します。

ランスが第３ブロックの実験で試行した結果は以下の表で確認できます。

第３ブロックの実験結果 (半折り重ね)

Std	Blk	A: Seat	B: Tires psi	C: Handle Bars	D: Helmet Brand	E: Gear	F: Wheel covers	G: Gener-ator	Time 1/4 mile secs
17	3	Up	50	Up	Windy	Low	Off	Off	98
18	3	Down	40	Up	Windy	High	On	Off	88
19	3	Up	50	Down	Windy	High	On	On	61
20	3	Down	40	Down	Windy	Low	Off	On	92
21	3	Up	40	Down	Windy	Low	On	Off	91
22	3	Down	50	Down	Windy	High	Off	Off	60
23	3	Up	40	Up	Windy	High	Off	On	90
24	3	Down	50	Up	Windy	Low	On	On	97

 

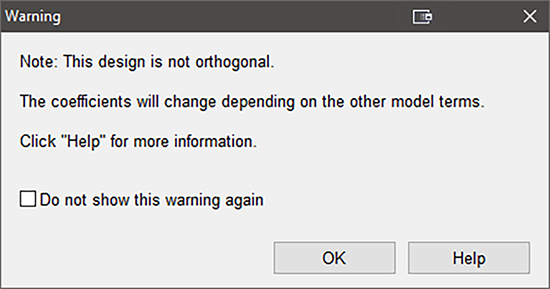
空の応答フィールドに上記と同じタイムを入力してください。入力したら、すべて正しく入力されているか、再度内容を確認してください。確認が済んだら、Analysis の “Time 1/4 Mile” ノードに移動して、“Effects” ボタンをクリックしてください。この計画が直交（orthogonal）でないことを警告する以下のダイアログが表示されます（前に少し説明したものです）。

半折り重ねが直交でないことを警告するダイアログ

 

“OK” を押したら、最大効果を右から順番に３つクリックしてください（以下の図のようにマウスで範囲を選択しても同じです）。有意となるのは B、E、および、交互作用 BE であることが分かるはずです。

 

半折り重ね後の半正規プロット

 

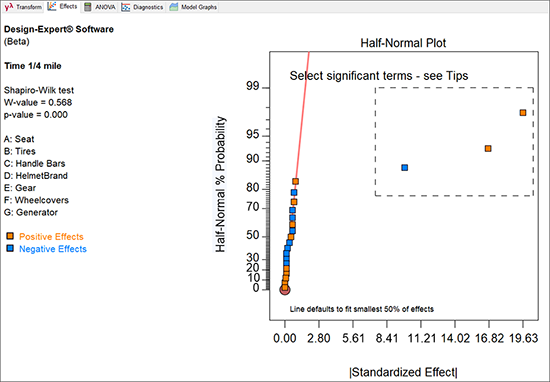再計算による効果の変化は非常にわずかに過ぎないので、その変化を見落としてしまうかも知れません。

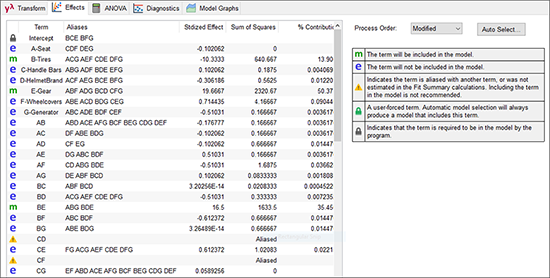
“ANOVA” をクリックすると、“This design contains aliased terms”（この計画にはエイリアス項が含まれています）という警告ダイアログが再び表示されます。“Yes” をクリックして、エイリアスのリストを表示させてください。結果は前回よりも遥かに良好です：モデル（M）項は、この応答に影響を及ぼすことが殆どありそうにない高次の交互作用のみでエイリアス化されています。

ソフトウェアによって提示されたエイリアス一覧

 

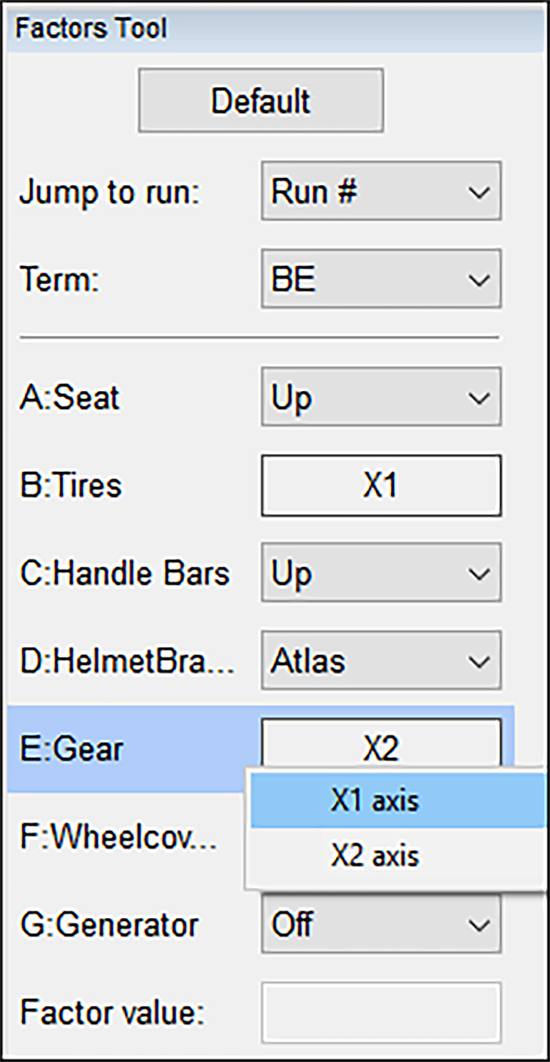
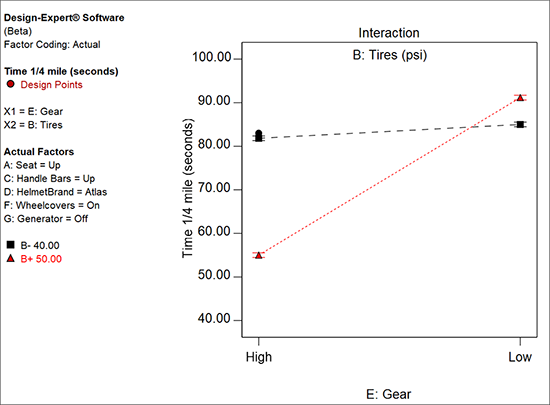
もう一度 “ANOVA” をクリックして内容を確認したら、“Diagnostics” に移動してすべてのグラフを調べてください。次に、 “Model Graphs” をクリックします。交互作用 BE のプロットの見た目は前回と同様です。実際に確認してみてください。次に、少し視点を変えて物事を見ることにしましょう。Factors Tool の “E: Gear” を右クリックして、これを “X1 axis” に指定してください。BE ではなく EB のプロットが表示されるはずです。別の言葉で言い換えれば、軸が反転したということです。グラフの直線が点線になっている点に注目してください。Gear がカテゴリ型因子（High または Low）であることをこれであらわしているのです。前の BE プロットにおいては、B（タイヤ圧）が高低両極の間の任意の水準に適合できる数値型因子であったため、その直線は実線であらわされていました。

E：GearにX1 axisを設定

 

X1軸にGearを選択した交互作用BEのプロット