
信頼に応える確かな統計
SYSTAT(シスタット) は、基本統計から複雑な多変量解析まであらゆる統計手法をカバーする統計解析ソフトウェアです。実験計画法、多変量分散分析、因子分析 (主成分分析を含む)、判別分析、クラスター分析、時系列分析など様々な多変量解析に対応し、サイエンスデータ、エンジニアリングデータをより早くより正確に解析することができます。
広範な用途に適応する包括的な統計手法を装備
- 度数分析から因子分析まで、平均から混合モデルまで、相関関係からコレスポンデンス解析まで、 あらゆる用途に対応
- 線形、一般線形、混合線形モデルにもとづく一変量および多変量データの包括的な解析
- グラフを自動的に出力する Quick Graphs 機能を使って解析結果を直感的で迅速にフィードバック
- SYSTAT の仮説チェック機能を使った解析結果の品質向上
統計データや解析結果を表現する他に類を見ないグラフィクス機能
- SYSTAT に用意された学術向けグラフタイプを活用すれば、目的に適ったグラフを作成できます。Interactive Graphics Dialog の統一されたダイアログ画面を使って様々な角度からグラフを表現できます。サブグループ間の比較、チャートの重ね合わせ、座標の変換、地図の追加、色やシンボルの変更など、洞察力に富んだプレゼンテーションの作成が可能です。グラフの配置を変更し、ポイント&クリックするだけで軸ラベルやスケール、色、シンボルを変更できます。
- 正規およびカーネル密度、マルチプロット、マップ、ボロノイ分割、関数プロット、等高線図、20種の対角密度を選択できる散布図行列、126種のノンパラメトリックスムージングオプションなど、高度なチャートオプションで統計データに含まれる重要な特徴を引き出すユニークなグラフを作成できます。
作業にあわせて自由にカスタマイズできるインターフェース
- 「スタートページ」から、前回使用した複数のデータセット、コマンドスクリプト、アウトプットおよび PDF マニュアルに簡単にアクセスすることができます。SYSTAT の豊富なワークスペース用テーマを使えば、作業やスタイルにあわせてメニューやツールバーを自由にカスタマイズすることができます。
開発元:Grafiti LLC
機能一覧
SYSTAT 製品概要
- SYSTAT は、デスクトップ環境で専門的な統計分析を実現させる多数のグラフタイプとオプションを装備しています。マップ、マルチプロット、カーネル密度といった高度なグラフタイプを使えば、洞察力のあるプレゼンテーションを作成できます。SYSTAT のインタラクティブなグラフィックツールを使えば、分析にかかる時間を大幅に縮減できます。グラフの概観をカスタマイズする際も、すべての操作はポイントアンドクリックのみで設定することができます。
- SYSTAT の直感的な Windows インターフェースとフレキシブルなコマンド言語は、あなたの研究をより一層効率化できるよう設計されています。高度なオプションも明瞭で包括的なダイアログを通じて素早く取り出して利用できます。コマンドを通じた双方向的な分析を行うこともできます。SYSTAT の クイックグラフ機能を使えば、あなたの研究結果を直ちに可視化することができます。
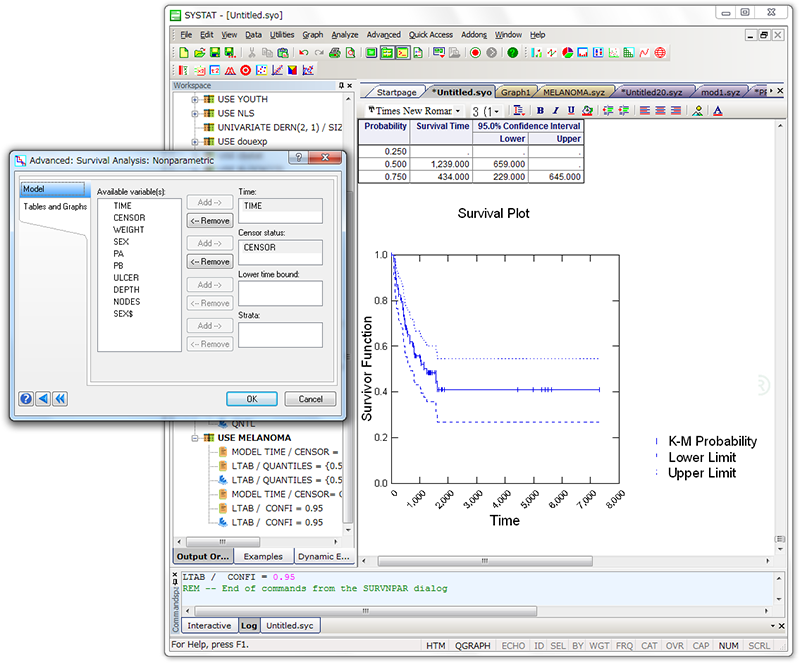
一般機能
SYSTAT は、グラフィカルな環境で使用する、わかりやすいメニューと簡潔なダイアログ ボックスを備えた、統計・グラフ解析システムです。 ほとんどの作業を、マウスでポイントクリックするだけで実行することができます。
- アウトプット、データおよびグラフエディタウィンドウがタブで仕切られたひとつのウィンドウに統合。
- メインメニュおよび右クリックメニュをカスタマイズ可能。
- ドラッグ&ドロップおよび右クリックメニューの機能の拡張
- 処理速度の向上
使いやすさと、リファレンスおよび分析
- カスタマイズ可能なツールバー
- ダイアログを通じたファイルパスの設定
- ツールバーを通じたグローバルオプションの設定
- マニュアル(PDF):Getting Started, Statistics I, Statistics II, Statistics III, Statistics IV, Graphics, Data, Language Reference, Monte Calro, Quality Analysis, Exact Tests (※いずれも英語マニュアルです)
- 500 を超えるコマンドファイル例題集
- 充実したオンラインヘルプシステム
- 統計用語集
自動化
- メニュー機能を完全にカバー
- インタラクティブなコマンド入力と解析
- コマンドファイルによる繰り返し処理の自動化
- コマンドログによるセッション履歴を保存
- コマンドテンプレートの作成を支援するトークン
- 500種を超えるコマンドファイルの例題集。類似の分析を行う際に再利用可能。
データ管理機能
- 32,000 個までの変数と、無制限の行数を使用可能。
- Mersenne-Twister 法またはWichmann-Hill 法による乱数の生成
- 行列計算– メニューにより実行可能。
- 変数の計算:数学演算子、関係演算子、論理演算子、IF THEN コマンド、三角関数、指数関数、対数、多変量、文字、日付、時刻関数
- 異なるダイアログボックスにおけるドラッグ&ドロップ、右クリックメニュによる変数の選択。
- Stata、Statistica、JMP、Minitab、S-Plus 等のデータファイルの読み込み。
- すべてのダイアログボックスの入力フィールドにおけるツールチップ形式での値の範囲表示。
- ダイアログボックスおよびデータビューにおける数値、文字、日付型フィールド別のアイコン表示
- 制限されたパラメータの入力項目をもつダイアログボックスにおける複数入力。入力はユーザーによって追加・削除可能。
- 変数のランクおよび標準化
- 欠損値の取扱い
- カテゴリのラベル付けおよび並び替え
- データのソート、変換:ファイルのマージまたは付加
- 一時データセットの作成
- ASCII (*.dat, *.txt)、Excel 2007 以前 (*.xls, *.xlsx)、SAS (*.sd2, *.xpt, *.tpt)、SPSS (*.sav)、BMDP (*.sav, *.por)、dBASE (*.dbf)、ODBC 、ArcView (*.shp) などのファイル形式を使用可能
- 選択したケース(行)や特定変数の保存
- データ操作のための BASIC: read、select、sort、transform、print、save、無作為標本の生成、その他
アウトプットオーガナイザ
- 出力や操作を容易にするナビゲータによる指示
- グラフを組み合わせた統計レポートの出力
- 統計出力の短形式、中形式、長形式アウトプット
- ヘッダ、フッタ、ページ設定、プリントプレビュー
- RTF、HTML 形式での保存
(グラフは、BMP、WMF、EMF、PCT、EPS、JPG、CGM ファイルに保存可能)
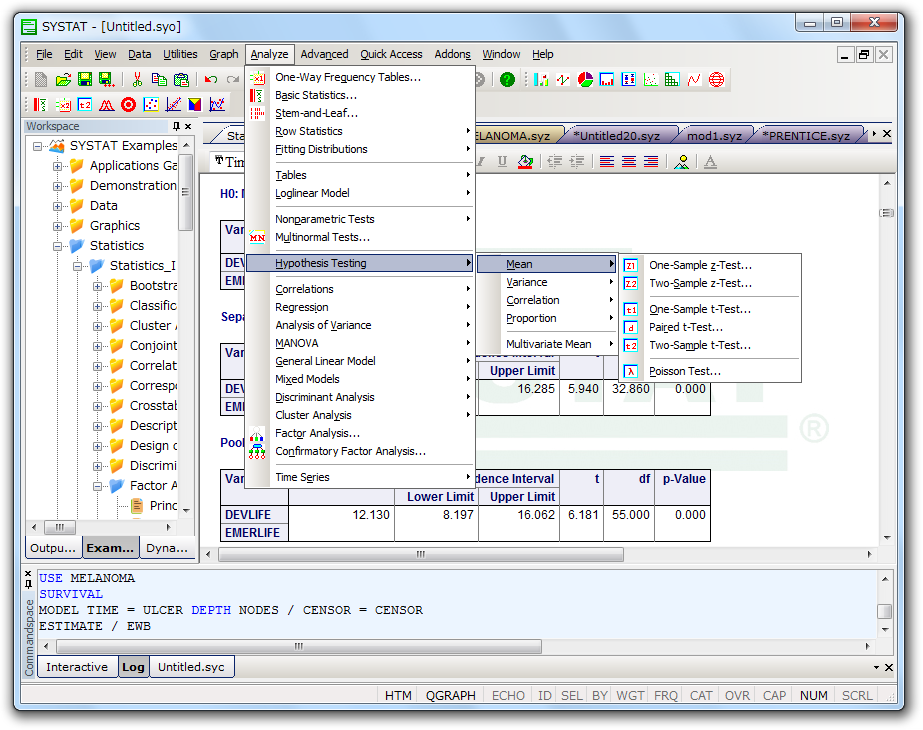
統計解析機能
SYSTAT を使えば特別な調査データに対する正しい統計手法を見つけるのに悩まされることはありません。
統計解析の専門家によるアルゴリズムは、例えデータがどんなに極端なものでも信頼性の高い結果をもたらします。
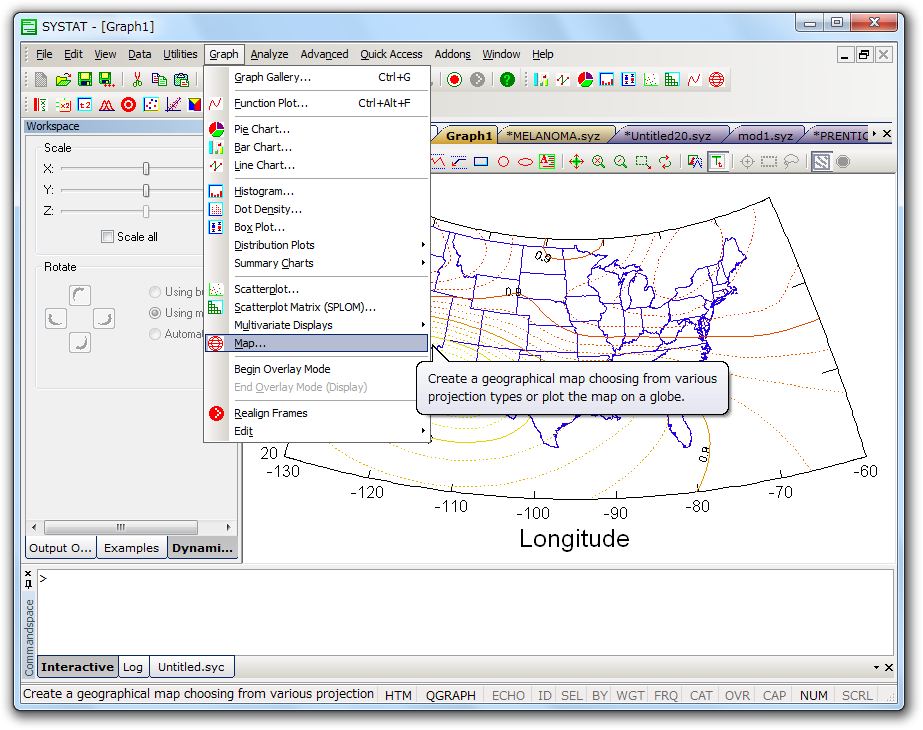
グラフ機能
SYSTAT では無制限にグラフを重ね合わせることができ、ページビューやオブジェクト、注釈の描画も可能です。グラフの位置、スケール、軸ラベル、タイトル、カラー、シンボル等がポイント&クリックで容易に編集できます。
活用例
SYSTAT には、様々な分野のアプリケーションが用意されています。これらのアプリケーションはオンライン ヘルプに収録されています。 ヘルプシステムの「目次」タブを使用して「応用例ギャラリー」にアクセスしてください。 解析の例が、必要なコマンドおよびメニューとともに表示されます。必要なデータ ファイルおよびコマンド ファイルもすべて用意されています。
SYSTAT グラフギャラリー
アップデート情報
各アップデート情報は こちら をご確認ください
動作環境
SYSTAT 13 動作環境
Windows XP, Windows 7, 8.x, 10 & Windows Vista
- プロセッサ :1 GHz の 32-bit (x86) または 64-bit (x64) プロセッサ
- システムメモリ 32-bit (x86):1GB
- システムメモリ 64-bit (x64):2GB
- ハードディスク空き容量: 100 MB
- 800×600 SVGA/256 色以上のディスプレイ
- Internet Explorer 8 以降
- 英語版・英語 PDF マニュアル付き
- マニュアル(PDF):Getting Started, Statistics I, Statistics II, Statistics III, Statistics IV, Graphics, Data, Language Reference, Monte Calro, Quality Analysis, Exact Tests (※いずれも英語マニュアルです。)
| ※ Standalone ライセンス(通常のライセンス)は、Windows のターミナルサービス (含:リモートデスクトップ)を介して、使用することはできません。この場合、同時使用ユーザライセンス(SIMUS)をご利用いただく必要がございます。同時使用 ユーザライセンスに関しては、ライセンスの項目をご覧ください。 |
| ※ 英語アプリケーションのため、使用できるテキストデータはアルファベットのみとなります。日本語 (2バイトコード) には対応しておりません。 |
ライセンス
SYSTAT ライセンスプログラム
| ライセンス形態 | シングルユーザー ライセンス |
Site ライセンス | SIMUS ライセンス | ||
| ライセンス型 | Perpetual | Perpetual | Annual | Perpetual | Annual |
| 期限 | 無期限 | 無期限 | 1 年間 | 無期限 | 1 年間 |
シングルユーザーライセンス
- 使用権
1 名 (登録ユーザのみ) - インストール可能台数
2 台まで
※ 2 台同時に使用することはできません。 - プロダクトキー/ライセンスファイル
1 つのシリアルナンバーに対してプロダクトキーが 1 つ発行されます。1 つのプロダクトキーで 2 台の PC をアクティベートできます。
プロダクトキーでアクティベートできない場合や、インストールした PC を変更する場合は、PC 毎にライセンスファイルの取得が必要です。
Site (サイト) ライセンス
- 対象
5 本以上
1 つのシリアルナンバーで複数のライセンスを管理することができます。(同時使用ライセンスではありません。) - 使用権
登録された法人/大学に所属する正社員およびパートタイム社員/正規職員およびパートタイム職員。研究室に所属する学生の使用も認められます。 - インストール可能台数
購入時に指定したライセンス数分の PC にインストール可能です。(ライセンス管理ソフトは不要です。)
| ・ シリアル番号が同じライセンスは同じ Site (敷地) 内の PC にインストールします。 ・ インストールする PC は、ご注文時に「ユーザー情報確認書」 ( ・ ユーザー情報確認書にご記入されたユーザ様がサイトライセンス担当者として登録されます。 |
- プロダクトキー/ライセンスファイル
- 1 つのシリアルナンバーに対してプロダクトキーが 1 つ発行されます。1 つのプロダクトキーでライセンス数分の PC をアクティベートできます。
プロダクトキーでアクティベートできない場合や、インストールした PC を変更する場合は、PC 毎にライセンスファイルの取得が必要です。
※ Site ライセンスの PC 変更用のライセンスファイルは、メンテナンスが有効な場合のみ申請できます。
SIMUS (サイマス:同時使用) ネットワークライセンス
- 対象
5 ユーザ以上
使用時には、ネットワークサーバーへのアクセスが必要です。 - 使用権
登録された法人/大学に所属する正社員およびパートタイム社員/正規職員およびパートタイム職員。
研究室に所属する学生の使用も認められます。 - インストール可能台数
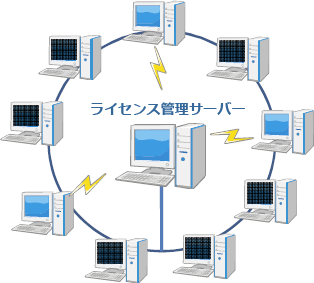
ライセンス管理サーバ 1 台にインストールし、
任意数のクライアント PC にインストールすることができます。
同時に使用できるユーザ数は、購入時に指定した数です。
| ・ インストールする サーバー/PC は、ご注文時に「ユーザー情報確認書」 ( ・ ユーザー情報確認書にご記入されたユーザ様が SIMUS ライセンス担当者として登録されます。 |
- プロダクトキー/ライセンスファイル
1 つのシリアルナンバーに対してライセンス管理サーバー用のプロダクトキーが 1 つ発行されます。
プロダクトキーでアクティベートできない場合や、サーバーを変更する場合は、ライセンスファイルの取得が必要です。
※ SIMUS ライセンスのサーバー変更用のライセンスファイルは、メンテナンスが有効な場合のみ申請できます。
プロダクトキーとライセンスファイル申請
- プロダクトキー
ご購入時にライセンス毎に発行されます。プロダクトキーを使ってデモ版から製品版にアクティベートできます。 - ライセンスファイル
ご使用されるマシンで生成された C2V ファイルを元に開発元より発行されます。 ネットワーク環境にない等の理由でプロダクトキーでアクティベートできない場合や、プロダクトキーでアクティベートした後にマシン変更をする場合は、下記の専用フォームよりライセンスファイルを申請してください。 - Grafiti 社製品ライセンスファイル申請フォーム
トライアル
デモ版お申込み
製品版のすべての機能をインストール後 30 日間ご利用いただけます。
デモ版は一つのマシンで 1 回限り導入できます。
製品価格
製品名 | 税込価格 |
|---|---|
| SYSTAT 13.2 シングルユーザライセンス 一般用 | ¥217,800 |
| SYSTAT 13.2 シングルユーザライセンス 官公庁用 | ¥171,600 |
| SYSTAT 13.2 教育用 シングルユーザライセンス | ¥111,100 |
● 製品はダウンロード提供です。
● ご購入の際は、エンドユーザー様の「ユーザー情報確認書」 ( ![]() PDF /
PDF / ![]() Excel ) が必要です。
Excel ) が必要です。
ライセンス
SYSTAT には、シングルユーザーライセンス / Site ライセンス / SIMUS ネットワークライセンスがあります。
- シングルユーザー (無期限のみ)
- Site 5L ~ (無期限 または 年間)
- SIMUS ネットワーク 5-user ~ (無期限 または 年間)
各ライセンスの使用権やインストール可能台数等については、SYSTAT ライセンスプログラム をご覧ください。
- 官公庁用
政府、地方自治体が運営する法人、組織が対象となります。独立行政法人も含まれます。
(第三セクターは対象外となります。) - 教育用
学位授与機関、および、そこに所属し教育・研究目的でご購入される方が対象となります。
プロダクトキー / ライセンスファイル
ご購入時に、1 つのシリアルナンバーに対してプロダクトキーが 1 つ発行されます。
プロダクトキーでアクティベートできない場合や、マシン変更の際には、ライセンスファイルを取得する必要があります。 ライセンスファイルは、Grafiti 社製品ライセンスファイル申請フォーム よりお申し込みください。
メンテナンス
Site / SIMUS ネットワークの無期限ライセンスには、メンテナンス (年間保守) を付けることができます。メンテナンスの有効期間中に提供されるサービスには、以下が含まれます。
- 最新バージョンのアップデートとアップグレード
- マシンを変更するためのライセンスファイル再発行
お見積り・ご購入
製品補足情報欄に、ご希望のライセンスタイプ (シングルユーザー / Site / SIMUS ネットワーク) をご記入ください。 Site / SIMUS ライセンスの場合は、期間 (年間 / 無期限)、ユーザー数もお知らせください。
アップグレード
※ アップグレード価格は、上記のお見積りフォームよりお問合せください。
- SYSTAT 13.2 へアップグレード可能なバージョン
- SYSTAT 13
- SYSTAT 12
- SYSTAT 11
- SYSTAT 10
- アップグレード後は新しいシリアル番号が付与されます。旧シリアル番号のサポート (ライセンスファイル再発行を含む) は終了します。
- 現在お持ちの製品名、バージョン、シリアル又はライセンス番号を必ずご記入ください。
サポート
SYSTAT サポート情報
| ※ 現在のサポート対象バージョンは 13 と 12 です。 |
|---|
| サポートが終了しているバージョンは、ライセンスファイル再発行ができません。ご使用中のマシンでは 継続してご使用になれますが、マシン変更をされますと使用できなくなります。 |
- SYSTAT テクニカルサポート情報
インストール手順、チュートリアルはこちらをご覧ください。 - Grafiti 社製品ライセンスファイル申請フォーム
プロダクトキーでアクティベートできない場合や、マシン変更の際には、上記の専用フォームよりライセンスファイルをお申し込みください。ライセンスファイルの発行まで日数を要する場合があります。予めご了承ください。
ライセンスファイルは、お使いの PC 固有の情報を元に開発元から発行されます。申請の際にはお客さまの英文情報と、ご使用される PC で生成された C2V ファイルが必要です。
