
| ★ SigmaPlot 16 にアップグレードしよう! :バージョン16までに統計グラフ機能が段階的に追加されてきました。バージョン 14.5 で追加された ジッター プロット、v15 で追加された Dot Density プロット、v16 で追加されたヴァイオリンプロット、バタフライプロットなど、いずれも取り扱うデータの全体像を分かりやすく示すためのプロット、これらを使い分けることで目的や場面に応じた分かりやすいグラフを作成することができます。 |
| ★ SigmaPlot 統計基本操作ガイドに One-way ANOVA を追加しました。統計基本操作ガイドは こちら よりご覧ください。New! |
研究成果をこの上なき表現にまで高める分析とグラフ作成
SigmaPlot は、Windows プラットフォーム用に設計された最先端の学術向けグラフ作成プログラム です。研究結果のグラフ表現を専門とするソフトウェアで、特に論文の作成や出版の支援を目的に設計されています。
出版品質の明瞭なグラフ、データ分析、プレゼンテーションのための豊富なツールが装備されており、研究成果の的確な表現を容易に行うことができます。自動エラーバー、回帰直線、信頼区間、軸の中断、特殊な軸スケール、非線形カーブフィッティングといった科学技術に特化した専門的な多彩なオプションと、パワフルなデータ操作を可能にするワークシートが用意されています。
● グラフの作成と編集
Create Graph タブをクリックして、グラフの種類を選択したら、表示される Graph Wizard で使用するデータをマウスで選択すると、即座にグラフが作成されます。ワークシートの書式を設定したり、テンプレートや Graph Style Gallery を使用してお気に入りのグラフを繰り返し作成することもできます。
グラフタイプ:作成するグラフの骨格を決定するものです。SigmaPlot には、パイチャートや極座標プロットはもちろん、2 次元および 3 次元の直交座標系 (XY および XYZ) グラフのタイプが数多く用意されています。
グラフスタイル:グラフ上にデータをプロットする方法を決定するものです。選択できるスタイルは、グラフタイプによって変わります。Graph Wizard を使えば、各グラフタイプに関連付けられた利用可能なグラフスタイルの一覧を簡単に表示させることができます。
グラフスタイルギャラリー:グラフスタイルがそれぞれサムネイルのプレビューとして表示されます。このウィンドウから好みに合うスタイルを選んで新規グラフを作成することができます。グラフスタイルは、新規に作成することも、予め用意された豊富なテンプレートの中から好きなものを選んで利用することもできます。
テンプレート:SigmaPlot のテンプレートノートブックにはさまざまなページレイアウトが用意されています。あらかじめ定義されているこれらのテンプレートの属性を既存のページやグラフに適用したり、新たに定義したテンプレートを作成することができます。
● ワークシート
最大 32,000,000 行、32,000 列までのデータをワークシートで取り扱うことができます。データを複数列または複数行に入力すると、行方向または列方向のいずれの方向でも計算を実行することができます。
ワークシートの列内のセルは調整可能で、有効数字 16 桁まで格納することができます。グラフに加える変更を指定するために、ラベルを配置したり、塗りつぶしカラーとパターンをカスタマイズしたり、エラーバーの向きを指定するコードをセルに入力できます。
● データ解析
非線形回帰 [カーブフィット機能]
回帰分析 (Regression) は、一般に科学者や技術者が実験データの状態や特性をあらわすのに最適な曲線としてプロットするのに利用される手法です。SigmaPlot では、回帰ウィザード (Regression Wizard) を使って回帰分析およびカーブフィッティングを行います。回帰ウィザードでは、曲線のあてはめ、プロット作成、レポートの生成といった一連の手順を進行します。
カーブフィット機能は、方程式のパラメータ (係数) を変化させることによって、実験データに最も近似するような方程式のパラメータを求めるものです。方程式のパラメータは最大 25 まで、独立変数は最大 10 まで指定できます。また、カーブフィットでパラメータ値を求める際にその探索範囲を制限するためにパラメータの制約条件を最大 25 まで指定することができます。回帰曲線のあてはめ機能では、重み付き最小二乗法 (weighted least squares) を使用して精度を向上させることも可能です。
統計解析機能
SigmaPlot の Analysis タブには SigmaStat が用意されています。適切な検定法の選択までに至るプロセスをガイドする Advisor Wizard を含む、データ分析によく利用される統計検定が 50 種類装備されています。統計結果に関しては、詳細なレポートが読みやすい形式で出力され、その多くは結果に関する解釈が付けられます。また、統計結果のグラフも出力されます。
記述統計 (Descriptive statistics) は、ワークシートのすべての列で利用できます。Statistics Worksheet には、ワークシートのすべての列に関する基本統計量が一覧で表示されます。
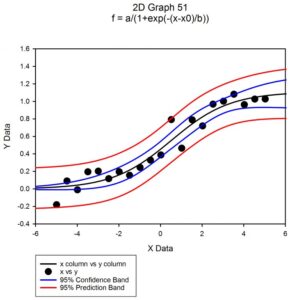
線形回帰直線を信頼区間および予測区間付きで表示したり、グラフに列平均のエラーバーを描画したり、ワークシートの列間で対応のある t 検定や対応のない t 検定を実行できます。ヒストグラム機能を使用すれば、データセットの分布を計算しプロットすることができます。
● モジュール機能
Enzyme Kinetics Module (酵素反応速度分析モジュール)
素早く簡単に、酵素反応速度論データを分析し、グラフを作成することができます。
Pharmacology Module (薬理学用モジュール)
探索的酵素反応速度論 (Exploratory EK)、保管寿命 (shelf life) の決定、簡易リガンド結合 (simple ligand binding) 計算、検量線 (standard curve) 分析を実行することができます。
開発元:Grafiti LLC
機能一覧
SigmaPlot 製品概要
グラフタイプ
- ヒートマップ (マクロ)
- Q-Q (Quantile-Quantile) プロット
- 信頼楕円および予測性楕円
- ジッタープロット
- フォレストプロット / フォレストグラフ
- カーネル密度プロット
- 平均値と信頼区間付きドット密度
- レーダープロット
- ドット密度グラフ
- 2D ベクトルプロット
- 3D 等高線投影付きメッシュプロット
- ワイブル軸スケールによるワイブル分布のプロット
- 極座標プロットの正方向を選択
- 逆数(アレニウス)スケールの作成
- 面プロット – 交点
- 面プロット – 曲線の下に陰影
- 2D/3D 関数プロッタ
- 2D 塗りつぶし等高線
- ウォーターフォール / ローソク足
- 三角プロット / 3D メッシュ
グラフ編集
- 結果グラフのデフォルト外観の改善
- 直線、楕円、ボックス、矢印を描画
- Anti-Aliasing ボタン (Graph Page タブ > Format Group)
- 10 種類のカラースキーム
- 横型、縦型、長方形の凡例形状
- 凡例アイテムの並べ替え
- ミニツールバーによる凡例アイテムの編集
- プロットの横に凡例テキストを配置するダイレクトラベリング
- 凡例タイトルの追加
- 凡例アイテムの反転
- マウスによる凡例アイテムとボックスの編集
- ズーム、パン、ドラッグ操作
- マウスホイールスクロールの有効化
- カラーグラデーションと透明度
- アンチエイリアスライン
- 時系列でのスクロール機能
- 3D グラフのカスタマイズ
- 多数の線種と塗りつぶしパターン
- 不規則な間隔の 3D データを自動でグラフ化
- グラフグループの自動サイズ変更と位置決め
- 選択可能なグラフオブジェクトとグラフデフォルト
- カーブフィットの信頼帯を自動生成
- 2D/3D 等高線プロットのための軸スケール
- 30 種類以上のシンボル形状
- カテゴリーグラフのサポート – データの再フォーマットを回避
- Microsoft Equation Editor サポート
- 個々のオブジェクトの選択と編集 – 線、棒
- 複数のオブジェクトの選択と編集
- ページ上でのインプレーステキスト編集
- 凡例 – グラフまたはデータへの自動ロック
- グラフページのルーラーの調整
- グリッドへのスナップ
- 透明な 3D メッシュ
- 3D メッシュの塗りつぶしのスムース化とグラデーション
ユーザーインターフェース
- VS 2008 スタイルのリボンマネージャー
- ホームボタンアイコン
- リボンアイコン
- Macros タブ
- マクロのリボンタブをハイライト表示
- Help リボンタブ
- リボンメニュー機能 (クイックアクセスツールバーに設置)
- スタートアップ画面 (4K 問題修正済)
- Analysis タブの Histograms グループ
- ワークシート、グラフ、レポートにおける Unicode 文字と記号のサポート
- プログラム選択により変化するリボンインターフェース
- グラフ、統計、マクロ、トランスフォーム、非線形回帰のサンプルファイルをヘルプに掲載
- 変換および「列から選択」によるデータ依存のカラーグラデーション、シンボル、サイズを作成
- ノートブック項目をドラッグして並べ替え
- SigmaPlot チュートリアル (PDF)
- Microsoft Office スタイルのリボンコントロール
- オブジェクトブラウザとプロパティブラウザ
- プロパティ変更時の即時動的グラフ更新
- プロパティグループスタイルのコピー&ペースト
- タブ付きウィンドウインターフェイス
- ドッキングパネルガイド
- 垂直および水平タブグループ化
- オブジェクト固有のミニツールバー
- カスタマイズ可能なクイックアクセスツールバー
- 書式設定済みワークシート
- マウスオーバー時のリアルタイム座標フィードバック
- プログラム起動ウィザード
- Submission Assistant
- カスタマイズ可能な Transform ライブラリ
- 監査証跡 – ノートブックとログイン名への変更を追跡
- パスワードで保護されたノートブック
- ブラウザスタイルのノートブックマネージャ
- ワンステップマルチセルフォーマット
- 行と列のタイトルの複製が可能
- 印刷プレビュー
- ペインのフリーズ、検索と置換
- Microsoft Excel の矢印の動作
- ワークシートセルのテキストラップ
- 編集可能な日付と時刻の書式
- Quick Transform で使用する数式を列タイトルに表示
- 複数回の取り消し
- 自動保存
- グラフスタイルギャラリー
- 1 ページに複数のグラフを配置可能なテンプレート
- グラフページのルーラーと調整可能な Snap-to-Grid
- カスタムズーム
- ノートブックでのレポート編集
データ解析
- Result Graph データを統計レポートと共に保存
- [オプション] ストレージの容量に問題がある場合、Result Graph データをレポートと共に保存しない (デフォルトではオン)
- Run ボタンをクリックした後も User Defined Transforms ダイアログを表示
- [オプション] Run ボタンを押した後に UDT ダイアログを解除する (デフォルトではオン)
- 回帰ウィザード:150 以上のグラフィカルな方程式
- 最大 50 の独立変数と 500 のパラメータを持つレーベンバーグ・マルカート法
- 回帰統計の自動プロット
- 列記述統計の自動生成 – 選択と順序の指定
- One-Way Frequency Tables
- 非等分散を仮定するウェルチの T-検定
- 統計学による結果グラフ
- 主成分分析 (PCA)
- 共分散分析 (ANCOVA)
- ノンパラメトリック P 値の解析的計算
- 赤池情報量規準 (AICc)
- カーブフィットライブラリ “standard.jfl” に含まれる 24 個の確率関数
- 各カーブフィットファイルに 7 個の重み付け関数が付属
- Enzyme Kinetics Module (酵素反応速度分析モジュール)
- 予測値を用いた重み付け方法とロバスト回帰のための重み付け方法
- レポートにおけるパラメータの共分散行列と信頼区間
- 陰関数カーブフィッティング
- ノンパラメトリックな 1 標本の T-検定
- X と Y の両方で誤差を許容するデミング回帰
- 品質管理のための正規分布の比較
- 平行線分析
- Bland-Altman 法で測定方法を比較
- Dunnett 検定と改良型 3 元配置分散分析 (Three Way ANOVA) における P 値の改善
- Transform 言語によるワークシートの行と列のタイトル付け
- Transform 言語の新関数 Root() と Implicit()
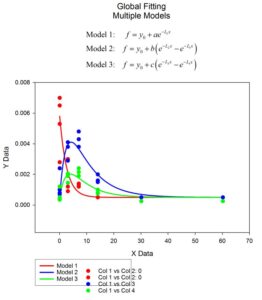
- グローバルカーブフィッティング
- 完全なアドバイザリー統計解析
- Standard Curves マクロ
- Dynamic Fit ウィザード – グローバルミニマムの検索
- ROC 曲線解析
- 24 の確率変換関数
- 区分線形回帰 – 2, 3, 4, 5 セグメントモデル
- 非線形カーブフィッティングの追加統計結果
- 複数行の方程式
- ある範囲の値に対して同時に解く
- リガンド結合解析
- 数学的方程式を評価する方程式ソルバー
- 2D データ用の 6 つのスムージングルーチン
- 3D データ用の 7 つのスムージングルーチン
- ポイントアンドクリックでデータ変換する Quick Transforms
- ヒストグラムウィザード
- カーブフィッティングのための回帰ウィザード
- サマリー統計
インポート / エクスポート
- SVG と SWF スケーラブルグラフィックスをベクトルファイルフォーマットでエクスポート
- ベクトル PDF エクスポート
- Minitab, SAS, SPSS ファイルのインポート / エクスポート
- PDF エクスポート
- EMF ファイルのサポート
- SAS および Minitab データファイルのインポート
- グラフページでのグラフィックファイルの直接インポート: BMP, JPEG, GIF, TIFF その他多数
- ODBC インポート
- グラフ & レポートの PDF エクスポート
- レポートの HTML エクスポート
- Microsoft Access MDB データのインポート
- グラフエクスポートウィザード – DPI を計算、ページサイズ
- トゥルーカラーベクトル EPS グラフエクスポート
- 圧縮 TIFF CMYK グラフエクスポート
- WebViewer
- 24-bit カラーでのラスター EPS & CMYK グラフエクスポート
- ノートブック内の選択されたアイテムの一括印刷
- グラフィックファイルフォーマットのエクスポート: TIFF, JPG, WMF, BMP, EPS
オートメーション
- グラフページの測定単位を指定
- 自動凡例状態の指定
- Quick Transforms の自動更新
- 方程式の自動配置
- ツールボックスマクロメニュー
- カスタマイズ可能な組込みマクロ
- Visual Basic ベースのマクロ
- 組込みマクロレコーダーで操作を再生
- オートメーションオブジェクトサポート – カスタムアプリケーションへのリンク
- OLE および OLE 2 クライアント/サーバー
MS WINDOWS との連携
- CF_SYLK クリップボード形式で Excel から数値を完全精度でペースト
- [オプション] クリップボード形式 CF_UNICODETEXTに変更 (Excel から数値データを完全精度でペースト。非 ASCII 文字のペーストは不可)
- ソフトウェアアップグレード時のユーザーオプションの自動引継ぎ
- Excel ファイルを直接 SigmaPlot にインポート
- サイレントインストールのサポート能
- Network License Manager
- Microsoft Excel©, Word©, PowerPoint© のサポート
- SigmaPlot™ から Microsoft Excel を実行
エラーバー
- エラーバープロットのカテゴリーデータ (グループ)
- エラーバーと箱ひげ図におけるパーセンタイル法
- 非対称エラーバー / 反復値からのエラーバー
- エラーバーの計算 – 標準偏差、標準誤差、95% および 99%
ワークシート
- 色、パターン、シンボル、線種、目盛間隔、目盛ラベルなどをワークシートに直接入力
- ワークシートの列から線幅を指定
- ミニツールバーでワークシートセル編集
- ワークシートのズーム有効化
- ワークシートセルの書式付きテキスト
レポート
- 定義済みスタイルまたは完全カスタマイズによる表の挿入
- レポートと Excel ワークシート間で表形式データをコピー/ペースト
- レポートのズーム有効化
- グラフウィンドウに縦・横ルーラーを表示
- レポートの背景色の変更
- 最新バージョンのレポートエンジン
- Word 2007/2010 のコンテンツをレポートページに直接ドラッグ&ドロップ可能
トランスフォーム
- 数学的変換 – ユーザー定義ダイアログのサイズ変更と保存が可能
- 改良型のクイックトランスフォームダイアログのユーザーインターフェース
- プロパティブラウザのオブジェクトウィンドウにクイックトランスフォームのリストを表示
- クイックワークシートウィンドウをマウスホイールでスクロール可能
ギャラリー
動作環境
SigmaPlot 16 動作環境
ハードウェア
- CPU: 2 GHz の 32-bit (x86) または 64-bit (x64) プロセッサ
- システムメモリ
32-bit (x86):4 GB
64-bit (x64):8 GB - HDD: 1 GB
- 1366×768 以上のディスプレイ解像度
- Internet Explorer Version 8 以降
ソフトウェア
- Windows 11; Windows 10
- Microsoft Edge, Firefox, Google Chrome
- Office 2010 以降 (PowerPoint スライドへの貼り付け、Word へのグラフ挿入、その他のマクロ)
※ ソフトウェアをダウンロードするためのインターネット接続が必要です。
※ 64-bit 環境では 32-bit モードで動作します。
※ Windows のターミナルサービス (リモートデスクトップを含む) を介して使用する場合は、SIMUS (ネットワーク) ライセンスをご購入ください。シングルユーザーライセンスはご利用いただけません。
ライセンス
シングルユーザーライセンス
- 使用権
1 名 (登録ユーザーのみ) - インストール可能台数
2 台:登録ユーザーが所有または管理下にあるパーソナルコンピュータ 1 台と、登録ユーザーが所有する追加のコンピュータ 1 台
(例:自宅と職場のコンピュータ)
※ 2 台同時に使用することはできません。 - プロダクトキー/ライセンスファイル
1 つのシリアルナンバーに対してプロダクトキーが 1 つ発行されます。1 つのプロダクトキーで 2 台の PC をアクティベートできます。
プロダクトキーでアクティベートできない場合や、インストールした PC を変更する場合は、PC 毎にライセンスファイルの取得が必要です。
SIMUS ネットワークライセンス
- 対象
5 ユーザ以上
使用時には、ネットワークサーバーへのアクセスが必要です。 - 使用権
登録された法人/大学に所属する正社員およびパートタイム社員/正規職員およびパートタイム職員。研究室に所属する学生の使用も認められます。
※ ご購入時にユーザー情報確認書に記載されたユーザー様がライセンス担当者として登録されます。
- インストール可能台数
ライセンス管理サーバー 1 台にインストールし、任意数のクライアント PC にインストールすることができます。
インストールする サーバー/PC は、登録された法人/大学が所有するものに限ります。
同時に使用できるユーザー数は、購入時に指定した数までです。 - プロダクトキー/ライセンスファイル
1 つのシリアルナンバーに対してライセンス管理サーバー用のプロダクトキーが 1 つ発行されます。
プロダクトキーでアクティベートできない場合や、サーバーを変更する場合は、ライセンスファイルの取得が必要です。
Site ライセンス
- 対象
5 本以上
1 つのシリアルナンバーで、同じ Site (敷地) 内の複数のライセンスを管理することができます。(同時使用ライセンスではありません。) - 使用権
登録された法人/大学に所属する正社員およびパートタイム社員/正規職員およびパートタイム職員。研究室に所属する学生の使用も認められます。
※ ご購入時にユーザー情報確認書に記載されたユーザー様がライセンス担当者として登録されます。 - インストール可能台数
購入時に指定したライセンス数分の、同じ Site (敷地) 内にある PC にインストール可能です。(ライセンス管理ソフトは不要です。)
インストールする PC は、登録された法人/大学が所有するものに限ります。 - プロダクトキー/ライセンスファイル
1 つのシリアルナンバーに対してプロダクトキーが 1 つ発行されます。1 つのプロダクトキーでライセンス数分の PC をアクティベートできます。
プロダクトキーでアクティベートできない場合や、インストールした PC を変更する場合は、PC 毎にライセンスファイルの取得が必要です。
プロダクトキーとライセンスファイル申請
- プロダクトキー
ご購入時にライセンス毎に発行されます。プロダクトキーを使ってデモ版から製品版にアクティベートできます。 - ライセンスファイル
ご使用されるマシンで生成された C2V ファイルを元に開発元より発行されます。 ネットワーク環境にない等の理由でプロダクトキーでアクティベートできない場合や、プロダクトキーでアクティベートした後にマシン変更をする場合は、Grafiti 社製品ライセンスファイル申請フォーム よりライセンスファイルを申請してください。
トライアル
デモ版お申込み
製品版のすべての機能をインストール後 30 日間ご利用いただけます。
デモ版は一つのマシンで 1 回限り導入できます。
製品価格
※ 製品価格は、下記の見積依頼フォームよりお問合せください。
新規ご購入
製品補足情報欄に、ご希望のライセンスタイプ (シングルユーザー / Site / SIMUS ネットワーク) をご記入ください。
Site および SIMUS ネットワークライセンスの場合は、期間 (年間 / 無期限) とユーザー数もお知らせください。
- シングルユーザー (無期限のみ)
- Site 5L ~ (無期限 または 年間)
- SIMUS ネットワーク 5-user ~ (無期限 または 年間)
Site および SIMUS ネットワークの無期限ライセンスには、メンテナンス (年間保守) を付けることができます。メンテナンスの有効期間中、最新バージョンのアップデートとアップグレードが提供されます。ライセンスのご購入後にメンテナンスを追加することはできません。
| Windows のターミナルサービス (リモートデスクトップを含む) を介して使用する場合は、SIMUS ネットワークラセンスをご購入ください。シングルユーザーライセンスはご利用いただけません。 |
アップグレード
製品補足情報欄には現在お持ちの製品情報 (バージョン、シリアル番号) を必ずご記入ください。
アップグレード後は新しいシリアル番号が付与されます。旧シリアル番号のサポート (ライセンスファイル再発行を含む) は終了します。
| マイクロソフトの Windows 10 のサポート終了に伴い、以前の Windows オペレーティングシステム向けに設計された旧バージョンの SigmaPlot は、公式サポートの対象外となります。2025 年 10 月 15 日以降、SigmaPlot v15 以前のバージョンに対する技術サポートやセキュリティ更新プログラムは提供されません。現在お使いのバージョンは引き続きご利用いただけますが、セキュリティ上の脆弱性に晒される可能性がある点にご留意ください。 データ分析を中断なく継続するため、SigmaPlot v16 へのアップグレードを強く推奨します。SigmaPlot 16 は、Microsoft が継続サポートするオペレーティングシステムである Windows 11 上でシームレスに動作することが完全に認証・テストされた唯一の SigmaPlot バージョンです。 |
お見積り・ご購入
サポート
SigmaPlot TIPS
SigmaPlot 統計基本操作ガイド
SigmaPlot における Unicode のサポートについて
SigmaPlot では、各種インターフェースで Unicode キャラクタがサポートされますが、一定の制限があります。
インストールガイド
SigmaPlot 16
- シングルユーザーのインストール手順 (PDF)
- SIMUS (ネットワーク) ライセンスのインストール手順 (PDF)
- SigmaPlot 16 Network ライセンスのファイアウォール設定手順
- Grafiti 社製品ライセンスファイル申請フォーム
プロダクトキーでアクティベートできない場合や、マシン変更の際には、上記の専用フォームよりライセンスファイルをお申し込みください。
ライセンスファイルは、お使いの PC 固有の情報を元に開発元から発行されます。申請の際にはお客さまの英文情報と、ご使用される PC で生成された C2V ファイルが必要です。
ライセンスファイルの発行まで日数を要する場合があります。予めご了承ください。
SigmaPlot 15
- シングルユーザーのインストール手順 (PDF)
- SIMUS (ネットワーク) ライセンスのインストール手順 (PDF)
SigmaPlot 14.5
- シングルユーザーのインストール手順 (PDF)
- SIMUS (ネットワーク) ライセンスのインストール手順 (PDF)
SigmaPlot 14
サポートお問い合わせ
導入事例
● 福井大学 大学院 工学研究科 生物応用化学専攻 櫻井 明彦 教授
『酵素反応の解析では、Enzyme Kinetics Module がとても役立ちます。解析パターンがいくつもあるところも魅力の 1 つです。』
● 同志社女子大学 薬学部 薬理学教室 藤井 健志 准教授
『グラフ作成のワークシートをそのまま統計解析のデータとして扱うことができるので重宝しています。』
● 金沢工業大学 人間情報システム研究所 長尾隆司 教授
『グラフを作る上で必要なあらゆる要素を自在に扱えることが、やめられない最大の理由です。』
● 東京医科歯科大学 大学院 医歯学総合研究科 柳下正樹 教授
『自分で思った通りのグラフが作成できるわけですから、SigmaPlot は大変な福音となりました。』
